Why STEM Is Important for Any Data Scientist

3 cases to prove this from my own experience

Foreword

Once upon a time I used to study Petroleum Engineering. Honestly, I was enrolled in a bachelor’s degree almost by accident. At school I liked Physics and Math, thus I definitely wanted to study STEM at the university. At that time, I didn’t know anything about the petroleum industry and, like many other people, I thought that oil was extracted from underground lakes. But because I was successfully accepted to this program I decided to try.

I cannot say that I regret of my choice, although I must admit that I haven’t worked in the industry, except the time when I was an intern. But what I got is the scientific approach to solving various tasks, and undoubtedly this is a great gift.

In this post I want to emphasize the importance of knowing the scientific principles and laws. In most cases, they were formulated based on cumulative experience and long-term observations, and therefore have a high variety of applications in very different aspects of human lives. Data Science is not an exception, and even if not applying this accumulated wisdom directly, having an analogy with major scientific methods helps me to solve the challenging data-related tasks in a more effective way.

Case # 1: Decomposition and the Fourier transform

The Fourier transform is a method of decomposing complicated waves or signals into a set of unique sinusoidal components. This decomposition allows us to examine, amplify, attenuate or delete each sinusoidal element.

This is a formal definition of the Fourier transform, from which it is clear that the method is all about decomposition of waves in order to simplify their analysis. Therefore, the Fourier transform is useful in many applications. For instance, music recognition services use the Fourier transform to identify songs. In speech recognition, the Fourier transform and related transforms are used to reconstruct spoken words.

In addition, the Fourier transform is quite useful for image processing. The JPEG compression algorithm is a special case of the Fourier transform used to remove high-frequency components from images.

Personally, I has been applied the fast Fourier transform (or just FFT) for creating image replicas during the reconstruction procedure — this method suits when we don’t have an access to micro-CT scanners, but need some binary images to study main properties of rock samples.

By the way, recently I wrote a post about binary images:

The Brief History of Binary Images

Below I’ll consider a bit simpler case of removing systematic noise from the input image.

This is the original photo we will be working with:

Let’s read the image with a help of imread function from skimage package and then apply the FFT on it.

The Python code:

import matplotlib.pyplot as plt
import numpy as np
from skimage.io import imread, imshow
from skimage.color import rgb2gray

# read input image
my_im = imread('photo.jpg')
plt.figure('Input Image')
plt.imshow(my_im)
plt.axis('off')  # hide axis
plt.show()

# convert the image to grayscale
gray_im = rgb2gray(my_im)

# applying FFT and center shift
fourier_im = np.fft.fft2(gray_im)
im_shift = np.fft.fftshift(fourier_im)
plt.figure('Applying FFT')
plt.imshow(np.log(abs(im_shift)), cmap='gray')
plt.tight_layout()
plt.show()

The output:

Here it’s possible to notice two image distortions in a form of crossed lines — they are directly associated to horizontal (clouds) and vertical (street lamp) elements of the photo.

But what if we try to remove the horizontal “noise” associated with clouds in a photograph?

We can use a mask which is created by initializing a zero matrix of the same size as the image in the frequency domain. Central vertical and horizontal strips of ones is set in the mask. Then the mask is applied to the shifted Fourier-transformed image by element-wise multiplication. After filtering, we perform an inverse FFT on the masked frequency data to convert it back to the spatial domain.

# create vertical & horizontal mask for noise removal
rows, cols = gray_im.shape
crow, ccol = rows // 2, cols // 2

# create a mask with ones in the vertical and horizontal strip
# let's say width is equal to 100 pixels
mask = np.zeros((rows, cols), dtype=np.float32)
mask[crow - 50:crow + 50, :] = 1  # vertical strip in the center
mask[:, ccol - 50:ccol + 50] = 1  # horizontal strip in the center

# apply the mask to the shifted FFT
filtered_im_shift = im_shift * mask

# inverse FFT to get the filtered image back
filtered_fourier_im = np.fft.ifftshift(filtered_im_shift)
filtered_image = np.fft.ifft2(filtered_fourier_im)
filtered_image = np.abs(filtered_image)  # Take absolute value

# display the filtered image
plt.figure('Filtered Image')
plt.imshow(filtered_image, cmap='gray')
plt.axis('off')  # hide axis
plt.tight_layout()
plt.show()

And the result will look as follows:

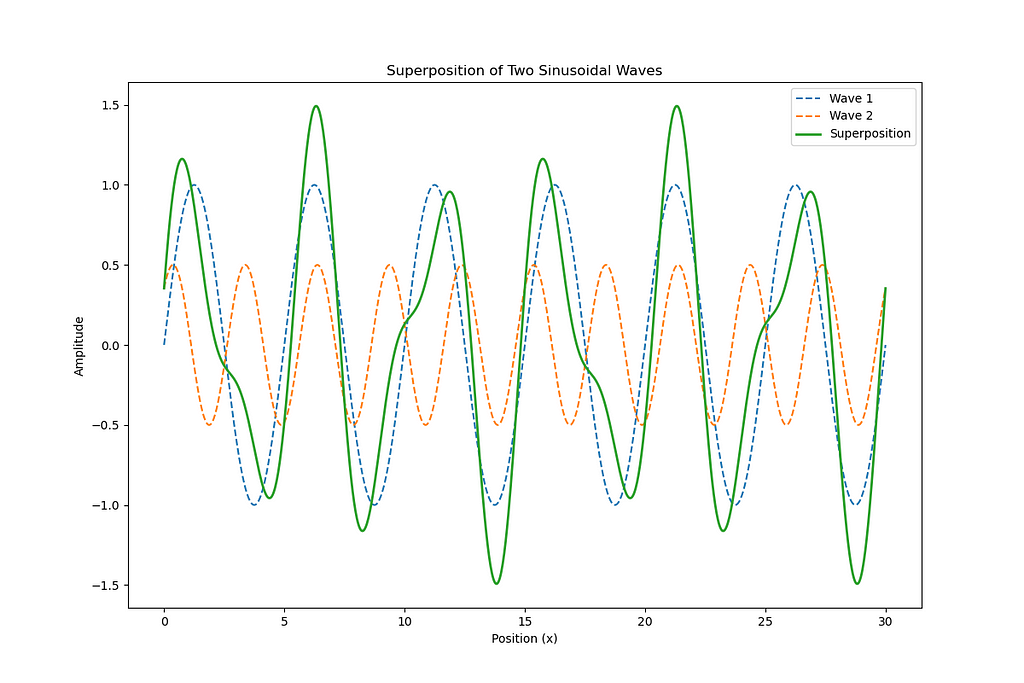
Case # 2: Superposition principle

The superposition principle is a fundamental concept in physics and engineering, particularly in the fields of wave mechanics, optics, and signal processing. It states that when two or more waves overlap in space, the resultant wave at any point is the sum of the individual waves at that point. This principle applies to linear systems and is crucial for understanding phenomena such as interference and diffraction.

In the context of STEM (Science, Technology, Engineering, and Mathematics), the superposition principle can be applied to analyze various types of waves, including sound waves, electromagnetic waves, and quantum wave functions. It allows engineers and scientists to predict how waves interact with each other, which is essential for designing systems like communication networks, audio equipment, and optical devices.

Mathematical representation

For two sinusoidal waves described by the following equations:

y₁(x, t) = A₁ sin(k₁ x - ω₁ t + φ₁)
y₂(x, t) = A₂ sin(k₂ x - ω₂ t + φ₂) 

The resultant wave y(x, t) due to the superposition of these two waves can be expressed as:

y(x, t) = y₁(x, t) + y₂(x, t)

In the above equations A₁ and A₂ are the amplitudes of the waves; k₁ and k₂ are the wave numbers; ω₁ and ω₂ are the angular frequencies; φ₁ and φ₂ are the phase shifts.

Python Script to Calculate Superposition of Two Sinusoidal Waves

Below is a Python script that calculates and visualizes the superposition of two sinusoidal waves using numpy and matplotlib. The script generates two sinusoidal waves with specified parameters and plots their superposition.

import numpy as np
import matplotlib.pyplot as plt

# parameters for the first wave
A1 = 1.0      # amplitude
k1 = 2 * np.pi / 5  # wave number (2*pi/wavelength)
omega1 = 2 * np.pi / 10  # angular frequency (2*pi/period)
phi1 = 0      # phase shift

# parameters for the second wave
A2 = 0.5      # amplitude
k2 = 2 * np.pi / 3   # wave number
omega2 = 2 * np.pi / 15  # angular frequency
phi2 = np.pi / 4  # phase shift

# create an array of x values
x = np.linspace(0, 30, 1000)
t = 0  # time at which we calculate the waves

# calculate the individual waves
y1 = A1 * np.sin(k1 * x - omega1 * t + phi1)
y2 = A2 * np.sin(k2 * x - omega2 * t + phi2)

# calculate the superposition of the two waves
y_superposition = y1 + y2

# plotting
plt.figure(figsize=(12, 8))
plt.plot(x, y1, label='Wave 1', linestyle='--')
plt.plot(x, y2, label='Wave 2', linestyle='--')
plt.plot(x, y_superposition, label='Superposition', linewidth=2)
plt.title('Superposition of Two Sinusoidal Waves')
plt.xlabel('Position (x)')
plt.ylabel('Amplitude')
plt.legend()
plt.show()

The output is:

Case # 3: Material balance

The last case of applying scientific methods is a bit ‘theoretical’ one, so I’m not going to insert complicated formulae here at all.

I decided to mention material balance in my post about STEM, because any Data Scientist somehow knows a famous the “garbage in, garbage out” (or just GIGO) formula meaning that low-quality input will produce faulty output, which, I believe, is one of the forms of material balance in Data Science 🙂

The GIGO principle in Data Science refers to the idea that the quality of output is determined by the quality of the input. If you provide poor-quality, inaccurate, or irrelevant data (garbage in), the results of your analysis, models, or algorithms will also be flawed or misleading (garbage out). This emphasizes the importance of data quality, cleanliness, and relevance in data science projects, as well as the need for proper data preprocessing and validation to ensure reliable outcomes.

Conclusion

STEM background provides a robust foundation for Data Science, enhancing analytical skills essential for interpreting complex datasets. First, the mathematical principles underpinning statistics and algorithms enable data scientists to develop models that accurately predict trends and behaviors. Second, the scientific method fosters critical thinking and problem-solving abilities, allowing practitioners to formulate hypotheses, conduct experiments, and validate findings systematically. Finally, engineering principles are crucial for building scalable data infrastructures and optimizing performance, ensuring that data solutions are not only effective but also efficient. Together, these STEM disciplines empower Data Scientists to approach challenges with a structured mindset, driving innovation and informed decision-making in an increasingly data-driven world.

I tried to provide 3 simple cases from my personal experience of showing how important STEM education can be for those who want to enter the Data universe. But, of course, much more examples exist in reality, and Noble Prize-2024 in Physics is another bright showcase of STEM importance for DS and ML development. This year’s award was given “for foundational discoveries and inventions that enable machine learning with artificial neural networks.”

Thanks for reading! Although I recommend not just to read about someone else’s experience, but rather to try implement STEM principles in your next Data Science project to see the whole depth behind it 🙂

Why STEM Is Important for Any Data Scientist was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.