Why Sets are so useful in programming

Why Sets Are So Useful in Programming

And how you can use them to boost your code performance

A set is a simple structure defined as a collection of distinct elements. Sets are most commonly seen in fields like mathematics or logic, but they’re also useful in programming for writing efficient code. In this article, I detail cases where sets outperform alternative data types like lists, and the underlying implementation of sets which makes them so useful to programmers.

A set is an example of a container; these are used to store several elements under one variable. When looking for a container datatype, lists (typically defined with square brackets [ ]) are the go-to choice, being used extensively in almost all programming languages. Sets bare a lot of similarity to lists, most notably as they are both dynamic, allowing their size to grow or shrink as needed. The only differences lie in that lists preserve order of elements and allow duplicates, whereas sets do neither, offering a unique advantage in certain scenarios. By knowing when to choose sets over lists, you can greatly enhance the performance of your programs and improve code readability.

In Python, sets can be declared using curly braces, or by using the set constructor.

set_a = {1, 4, 9, 16}
set_b = set([1,2,3]) #coverting list to set
empty_set = set()

Sets do not contain duplicates

A defining property of a set is that each element is distinct, or unique, so there are no repeated entries. A simple application of this could be to remove all duplicate entries in a list by converting the list into a set.

#LIST Implementation O(n^2)
def remove_duplicate_entries(list input_list):
    output_list = []
    for element in input_list:
        if element in output_list: 
             output_list.append(element)
    return output_list

#SET Implementation O(n)
def remove_duplicate_entries(list input_list):
    return list(set(input_list))

Because a set is used here, the order of the list is not preserved. Use an implementation like the first one if order matters.

The next function identifies if a list contains any duplicates; the order of elements is not here important, only the occurrence of duplicates. The set implementation is much more desirable as operations on sets are typically much faster than on lists (this is explained in more detail later).

#LIST Implementation
def has_duplicates(list input_list):
    unique_elements = []
    for element in input_list:
        if element in unique_elements: 
             return True
        else:
             unique_elements.append(element)
    return False

#SET Implementation
def has_duplicates(list input_list): 
    return len(input_list) != len(set(input_list))

Note: In cases where a duplicate element appears early, the first implementation can outperform the second as it catches the duplicate early and returns False without checking every entry, whereas the second implementation always iterates through every element. A more optimal solution would involve a similar method to the first implementation but using a set as the unique_elements container.

def has_duplicates(list input_list) -> bool:
    unique_elements = set() #**modified here
    for element in input_list:
        if element in unique_elements: 
             return True
        else:
             unique_elements.add(element)
    return False

Even if these applications seem quite crude or simplistic, there are countless uses built upon the principle of “removing duplicates” that take some creativity to see. For example, Leetcode 1832 ‘Check if the Sentence is a Pangram’- where you need to detects if all 26 letters have been used in an input sentence- can be elegantly solved using a set comprehension.

def is_pangram(str sentence) -> bool:
    present_letters = {letter for letter in sentence}
    return len(present_letters) == 26

Without sets, this problem would need to utilise nested looping which is both harder to write, and less efficient with a complexity of O(n^2).

The key to identifying cases where sets are useful is by considering:

• If we only care about an occurrence, like in this problem if the sentence contained the word ‘eel’, we only care that the letter ‘e’ occurred, not that it occurred twice so we can discard the second and any future ‘e’s.
• Building on this principal, in cases where a list is very large, it may be desirable to remove duplicate elements to continue processing on a much smaller list.
• If we don’t care about the order of elements. In cases where maintaining order is important, like in a priority queue, lists should instead be used.

Hash maps and lack of order

Taking a step back, it might seem that easy duplicate removal is the only benefit of using sets. We previously discussed how sets have no order; arrays have indexed element which could simply ignored and treated like a set. It appears that arrays can do the same job as a set, if not more.

However, this simplification enforced by sets opens way to different underlying implementations. In lists, elements are assigned indices to give each element a place in the order. Sets have no need to assign indices, so they instead implement a different approach of referencing: hash mapping. These operate by (pseudo)randomly allocating addresses to elements, as opposed to storing them in a row. The allocation is governed by hashing functions, which use the element as an input to output an address.

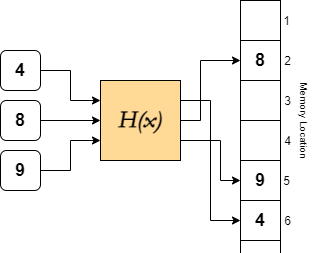
H(x) is deterministic, so the same input always gives the same output, ie. there is no RNG within the function H, so H(4) = 6 always in this case.

Running this function takes the same amount of time regardless of the size of the set, ie. hashing has O(1) time complexity. This means that the time taken to hash is independent of the size of the list, and remains at a constant, quick speed.

Set operations

Because hashing is generally quick, a whole host of operations that are typically slow on large arrays can be executed very efficiently on a set.

Search or Membership Testing

Searching for elements in an array utilises an algorithm called Linear Search, by checking each item in the list one by one. In the worst case, where the item being searched for does not exist in the list, the algorithm traverses every element of the list (O(n)). In a very large list, this process takes a long time.

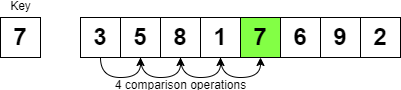
However, as hashing is O(1), Python hashes the item to be found, and either returns where it is in memory, or that it doesn’t exist- in a very small amount of time.

number_list = range(random.randint(1,000,000))
number_set = set(number_list)

#Line 1
#BEGIN TIMER
print(-1 in number_list)
#END TIMER

#Line 2
#BEGIN TIMER
print(-1 in number_set)
#END TIMER

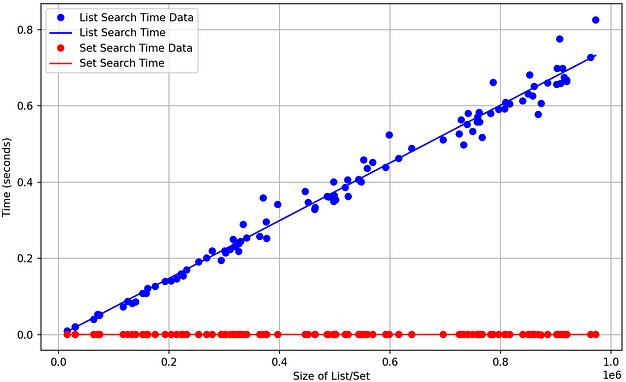
Note: Searching using a hashmap has an amortized time complexity of O(1). This means that in the average case, it runs at constant time but technically, in the worst case, searching is O(n). However, this is extremely unlikely and comes down to the hashing implementation having a chance of collisions, which is when multiple elements in a hashmap/set are hashed to the same address.

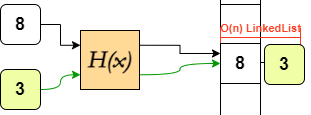
Deletion

Deleting an element from a list first involves a search to locate the element, and then removing reference to the element by clearing the address. In an array, after the O(n) time search, the index of every element following the deleted element needs to be shifted down one. This itself is another O(n) process.

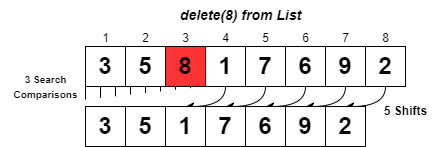
Deleting an element from a set involves the O(1) lookup, and then erasure of the memory address which is an O(1) process so deletion also operates in constant time. Sets also have more ways to delete elements, such that errors are not raised, or such that multiple elements can be removed concisely.

#LIST
numbers = [1, 3, 4, 7, 8, 11]

numbers.remove(4)
numbers.remove(5) #Raises ERROR as 5 is not in list
numbers.pop(0) #Deletes number at index 0, ie. 1

#SET
numbers = {1, 3, 4, 7, 8, 11}

numbers.remove(4)
numbers.remove(5) #Raises ERROR as 5 is not in set
numbers.discard(5) #Does not raise error if 5 is not in the set
numbers -= {1,2,3} #Performs set difference, ie. 1, 3 are discarded

Insertion

Both appending to a list and adding elements to a set are constant operations; adding to a specified index in a list (.insert) however comes with the added time to shift elements around.

num_list = [1,2,3]
num_set = {1,2,3}

num_list.append(4)
num_set.add(4)

num_list += [5,6,7]
num_set += {5,6,7}

Advanced Set Operations

Additionally, all the mathematical operations that can be performed on sets have implementation in python also. These operations are once again time consuming to manually perform on a list, and are once again optimised using hashing.

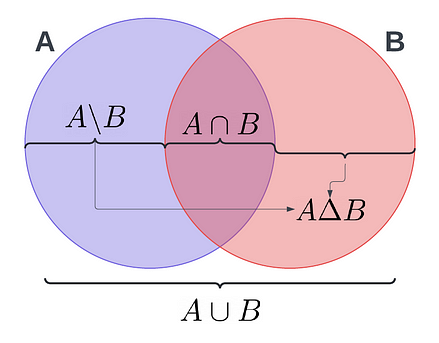
A = {1, 2, 3, 5, 8, 13}
B = {2, 3, 5, 7, 13, 17}

# A n B
AintersectB = A & B
# A U B
AunionB = A | B
# A  B
AminusB = A - B
# A U B - A n B or A Delta B
AsymmetricdiffB = A ^ B

This also includes comparison operators, namely proper and relaxed subsets and supersets. These operations once again run much faster than their list counterparts, operating in O(n) time, where n is the larger of the 2 sets.

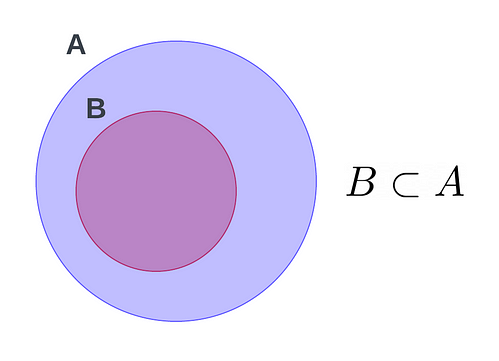
A <= B #A is a proper subset of B
A > B #A is a superset of B

Frozen Sets

A final small, but underrated feature in python is the frozen set, which is essentially a read-only or immutable set. These offer greater memory efficiency and could be useful in cases where you frequently test membership in a tuple.

Conclusion

The essence of using sets to boost performance is encapsulated by the principle of optimisation by reduction.

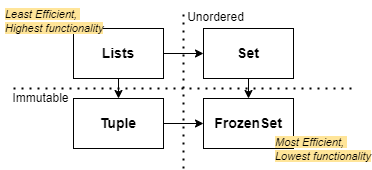
Data structures like lists have the most functionality- being indexed and dynamic- but come at the cost of comparatively lower efficiency: speed and memory-wise. Identifying which features are essential vs unused to inform what data type to use will result in code that runs faster and reads better.

All technical diagrams by author.

Why Sets are so useful in programming was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.