Why Scaling Works: Inductive Biases vs The Bitter Lesson

Building deep insights with a toy problem

Over the past decade we’ve witnessed the power of scaling deep learning models. Larger models, trained on heaps of data, consistently outperform previous methods in language modelling, image generation, playing games, and even protein folding. To understand why scaling works, let’s look at a toy problem.

Introducing the Problem

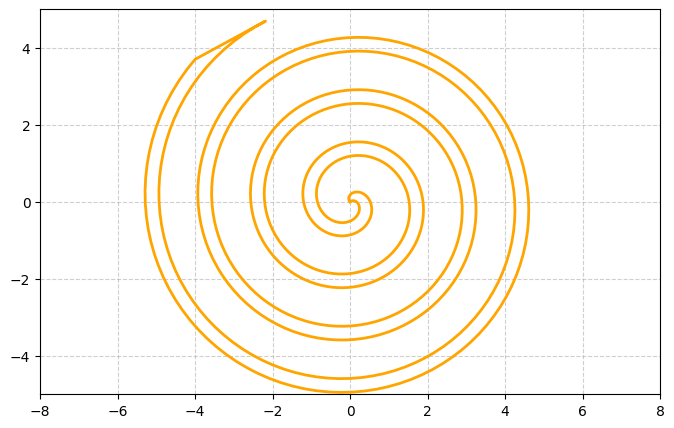
We start with a 1D manifold weaving its way through the 2D plane and forming a spiral:

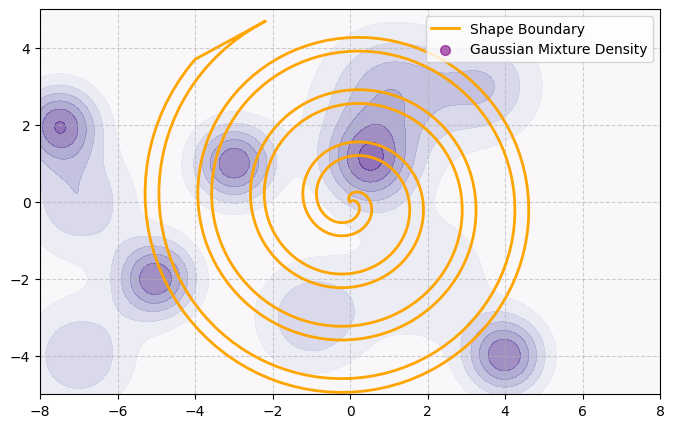
Now we add a heatmap which represents the probability density of sampling a particular 2D point. Notably, this probability density is independent of the shape of the manifold:

Let’s assume that the data on either side of the manifold is always completely separable (i.e. there is no noise). Datapoints on the outside of the manifold are blue and those on the inside are orange. If we draw a sample of N=1000 points it may look like this:

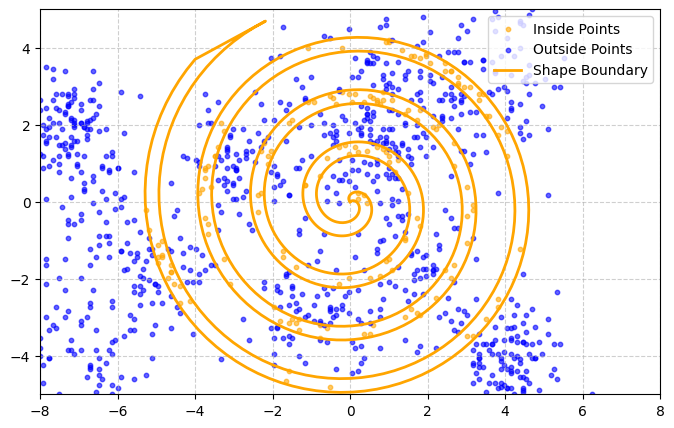
Toy problem: How do we build a model which predicts the colour of a point based on its 2D coordinates?

In the real world we often can’t sample uniformly from all parts of the feature space. For example, in image classification it’s easy to find images of trees in general but less easy to find many examples of specific trees. As a result, it may be harder for a model to learn the difference between species there aren’t many examples of. Similarly, in our toy problem, different parts of the space will become difficult to predict simply because they are harder to sample.

Solving the Toy Problem

First, we build a simple neural network with 3 layers, running for 1000 epochs. The neural network’s predictions are heavily influenced by the particulars of the sample. As a result, the trained model has difficulty inferring the shape of the manifold just because of sampling sparsity:

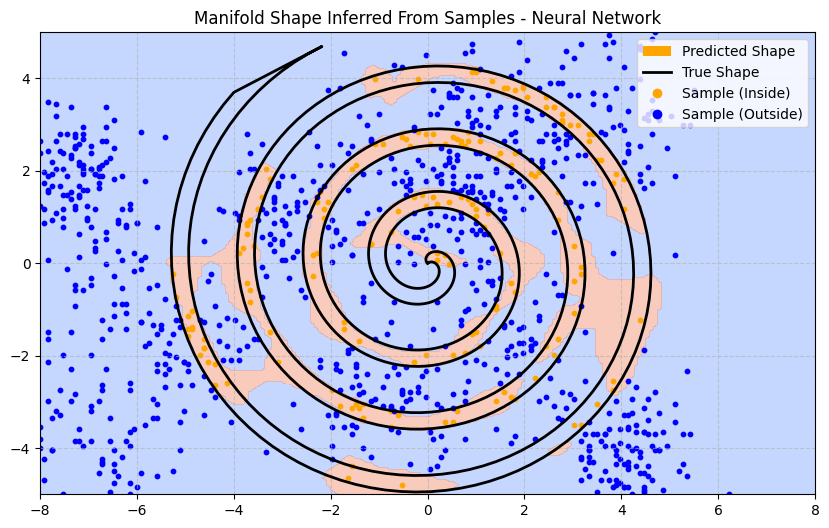
Even knowing that the points are completely separable, there are infinitely many ways to draw a boundary around the sampled points. Based on the sample data, why should any one boundary be considered superior to another?

With regularisation techniques we could encourage the model to produce a smoother boundary rather than curving tightly around predicted points. That helps to an extent but it won’t solve our problem in regions of sparsity.

Since we already know the manifold is a spiral, can we encourage the model to make spiral-like predictions?

We can add what’s called an “inductive prior”: something we put in the model architecture or the training process which contains information about the problem space. In this toy problem we can do some feature engineering and adjust the way we present inputs to the model. Instead of 2D (x, y) coordinates, we transform the input into polar coordinates (r, θ).

Now the neural network can make predictions based on the distance and angle from the origin. This biases the model towards producing decision boundaries which are more curved. Here is how the newly trained model predicts the decision boundary:

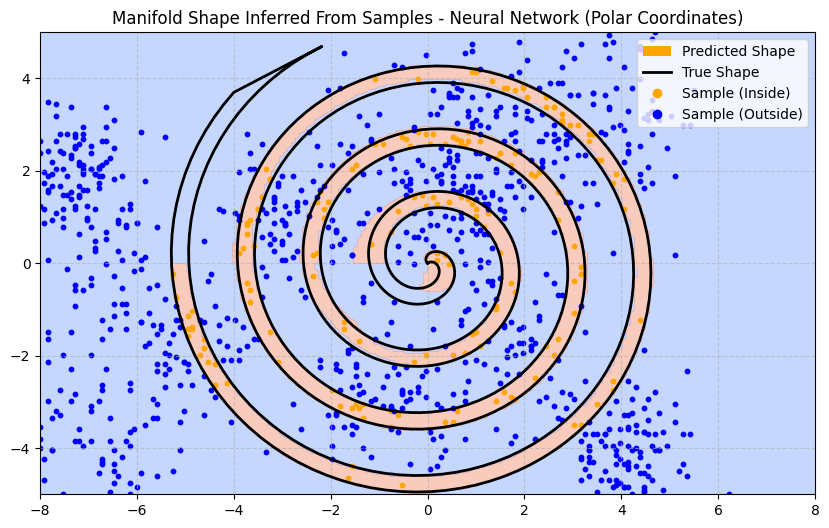
Notice how much better the model performs in parts of the input space where there are no samples. The feature of those missing points remain similar to features of observed points and so the model can predict an effective boundary without seeing additional data.

Obviously, inductive priors are useful.

Most architecture decisions will induce an inductive prior. Let’s try some enhancements and try to think about what kind of inductive prior they introduce:

1. Focal Loss — increases the loss on data points the model finds hard to predict. This might improve accuracy at the cost of increasing the model complexity around those points (as we would expect from the bias-variance trade-off). To reduce the impact of increased variance we can add some regularisation.
2. Weight Decay — L2 norm on the size of the weights prevents the model from learning features weighted too strongly to any one sample.
3. Layer Norm — has a lot of subtle effects, one of which could be that the model focuses more on the relationships between points rather than their magnitude, which might help offset the increased variance from using Focal Loss.

After making all of these improvements, how much better does our predicted manifold look?

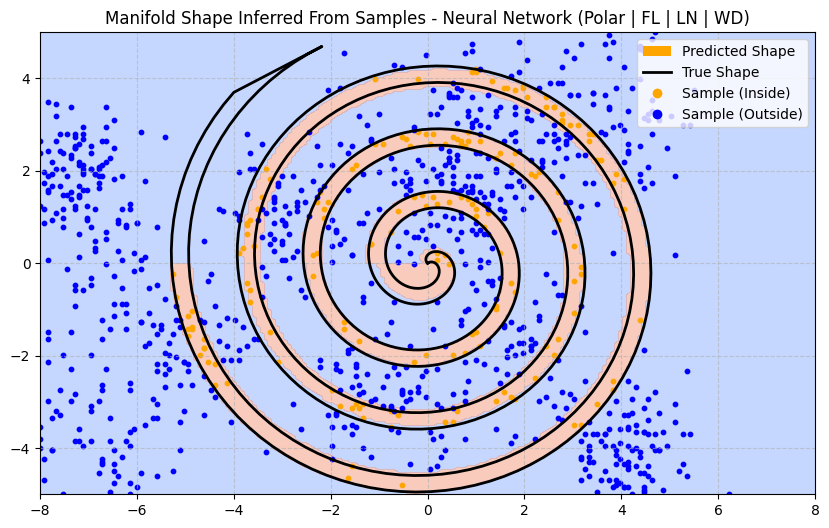
Not much better at all. In fact, it’s introduced an artefact near the centre of the spiral. And it’s still failed to predict anything at the end of the spiral (in the upper-left quadrant) where there is no data. That said, it has managed to capture more of the curve near the origin which is a plus.

The Bitter Lesson

Now suppose that another research team has no idea that there’s a hard boundary in the shape of a single continuous spiral. For all they know there could be pockets inside pockets with fuzzy probabilistic boundaries.

However, this team is able to collect a sample of 10,000 instead of 1,000. For their model they just use a k-Nearest Neighbour (kNN) approach with k=5.

Side note: k=5 is a poor inductive prior here. For this problem k=1 is generally better. Challenge: can you figure out why? Add a comment to this article with your answer.

Now, kNN is not a particularly powerful algorithm compared to a neural network. However, even with a bad inductive prior here is how the kNN solution scales with 10x more data:

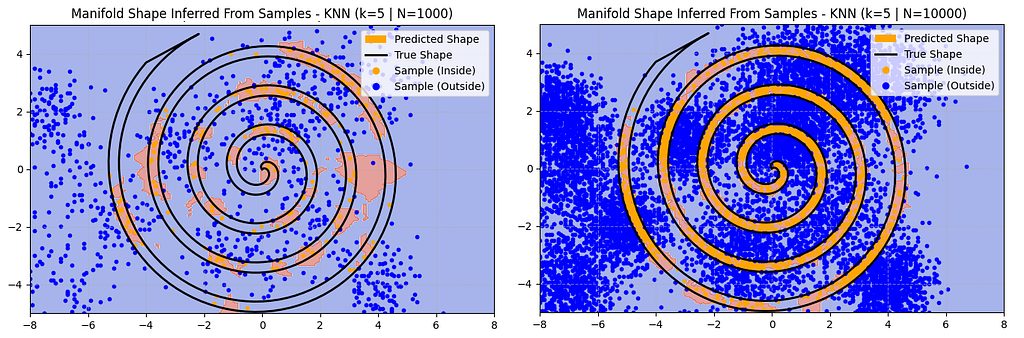
With 10x more data the kNN approach is performing closer to the neural network. In particular it’s better at predicting the shape at the tails of the spiral, although it’s still missing that hard to sample upper-left quadrant. It’s also making some mistakes, often producing a fuzzier border.

What if we added 100x or 1000x more data? Let’s see how both the kNN vs Neural Network approaches compare as we scale the amount of data used:

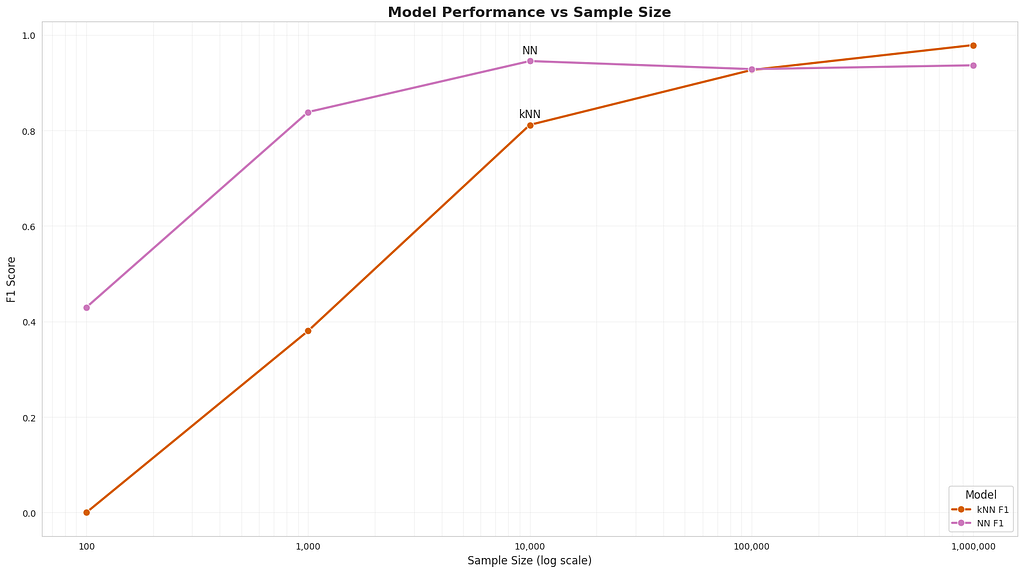
As we increase the size of the training data it largely doesn’t matter which model we use. What’s more, given enough data, the lowly kNN actually starts to perform better than our carefully crafted neural network with well thought out inductive priors.

This is a big lesson. As a field, we still have not thoroughly learned it, as we are continuing to make the same kind of mistakes. To see this, and to effectively resist it, we have to understand the appeal of these mistakes. We have to learn the bitter lesson that building in how we think we think does not work in the long run. The bitter lesson is based on the historical observations that 1) AI researchers have often tried to build knowledge into their agents, 2) this always helps in the short term, and is personally satisfying to the researcher, but 3) in the long run it plateaus and even inhibits further progress, and 4) breakthrough progress eventually arrives by an opposing approach based on scaling computation by search and learning. The eventual success is tinged with bitterness, and often incompletely digested, because it is success over a favored, human-centric approach.

From Rich Sutton’s essay “The Bitter Lesson”

Superior inductive priors are no match for just using more compute to solve the problem. In this case, “more compute” just involves storing a larger sample of data in memory and using kNN to match to the nearest neighbours. We’ve seen this play out with transformer-based Large Language Models (LLMs). They continue to overpower other Natural Language Processing techniques simply by training larger and larger models, with more and more GPUs, on more and more text data.

But Surely…?

This toy example has a subtle issue we’ve seen pop up with both models: failing to predict that sparse section of the spiral in the upper-left quadrant. This is particularly relevant to Large Language Models, training reasoning capabilities, and our quest towards “Artificial General Intelligence” (AGI). To see what I mean let’s zoom in on that unusual shaped tail in the upper-left.

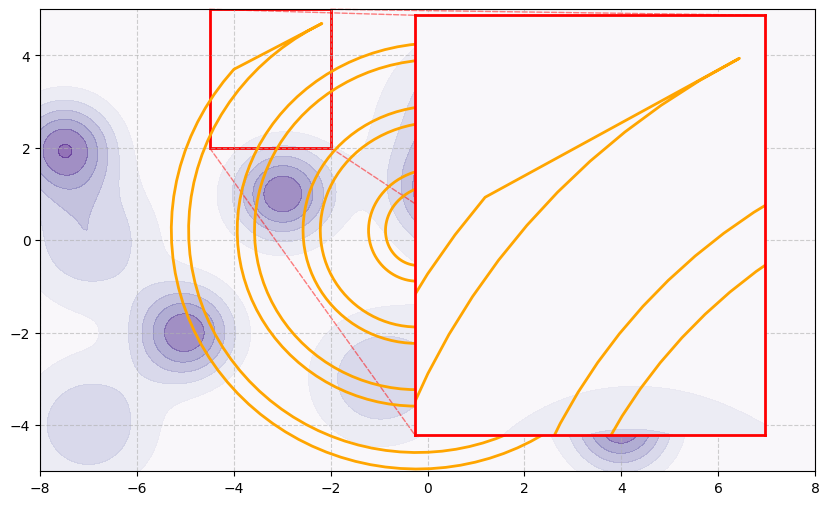
This region has a particularly low sampling density and the boundary is quite different to the rest of the manifold. Suppose this area is something we care a lot about, for example: generating “reasoning” from a Large Language Model (LLM). Not only is such data rare (if randomly sampled) but it is sufficiently different to the rest of the data, which means features from other parts of the space are not useful in making predictions here. Additionally, notice how sharp and specific the boundary is — points sampled near the tip could very easily fall on the outside.

Let’s see how this compares to a simplified view of training an LLM on text-based reasoning:

1. Reasoning is complicated and we probably won’t find a solution by fitting a “smooth” line that averages out a few samples. To solve a reasoning problem it’s not enough to follow an apparent pattern but it’s necessary to really understand the problem. Training a model to reason will likely need a lot of data.
2. Randomly sampling data from the internet doesn’t give us many samples where humans explain intricate mental reasoning steps required to get to an answer. Paying people to explicitly generate reasoning data may help increase the density. But it’s a slow process and the amount of data needed is actually quite high.
3. We care a lot about getting it right because reasoning abilities would open up a lot more use cases for AI.

Of course reasoning is more complex than predicting the tip of this spiral. There are usually multiple ways to get to a correct answer, there may be many correct answers, and sometimes the boundary can be fuzzy. However, we are also not without inductive priors in deep learning architectures, including techniques using reinforcement learning.

In our toy problem there is regularity in the shape of the boundary and so we used an inductive prior to encourage the model to learn that shape. When modelling reasoning, if we could construct a manifold in a higher dimensional space representing concepts and ideas, there would be some regularity to its shape that could be exploited for an inductive prior. If The Bitter Lesson continues to hold then we would assume the search for such an inductive prior is not the path forward. We just need to scale compute. And so far the best way to do that is to collect more data and throw it at larger models.

But surely, I hear you say, transformers were so successful because the attention mechanism introduced a strong inductive prior into language modelling? The paper “Were RNNs all we needed” suggests that a simplified Recurrent Neural Network (RNN) can also perform well if scaled up. It’s not because of an inductive prior. It’s because the paper improved the speed with which we can train an RNN on large amounts of data. And that’s why transformers are so effective — parallelism allowed us to leverage much more compute. It’s an architecture straight from the heart of The Bitter Lesson.

Running Out of Data?

There’s always more data. Synthetic data or reinforcement learning techniques like self-play can generate infinite data. Although without connection to the real world the validity of that data can get fuzzy. That’s why techniques like RLHF have hand crafted data as a base — so that the model of human preferences can be as accurate as possible. Also, given that reasoning is often mathematical, it may be easy to generate such data using automated methods.

Now the question is: given the current inductive priors we have, how much data would it take to train models with true reasoning capability?

If The Bitter Lesson continues to apply the answer is: it doesn’t matter, finding better ways to leverage more compute will continue to give better gains than trying to find superior inductive priors^. This means that the search for ever more powerful AI is firmly in the domain of the companies with the biggest budgets.

And after writing all of this… I still hope that’s not true.

About me

I’m the Lead AI Engineer @ Affinda. Check out our AI Document Automation Case Studies to learn more.

Some of my long reads:

• What do Large Language Models “Understand”?
• Exploring the AI Alignment Problem with GridWorlds

More practical reads:

• 5 Hidden Risks in Deploying Generative AI
• How I Deal with Hallucinations at an AI Startup

Appendix

^ It’s important to note that the essay “The Bitter Lesson” isn’t explicitly about inductive biases vs collecting more data. Throwing more data at bigger models is one way to leverage more compute. And in deep learning that usually means finding better ways to increase parallelism in training. Lately it’s also about leveraging more inference time compute (e.g. o1-preview). There may yet be other ways. The topic is slightly more nuanced than I’ve presented here in this short article.

Why Scaling Works: Inductive Biases vs The Bitter Lesson was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.