
This post covers my recent paper Cluster and Separate: A GNN Approach to Voice and Staff Prediction for Score Engraving published at ISMIR 2024

Introduction
Music encoded in formats like MIDI, even when it includes quantized notes, time signatures, or bar information, often lacks important elements for visualization such as voice and staff information. This limitation also applies to the output from music generation, transcription, or arrangement systems. As a result, such music can’t be easily transformed into a readable musical score for human musicians to interpret and perform.
It’s worth noting that voice and staff separation are just two of many aspects — others include pitch spelling, rhythmic grouping, and tuplet creation — that a score engraving system might address.
In musical terms, “voice” often refers to a sequence of non-overlapping notes, typically called a monophonic voice. However, this definition falls short when dealing with polyphonic instruments. For example, voices can also include chords, which are groups of notes played simultaneously, perceived as a single unit. In this context, we refer to such a voice, capable of containing chords, as a homophonic voice.
The problem
Separating the notes from a quantized symbolic music piece (e.g., a MIDI file) into multiple voices and staves is an important and non-trivial task. It is a fundamental part of the larger task of music score engraving (or score type-setting), which aims to produce readable musical scores for human performers.
The musical score is an important tool for musicians due to its ability to convey musical information in a compact graphical form. Compared to other music representations that may be easier to define and process for machines, such as MIDI files, the musical score is characterized by how efficiently trained musicians can read it.

Given a Quantized Midi there are many possibilities for transforming it to a readable format, which mostly consists of separating the notes into voices and staves.
See below two of these possibilities. They demonstrate how engraving systems usually work.

The big question is how can we make automatic transcription models better.
Motivation
To develop a more effective system for separating musical notes into voices and staves, particularly for complex piano music, we need to rethink the problem from a different perspective. We aim to improve the readability of transcribed music starting from a quantized MIDI, which is important for creating good score engravings and better performance by musicians.
For good score readability, two elements are probably the most important:
- the separation of staves, which organizes the notes between the top and bottom staff;
- and the separation of voices, highlighted in this picture with lines of different colors.

In piano scores, as said before, voices are not strictly monophonic but homophonic, which means a single voice can contain one or multiple notes playing at the same time. From now on, we call these chords. You can see some examples of chord highlighted in purple in the bottom staff of the picture above.
From a machine-learning perspective, we have two tasks to solve:
- The first is staff separation, which is straightforward, we just need to predict for each note a binary label, for top or bottom staff specifically for piano scores.
- The voice separation task may seem similar, after all, if we can predict the voice number for each voice, with a multiclass classifier, and the problem would be solved!
However, directly predicting voice labels is problematic. We would need to fix the maximum number of voices the system can accept, but this creates a trade-off between our system flexibility and the class imbalance within the data.
For example, if we set the maximum number of voices to 8, to account for 4 in each staff as it is commonly done in music notation software, we can expect to have very few occurrences of labels 8 and 4 in our dataset.
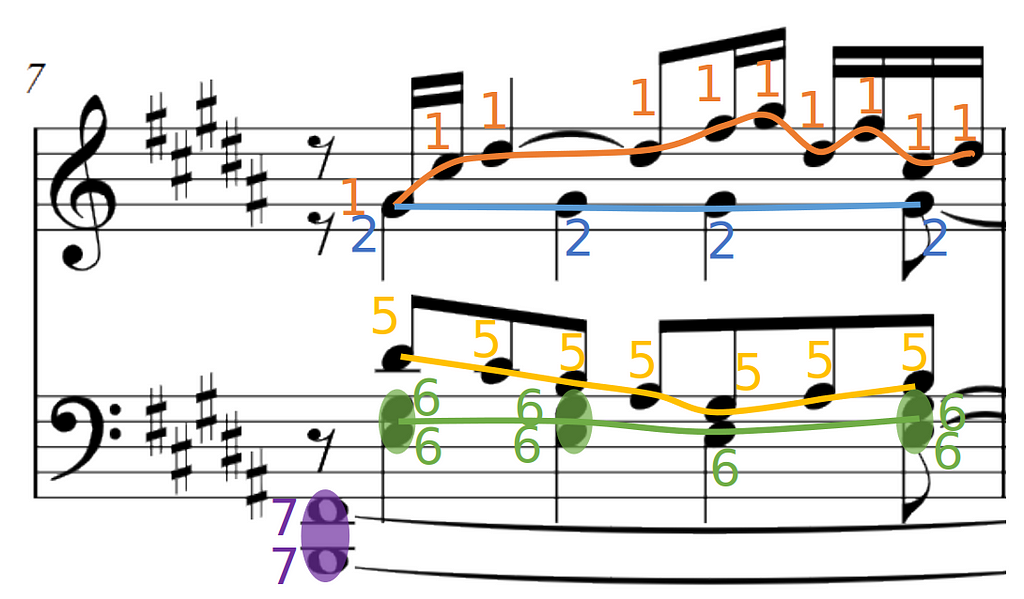
Looking specifically at the score excerpt here, voices 3,4, and 8 are completely missing. Highly imbalanced data will degrade the performance of a multilabel classifier and if we set a lower number of voices, we would lose system flexibility.
Methodology
The solution to these problems is to be able to translate the knowledge the system learned on some voices, to other voices. For this, we abandon the idea of the multiclass classifier, and frame the voice prediction as a link prediction problem. We want to link two notes if they are consecutive in the same voice. This has the advantage of breaking a complex problem into a set of very simple problems where for each pair of notes we predict again a binary label telling whether the two notes are linked or not. This approach is also valid for chords, as you see in the low voice of this picture.
This process will create a graph which we call an output graph. To find the voices we can simply compute the connected components of the output graph!
To re-iterate, we formulate the problem of voice and staff separation as two binary prediction tasks.
- For staff separation, we predict the staff number for each note,
- and to separate voices we predict links between each pair of notes.
While not strictly necessary, we found it useful for the performance of our system to add an extra task:
- Chord prediction, where similar to voice, we link each pair of notes if they belong to the same chord.
Let’s recap what our system looks like until now, we have three binary classifiers, one that inputs single notes, and two that input pairs of notes. What we need now are good input features, so our classifiers can use contextual information in their prediction. Using deep learning vocabulary, we need a good note encoder!
We choose to use a Graph Neural Network (GNN) as a note encoder as it often excels in symbolic music processing. Therefore we need to create a graph from the musical input.
For this, we deterministically build a new graph from the Quantized midi, which we call input graph.
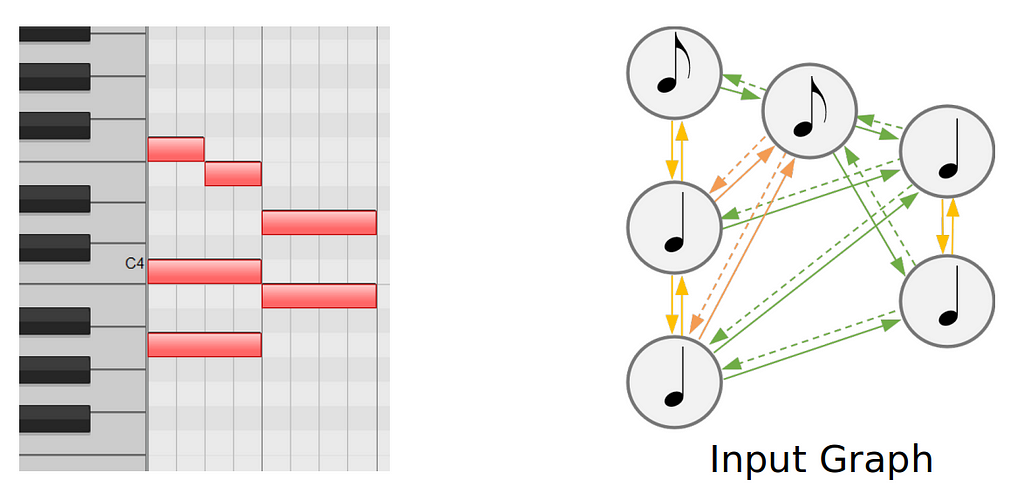
Creating these input graph can be done easily with tools such as GraphMuse.
Now, putting everything together, our model looks something like this:

- It starts with some quantized midi which is preprocessed to a graph to create the input graph.
- The input graph goes through a Graph Neural Network (GNN) to create an intermediate latent representation for every note. We encode every note therefore we call this part, the GNN encoder;
- Then we feed this to a shallow MLP classifier for our three tasks, voice, staff, and chord prediction. We can also call this part the decoder;
- After the prediction, we obtain an output graph.
The approach until now, can be seen as a graph-to-graph approach, where we start from the input graph that we built from the MIDI, to predict the output graph containing voice and chord links and staff labels.
5. For the final step, our output graph goes through a postprocessing routine to create a beautiful and easy-to-read musical score.
The goal of the postprocessing is to remove configurations that could lead to an invalid output, such as a voice splitting into two voices. To mitigate these issues:
- we cluster the notes that belong to the same chord according to the chord prediction head
- We ensure every node has a maximum of one incoming and outgoing edge by applying a linear assignment solution;
- And, finally, propagate the information back to the original nodes.

One of the standout features of our system is its ability to outperform other existing systems in music analysis and score engraving. Unlike traditional approaches that rely on musical heuristics — which can sometimes be unreliable — our system avoids these issues by maintaining a simple but robust approach. Furthermore, our system is able to compute a global solution for the entire piece, without segmentation due to its low memory and computational requirements. Additionally, it is capable of handling an unlimited number of voices, making it a more flexible and powerful tool for complex musical works. These advantages highlight the system’s robust design and its capacity to tackle challenges in music processing with greater precision and efficiency.
Datasets
To train and evaluate our system we used two datasets. The J-pop dataset, which contains 811 pop piano scores, and the DCML romantic corpus which contains 393 romantic music piano scores. Comparatively, the DCML corpus is much more complex, since it contains scores that present a number of difficulties such as a high number of voices, voice crossing, and staff crossing. Using a combination of complex and simpler data we can train a system that remains robust and flexible to diverse types of input.
Visualizing the Predictions
To accompany our system, we also developed a web interface where the input and output graphs can be visualized and explored, to debug complex cases, or simply to have a better understanding of the graph creation process. Check it out here.
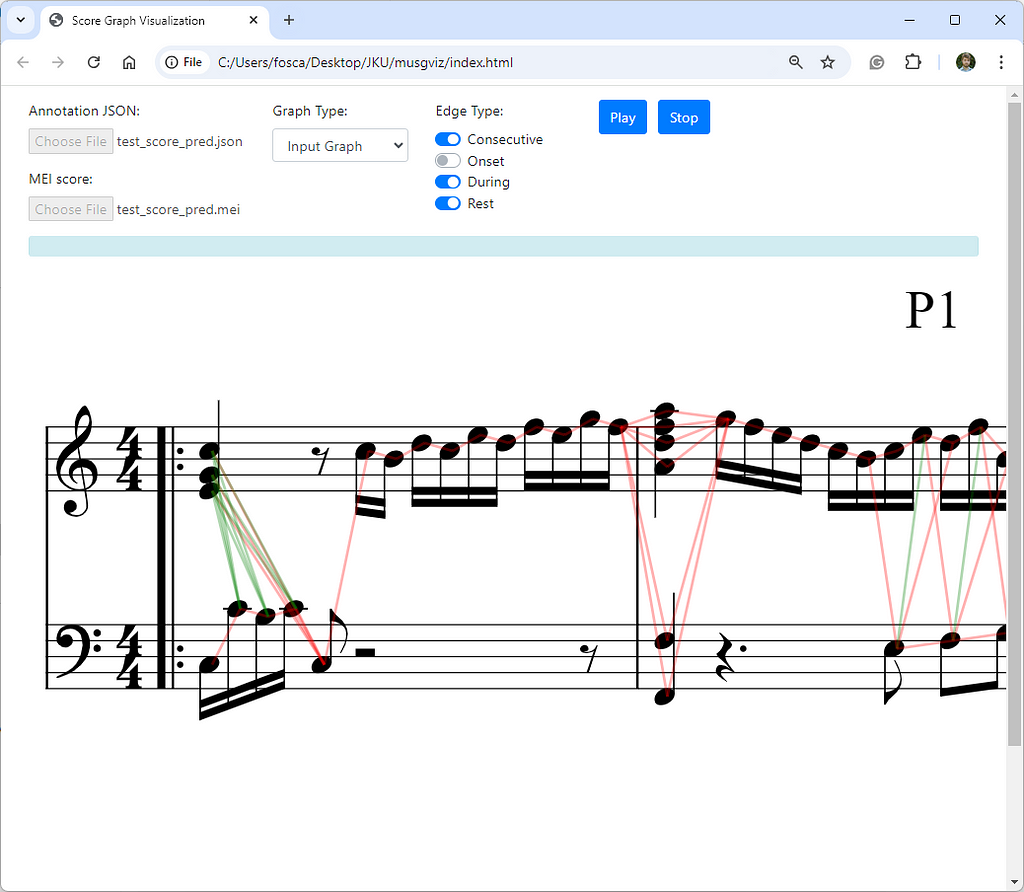
In the interest of giving a fair comparison and deeper understanding of how our model works and how the predictions can vary, we take a closer look at some.
We compare the ground truth edges (links) to our predicted edges for chord and voice prediction. Note that in the example you are viewing below the output graph is plotted directly on top of the score with the help of our visualization tool.
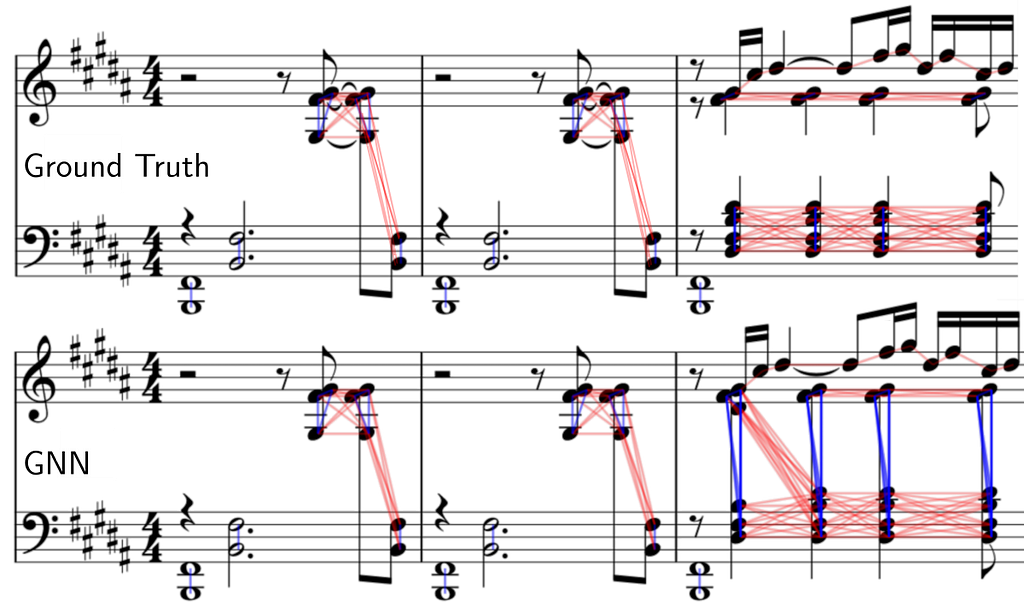
The first two bars are done perfectly, however we can see some limitations of our system at the third bar. Synchronous notes within a close pitch range but with a different voice arrangement can be problematic.
Our model predicts a single chord (instead of splitting across the staff) containing all the synchronous syncopated quarter notes and also mispredicts the staff for the first D#4 note. A more in-depth study of why this happens is not trivial, as neural networks are not directly interpretable.
Open Challenges
Despite the strengths of our system, several challenges remain open for future development. Currently, grace notes are not accounted for in this version, and overlapping notes must be explicitly duplicated in the input, which can be troublesome. Additionally, while we have developed an initial MEI export feature for visualizing the results, this still requires further updates to fully support the various exceptions and complexities found in symbolic scores. Addressing these issues will be key to enhancing the system’s versatility and making it more adaptable to diverse musical compositions.
Conclusion
This blog presented a graph-based method for homophonic voice separation and staff prediction in symbolic piano music. The new approach performs better than existing deep-learning or heuristic-based systems. Finally, it includes a post-processing step that can remove problematic predictions from the model that could result in incorrect scores.
[all images are by the author]
Voice and Staff Separation in Symbolic Piano Music with GNNs was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Voice and Staff Separation in Symbolic Piano Music with GNNs
Go Here to Read this Fast! Voice and Staff Separation in Symbolic Piano Music with GNNs
