Unveiling Metadynamics: A Beginner’s Guide to Mastering PLUMED (Part 1 of 3)

Unveiling Metadynamics

A beginner’s guide to mastering PLUMED (Part 1 of 3)

In computational chemistry and molecular dynamics (MD), understanding complex systems sometimes requires analysis beyond what is provided by your MD engine or a visualization in VMD. I personally work with atomistic simulations of biological molecules, and they’re pretty friggin’ big. And with the complexity of calculating the trajectories of every atom in those big simulation boxes, typically I don’t get to see trajectories that go beyond 1 or 2 microseconds, which is a consistent upper limit for many MD runs. This means that, while traditional MD is great for seeing fluctuations in your trajectories for processes that occur in less than that amount of time, but what about ones that take longer?

A powerful technique exists to look at these processes called metadynamics, and PLUMED stands out as a leading tool in this domain due to its seamless integration with the GROMACS engine. In this series of articles, we will build up an understanding of metadynamics, both in terms of theory, code, and syntax, with the end goal of being able to generate complex metadynamics simulations for whatever you’re trying to get a better look at! This article specifically will be an introduction to the concepts and some general code for properly installing PLUMED and a quick run.

This article assumes the reader is already familiar with some Molecular Dynamics (MD) engine and can generate a system for that engine. This isn’t necessary if you’re just looking to learn about a cool technique, but I recommend getting somewhat familiar with an MD engine (my preference is GROMACS) if you’re looking to implement metadynamics.

What is Metadynamics?

Metadynamics is an advanced sampling method designed to explore free energy landscapes of molecular systems. It helps to study rare events and slow processes by encouraging those events over the ones the system is comfortably doing.

It manages to do this by adding a history-dependent bias potential that allows the system to leave local minima in CV space and overcome energy barriers to explore a wider variety of configurations specific to what you’re looking to do.

Understanding Gaussian Distributions in Metadynamics

So the key to the success of metadynamics is the implementation of targeted Gaussian distributions in the relative free energy of the system. To understand this process, let’s take a look at the classical physics trope of a ball on a hill. We all know the ball rolls down, but what if the hill isn’t just a hyperbolic hump but a mountain range? Well the ball will still roll down, but it’s likely to get itself trapped in a crevice or come to rest in a flatter area rather than go to the global lowest point in the mountain range.

Metadynamics modifies this scenario by sequentially adding Gaussian kernels, like small mounds of dirt, under the ball. When you add enough dirt over the ball, it’ll be in a position to keep rolling again. We basically do this until we’ve more-or-less filled up the valleys with dirt, and we keep track of every mound of dirt we add. Once we’ve added enough dirt to get a flat surface instead of a mountain range, we can determine the depth of each area by counting up how many mounds we’ve added along with the size of each mound, and we can figure out from that where the lowest-energy spot in the mountain range was.

Now this may not be the most efficient way of doing things with a real ball in a real mountain range; it’s not cost effective or environmentally friendly, and you ruined a mountain range in the process. But if we apply that idea to the free energy surface of a system, it becomes a very desirable option. If we replace the position of the ball with collective variable(s) (CVs) that we’re interested in and perform the same basic task within it, adding Gaussian distributions as we go, we can form a Free Energy Surface (FES) that tells us the relative Gibbs free energy of different conformations of our system, like the one below:

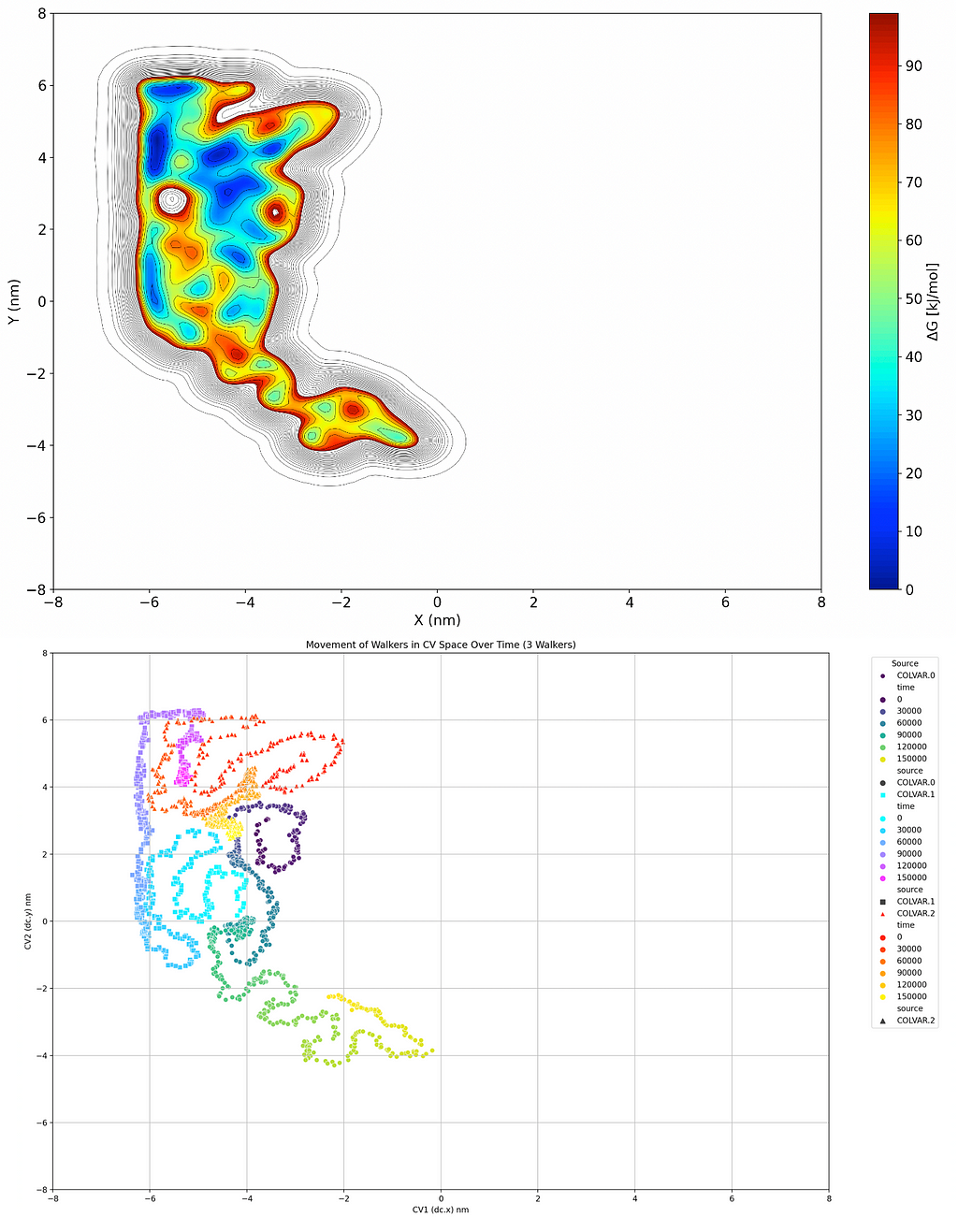
So I’ve included two graphical analyses of a theoretical metadynamics simulation above. The first graph is the one we just discussed, building a topological map of the relative free energies of the system being in a certain state using 2 CVs. I’ve made things easier here by just making the two dimensions spatial, so we’re looking at the position of a molecule relative to point (0, 0) and the energy associated with that. The second one aims to simplify that point by showing a trace of where the molecule has traveled in that coordinate space over time, with coloration to indicate at what time it was in what area. Basically it’s a path that the ball rolled, and if there’s a big clump of points somewhere it’s likely that it corresponds to a minimum on the FES graph. Now a quick point I need to make here is that this was a Multiple Walker (MW) simulation because I just grabbed one quickly from my archives; what that means is that I had three balls rolling and was adding dirt for all three that remained there for all three. We’ll talk about why this is done in a future article, but in case you took a really close look at that graph, that’s why there are 3 separate traces.

Remember, while I’ve used spatial dimensions to more effectively explain the analogy, the CV axes of this graph could be almost anything you can algorithmically explain to PLUMED including torsion, angles, vectors, etc. Visualizing it like a topographical map is just an easy way of understanding how the CVs work and/or work together.

Okay so what up with all the dirt we’re adding? What is a Gaussian Distribution?

A Gaussian distribution (the kernels added), also known as a normal distribution, is a bell-shaped curve characterized by its mean (μ) and standard deviation (σ).

The mathematical representation of a Gaussian distribution is given by the equation:

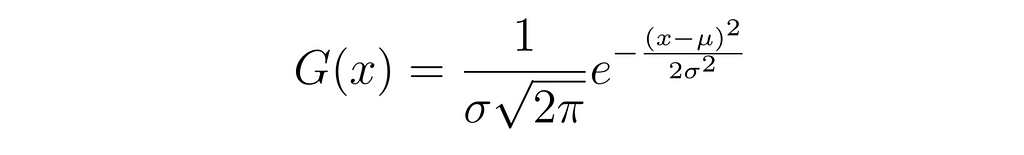
In the context of metadynamics, Gaussian hills are added to the free energy surface at regular intervals (usually) to prevent the system from revisiting previously explored states. These hills are described by Gaussian functions centered at the current position of the system in the collective variable (CV) space. The height and width of these Gaussians determine the influence of the bias.

The equation for a Gaussian hill in metadynamics is:

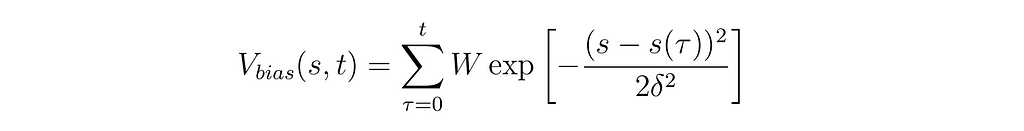
In which s(τ) is the position in CV space at time point τ, W is the height of the Gaussian bias deposit, δ is the width of the deposit, and the sum runs across all times τ where a deposit was added. Basically a fancy way of saying “We added this much dirt in these places”. I’ll delve more into the math behind metadynamics in Part 2 of this article series, so don’t feel like these equations need to make sense to you yet, just knowing about the ball on the hill is plenty for running and analyzing our first metadynamics simulation.

Getting Started with PLUMED

Installation:

Not gonna lie, this gets a little annoying, it needs to be patched into your MD engine. If you’re not interested in GROMACS as your MD engine, here’s a link to the plumed main page because you’re on your own regarding installation:

PLUMED: Installation

Otherwise, here’s how to install them both and properly patch them. Follow all of these commands if you have neither but ignore the GROMACS installation if you already have it installed and working. These commands should be executed one-by-one in your terminal/command line.

#Download GROMACS
wget http://ftp.gromacs.org/pub/gromacs/gromacs-2021.2.tar.gz
tar xfz gromacs-2021.2.tar.gz
cd gromacs-2021.2

#Install and source GROMACS
mkdir build
cd build
cmake .. -DGMX_BUILD_OWN_FFTW=ON -DREGRESSIONTEST_DOWNLOAD=ON
make
sudo make install
source /usr/local/gromacs/bin/GMXRC

#Download PLUMED
wget https://github.com/plumed/plumed2/releases/download/v2.7.1/plumed-2.7.1.tgz
tar xfz plumed-2.7.1.tgz
cd plumed-2.7.1

#install PLUMED
./configure --prefix=/usr/local/plumed
make
sudo make install

#Patch GROMACS
cd gromacs-2021.2
plumed patch -p

#rebuilld GROMACS
cd build
cmake .. -DGMX_BUILD_OWN_FFTW=ON -DREGRESSIONTEST_DOWNLOAD=ON -DGMX_PLUMED=on
make
sudo make install

#Check installation
gmx mdrun -plumed

You’ll notice I’ve picked an older version of gromacs; this is just to give us a better chance that there are no unforseen bugs moving through these articles, you’re more than welcome to use a more recent version at your discretion, just make sure that it’s PLUMED-compatible.

Basic Configuration:

• Create a PLUMED input file to define the collective variables (CVs) that describe the system’s important degrees of freedom.

Here’s an example file. I’ll go into more detail on some fancier options in Part 3 of this article series, but for now we’ll start by looking at the conformational state of a set of atoms by using distance and torsion as our CVs. Other potential CVs include distances between atoms, angles, dihedrals, or more complex functions.

# Define collective variables
# Distance between atoms 1 and 10
DISTANCE ATOMS=1,10 LABEL=d1

# Dihedral angle involving atoms 4, 6, 8, and 10
TORSION ATOMS=4,6,8,10 LABEL=t1

# Print collective variables to a file
PRINT ARG=d1,t1 FILE=COLVAR STRIDE=100

# Apply metadynamics bias
METAD ...
  ARG=d1,t1         # The collective variables to bias
  PACE=500          # Add a Gaussian hill every 500 steps
  HEIGHT=0.3        # Height of the Gaussian hill
  SIGMA=0.1,0.1     # Width of the Gaussian hill for each CV
  FILE=HILLS        # File to store the hills
  BIASFACTOR=10     # Bias factor for well-tempered metadynamics
  TEMP=300          # Temperature in Kelvin
... METAD

# Print the bias potential to a file
PRINT ARG=d1,t1,bias FILE=BIAS STRIDE=500

The comments in that code block should be extensive enough for a basic understanding of everything going on, but I’ll get to all of this in article 3, and we’ll even delve beyond into complex functions!

Anyway, once you have this input file (typically named plumed.dat) and the .tpr file required for an MD run using GROMACS (look at gmx grompp documentation for generating that file), you can run the metadynamics simulation by going to the working directory and typing into the command line:

gmx mdrun -s topol.tpr -plumed plumed.dat

Both PLUMED and GROMACS accept extra arguments. I’ll go over some of the more useful ones for both in Part 3 of this series of articles along with some of the scripts I’ve written for more advanced runs, and you can look at the documentation for any others.

After the simulation, use PLUMED’s analysis tools to reconstruct the free energy surface and identify relevant metastable states and transition pathways. Most ubiquitous is the use of PLUMED’s sum_hills tool to reconstruct the free energy surface.

You can take a look at the free energy surface (FES) after that command using this python code which will tell you how values of one CV relate to the other.

import matplotlib.pyplot as plt
import numpy as np
import plumed
from matplotlib import cm, ticker

# Configure font
plt.rc('font', weight='normal', size=14)

# Read data from PLUMED output
data = plumed.read_as_pandas("/path/to/COLVAR")

# Extract and reshape data for contour plot
# Adjust the reshape parameters as needed, They should multiply to the
# number of bins and be as close to each other as possible
d1 = data["d1"].values.reshape(-1, 100)
t1 = data["t1"].values.reshape(-1, 100)  
bias = data["bias"].values.reshape(-1, 100)

# Plot contour lines
plt.contour(d1, t1, bias, levels=np.arange(np.min(bias), np.max(bias), 10), linewidths=0.3, colors='k')

# Plot filled contour
cntr = plt.contourf(d1, t1, bias, levels=np.arange(0, 100), cmap=cm.jet)

# Add colorbar
plt.colorbar(cntr, label="u0394G [kJ/mol]")

# Set plot limits and labels
plt.xlim(np.min(d1), np.max(d1))
plt.ylim(np.min(t1), np.max(t1))
plt.xlabel("Distance between atoms 1 and 10 (d1) [nm]")
plt.ylabel("Dihedral angle involving atoms 4, 6, 8, and 10 (t1) [degrees]")

# Show plot
plt.show()

The output should look similar to the topographical graph I posted earlier on (I can’t give you what your FESwill look like because you had the freedom of choosing your own system).

You should also visualize the results using popular visualization software like VMD to gain insights into the molecular behavior in low energy and metastable states.

Conclusion

Metadynamics, powered by PLUMED, offers a robust framework for exploring complex molecular systems. By efficiently sampling the free energy landscape, we can uncover hidden mechanisms in molecular systems that can’t be achieved through traditional MD due to computational constraints.

Whether you are a novice or an experienced researcher, mastering PLUMED can significantly enhance your computational chemistry toolkit, so don’t forget to check out my upcoming two articles to help you go from beginner to expert!

Article 2 will unveil the mathematical concepts behind adding metadynamics components to an MD engine, and Article 3 will expose you to advanced techniques in metadynamics such as multiple walker metadynamics, condensing more than 2 variables into a readable format, utilizing metadynamics on high-performance clusters, and more in-depth analytical techniques to visualize and quantitatively analyze your system results (with plenty of sample code).

Unveiling Metadynamics: A Beginner’s Guide to Mastering PLUMED (Part 1 of 3) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.