Unleashing the Power of Triton: Mastering GPU Kernel Optimization in Python

Accelerating AI/ML Model Training with Custom Operators — Part 2

According to Greek mythology, Triton, a god of the sea, would calm or stir the sea waters by using his conch shell to control its tides and waves. In one story, in particular, Triton is depicted as having used his powers to guide the Argonauts through particularly dangerous sea waters. In this post, we similarly call upon Triton for navigation through complex journeys, although this time we refer to the Triton language and compiler for writing deep learning (DL) kernels and to our journeys through the world of AI/ML development.

This is a sequel to a previous post on the topic of accelerating AI/ML applications with custom operators in which we demonstrated the potential for performance optimization by developing custom CUDA kernels. One of our intentions was to emphasize the accessibility of custom kernel development and the opportunities it provides even for non-expert CUDA developers. However, there are challenges to CUDA development that may prove insurmountable for some. For one, while many a modern-day AI/ML developer are well-versed in Python, they may not feel comfortable developing in C++. Furthermore, tuning a CUDA kernel to take full advantage of the GPU’s capabilities requires an intimate understanding of the underlying HW architecture and could take a non-trivial amount of work. This is particularly true if you want your kernel to run optimally on a variety of GPU architectures. Much of the complexity results from CUDA’s “thread-based” development model in which the developer is responsible for designing and optimizing all elements of the GPU kernel threads, including all details related to the use of GPU memory, thread-concurrency, TensorCore scheduling, and much more.

The Power of Triton

The Triton library aims to democratize and simplify GPU kernel development in two primary ways. First, it provides an API for building custom operators in Python (rather than C++). Second, it enables kernel development at the block level (rather than the thread level) thereby abstracting away and automating all issues related to optimizing performance within CUDA thread blocks. Rather than taking the laborious steps of programming the details of the thread invocation, including the intricacies related to memory management, scheduling of on-chip acceleration engines, thread-synchronization, etc., kernel developers can rely on Triton to do it all for them. One important byproduct of the high-level API abstraction of Triton’s programming model is that it reduces the burden of needing to tune the kernel for multiple different GPU types and architectures.

Of course, as is usually the case when up-leveling an API, the Triton programming model does have its disadvantages. Some kernels might benefit from the thread-level control enabled by CUDA (e.g., they might benefit from the conditional execution flow discussed in our previous post). Other kernels might require very specialized and delicate treatment to reach peak performance and may suffer from the automated result of the Triton compiler. But even in cases such as these, where the development of a CUDA kernel may ultimately be required, the ability to quickly and easily create a temporary Triton kernel could greatly facilitate development and boost productivity.

For more on the motivations behind Triton and on the details of its programming model, see the Triton announcement, the official Triton documentation, and the original Triton white-paper.

Disclaimers

Similar to our previous post, our intention is to provide a simple demonstration of the opportunity offered by Triton. Please do not view this post as a replacement for the official Triton documentation or its associated tutorials. We will use the same face-detection model as in our previous post as a basis for our demonstration and perform our experiments in the same Google Cloud environment — a g2-standard-16 VM (with a single L4 GPU) with a dedicated deep learning VM image and PyTorch 2.4.0. As before, we make no effort to optimize our examples and/or verify their robustness, durability, or accuracy. It should be noted that although we will perform our experiments on a PyTorch model and on an NVIDIA GPU, Triton kernel development is supported by additional frameworks and underlying HWs.

Triton as a Component of Torch Compilation

In previous posts (e.g., here) we demonstrated the use of PyTorch compilation and its potential impact on runtime performance. The default compiler used by the torch.compiler is TorchInductor which relies heavily on Triton kernels for its GPU acceleration. Thus, it seems only appropriate that we begin our Triton exploration by assessing the automatic Triton-backed optimization afforded by torch.compile. The code block below includes the same forward pass of the face detection model we introduced in our previous post along with the compiled GIOU loss function. For the sake of brevity, we have omitted some of the supporting code. Please refer to our previous post for the full implementation.

def loss_with_padding(pred, targets):
    mask = (targets[...,3] > 0).to(pred.dtype)
    total_boxes = mask.sum()
    loss = generalized_box_iou(targets, pred)
    masked_loss = loss*mask
    loss_sum = masked_loss.sum()
    return loss_sum/torch.clamp(total_boxes, 1)


device = torch.device("cuda:0")
model = torch.compile(Net()).to(device).train()
loss_fn = torch.compile(loss_with_padding)

# forward portion of training loop wrapped with profiler object
with torch.profiler.profile(
   schedule=torch.profiler.schedule(wait=5, warmup=5, active=10, repeat=1)
) as prof:
    for step, data in enumerate(train_loader):

        with torch.profiler.record_function('copy data'):
            images, boxes = data_to_device(data, device)
            torch.cuda.synchronize(device)

        with torch.profiler.record_function('forward'):
            with torch.autocast(device_type='cuda', dtype=torch.bfloat16):
                outputs = model(images)
            torch.cuda.synchronize(device)

        with torch.profiler.record_function('calc loss'):
            loss = loss_fn(outputs, boxes)
            torch.cuda.synchronize(device)
        prof.step()
        if step > 30:
            break

    # filter and print profiler results
    event_list = prof.key_averages()
    for i in range(len(event_list) - 1, -1, -1):
        if event_list[i].key not in ['forward', 'calc loss', 'copy data']:
            del event_list[i]
    print(event_list.table())

The performance results (averaged over multiple runs) are captured below:

-------------  ------------  ------------
         Name     CPU total  CPU time avg
-------------  ------------  ------------
    copy data      56.868ms       5.687ms
      forward        1.329s     132.878ms
    calc loss       8.282ms     828.159us
-------------  ------------  ------------

Recall that the average time of the original loss function (on padded input) was 1.844ms. Thus the performance boost resulting from torch compilation is greater than 2X(!!).

The Triton kernels automatically generated by torch.compile can actually be viewed by setting the TORCH_LOGS environment variable, as explained in this PyTorch tutorial. In fact, some have proposed the use of these kernels as a starting point for Triton development (e.g., see here). However, in our experience these kernels can be somewhat difficult to decipher.

In the next section we will attempt to further improve on the results of PyTorch compilation by implementing a GIOU Triton kernel.

Creating a Custom Triton Kernel

A great place to start your Triton development journey is with the official Triton tutorials. The tutorials are introduced in incremental order of complexity, with each one expanding on one or more of Triton’s unique features. Our GIOU Triton kernel most closely resembles the most basic vector addition example. As in our CUDA implementation, we assign a block to each sample in the input batch, and program it to operate on all of the bounding boxes in the sample. Note the use of tl.load and tl.store for reading and writing data from and to memory, as well as the block programs use of vectorized arithmetic.

import triton
import triton.language as tl

@triton.jit
def giou_kernel(preds_ptr,
                    targets_ptr,
                    output_ptr,
                    valid_ptr,
                    BLOCK_SIZE: tl.constexpr):
    pid = tl.program_id(axis=0)
    box_id = tl.arange(0, BLOCK_SIZE)
    
    box_offsets = pid * BLOCK_SIZE + box_id
    
    preds_left = tl.load(preds_ptr + 0 + 4 * box_offsets)
    preds_top = tl.load(preds_ptr + 1 + 4 * box_offsets)
    preds_right = tl.load(preds_ptr + 2 + 4 * box_offsets)
    preds_bottom = tl.load(preds_ptr + 3 + 4 * box_offsets)
    
    gt_left = tl.load(targets_ptr + 0 + 4 * box_offsets)
    gt_top = tl.load(targets_ptr + 1 + 4 * box_offsets)
    gt_right = tl.load(targets_ptr + 2 + 4 * box_offsets)
    gt_bottom = tl.load(targets_ptr + 3 + 4 * box_offsets)
    
    epsilon = 1e-5
    
    # Compute the area of each box
    area1 = (preds_right - preds_left) * (preds_bottom - preds_top)
    area2 = (gt_right - gt_left) * (gt_bottom - gt_top)
    
    # Compute the intersection
    left = tl.maximum(preds_left, gt_left)
    top = tl.maximum(preds_top, gt_top)
    right = tl.minimum(preds_right, gt_right)
    bottom = tl.minimum(preds_bottom, gt_bottom)
    
    inter_w = right - left
    inter_h = bottom - top
    inter_area = inter_w * inter_h
    
    union_area = area1 + area2 - inter_area
    
    iou_val = inter_area / tl.maximum(union_area, epsilon)
    
    # Compute the smallest enclosing box
    enclose_left = tl.minimum(preds_left, gt_left)
    enclose_top = tl.minimum(preds_top, gt_top)
    enclose_right = tl.maximum(preds_right, gt_right)
    enclose_bottom = tl.maximum(preds_bottom, gt_bottom)
    
    enclose_w = enclose_right - enclose_left
    enclose_h = enclose_bottom - enclose_top
    enclose_area = enclose_w * enclose_h
    
    # Compute GIOU
    delta_area = (enclose_area - union_area)
    enclose_area = tl.maximum(enclose_area, epsilon)
    giou = iou_val - delta_area / enclose_area
    
    # Store results
    tl.store(output_ptr + (box_offsets),
             tl.where(gt_bottom > 0, giou, 0))
    tl.store(valid_ptr + (box_offsets), gt_bottom > 0)


def loss_with_triton(pred, targets):
    batch_size = pred.shape[0]
    n_boxes = pred.shape[1]
    
    # convert to float32 (remove to keep original dtypes)
    pred = pred.to(torch.float32)
    targets = targets.to(torch.float32)

    # allocate output tensors
    output = torch.empty_strided(pred.shape[0:2], 
                                 stride=(n_boxes,1),
                                 dtype = pred.dtype,
                                 device = pred.device)
    valid = torch.empty_strided(pred.shape[0:2],
                                stride=(n_boxes,1),
                                dtype = torch.bool,
                                device = pred.device)
 
    # call Triton kernel
    giou_kernel[(batch_size,)](pred, targets, output, valid,
                               BLOCK_SIZE=n_boxes)

    total_valid = valid.sum()
    loss_sum = output.sum()
    return loss_sum/total_valid.clamp(1)

The results of running with our Triton kernel are captured below. While somewhat worse than in our previous experiment, this could be a result of additional optimizations performed by torch.compile.

-------------  ------------  ------------
         Name     CPU total  CPU time avg
-------------  ------------  ------------
    copy data      57.089ms       5.709ms
      forward        1.338s     133.771ms
    calc loss       8.908ms     890.772us
-------------  ------------  ------------

Following the recommendation of PyTorch’s documentation on the use of Triton kernels, we further assess the performance of our kernel, this time in combination with PyTorch compilation. The results (averaged over multiple runs) are slightly better than the auto-compiled loss of our first experiment.

-------------  ------------  ------------
         Name     CPU total  CPU time avg
-------------  ------------  ------------
    copy data      57.008ms       5.701ms
      forward        1.330s     132.951ms
    calc loss       7.189ms     718.869us
-------------  ------------  ------------

When developing our custom GIOU CUDA kernel, we noted the overhead of converting the input tensors to float32, and the need to enhance our kernel to support various input types in order to avoid this conversion. In the case of our Triton kernel this can be accomplished quite easily by simply removing the conversion operations. The custom kernel will be auto-generated (JIT-compiled) with the original types.

-------------  ------------  ------------
         Name     CPU total  CPU time avg
-------------  ------------  ------------
    copy data      57.034ms       5.703ms
      forward        1.325s     132.456ms
    calc loss       6.219ms     621.950us
-------------  ------------  ------------

Our final results are on par with CUDA kernel results that we saw in our previous post.

Results

The following table summarizes the results of our experimentation. The results were averaged over multiple runs due to some variance that we observed. We have included the results of our custom CUDA kernel from our previous post, for reference. Keep in mind that the comparative results are likely to vary greatly based on the details of the kernel and the runtime environment.

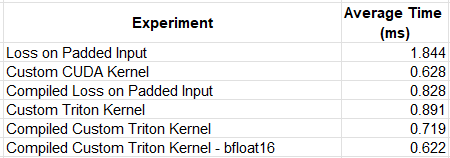
While our first Triton kernel experiment resulted in reduced performance, compared to our custom CUDA operator, by applying compilation and removing the data type conversions, we were able to match its speed.

These findings are in line with what one might expect from Triton: On the one hand, its high-level API abstraction implies a certain loss of control over the low-level flow which could result in reduced runtime performance. On the other hand, the (relative) simplicity and power of its APIs enable users to close the performance gap by implementing features with much greater ease than in CUDA.

One could make a strong argument that the Triton kernel we chose to evaluate is what the documentation would refer to as “embarrassingly parallel”, i.e., comprised of element-wise operations, and that as such, is a terrible kernel on which to demonstrate the value of Triton. Indeed, a more complex program, requiring more sophisticated memory management, scheduling, synchronization, etc., may be required to showcase the full power of Triton.

Next Steps

Several additional steps are required to complete our task. These include tuning our custom kernel and implementing the backward function.

1. Kernel Optimization

Although, Triton abstracts away a lot of the low-level kernel optimization, there remain many controls that could greatly impact runtime performance. These include the size of each block, the number of thread warps to use (as demonstrated in the softmax tutorial), and how L2 memory is accessed (see the matrix multiplication tutorial for an example of swizzling). Triton includes an autotuning feature for optimizing the choice of hyper-parameters (as demonstrated in the matrix multiplication tutorial and in the PyTorch Triton example). Although we have omitted autotuning from our example, it is an essential step of Triton kernel development.

2. Backward Pass Implementation

We have limited our example to just the forward pass of the GIOU loss function. A full solution would require creating a kernel for the backward pass, as well (as demonstrated in the layer normalization tutorial). This is usually a bit more complicated than the forward pass. One may wonder why the high-level kernel development API exposed by Triton does not address this challenge by supporting automatic differentiation. As it turns out, for reasons that are beyond the scope of this post (e.g., see here), automatic differentiation of custom kernels is extremely difficult to implement. Nonetheless, this would be an absolute killer of a feature for Triton and we can only hope that this will be supported at some point in the future.

Summary

Triton is easily one of the most important and impactful AI/ML libraries of the past few years. While it is difficult to assess the amount of innovation and progress it has enabled in the field of AI, its footprints can be found everywhere — from the core implementation of PyTorch 2 and its dependencies, to the specialized attention layers within the advanced LLM models that are slowly perforating our every day lives.

Triton’s popularity is owed to its innovative programming model for kernel development. Once limited to the domain of CUDA experts, Triton makes creating customized DL primitives accessible to every Python developer.

In this post we have only touched the surface of Triton and its capabilities. Be sure to check out the Triton’s online documentation and other resources to learn more.

Unleashing the Power of Triton: Mastering GPU Kernel Optimization in Python was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.