Towards Reliable Synthetic Control

Making the estimated treatment effect close to the truth

Introduction

In recent years, the Synthetic Control (SC) approach has gained increasing adoption in industry for measuring the the Average Treatment Effect (ATE) of interventions when Randomized Control Trials (RCTs) are not available. One such example is measuring the financial impact of outdoor advertisements on billboards whereby we cannot conduct random treatment assignment in practice.

The basic idea of SC is to estimate ATE by comparing the treatment group against the predicted counterfactual. However, applying SC in practice is usually challenged by the limited knowledge of its validity due to the absence of the true counterfactual in the real world. To mitigate the concern, in this article, I would like to discuss the actionable best practices that help to maximise the reliability of the SC estimation.

The insights and conclusions are obtained through experiments based on diverse synthetic data. The code for data generation, causal inference modeling, and analysis is available in the Jupyter notebook hosted on Github.

Synthetic Control in a Nutshell

The key to measure the ATE of such events is to identify the counterfactual of the treatment group, which is the treatment group in the absence of the treatment, and quantify the post-treatment difference between the two. It is simple for RCTs as the randomised control statistically approximates the counterfactual. However, it’s challenging otherwise due to the unequal pre-experiment statistics between the treatment and control.

As a causal inference technique, SC represents the counterfactual by a synthetic control group created based on some untreated control units. This synthetic control group statistically equals the treatment group pre treatment and is expected to approximate the untreated behaviour of the treatment group post treatment. Mathematically presented below, it is created using the function f whose parameters are obtained by minimising the pre-treatment difference between the treated group and the control synthesised by f [1]:

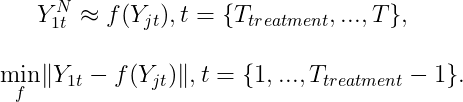
In practice, the popular options for the function f include but are not limited to the weighted sum [1], Bayesian Structural Time Series (BSTS) [2], etc.

Actions towards Reliable Synthetic Control

Despite the solid theoretical foundation, applying SC in practice usually faces the challenge that we don’t know how accurate the estimated ATE is because there exists no post-treatment counterfactual in reality to validate the synthesised one. However, there are some actions we can take to optimise the modeling process and maximise the reliability. Next, I will describe these actions and demonstrate how they influence the estimated ATE via a range of experiments based on the synthetic time-series data with diverse temporal characteristics.

Experiment Setup

All the experiments presented in this article are based on synthetic time-series data. These data are generated using the timeseries-generator package that produces time series capturing the real-world factors including GDP, holidays, weekends, and so on.

GitHub – Nike-Inc/timeseries-generator: A library to generate synthetic time series data by easy-to-use factors and generator

The data generation aims to simulate the campaign performance of the stores in New Zealand from 01/01/2019 to 31/12/2019. To make the potential conclusions statistically significant, 500 time series are generated to represent the stores. Each time series has the statistically randomised linear trend, white noise, store factor, holiday factor, weekday factor, and seasonality. A random sample of 10 stores are presented below.

Store1 is selected to be the treatment group whereas others play the role of control groups. Next, the outcome of store1 is uplifted by 20% from 2019-09-01 onwards to simulate the treated behaviour whereas its original outcome serves as the real counterfactual. This 20% uplift establishes the actual ATE to validate the actions later on.

cutoff_date_sc = '2019-09-01'
df_sc.loc[cutoff_date_sc:] = df_sc.loc[cutoff_date_sc:]*1.2

The figure below visualises the simulated treatment effect and the true counterfactual of the treatment group.

Given the synthetic data, the BSTS in Causalimpact is adopted to estimate the synthesised ATE. Then, the estimation is compared against the actual ATE using Mean Absolute Percentage Error (MAPE) to evaluate the corresponding action.

GitHub – jamalsenouci/causalimpact: Python port of CausalImpact R library

Next, let’s go through the actions along with the related experiments to see how to produce reliable ATE estimation.

Treatment-control Correlation

The first action to achieve reliable ATE estimation is selecting the control groups that exhibit high pre-treatment correlations with the treatment group. The rationale is that a highly correlated control is likely to consistently resemble the untreated treatment group over time.

To validate this hypothesis, let’s evaluate the ATE estimation produced using every single control with its full data since 01/01/2019 to understand the impact of correlation. Firstly, the correlation coefficients between the treatment group (store1) and the control groups (store2 to 499) are calculated [3].

def correlation(x, y):
    shortest = min(x.shape[0], y.shape[0])
    return np.corrcoef(x.iloc[:shortest].values, y.iloc[:shortest].values)[0, 1]

As shown in the figure below, the distribution of the correlations range from -0.1 to 0.9, which provides a comprehensive understanding about the impact across various scenarios.

Then, every individual control is used to predict the counterfactual, estimate the ATE, and report the MAPE. In the figure below, the averaged MAPE of ATE with its 95% confidence interval is plotted against the corresponding pre-treatment correlation. Here, the correlation coefficients are rounded to one decimal place to facilitate aggregation and improve the statistical significance in the analysis. Looking at the results, it is obvious that the estimation shows a higher reliability when the control gets more correlated with the treatment group.

Now let’s see some examples that demonstrate the impact of pre-treatment correlation: store88 with a correlation of 0.88 delivers a MAPE of 0.12 that is superior to 0.62 given by store3 with a correlation of 0.43. Besides the promising accuracy, the probabilistic intervals are correspondingly narrow, which implies high prediction certainty.

Model Fitting Window

Next, the fitting window, which is the length of the pre-treatment interval used for fitting the model, needs to be properly configured. This is because too much context could result in a loss of recency while insufficient context might lead to overfitting.

To understand how fitting window impacts the accuracy of ATE estimation, a wide range of values from 1 month to 8 months before the treatment date are experimented. For each fitting window, every single unit of the 499 control groups is evaluated individually and then aggregated to calculate the averaged MAPE with the 95% confidence interval. As depicted in the figure below, there exists a sweet spot nearby 2 and 3 months that optimise the reliability. Identifying the optimal point is outside the scope of this discussion but it’s worth noting that the training window needs to be carefully selected.

The figure shows two examples: the MAPE of control group 199 is reduced from 0.89 to 0.68 when its fitting window is increased from 1 month to 3 months because the short window contains insufficient knowledge to produce the counterfactual.

Number of Control Units

Lastly, the number of the selected control groups matters.

This hypothesis is validated by investigating the estimation accuracy for different numbers of controls ranging from 1 to 10. In detail, for each control count, the averaged MAPE is calculated based on the estimations produced by 50 random control sets with each containing the corresponding number of control groups. This operation avoids unnecessarily enumerating every possible combination of controls while statistically controls for correlation. In addition, the fitting window is set to 3 months for every estimation.

Looking at the results below, increasing the number of controls is overall leading towards a more reliable ATE estimation.

The examples below demonstrate the effect. The first estimation is generated using store311 whereas the second one further adds store301 and store312.

Conclusions

In this article, I discussed the possible actions that make the SC estimation more reliable. Based on the experiments with diverse synthetic data, the pre-treatment correlation, fitting window, and number of control units are identified as compelling directions to optimise the estimation. Finding the optimal value for each action is out of the scope of this discussion. However, if you feel interested, parameter search using an isolated blank period for validation [4] is one possible solution.

All the images are produced by the author unless otherwise noted. The discussions are inspired by the great work “Synthetic controls in action” [1].

References

[1] Abadie, Alberto, and Jaume Vives-i-Bastida. “Synthetic controls in action.” arXiv preprint arXiv:2203.06279 (2022).

[2]Brodersen, Kay H., et al. “Inferring causal impact using Bayesian structural time-series models.” (2015): 247–274.

[3]https://medium.com/@dreamferus/how-to-synchronize-time-series-using-cross-correlation-in-python-4c1fd5668c7a

[4]Abadie, Alberto, and Jinglong Zhao. “Synthetic controls for experimental design.” arXiv preprint arXiv:2108.02196 (2021).

Towards Reliable Synthetic Control was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.