Dive into the techniques to fine-tune Neural Networks, understand their mathematics, build them from scratch, and explore their applications

While you might get by in machine learning by trying out a few models, picking the best performer, and tweaking some settings, deep learning doesn’t play by the same rules. If you’ve ever experimented with Neural Networks, you might’ve noticed their performance can be pretty hit or miss. You might even have seen something as straightforward as Logistic Regression beat your fancy 200-layer Deep Neural Network.
Why does this happen? Deep learning is among the most advanced AI techniques we have, but it demands a solid understanding and careful handling. Knowing how to fine-tune a Neural Network, getting what’s going on inside it, and mastering its use are crucial. That’s what we’re diving into today!
Before we jump into the article, I suggest you pull up this Jupyter Notebook. It’s got all the code we’ll be covering today, so having it handy will make it easier to follow along:
Index
· 1: Introduction
∘ 1.1: Elevating Our Basic Neural Network
∘ 1.2: The Path to Complexity
· 2: Expanding Model Complexity
∘ 2.1: Adding More Layers
· 3: Optimization Techniques for Enhanced Learning
∘ 3.1: Learning Rate
∘ 3.2: Early Stopping Techniques
∘ 3.3: Initialization Methods
∘ 3.4: Dropout
∘ 3.5: Gradient Clipping
· 4: Determining the Optimal Number of Layers
∘ 4.1: Layer Depth and Model Performance
∘ 4.2: Strategies for Testing and Selecting the Appropriate Depth
· 5: Automated Fine-Tuning with Optuna
∘ 5.1: Introduction to Optuna
∘ 5.2: Integrating Optuna for Neural Network Optimization
∘ 5.3: Practical Implementation
∘ 5.4: Benefits and Outcomes
∘ 5.5: Limitations
· 6: Conclusion
∘ 6.1: What’s Next
1: Introduction
1.1: Elevating Our Basic Neural Network
In our last dive into artificial intelligence, we built a neural network from the ground up. This basic model opened up the world of neural networks to us — the core of today’s AI tech. We covered the essentials: how input, hidden, and output layers, along with activation functions, come together to process info and make predictions. Then, we put theory into practice with a simple neural network trained on a digits dataset for a computer vision task.
Now, we’re going to build on that foundation. We’ll introduce more complexity by adding layers and exploring various techniques for initialization, regularization, and optimization. And, of course, we’ll put our code to the test to see how these tweaks impact our Neural Network’s performance.
If you haven’t checked out my previous article where we built a neural network from scratch, I recommend giving it a read. We’ll be building on that work, and I’ll assume you’re already familiar with the concepts we covered.
The Math Behind Neural Networks
1.2: The Path to Complexity
Transforming a neural network from a basic setup to a more sophisticated one isn’t just about piling on more layers or nodes. It’s a delicate dance of fine-tuning that requires a solid grasp of the network’s structure and the nuances of the data it handles. As we dive deeper, our goal becomes to enrich our neural network’s depth, layering in more complexity to better discern intricate patterns and connections in the data.
However, beefing up complexity isn’t without its hurdles. With each new layer we introduce, the necessity for refined optimization techniques grows. These are crucial not just for effective learning but also for the model’s ability to adapt to new, unseen data. This guide will walk you through beefing up our foundational neural network. We’ll dive into sophisticated strategies to fine-tune our network, including tweaks to learning rates, adopting early stopping, and playing around with various optimization algorithms like SGD (Stochastic Gradient Descent) and Adam.
We’re also going to cover the significance of how we kick things off with initialization methods, the advantages of using dropout to dodge overfitting, and why keeping our network’s gradients in check with clipping and normalization matters so much for stability. Plus, we’ll tackle the challenge of figuring out the best number of layers to add — enough to enhance learning but not so many that we tip into unnecessary complexity.
Below is the Neural Network and Trainer class we put together in our last article. We’re going to tweak it and practically explore how each modification affects our model’s performance:
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, loss_func='mse'):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.loss_func = loss_func
# Initialize weights and biases
self.weights1 = np.random.randn(self.input_size, self.hidden_size)
self.bias1 = np.zeros((1, self.hidden_size))
self.weights2 = np.random.randn(self.hidden_size, self.output_size)
self.bias2 = np.zeros((1, self.output_size))
# track loss
self.train_loss = []
self.test_loss = []
def __str__(self):
return f"Neural Network Layout:nInput Layer: {self.input_size} neuronsnHidden Layer: {self.hidden_size} neuronsnOutput Layer: {self.output_size} neuronsnLoss Function: {self.loss_func}"
def forward(self, X):
# Perform forward propagation
self.z1 = np.dot(X, self.weights1) + self.bias1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.weights2) + self.bias2
if self.loss_func == 'categorical_crossentropy':
self.a2 = self.softmax(self.z2)
else:
self.a2 = self.sigmoid(self.z2)
return self.a2
def backward(self, X, y, learning_rate):
# Perform backpropagation
m = X.shape[0]
# Calculate gradients
if self.loss_func == 'mse':
self.dz2 = self.a2 - y
elif self.loss_func == 'log_loss':
self.dz2 = -(y/self.a2 - (1-y)/(1-self.a2))
elif self.loss_func == 'categorical_crossentropy':
self.dz2 = self.a2 - y
else:
raise ValueError('Invalid loss function')
self.dw2 = (1 / m) * np.dot(self.a1.T, self.dz2)
self.db2 = (1 / m) * np.sum(self.dz2, axis=0, keepdims=True)
self.dz1 = np.dot(self.dz2, self.weights2.T) * self.sigmoid_derivative(self.a1)
self.dw1 = (1 / m) * np.dot(X.T, self.dz1)
self.db1 = (1 / m) * np.sum(self.dz1, axis=0, keepdims=True)
# Update weights and biases
self.weights2 -= learning_rate * self.dw2
self.bias2 -= learning_rate * self.db2
self.weights1 -= learning_rate * self.dw1
self.bias1 -= learning_rate * self.db1
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
return x * (1 - x)
def softmax(self, x):
exps = np.exp(x - np.max(x, axis=1, keepdims=True))
return exps/np.sum(exps, axis=1, keepdims=True)
class Trainer:
def __init__(self, model, loss_func='mse'):
self.model = model
self.loss_func = loss_func
self.train_loss = []
self.val_loss = []
def calculate_loss(self, y_true, y_pred):
if self.loss_func == 'mse':
return np.mean((y_pred - y_true)**2)
elif self.loss_func == 'log_loss':
return -np.mean(y_true*np.log(y_pred) + (1-y_true)*np.log(1-y_pred))
elif self.loss_func == 'categorical_crossentropy':
return -np.mean(y_true*np.log(y_pred))
else:
raise ValueError('Invalid loss function')
def train(self, X_train, y_train, X_test, y_test, epochs, learning_rate):
for _ in range(epochs):
self.model.forward(X_train)
self.model.backward(X_train, y_train, learning_rate)
train_loss = self.calculate_loss(y_train, self.model.a2)
self.train_loss.append(train_loss)
self.model.forward(X_test)
test_loss = self.calculate_loss(y_test, self.model.a2)
self.val_loss.append(val_loss)
2: Expanding Model Complexity
Diving deeper into refining neural networks, we hit upon a game-changing strategy: dialing up the complexity by layering on more levels. This move isn’t just about bulking up the model; it’s about sharpening its ability to grasp and interpret nuances in the data with greater sophistication.
2.1: Adding More Layers
The Rationale Behind Increased Network Depth
At the heart of deep learning is its knack for piecing together hierarchical data representations. By weaving in more layers, we’re essentially equipping our neural network with the tools to pick apart and understand patterns of growing intricacy. Think of it as teaching the network to start with recognizing simple forms and textures and gradually advancing to unravel more complex relationships and features in the data. This layered learning approach somewhat mirrors how humans make sense of information, evolving from basic understanding to complex interpretation.
Piling on more layers boosts the network’s “learning capacity,” broadening its horizon to map out and digest a more extensive range of data relationships. This enables the handling of more elaborate tasks. But it’s not a free-for-all; adding layers willy-nilly without them meaningfully contributing to the model’s intelligence could muddy the learning process rather than clarify it.
Guide to Integrating More Layers
class NeuralNetwork:
def __init__(self, layers, loss_func='mse'):
self.layers = []
self.loss_func = loss_func
# Initialize layers
for i in range(len(layers) - 1):
self.layers.append({
'weights': np.random.randn(layers[i], layers[i + 1]),
'biases': np.zeros((1, layers[i + 1]))
})
# track loss
self.train_loss = []
self.test_loss = []
def forward(self, X):
self.a = [X]
for layer in self.layers:
self.a.append(self.sigmoid(np.dot(self.a[-1], layer['weights']) + layer['biases']))
return self.a[-1]
def backward(self, X, y, learning_rate):
m = X.shape[0]
self.dz = [self.a[-1] - y]
for i in reversed(range(len(self.layers) - 1)):
self.dz.append(np.dot(self.dz[-1], self.layers[i + 1]['weights'].T) * self.sigmoid_derivative(self.a[i + 1]))
self.dz = self.dz[::-1]
for i in range(len(self.layers)):
self.layers[i]['weights'] -= learning_rate * np.dot(self.a[i].T, self.dz[i]) / m
self.layers[i]['biases'] -= learning_rate * np.sum(self.dz[i], axis=0, keepdims=True) / m
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
return x * (1 - x)
In this section, we’ve made some significant adjustments to how our neural network operates, aiming for a model that flexibly supports any number of layers. Here’s a breakdown of what’s changed:
First off, we’ve dropped the self.input, self.hidden, and self.output variables that previously defined the number of nodes in each layer. Our goal now is a versatile model that can manage an arbitrary number of layers. For instance, to replicate our prior model used on the digits dataset—which had 64 input nodes, 64 hidden nodes, and 10 output nodes—we could simply set it up like this:
nn = NeuralNetwork(layers=[64, 64, 10])
You’ll notice that the code now loops over each layer three times, each for a different purpose:
During initialization, all weights and biases across every layer are set up. This step is crucial for preparing the network with the initial parameters it needs for the learning process.
During the Forward pass, the activations self.a are collected in a list, starting with the activation of the input layer (essentially, the input data X). For every layer, it calculates the weighted sum of inputs and biases using np.dot(self.a[-1], layer[‘weights’]) + layer[‘biases’], applies the sigmoid activation function, and tacks the result onto self.a. The outcome of the network is the last element in self.a, which represents the final output.
During the Backward pass, this stage kicks off by figuring out the derivative of the loss concerning the last layer’s activations (self.dz) and preps the list with the output layer’s error. It then walks back through the network (using reversed(range(len(self.layers) – 1))), calculating error terms for the hidden layers. This involves dotting the current error term with the next layer’s weights (backward) and scaling by the sigmoid function’s derivative to handle the non-linearity.
class Trainer:
...
def train(self, X_train, y_train, X_test, y_test, epochs, learning_rate):
for _ in range(epochs):
self.model.forward(X_train)
self.model.backward(X_train, y_train, learning_rate)
train_loss = self.calculate_loss(y_train, self.model.a[-1])
self.train_loss.append(train_loss)
self.model.forward(X_test)
test_loss = self.calculate_loss(y_test, self.model.a[-1])
self.test_loss.append(test_loss)
Lastly, we’ve updated the Trainer class to align with the changes in the NeuralNetwork class. The significant adjustments are in the train method, particularly in recalculating training and testing loss since the network’s output is now fetched from self.model.a[-1] rather than self.model.a2.
These modifications not only make our neural network more adaptable to different architectures but also underscore the importance of understanding the flow of data and gradients through the network. By streamlining the structure, we enhance our ability to experiment with and optimize the network’s performance across various tasks.
3: Optimization Techniques for Enhanced Learning
Optimizing neural networks is essential for boosting their ability to learn, ensuring efficient training, and steering them toward the best version they can be. Let’s dive into some crucial optimization techniques that significantly impact how well our models perform.
3.1: Learning Rate
The learning rate is the control knob for adjusting the network’s weights based on the loss gradient. It sets the pace at which our model learns, determining how big or small the steps we take during optimization are. Getting the learning rate just right can help the model quickly find a solution with low error. On the flip side, if we don’t set it correctly, we might end up with a model that either takes forever to converge or doesn’t find a good solution at all.
If we set the learning rate too high, our model might just skip right over the best solution, leading to erratic behavior. This can show up as the accuracy or loss swinging wildly during training.
A learning rate that’s too low creeps along too slowly, dragging out the training process. Here, you’ll see the training loss barely budging over time.
The trick is to monitor our training and validation loss as we go, which can give us clues about how our learning rate is doing. Two practical approaches are to log these losses at intervals during training and then plot them afterward to get a clearer picture of how smooth or erratic our loss landscape is. In our code, we’re using Python’s logging library to help us keep tabs on these metrics. Here’s how it looks:
import logging
# Set up the logger
logging.basicConfig(level=logging.INFO)
logger = logging.getLogger(__name__)
class Trainer:
...
def train(self, X_train, y_train, X_val, y_val, epochs, learning_rate):
for epoch in range(epochs):
...
# Log the loss and validation loss every 50 epochs
if epoch % 50 == 0:
logger.info(f'Epoch {epoch}: loss = {train_loss}, val_loss = {val_loss}')
At the start, we set up a logger to capture and display our training updates. This setup allows us to log the training and validation loss every 50 epochs, giving us a steady stream of feedback on how our model is doing. With this feedback, we can start to see patterns — maybe our loss is dropping nicely, or maybe it’s a bit too erratic, hinting that we might need to adjust our learning rate.
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
smooth_train_loss = smooth_curve(trainer.train_loss)
smooth_val_loss = smooth_curve(trainer.val_loss)
plt.plot(smooth_train_loss, label='Smooth Train Loss')
plt.plot(smooth_val_loss, label='Smooth Val Loss')
plt.title('Smooth Train and Val Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
The code above, instead, will allow us to plot training and validation loss to get a better understanding of how the losses behave during the training. Notice that we are adding an smoothing element, as we expect a little bit of noisiness for many iterations. Smoothing the noisiness will help us analyze the graph better.
Following this approach, once we kick off the training, we can expect to see logs pop up, providing a snapshot of our progress and helping us make informed adjustments along the way.
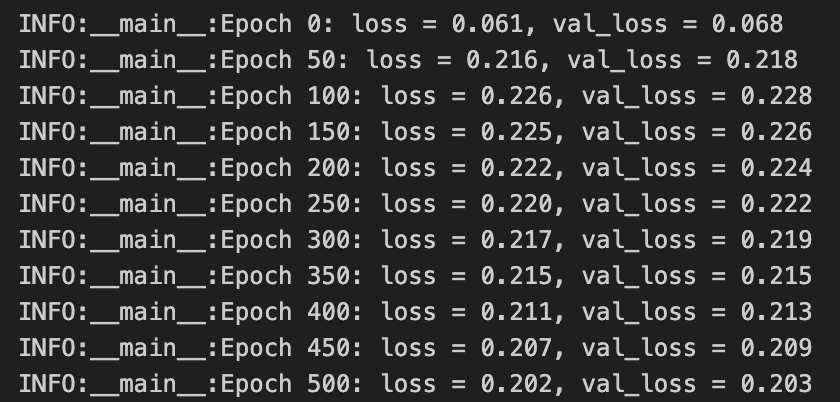
Then, we can plot the losses at the end of the training:
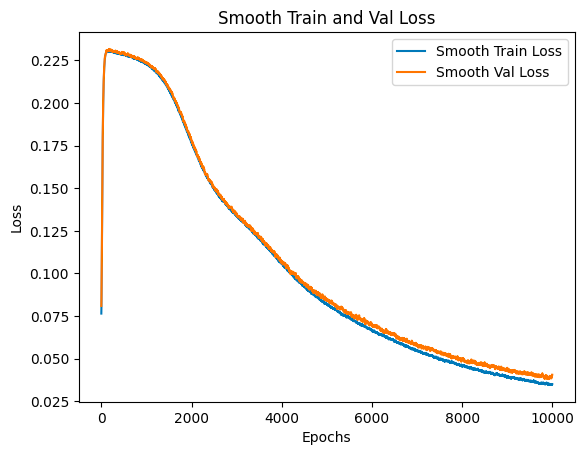
Seeing both training and validation losses steadily decrease is a good sign — it hints that bumping up the number of epochs and perhaps increasing the learning rate’s step size could work well for us. On the flip side, if we spot our losses yo-yo-ing, shooting up after a decrease, it’s a clear signal to dial down the learning rate’s step size. There’s a curious bit, though: between epoch 0 and epoch 50, something odd’s happening with our losses. We’ll circle back to figure that out.
To zero in on that sweet spot for the learning rate, methods like learning rate annealing or adaptive learning rate techniques can be really handy. They fine-tune the learning rate on the fly, helping us stick to an optimal pace throughout the training.
3.2: Early Stopping Techniques
Early stopping is like a safety net — it watches how the model does on a validation set and calls time on training when things aren’t getting any better. This is our guard against overfitting, ensuring our model stays general enough to perform well on data it hasn’t seen before.
Here’s how to put it into action:
- Validation Set: Carve out a slice of your training data to serve as a validation set. This is key because it means our stopping decision is based on fresh, unseen data.
- Monitoring: Keep an eye on how the model fares on the validation set after each training epoch. Is it getting better, or has it plateaued?
- Stopping Criterion: Decide on a rule for when to stop. A common one is “no improvement in validation loss for 50 straight epochs.”
Let’s dive into what the code for this might look like:
class Trainer:
def train(self, X_train, y_train, X_val, y_val, epochs, learning_rate,
early_stopping=True, patience=10):
best_loss = np.inf
epochs_no_improve = 0
for epoch in range(epochs):
...
# Early stopping
if early_stopping:
if val_loss < best_loss:
best_loss = val_loss
best_weights = [layer['weights'] for layer in self.model.layers]
epochs_no_improve = 0
else:
epochs_no_improve += 1
if epochs_no_improve == patience:
print('Early stopping!')
# Restore the best weights
for i, layer in enumerate(self.model.layers):
layer['weights'] = best_weights[i]
break
In the train method, we’ve introduced two new options:
- early_stopping: This is a yes-or-no flag that lets us turn early stopping on or off.
- patience: This sets how many rounds of no improvements in validation loss we’re willing to wait before we call it quits on training.
We kick things off by setting best_loss to infinity. This acts as our benchmark for the lowest validation loss we’ve seen so far during training. Meanwhile, epochs_no_improve keeps a tally of how many epochs have gone by without any betterment in validation loss.
As we loop through each epoch to train our model with the training data, we’re on the lookout for changes in validation loss after every pass (the actual training steps like forward propagation and backpropagation aren’t detailed here but are vital parts of the process).
Post every epoch, we check if the current epoch’s validation loss (val_loss) dips below best_loss, it means we’re making progress. We update best_loss to this new low, and also save the current model weights as best_weights. This way, we always have a snapshot of the model at its peak performance. We then reset the epochs_no_improve count to zero since we just saw an improvement.
If there’s no drop in val_loss, we increase epochs_no_improve by one, indicating another epoch has passed without betterment.
If our epochs_no_improve count hits the patience limit we’ve set, it’s our cue that the model isn’t likely to get any better, so we trigger early stopping. We let everyone know with a message and revert the model’s weights back to best_weights, the gold standard we’ve been keeping track of. Then, we exit the training loop.
This approach gives us a balanced way to halt training — not too soon, so we give the model a fair chance to learn, but not too late, where we’re just wasting time or risking overfitting.
3.3: Initialization Methods
When setting up a neural network, how you kick off the weights can change the game in terms of how well and how quickly the network learns. Let’s go over a few different ways to initialize weights — random, zeros, Glorot (Xavier), and He initialization — and what makes each method unique.
Random Initialization
Going the random route means setting up the initial weights by pulling numbers from a distribution, usually either uniform or normal. This randomness helps ensure that no two neurons start the same, allowing them to learn different things as the network trains. The trick is picking a variance that’s just right — too much, and you risk blowing up the gradients; too little, and they might disappear.
weights = np.random.randn(layers[i], layers[i + 1])
This line of code plucks weights from a standard normal distribution, setting the stage for each neuron to potentially go down its path of learning.
Pros: It’s a straightforward approach that helps prevent neurons from mimicking each other.
Cons: Getting the variance wrong can cause the learning process to be unstable.
Zeros Initialization
Setting all weights to zero is about as simple as it gets. However, this method has a major downside: it makes every neuron in a layer effectively the same. This sameness can stunt the network’s learning, as every neuron on the same layer will update identically during training.
weights = np.zeros((layers[i], layers[i + 1]))
Here, we end up with a weight matrix full of zeros. It’s neat and orderly, but it also means every path through the network initially carries the same weight, which isn’t great for learning diversity.
Pros: Very easy to implement.
Cons: It handcuffs the learning process, usually resulting in subpar network performance.
Glorot Initialization
Designed specifically for networks with sigmoid activation functions, Glorot initialization sets the weights based on the number of input and output units in the network. It aims to maintain the variance of activations and back-propagated gradients through the layers, preventing the vanishing or exploding gradient problem.
The weights in the Glorot initialization can be drawn either by a uniform distribution or a normal distribution. For uniform distribution, weights are initialized using the range [−a, a], where a is:
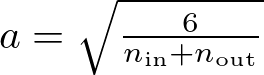
def glorot_uniform(self, fan_in, fan_out):
limit = np.sqrt(6 / (fan_in + fan_out))
return np.random.uniform(-limit, limit, (fan_in, fan_out))
weights = glorot_uniform(layers[i - 1], layers[i])
This formula ensures the weights start spread evenly, are ready to catch, and maintain a good gradient flow.
For a normal distribution:
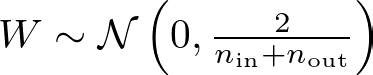
def glorot_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / (fan_in + fan_out))
return np.random.normal(0., stddev, size=(fan_in, fan_out))
weights = self.glorot_normal(layers[i - 1], layers[i])
This adjustment keeps the weights spread just right for networks leaning on sigmoid activations.
Pros: Maintains gradient variance in a reasonable range, improving the stability of deep networks.
Cons: May not be optimal for layers with ReLU (or variants) activations due to different signal propagation characteristics.
He Initialization
He initialization, tailored for layers with ReLU activation functions, adjusts the variance of the weights considering the non-linear characteristics of ReLU. This strategy helps maintain a healthy gradient flow through the network, especially important in deep networks where ReLU is commonly used.
Like the Glorot initialization, the weights can be drawn either from a uniform or normal distribution.
For the uniform distribution, the weights are initialized using the range [−a, a], where a is calculated as:

Thus, the weights W are drawn from a uniform distribution as:
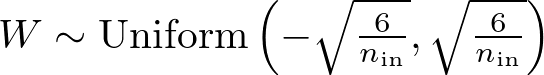
def he_uniform(self, fan_in, fan_out):
limit = np.sqrt(2 / fan_in)
return np.random.uniform(-limit, limit, (fan_in, fan_out))
weights = self.he_uniform(layers[i - 1], layers[i])
When using a normal distribution, the weights are initialized according to the formula:
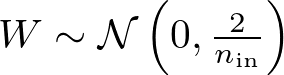
where W represents the weights, N denotes the normal distribution, 0 is the mean of the distribution, and 2/n is the variance. n-in is the number of input units to the layer.
def he_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / fan_in)
return np.random.normal(0., stddev, size=(fan_in, fan_out))
weights = self.he_normal(layers[i - 1], layers[i])
In both cases, the initialization strategy aims to account for the properties of the ReLU activation function, which does not activate all neurons in the layer due to its non-negative output for positive input. This adjustment in the variance of the initial weights helps prevent the diminishing or exploding of gradients that can occur in deep networks, promoting a more stable and efficient training process.
Pros: Facilitates deep learning models’ training by preserving gradient magnitudes in networks with ReLU activations.
Cons: It’s specifically optimized for ReLU and might not be as effective as other activation functions.
Let’s take a look now at how the NeuralNetwork class looks like after introducing the initializations:
class NeuralNetwork:
def __init__(self,
layers,
init_method='glorot_uniform', # 'zeros', 'random', 'glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal'
loss_func='mse',
):
...
self.init_method = init_method
# Initialize layers
for i in range(len(layers) - 1):
if self.init_method == 'zeros':
weights = np.zeros((layers[i], layers[i + 1]))
elif self.init_method == 'random':
weights = np.random.randn(layers[i], layers[i + 1])
elif self.init_method == 'glorot_uniform':
weights = self.glorot_uniform(layers[i], layers[i + 1])
elif self.init_method == 'glorot_normal':
weights = self.glorot_normal(layers[i], layers[i + 1])
elif self.init_method == 'he_uniform':
weights = self.he_uniform(layers[i], layers[i + 1])
elif self.init_method == 'he_normal':
weights = self.he_normal(layers[i], layers[i + 1])
else:
raise ValueError(f'Unknown initialization method {self.init_method}')
self.layers.append({
'weights': weights,
'biases': np.zeros((1, layers[i + 1]))
})
...
...
def glorot_uniform(self, fan_in, fan_out):
limit = np.sqrt(6 / (fan_in + fan_out))
return np.random.uniform(-limit, limit, (fan_in, fan_out))
def he_uniform(self, fan_in, fan_out):
limit = np.sqrt(2 / fan_in)
return np.random.uniform(-limit, limit, (fan_in, fan_out))
def glorot_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / (fan_in + fan_out))
return np.random.normal(0., stddev, size=(fan_in, fan_out))
def he_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / fan_in)
return np.random.normal(0., stddev, size=(fan_in, fan_out))
...
Choosing the right weight initialization strategy is crucial for effective neural network training. While random and zeros initialization offers fundamental approaches, they might not always lead to optimal learning dynamics. In contrast, Glorot/Xavier and He initialization provides more sophisticated solutions that address the specific needs of deep learning models, considering the network architecture and activation functions used. These strategies help in balancing the trade-offs between too rapid and too slow learning, steering the training process towards more reliable convergence.
3.4: Dropout
Dropout is a regularization technique designed to prevent overfitting in neural networks by temporarily and randomly removing units (neurons) along with their connections from the network during the training phase. This method was introduced by Srivastava et al. in their 2014 paper as a simple yet effective way to train robust neural networks.
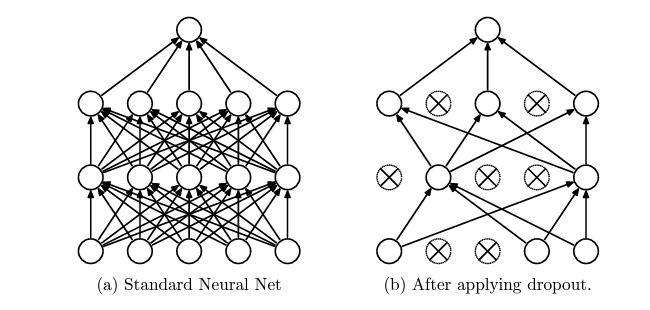
overfitting”, JMLR 2014
During each training iteration, each neuron (including input units but typically not the output units) has a probability p of being temporarily “dropped out,” meaning it is entirely ignored during this forward and backward pass. This probability p, often referred to as the “dropout rate,” is a hyperparameter that can be adjusted to optimize performance. For instance, a dropout rate of 0.5 means each neuron has a 50% chance of being omitted from the computation on each training pass.
The effect of this process is that the network becomes less sensitive to the specific weights of any one neuron. This is because it cannot rely on any individual neuron’s output when making predictions, thus encouraging the network to spread out importance among its neurons. It effectively trains a pseudo-ensemble of neural networks with shared weights, where each training iteration involves a different “thinned” version of the network. At test time, dropout is not applied, and instead, the weights are typically scaled by the dropout rate p to balance the fact that more units are active than during training.
Choosing the Right Dropout Rate
The dropout rate is a hyperparameter that requires tuning for each neural network architecture and dataset. Commonly, a rate of 0.5 is used for hidden units as a starting point, as suggested in the original dropout paper.
A high dropout rate (close to 1) means more neurons are dropped during training. This can lead to underfitting, as the network may not be able to learn the data sufficiently, struggling to model the complexity of the training data.
Conversely, a low dropout rate (close to 0) results in fewer neurons being dropped, which might reduce the regularization effect of dropout and could lead to overfitting, where the model performs well on the training data but poorly on unseen data.
Code Implementation
Let’s see how this looks in our code:
class NeuralNetwork:
def __init__(self,
layers,
init_method='glorot_uniform', # 'zeros', 'random', 'glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal'
loss_func='mse',
dropout_rate=0.5
):
...
self.dropout_rate = dropout_rate
...
...
def forward(self, X, is_training=True):
self.a = [X]
for i, layer in enumerate(self.layers):
z = np.dot(self.a[-1], layer['weights']) + layer['biases']
a = self.sigmoid(z)
if is_training and i < len(self.layers) - 1: # apply dropout to all layers except the output layer
dropout_mask = np.random.rand(*a.shape) > self.dropout_rate
a *= dropout_mask
self.a.append(a)
return self.a[-1]
...
Our neural network class has gotten an upgrade with new initialization parameters and a forward propagation method that now includes dropout regularization.
dropout_rate : This is a setting that decides how likely it is for neurons to be temporarily removed from the network during training, helping to avoid overfitting. By setting it to 0.5, we’re saying there’s a 50% chance that any given neuron will be “dropped” in a training round. This randomness helps ensure the network doesn’t become too dependent on any single neuron, promoting a more robust learning process.
The is_training boolean flag tells the network whether it’s currently being trained. This is important because dropout is something you’d only want to happen during training, not when you’re evaluating the network’s performance on new data.
As data (denoted as X) makes its way through the network, the network calculates a weighted sum (z) of the incoming data and the layer’s biases. It then runs this sum through the sigmoid activation function to get the activations (a), which are the signals that will be passed on to the next layer.
But before we proceed to the next layer during training, we might apply dropout:
- If is_training is true and we’re not dealing with the output layer, we roll the dice for each neuron to see if it gets dropped. We do this by creating a dropout_mask—an array shaped just like a. Each element in this mask is the outcome of checking if a random number exceeds the dropout_rate.
- We then use this mask to zero out some of the activations in a, effectively simulating the temporary removal of neurons from the network.
After we’ve applied dropout (when applicable), we add the resulting activations to self.a, our list that keeps track of the activations across all layers. This way, we’re not just blindly moving signals from one layer to the next; we’re also applying a technique that encourages the network to learn more robustly, making it less likely to rely too heavily on any specific pathway of neurons.
3.5: Gradient Clipping
Gradient clipping is a crucial technique in training deep neural networks, especially in dealing with the problem of exploding gradients. Exploding gradients occur when the derivatives or gradients of the loss function for the network’s parameters grow exponentially through the layers, leading to very large updates to the weights during training. This can cause the learning process to become unstable, often manifesting as NaN values in the weights or loss due to numerical overflow, which in turn prevents the model from converging to a solution.
Gradient clipping can be implemented in two primary ways: by value and by norm, each with its strategy for mitigating the issue of exploding gradients.
Clipping by Value
This approach involves setting a predefined threshold value, and directly clipping each gradient component to be within a specified range if it exceeds this threshold. For example, if the threshold is set to 1, every gradient component greater than 1 is set to 1, and every component less than -1 is set to -1. This ensures that all gradients remain within the range [-1, 1], effectively preventing any gradient from becoming too large.
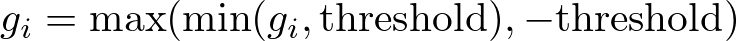
where gi represents each component of the gradient vector.
Clipping by Norm
Instead of clipping each gradient component individually, this method scales the whole gradient if its norm exceeds a certain threshold. This preserves the direction of the gradient while ensuring its magnitude does not exceed the specified limit. This is particularly useful in maintaining the relative direction of the updates across all parameters, which can be more beneficial for the learning process than clipping by value.
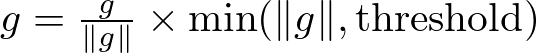
where g is the gradient vector and ∥g∥ is its norm.
Application in Training
class NeuralNetwork:
def __init__(self,
layers,
init_method='glorot_uniform', # 'zeros', 'random', 'glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal'
loss_func='mse',
dropout_rate=0.5,
clip_type='value',
grad_clip=5.0
):
...
self.clip_type = clip_type
self.grad_clip = grad_clip
...
...
def backward(self, X, y, learning_rate):
m = X.shape[0]
self.dz = [self.a[-1] - y]
self.gradient_norms = [] # List to store the gradient norms
for i in reversed(range(len(self.layers) - 1)):
self.dz.append(np.dot(self.dz[-1], self.layers[i + 1]['weights'].T) * self.sigmoid_derivative(self.a[i + 1]))
self.gradient_norms.append(np.linalg.norm(self.layers[i + 1]['weights'])) # Compute and store the gradient norm
self.dz = self.dz[::-1]
self.gradient_norms = self.gradient_norms[::-1] # Reverse the list to match the order of the layers
for i in range(len(self.layers)):
grads_w = np.dot(self.a[i].T, self.dz[i]) / m
grads_b = np.sum(self.dz[i], axis=0, keepdims=True) / m
# gradient clipping
if self.clip_type == 'value':
grads_w = np.clip(grads_w, -self.grad_clip, self.grad_clip)
grads_b = np.clip(grads_b, -self.grad_clip, self.grad_clip)
elif self.clip_type == 'norm':
grads_w = self.clip_by_norm(grads_w, self.grad_clip)
grads_b = self.clip_by_norm(grads_b, self.grad_clip)
self.layers[i]['weights'] -= learning_rate * grads_w
self.layers[i]['biases'] -= learning_rate * grads_b
def clip_by_norm(self, grads, clip_norm):
l2_norm = np.linalg.norm(grads)
if l2_norm > clip_norm:
grads = grads / l2_norm * clip_norm
return grads
...
During the initialization, we now have the type of gradient clipping to use (clip_type), and the gradient clipping threshold (grad_clip).
clip_type can be either ‘value’ for clipping gradients by value or ‘norm’ for clipping gradients by their L2 norm. grad_clip specifies the threshold or limit for the clipping.
Then, during the backward pass, the function computes the gradients for each layer in the network by performing backpropagation. It calculates the derivatives of the loss for the weights (grads_w) and biases (grads_b) for each layer.
If clip_type is ‘value’, gradients are clipped to be within the range [-grad_clip, grad_clip] using np.clip. This ensures no gradient component exceeds these bounds.
If clip_type is ‘norm’, the clip_by_norm method is called to scale down the gradients if their norm exceeds grad_clip, preserving their direction but limiting their magnitude.
After clipping, the gradients are used to update the weights and biases of each layer, scaled by the learning rate.
Lastly, we create a clip_by_norm method, which scales the gradients if their L2 norm exceeds the specified clip_norm. It calculates the L2 norm of the gradients and, if it’s greater than clip_norm, scales the gradients down to the clip_norm while preserving their direction. This is achieved by dividing the gradients by their L2 norm and multiplying by clip_norm.
Benefits of Gradient Clipping
By preventing excessively large updates to the model’s weights, gradient clipping contributes to a more stable and reliable training process. It allows the optimizer to make consistent progress in minimizing the loss function, even in cases where the calculation of gradients might otherwise lead to instability due to the scale of updates. This makes it a valuable tool in the training of deep neural networks, particularly in tasks such as training recurrent neural networks (RNNs), where the problem of exploding gradients is more prevalent.
Gradient clipping represents a straightforward yet powerful technique to enhance the stability and performance of neural network training. By ensuring that gradients do not become excessively large, it helps avoid the pitfalls of training instability, such as overfitting, underfitting, and slow convergence, making it easier for neural networks to learn effectively and efficiently.
4: Determining the Optimal Number of Layers
One of the pivotal decisions in designing a neural network is determining the right number of layers. This aspect significantly influences the network’s ability to learn from data and generalize to new, unseen data. The depth of a neural network — how many layers it has — can either empower its learning capacity or lead to challenges like overfitting or underlearning.
4.1: Layer Depth and Model Performance
Adding more layers to a neural network enhances its learning capacity, enabling it to capture more complex patterns and relationships in the data. This is because additional layers can create more abstract representations of the input data, moving from simple features to more complex combinations.
While deeper networks can model complex patterns, there’s a tipping point where additional depth might lead to overfitting. Overfitting occurs when the model learns the training data too well, including its noise, making it perform poorly on new data.
The ultimate goal is to have a model that not only learns well from the training data but can also generalize this learning to perform accurately on data it hasn’t seen before. Finding the right balance in layer depth is crucial for this; too few layers might underfit, while too many can overfit.
4.2: Strategies for Testing and Selecting the Appropriate Depth
Incremental Approach
Begin with a simpler model, then gradually add layers until you notice a significant improvement in validation performance. This approach helps in understanding the contribution of each layer to the overall performance.
Use the model’s performance on a validation set (a subset of the training data not used during training) as a benchmark for deciding whether adding more layers improves the model’s ability to generalize.
Regularization Techniques
Employ regularization methods like dropout or L2 regularization as you add more layers. These techniques can mitigate the risk of overfitting, allowing for a fair assessment of the added layers’ value to the model’s learning capacity.
Observing Training Dynamics
Monitor the training and validation loss as you add more layers. A divergence between these two metrics — where training loss decreases but validation loss does not — might indicate overfitting, suggesting that the current depth might be excessive.
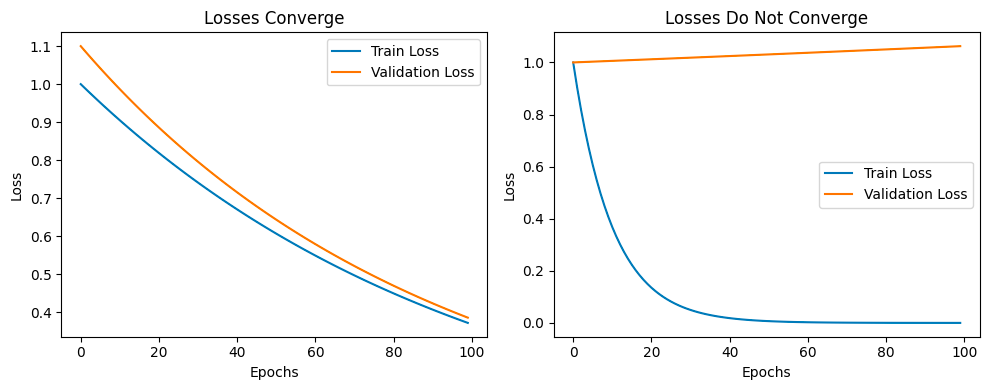
The two graphs represent two different scenarios that can occur during the training of a machine learning model.
In the first graph, both the training loss and the validation loss decrease and converge to a similar value. This is an ideal scenario, indicating that the model is learning and generalizing well. The model’s performance is improving on both the training data and unseen validation data. This suggests that the model is neither underfitting nor overfitting the data.
In the second graph, the training loss decreases, but the validation loss increases. This is a classic sign of overfitting. The model is learning the training data too well, including its noise and outliers, and is failing to generalize to unseen data. As a result, its performance on the validation data gets worse over time. This indicates that the model’s complexity may need to be reduced, or other techniques to prevent overfitting may need to be applied, such as regularization or dropout.
Automated Architecture Search
Utilize neural architecture search (NAS) tools or hyperparameter optimization frameworks like Optuna to explore different architectures systematically. These tools can automate the search for an optimal number of layers by evaluating numerous configurations and selecting the one that performs best on validation metrics.
Determining the optimal number of layers in a neural network is a nuanced process that balances the model’s complexity with its ability to learn and generalize. By adopting a methodical approach to layer addition, employing cross-validation, and integrating regularization techniques, you can identify a network depth that suits your specific problem, optimizing your model’s performance on unseen data.
5: Automated Fine-Tuning with Optuna
Fine-tuning neural networks to achieve optimal performance involves a delicate balance of various hyperparameters, which can often feel like finding a needle in a haystack due to the vast search space. This is where automated hyperparameter optimization tools like Optuna come into play.
5.1: Introduction to Optuna
Optuna is an open-source optimization framework designed to automate the selection of optimal hyperparameters. It simplifies the complex task of identifying the best combination of parameters that lead to the most efficient neural network model. Here, Optuna employs sophisticated algorithms to explore the hyperparameter space more effectively, reducing both the computational resources required and the time to convergence.
5.2: Integrating Optuna for Neural Network Optimization
Optuna uses a variety of strategies, such as Bayesian optimization, tree-structured Parzen estimators, and even evolutionary algorithms, to intelligently navigate the hyperparameter space. This approach allows Optuna to quickly hone in on the most promising hyperparameters, significantly speeding up the optimization process.
Integrating Optuna into the neural network training workflow involves defining an objective function that Optuna will aim to minimize or maximize. This function typically includes the model training and validation process, with the goal being to minimize the validation loss or maximize validation accuracy.
- Defining the Search Space: You specify the range of values for each hyperparameter (e.g., number of layers, learning rate, dropout rate) that Optuna will explore.
- Trial and Evaluation: Optuna conducts trials, each time selecting a new set of hyperparameters to train the model. It evaluates the model’s performance on a validation set and uses this information to guide the search.
5.3: Practical Implementation
import optuna
def objective(trial):
# Define hyperparameters
n_layers = trial.suggest_int('n_layers', 1, 10)
hidden_sizes = [trial.suggest_int(f'hidden_size_{i}', 32, 128) for i in range(n_layers)]
dropout_rate = trial.suggest_uniform('dropout_rate', 0.0, 0.5) # single dropout rate for all layers
learning_rate = trial.suggest_loguniform('learning_rate', 1e-3, 1e-1)
init_method = trial.suggest_categorical('init_method', ['glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal', 'random'])
clip_type = trial.suggest_categorical('clip_type', ['value', 'norm'])
clip_value = trial.suggest_uniform('clip_value', 0.0, 1.0)
epochs = 10000
layers = [input_size] + hidden_sizes + [output_size]
# Create and train the neural network
nn = NeuralNetwork(layers=layers, loss_func=loss_func, dropout_rate=dropout_rate, init_method=init_method, clip_type=clip_type, grad_clip=clip_value)
trainer = Trainer(nn, loss_func)
trainer.train(X_train, y_train, X_test, y_test, epochs, learning_rate, early_stopping=False)
# Evaluate the performance of the neural network
predictions = np.argmax(nn.forward(X_test), axis=1)
accuracy = np.mean(predictions == y_test_labels)
return accuracy
# Create a study object and optimize the objective function
study = optuna.create_study(study_name='nn_study', direction='maximize')
study.optimize(objective, n_trials=100)
# Print the best hyperparameters
print(f"Best trial: {study.best_trial.params}")
print(f"Best value: {study.best_trial.value:.3f}")
The core of the Optuna optimization process is the objective function, which defines the trial’s objective and is called by Optuna for each trial.
Heren_layers is the number of hidden layers in the neural network, suggested between 1 and 10. Varying the number of layers allows exploration of shallow versus deep network architectures.
hidden_sizes stores the size (number of neurons) for each layer, suggesting a number between 32 and 128, allowing the model to explore different capacities.
dropout_rate is uniformly suggested between 0.0 (no dropout) and 0.5, enabling regularization flexibility across trials.
learning_rate is suggested on a log scale between 1e-3 and 1e-1, ensuring a wide search space that spans orders of magnitude, which is common for learning rate optimization due to its sensitivity.
init_method for the neural network weights, chosen from a set of common strategies. This choice affects the starting point of training and thus the convergence behavior.
clip_type and clip_value define the gradient clipping strategy and value, helping to prevent exploding gradients by either clipping by value or norm.
Then, theNeuralNetwork instance is created and trained using the defined hyperparameters. Note that early stopping is disabled to allow each trial to run for a fixed number of epochs, ensuring consistent comparison. The performance is evaluated based on the accuracy of the model’s predictions on the test set.
Once the objective function and the NeuralNetwork instance are defined, we can move on to the Optuna study, whose object is created to maximize the objective function (‘maximize’), which in this context is the accuracy of the neural network.
The study calls the objective function multiple times (n_trials=100), each time with a different set of hyperparameters suggested by Optuna’s internal optimization algorithms. Optuna intelligently adjusts its suggestions based on the history of trials to explore the hyperparameter space efficiently.
The process yields the best set of hyperparameters found across all trials (study.best_trial.params) and the highest accuracy achieved (study.best_trial.value). This output provides insights into the optimal configuration of the neural network for the task at hand.
5.4: Benefits and Outcomes
By integrating Optuna, developers can not only automate the hyperparameter tuning process but also gain deeper insights into how different parameters affect their models. This leads to more robust and accurate neural networks, optimized in a fraction of the time it would take through manual experimentation.
Optuna’s systematic approach to fine-tuning brings a new level of precision and efficiency to neural network development, empowering developers to achieve higher performance standards and push the boundaries of what their models can accomplish.
5.5: Limitations
While Optuna offers a powerful and flexible approach to hyperparameter optimization, several limitations and considerations should be acknowledged when integrating it into machine learning workflows:
Computational Resources
Each trial involves training a neural network from scratch, which can be computationally expensive, especially with deep networks or large datasets. Running hundreds or thousands of trials to explore the hyperparameter space thoroughly can require significant computational resources and time.
Hyperparameter Search Space
The effectiveness of Optuna’s search depends heavily on how the search space is defined. If the range of values for hyperparameters is too broad or not properly aligned with the problem, Optuna might spend time exploring suboptimal regions. Conversely, too narrow a search space might miss the optimal configurations.
As the number of hyperparameters increases, the search space grows exponentially, a phenomenon known as the “curse of dimensionality.” This can make it challenging for Optuna to efficiently navigate the space and find the best hyperparameters within a reasonable number of trials.
Evaluation Metrics
The choice of the objective function and evaluation metrics can significantly impact the outcomes of optimization. Metrics that do not adequately capture the model’s performance or objectives of the task might lead to suboptimal hyperparameter configurations.
The performance evaluation of a model can vary due to factors like random initialization, data shuffling, or inherent noise in the dataset. This variability can introduce noise into the optimization process, potentially affecting the reliability of the results.
Algorithmic Limitations
Optuna uses sophisticated algorithms to navigate the search space, but the efficiency and effectiveness of these algorithms can vary depending on the problem. In some cases, certain algorithms might converge to local optima or require adjustment in their settings to better suit the specific characteristics of the hyperparameter space.
6: Conclusion
As we wrap up our deep dive into fine-tuning neural networks, it’s a good moment to look back on the path we’ve traveled. We started with the basics of how neural networks function and steadily progressed to more sophisticated techniques that boost their performance and efficiency.
6.1: What’s Next
While we’ve covered a lot of ground in optimizing neural networks, it’s clear we’ve only scratched the surface. The landscape of neural network optimization is vast and continuously evolving, brimming with techniques and strategies we haven’t yet explored. In our upcoming articles, we’re set to dive deeper, exploring more complex neural network architectures and the advanced techniques that can unlock even higher levels of performance and efficiency.
There’s a whole array of optimization techniques and concepts we plan to delve into, including:
- Batch Normalization: A method that helps speed up training and improves stability by normalizing the input layer by adjusting and scaling the activations.
- Optimization algorithms: including SGD and Adam, provide us with tools to navigate the complex landscape of the loss function more effectively, ensuring more efficient training cycles and better model performance.
- Transfer Learning and Fine-Tuning: Leveraging pre-trained models and adapting them to new tasks can drastically reduce training time and improve model accuracy on tasks with limited data.
- Neural Architecture Search (NAS): Using automation to discover the best architecture for a neural network, potentially uncovering efficient models that might not be intuitive to human designers.
These topics represent just a taste of what’s out there, each offering unique advantages and challenges. As we move forward, we aim to unpack these techniques, providing insights into how they work, when to use them, and the impact they can have on your neural network projects.
Further Resources
- “Deep Learning” by Ian Goodfellow, Yoshua Bengio, and Aaron Courville: This comprehensive text offers an in-depth overview of deep learning techniques and principles, including advanced neural network architectures and optimization methods.
- “Neural Networks and Deep Learning: A Textbook” by Charu C. Aggarwal: This book provides a detailed exploration of neural networks, with a focus on deep learning and its applications. It’s an excellent resource for understanding complex concepts in neural network design and optimization.
You made it to the end. Congrats! I hope you enjoyed this article, if so consider leaving a like and following me, as I will regularly post similar articles. My goal is to recreate all the most popular algorithms from scratch and make machine learning accessible to everyone.
The Math Behind Fine-Tuning Deep Neural Networks was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The Math Behind Fine-Tuning Deep Neural Networks
Go Here to Read this Fast! The Math Behind Fine-Tuning Deep Neural Networks