Evaluating machine learning models beyond training data
Introduction
In recent years, data-driven approaches such as machine learning (ML) and deep learning (DL) have been applied to a wide range of tasks including machine translation and personal customized recommendations. These technologies reveal some patterns within the given training dataset by analyzing numerous data. However, if the given dataset has some biases and does not include the data that you want to know or predict, it might be difficult to get the correct answer from the trained model.
Let’s think about the case of ChatGPT. The latest version of ChatGPT at this time is ChatGPT 4o, and this model is trained on data until June 2023 (at the period of this article). Therefore, if you ask about something that happened in 2024 not included in the training data, you will not get an accurate answer. This is well-known as “hallucination,” and OpenAI added the preprocessing procedure to return a fixed answer as “unanswerable” for such kinds of questions. ChatGPT’s training data is also basically based on documents written in English, so it is not good at local domain knowledge outside of English-native countries such as Japan and France. Therefore, many companies and research groups put a lot of effort into customizing their LLM by including the region or domain-specific knowledge using RAG (Retrieval-Augmented Generation) or fine-tuning.
Hence, identifying what training data is used is important for understanding the applicability and limitations of AI models. On the other hand, one of the biggest challenges in data-driven approaches is that these technologies often need to perform beyond the range of the training dataset. These demands are typically seen in new product development in material science, predicting the effects of new pharmaceutical compounds, and predicting consumer behavior when launching products in the markets. These scenarios require the correct predictions in the sparse area and outside of the training data, which refer to interpolation and extrapolation.

Interpolation involves making predictions within the known data range. If the training data is densely and uniformly distributed, accurate predictions can be obtained within that range. However, in practice, preparing such data is uncommon. On the other hand, extrapolation refers to making predictions outside the known data points’ range. Although predictions in such areas are highly desired, data-driven approaches typically struggle the most. Consequently, it is significantly important to understand the performance of both interpolation and extrapolation for each algorithm.

This article examines various machine learning algorithms for their interpolation and extrapolation capabilities. We prepare an artificial training dataset and evaluate these capabilities by visualizing each model’s prediction results. The target of machine learning algorithms are as follows:
- Symbolic Regressor
- SVR (Support Vector Regression)
- Gaussian Process Regressor (GPR)
- Decision Tree Regressor
- Random Forest Regressor
- XGBoost
- LightGBM
In addition, we also evaluate ensemble models such as Voting Regressor and Stacking Regressor.
Codes
Full of codes are available from below:
blog_TDS/02_compare_regression at main · rkiuchir/blog_TDS
Data Generation and Preprocessing
Firstly, we generate the artificial data using a simple nonlinear function that is slightly modified from the symbolic regressor’s tutorial in gplearn by adding the exponential term. This function consists of linear, quadratic, and exponential terms, defined as follows:
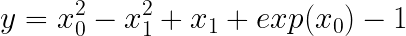
where x₀ and x₁ take a range of -1 to 1. The plane of ground truth is as shown below:
Since we examine the performance of each ML model in terms of interpolation and extrapolation, different datasets will be needed for each case.
For interpolation, we evaluate the model performance within the same range as with the training dataset. Therefore, each model will be trained with discretized data points within the range of -1 to 1 and evaluated the predicted surface within the same range.
On the other hand, for extrapolation, the capability of the model within the range outside of the training dataset will be required. We will train the model using the discretized data points within the range of -0.5 to 1 for both x₀ and x₁ and assess the predicted surface within the range of -1 to 1. Consequently, the difference between the ground truth and predicted surface in the range of -1 to -0.5 for both x₀ and x₁ reveals the model capability in terms of extrapolation.
In this article, the impact of the number of points for the training dataset will be evaluated by examining two cases: 20 and 100 points.
For example, 100 data points are generated as follows:
import numpy as np
def target_function(x0, x1):
return x0**2 - x1**2 + x1 + np.exp(x0) - 1
# Generate training data for interpolation
X_train = rng.uniform(-1, 1, 200).reshape(100, 2)
y_train = target_function(X_train[:, 0], X_train[:, 1])
# Generate training data for extrapolation
X_train = rng.uniform(-0.5, 1, 200).reshape(100, 2)
y_train = target_function(X_train[:, 0], X_train[:, 1])
Introduction to Machine Learning Algorithms
In this article, we evaluate the performance of interpolation and extrapolation for the major 7 machine learning algorithms. In addition, the 6 ensemble models using 7 algorithms are also considered. Each algorithm has different structures and aspects, that introduce pros and cons for predicting performance. Here we summarize the characteristics of each algorithm as follows:
- Symbolic Regression
- A trained model is expressed as the mathematical expressions fitted based on the genetic algorithms
- Model is defined as the function, contributing high interpretability
- Appropriate for the task that target variable can be expressed as a function of features
- Good at interpolation but may have some potential in extrapolation
Find Hidden Laws Within Your Data with Symbolic Regression
2. Support Vector Regression (SVR)
- Based on a Support Vector Machine (SVM) that can efficiently handle the nonlinear relationship in the high dimensional spaces using the kernel method
- Using different types of kernels such as linear, RBF, polynomial, and sigmoid kernels, a model can express complex data patterns
- Good at interpolation but less stable in extrapolation
The Complete Guide to Support Vector Machine (SVM)
3. Gaussian Process Regression (GPR)
- Based on the Bayesian method, the prediction is expressed as the probability which includes the predicted value and its uncertainty
- Thanks to the uncertainty estimation, GPR used for Bayesian Optimization
- Using different types of kernels such as linear, RBF, polynomial, and sigmoid kernels, a model can express complex data patterns
- Good at interpolation, and some potential for extrapolation selecting appropriate kernel selection
Quick Start to Gaussian Process Regression
4. Decision Tree
- Simple tree-shape algorithm which successively splits the data
- Easy to understand and interpret but tends to overfit
- Step-like estimation for interpolation and not good at extrapolation
Decision Tree in Machine Learning
5. Random Forest
- An ensemble-based algorithm which is called “Bagging” consisting of multiple decision trees
- By combining multiple diverse trees, this algorithm can reduce overfitting risk and have a high interpolation performance
- More stable predictions than single decision trees but not good at extrapolation
6. XGBoost
- An ensemble-based algorithm which is called “Boosting” combines multiple decision trees by sequentially reducing errors
- Commonly used for competition such as Kaggle because of the good prediction performance
- More stable predictions than single decision trees but not good at extrapolation
XGBoost: A Deep Dive into Boosting
7. LightGBM
- Similar to XGBoost, but with faster training speed and memory efficiency, which is more suitable for the larger datasets
- More stable predictions than single decision trees but not good at extrapolation
What is LightGBM, How to implement it? How to fine tune the parameters?
8. Voting Regressor
- An ensemble learning method combining predictions from multiple models
- Mixing different model characteristics, which contribute to more robust predictions than a single model
- Evaluated in three combinations in this article:
– Support Vector Regressor + Random Forest
– Gaussian Process Regressor + Random Forest
– Random Forest + XGBoost
9. Stacking Regressor
- An ensemble learning method that uses predictions from multiple models as input for a final prediction model, “meta-model”
- Meta model covers individual model weaknesses and combines each model’s strengths
- Evaluated in three combinations in this article:
– Base model: Support Vector Regressor + Random Forest; Meta-model: Random Forest
– Base model: Gaussian Process Regressor + Random Forest; Meta-model: Random Forest
– Base model: Random Forest + XGBoost; Meta-model: Random Forest
Using these algorithms, we will evaluate both interpolation and extrapolation performance with the dataset we generated earlier. In the following sections, the training methods and evaluation approaches for each model will be explained.
Model Training and Evaluation
Preprocessing
Basically, except for tree-based approaches such as Random Forest, XGBoost, and LightGBM, most machine learning algorithms require feature scaling. However, since we only use two features such as x₀ and x₁ which take the same range, -1 to 1 (interpolation) or -0.5 to 1 (extrapolation) in this practice, we will skip the feature scaling.
Model Training
For simplicity, parameter tuning is not done for all algorithms except LightGBM of which default parameters are suitable for the larger dataset.
As introduced in the earlier section, we will use different datasets for the evaluation of interpolation and extrapolation during model training.
Evaluation and Visualization
After model training, we will predict using very finely discretized data. Based on these predicted values, the prediction surface will be drawn using the Plotly surface function.
These procedures are done by the following code:
class ModelFitterAndVisualizer:
def __init__(self, X_train, y_train, y_truth, scaling=False, random_state=41):
"""
Initialize the ModelFitterAndVisualizer class with training and testing data.
Parameters:
X_train (pd.DataFrame): Training data features
y_train (pd.Series): Training data target
y_truth (pd.Series): Ground truth for predictions
scaling (bool): Flag to indicate if scaling should be applied
random_state (int): Seed for random number generation
"""
self.X_train = X_train
self.y_train = y_train
self.y_truth = y_truth
self.initialize_models(random_state)
self.scaling = scaling
# Initialize models
# -----------------------------------------------------------------
def initialize_models(self, random_state):
"""
Initialize the models to be used for fitting and prediction.
Parameters:
random_state (int): Seed for random number generation
"""
# Define kernel for GPR
kernel = 1.0 * RBF(length_scale=1.0) + WhiteKernel(noise_level=1.0)
# Define Ensemble Models Estimator
# Decision Tree + Kernel Method
estimators_rf_svr = [
('rf', RandomForestRegressor(n_estimators=30, random_state=random_state)),
('svr', SVR(kernel='rbf')),
]
estimators_rf_gpr = [
('rf', RandomForestRegressor(n_estimators=30, random_state=random_state)),
('gpr', GaussianProcessRegressor(kernel=kernel, normalize_y=True, random_state=random_state))
]
# Decision Trees
estimators_rf_xgb = [
('rf', RandomForestRegressor(n_estimators=30, random_state=random_state)),
('xgb', xgb.XGBRegressor(random_state=random_state)),
]
self.models = [
SymbolicRegressor(random_state=random_state),
SVR(kernel='rbf'),
GaussianProcessRegressor(kernel=kernel, normalize_y=True, random_state=random_state),
DecisionTreeRegressor(random_state=random_state),
RandomForestRegressor(random_state=random_state),
xgb.XGBRegressor(random_state=random_state),
lgbm.LGBMRegressor(n_estimators=50, num_leaves=10, min_child_samples=3, random_state=random_state),
VotingRegressor(estimators=estimators_rf_svr),
StackingRegressor(estimators=estimators_rf_svr,
final_estimator=RandomForestRegressor(random_state=random_state)),
VotingRegressor(estimators=estimators_rf_gpr),
StackingRegressor(estimators=estimators_rf_gpr,
final_estimator=RandomForestRegressor(random_state=random_state)),
VotingRegressor(estimators=estimators_rf_xgb),
StackingRegressor(estimators=estimators_rf_xgb,
final_estimator=RandomForestRegressor(random_state=random_state)),
]
# Define graph titles
self.titles = [
"Ground Truth", "Training Points",
"SymbolicRegressor", "SVR", "GPR",
"DecisionTree", "RForest",
"XGBoost", "LGBM",
"Vote_rf_svr", "Stack_rf_svr__rf",
"Vote_rf_gpr", "Stack_rf_gpr__rf",
"Vote_rf_xgb", "Stack_rf_xgb__rf",
]
def fit_models(self):
"""
Fit the models to the training data.
Returns:
self: Instance of the class with fitted models
"""
if self.scaling:
scaler_X = MinMaxScaler()
self.X_train_scaled = scaler_X.fit_transform(self.X_train)
else:
self.X_train_scaled = self.X_train.copy()
for model in self.models:
model.fit(self.X_train_scaled, self.y_train)
return self
def visualize_surface(self, x0, x1, width=400, height=500,
num_panel_columns=5,
vertical_spacing=0.06, horizontal_spacing=0,
output=None, display=False, return_fig=False):
"""
Visualize the prediction surface for each model.
Parameters:
x0 (np.ndarray): Meshgrid for feature 1
x1 (np.ndarray): Meshgrid for feature 2
width (int): Width of the plot
height (int): Height of the plot
output (str): File path to save the plot
display (bool): Flag to display the plot
"""
num_plots = len(self.models) + 2
num_panel_rows = num_plots // num_panel_columns
whole_width = width * num_panel_columns
whole_height = height * num_panel_rows
specs = [[{'type': 'surface'} for _ in range(num_panel_columns)] for _ in range(num_panel_rows)]
fig = make_subplots(rows=num_panel_rows, cols=num_panel_columns,
specs=specs, subplot_titles=self.titles,
vertical_spacing=vertical_spacing,
horizontal_spacing=horizontal_spacing)
for i, model in enumerate([None, None] + self.models):
# Assign the subplot panels
row = i // num_panel_columns + 1
col = i % num_panel_columns + 1
# Plot training points
if i == 1:
fig.add_trace(go.Scatter3d(x=self.X_train[:, 0], y=self.X_train[:, 1], z=self.y_train,
mode='markers', marker=dict(size=2, color='darkslategray'),
name='Training Data'), row=row, col=col)
surface = go.Surface(z=self.y_truth, x=x0, y=x1,
showscale=False, opacity=.4)
fig.add_trace(surface, row=row, col=col)
# Plot predicted surface for each model and ground truth
else:
y_pred = self.y_truth if model is None else model.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)
surface = go.Surface(z=y_pred, x=x0, y=x1,
showscale=False)
fig.add_trace(surface, row=row, col=col)
fig.update_scenes(dict(
xaxis_title='x0',
yaxis_title='x1',
zaxis_title='y',
), row=row, col=col)
fig.update_layout(title='Model Predictions and Ground Truth',
width=whole_width,
height=whole_height)
# Change camera angle
camera = dict(
up=dict(x=0, y=0, z=1),
center=dict(x=0, y=0, z=0),
eye=dict(x=-1.25, y=-1.25, z=2)
)
for i in range(num_plots):
fig.update_layout(**{f'scene{i+1}_camera': camera})
if display:
fig.show()
if output:
fig.write_html(output)
if return_fig:
return fig
Evaluation of Interpolation Performance
The prediction surfaces for each algorithm are shown for training data cases of 100 and 20 points respectively.
100 Training Points:
20 Training Points:
Here are the summarized features for each algorithm:
Symbolic Regressor
This algorithm performs almost perfectly in interpolation even with as few as 20 data points. This is because the Symbolic Regressor approximates the mathematical expressions and the simple functional form is used in this practice. Thanks to this feature, the predicted surface is notably smooth which is different from the tree-based algorithms explained later.
Support Vector Regressor (SVR), Gaussian Process Regressor (GPR)
For kernel-based algorithms SVR and GPR, although the predicted surfaces slightly differ from the ground truth, interpolation performance is generally good with 100 data points. In addition, the prediction surface obtained from these models is smooth similar to one estimated by Symbolic Regressor. However, in the case of 20 points, there is a significant difference between the predicted surface and the ground truth especially for SVR.
Decision Tree, Random Forest, XGBoost, LightGBM
Firstly, the prediction surfaces estimated by these five tree-based models are not smooth but more step-like shapes. This characteristic arises from the structure and learning method of decision trees. Decision trees split the data recursively based on a threshold for one of the features. Each data point is assigned to some leaf nodes whose values are represented as the average value of the data points in that node. Therefore, the prediction values are constant within each leaf node, resulting in a step-like prediction surface.
The estimates of a single decision tree clearly show this characteristic. On the other hand, ensemble methods like Random Forests, XGBoost, and LightGBM, which consist of many decision trees within a single model, generate relatively smoother prediction surfaces due to the more different thresholds based on the many different shapes of decision trees.
Voting Regressor, Stacking Regressor
The Voting Regressor combines the results of two algorithms by averaging them. For combinations like Random Forest + SVR, and Random Forest + GPR, the prediction surfaces reflect characteristics that mix the kernel-based and tree-based models. On the other hand, the combination of tree-based models like Random Forest and XGBoost relatively reduces the step-like shape prediction surface than one estimated from the single model.
The Stacking Regressor, which uses a meta-model to compute final predictions based on the outputs of multiple models, also shows step-like surfaces, because of the Random Forest used as the meta-model. This characteristic will be changed if kernel-based algorithms like SVR or GPR are used as the meta-model.
Evaluation of Extrapolation Performance
As explained earlier, each model is trained with data ranging from -0.5 to 1 for both x₀ and x₁ and those performances will be evaluated within the range of -1 to 1. Therefore, we get to know the extrapolation ability to inspect the prediction surface with the range of -1 to -0.5 for both x₀ and x₁.
The prediction surfaces for each algorithm are shown for training data cases of 100 and 20 points respectively.
100 Training Points:
20 Training Points:
Symbolic Regressor
The predicted surface within the area of extrapolation obtained by the Symbolic Regressor which is trained with 100 data points is almost accurately estimated similar to the interpolation evaluation. However, with only 20 training data points used, the predicted surface differs from the ground truth especially in the edge of the surface, indicating that the obtained functional form is not well estimated.
Support Vector Regressor (SVR), Gaussian Process Regressor (GPR)
Although both SVR and GPR are kernel-based algorithms, the obtained results are totally different. For both of 20 and 100 data points, while the predicted surface from SVR is well not estimated, GPR predicts almost perfectly even within the range of extrapolation.
Decision Tree, Random Forest, XGBoost, LightGBM
Although there are some differences among the results from these tree-based models, the predicted surfaces are constant in the range of extrapolation. This is because that decision trees rely on splits and no splits are generated in extrapolation regions, which cause constant values.
Voting Regressor, Stacking Regressor
As seen above, the kernel-based algorithms have better performance compared to the tree-based ones. The Voting Regressor with the combination of Random Forest and XGBoost, and all three Stacking Regressors whose meta-model is Random Forest predict constant in the range of extrapolation. On the other hand, the prediction surfaces derived from the Voting Regressor with the combination of Random Forest + SVR, and Random Forest + GPR have the blended characteristics of kernel-based and tree-based models.
Summary
In this article, we evaluated the interpolation and extrapolation performance of the various machine learning algorithms. Since the ground truth data we used is expressed as a simple functional foam, symbolic regressor and kernel-based algorithms provide a better performance, especially for extrapolation than tree-based algorithms. However, more complex tasks that cannot be expressed in mathematical formulas might bring different results.
Thank you so much for reading this article! I hope this article helps you understand the interpolation and extrapolation performance of machine learning models, making it easier to select and apply the right models for your projects.
Links
Other articles
- How OpenAI’s Sora is Changing the Game: An Insight into Its Core Technologies
- Create “Interactive Globe + Earthquake Plot in Python
- Pandas Cheat Sheet for Data Preprocessing
Personal website
The Machine Learning Guide for Predictive Accuracy: Interpolation and Extrapolation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The Machine Learning Guide for Predictive Accuracy: Interpolation and Extrapolation