The Bias Variance Tradeoff and How it Shapes The LLMs of Today

The Bias Variance Tradeoff and How it Shapes the LLMs of Today

Is low inductive bias essential for building general-purpose AI?

In today’s ML space, we find ourselves surrounded by these massive transformer models like chatGPT and BERT that give us unbeatable performance on just about any downstream task, with the caveat being the requirement of huge amounts of pre-training on upstream tasks first. What makes transformers need so many parameters, and hence, so much training data to make them work?

This is the question I wanted to delve into by exploring the connection between LLMs and the cornerstone topic of bias and variance in data-science. This show be fun!

Background

Firstly, we need to go back down to memory lane and define some ground work for what is to come.

Variance

Variance is almost synonymous with overfitting in data science. The core linguistic choice for the term is the concept of variation. A high variance model is a model whose predicted value for the target variable Y varies greatly when small changes in the input variable X occur.

So in high-variance models, a small change in X, causes a huge response in Y (that’s why Y is usually called a response variable). In the classical example of variance below, you can see this come to light, just by slightly changing X, we immediately get a different Value for Y.

This would also manifest itself in classification tasks in the form of classifying ‘Mr Michael’ as Male, but ‘Mr Miichael’ as female, an immediate and significant response in the output of the neural network that made model change its classification just due to adding one letter.

Bias

Bias is closely related to under-fitting, and the term itself has roots that help explain why it’s used in this context. Bias in general, means to deviate from the real value due to leaning towards something, in ML terms, a High bias model is a model that has bias towards certain features in the data, and chooses to ignore the rest, this is usually caused by under parameterization, where the model does not have enough complexity to accurately fit on the data, so it builds an over simplistic view.

In the image below you can see that the model does not give enough head to the overarching pattern of the data and naively fits to certain data points or features and ignores the parabolic feature or pattern of the data

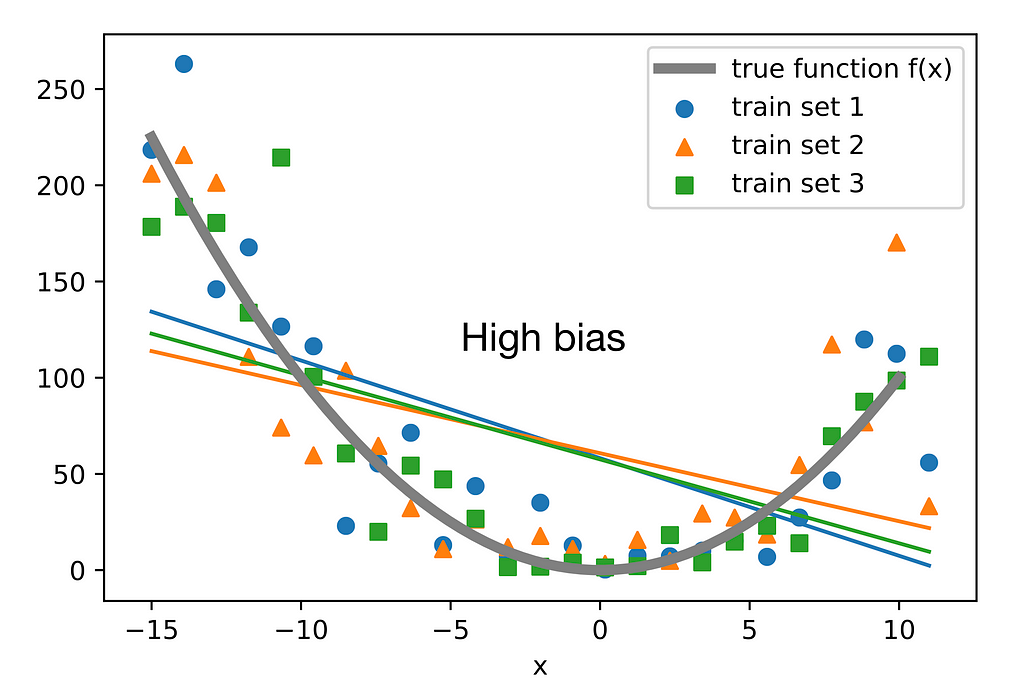
Inductive Bias

Inductive bias is a prior preference for specific rules or functions, and is a specific case of Bias. This can come from prior knowledge about the data, be it using heuristics or laws of nature that we already know. For example: if we want to model radioactive decay, then the curve needs to be exponential and smooth, that is prior knowledge that will affect my model and it’s architecture.

Inductive bias is not a bad thing, if you have a-priori knowledge about your data, you can reach better results with less data, and hence, less parameters.

A model with high inductive bias (that is correct in its assumption) is a model that has much less parameters, yet gives perfect results.

Choosing a neural network for your architecture is equivalent to choosing an explicit inductive bias.

In the case of a model like CNNs, there is implicit bias in the architecture by the usage of filters (feature detectors) and sliding them all over the image. these filters that detect things such as objects, no matter where they are on the image, is an application of a-priori knowledge that an object is the same object regardless of its position in the image, this is the inductive bias of CNNs

Formally this is known as the assumption of Translational Independence, where a feature detector that is used in one part of the image, is probably useful in detecting the same feature in other parts of the image. You can instantly see here how this assumption saves us parameters, we are using the same filter but sliding it around the image instead of perhaps, a different filter for the same feature for the different corners of the image.

Another piece of inductive bias built into CNNs, is the assumption of locality that it is enough to look for features locally in small areas of the image, a single feature detector need not span the entire image, but a much smaller fraction of it, you can also see how this assumption, speeds up CNNs and saves a boatload of parameters. The image below illustrates how these feature detectors slide across the image.

These assumptions come from our knowledge of images and computer graphics. In theory, a dense feed-forward network could learn the same features, but it would require significantly more data, time, and computational resources. We would also need to hope that the dense network makes these assumptions for us, assuming it’s learning correctly.

For RNNs, the theory is much the same, the implicit assumptions here are that the data is tied to each other in the form of temporal sequence, flowing in a certain direction (left to right or right to left). Their gating mechanisms and they way they process sequences makes them biased to short term memory more (one of the main drawbacks of RNNs)

Transformers and their low Inductive Bias

Hopefully after the intensive background we established we can immediately see something different with transformers, their assumptions about the data are little to none (maybe that’s why they’re so useful for so many types of tasks)

The transformer architecture makes no significant assumptions about a sequence. i.e a transformer is good at paying attention to all parts of the input at all times. This flexibility comes from self-attention, allowing them to process all parts of a sequence in parallel and capture dependencies across the entire input. This architectural choice makes transformers effective at generalizing across tasks without assumptions about locality or sequential dependencies.

So we can immediately see here that there are no locality assumptions like CNNs, nor simplistic short term memory bias like RNNs. This is what gives Transformers all their power, they have low inductive bias and make no assumptions about the data, and hence their capability to learn and generalize is great, there are no assumptions that hamper the transformer from deeply understanding the data during pertaining.

The drawback here is obvious, transformers are huge, they have unimaginable amounts of parameters, partially due to the lack of assumptions and inductive bias, and by direct implication, also need copious amounts of data for training, where during training they learn the distribution of the input data perfectly (with a tendency for overfitting since low bias gives rise to high variance). This is why some LLMs simply seem to parrot things they have seen during training. The image illustrates an example of self attention, how transformers consider all other words in a sentence when processing each word, and also when generating new ones.

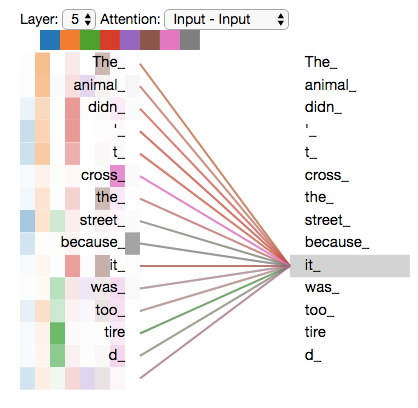
Are transformers really the final frontier of AI? or are there smarter, better solutions that have higher inductive bias just waiting to be explored? This is an open ended question and has no direct answer. Maybe there is an implicit need for low inductive bias in order to have general purpose AI that is good at multiple tasks, or maybe there is a shortcut that we can take along the way that will not hamper how well the model generalizes.

I’ll leave that to your own deliberations as a reader.

Conclusion

In this article we explored the theory of bias from the ground up, how transformers as an architecture is a tool that makes very little assumptions about the data and how to process it, and that is what gives them their excellence over convolutional neural networks and recurrent neural networks, but it is also the reason for its biggest drawback, size and complexity. Hope this article was able to shed light on deep overarching themes in machine learning with a fresh perspective.

The Bias Variance Tradeoff and How it Shapes The LLMs of Today was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.