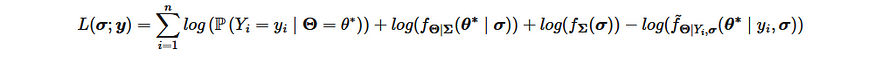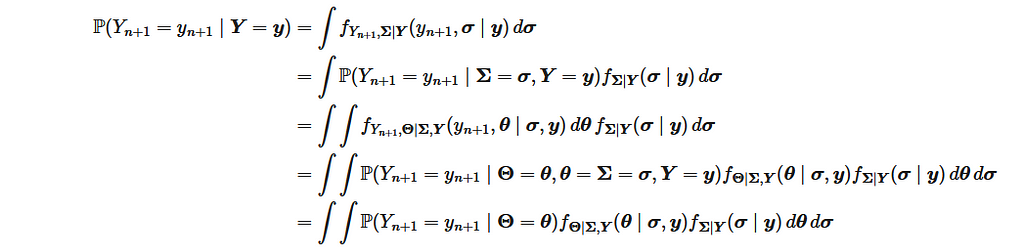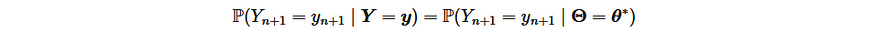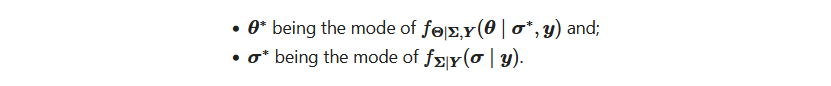Samsung’s big Galaxy S25 launch is right around the corner. The first Galaxy Unpacked event of 2025 is confirmed for January 22 at 1PM ET in San Jose, CA, where Samsung’s “Next Big Thing” (to borrow a 14-year-old marketing slogan) will be revealed. What exactly will be on tap? Well, apart from a few sure bets and some likely leaks, only those sworn to a blood oath under an NDA know for certain. But here are the most likely products and features we’ll see.
Galaxy S25, S25+ and S25 Ultra
Much like Apple reveals its latest iPhones at its first fall event, Samsung typically launches its mainline Galaxy S flagships at its first Unpacked shindig of the year. You can bet the farm that there will be Galaxy S25 phones at this event. And given Samsung’s recent trend of launching three tiers of flagships — standard, Plus and Ultra — you can bet we’ll see that again. (Samsung could technically change the brand names, but the three-layered lineup is practically guaranteed.) There’s even an FCC certification (first spotted by 91Mobiles) to dispel any doubts.
The degree of certainty falls sharply once we dig into the phones’ features. A subtle redesign with rounded corners, flatter edges and thinner bezels appears likely based on a leaked video posted to Reddit and images from reputable tipster Ice Universe. But this isn’t expected to be the generation where Samsung’s hiring of a former Mercedes-Benz designer will lead to drastic aesthetic changes.
At least in the US, the phone is practically guaranteed to use Qualcomm’s Snapdragon 8 Elite processor, which the chip-maker revealed in October. (Qualcomm even listed Samsung among the companies launching devices with that processor “in the coming weeks.”) Like just about every flagship processor these days, the Snapdragon 8 Elite is built for on-device generative AI, which aligns with Samsung’s Galaxy AI blitz in recent models.
We don’t know whether the company will split its S25 processors between Snapdragon (US and other markets) and Exynos (everywhere else), but Ice Universe has claimed it will be all Snapdragon this generation. That would be a good thing, given what’s often a glaring performance and battery life disparity favoring Qualcomm.
The phone will run Samsung’s One UI 7 on top of Android 15. We know this because Samsung said in October that its user experience (based on Android 15) will launch on the next Galaxy S flagships. It’s already available in beta for Galaxy S24 phones.
Samsung is rumored to stick with last-generation OLED displays (made with M13 organic materials) instead of the brighter and more efficient M14 OLED panels used in the iPhone 16 Pro and Google Pixel 9. Logic suggests Samsung would want its best homemade screen in its best phones — especially when its competitors are already using it. But it could stick with the cheaper panels to keep the bill of materials down. Perhaps it calculated that better displays don’t make for better generative AI (the obsession of nearly every tech company right now), while the latest Qualcomm chip does.
Speaking of AI, expect Samsung to devote a perhaps agonizingly long portion of the event to generative AI features. The hit-or-miss DigiTimes reported last month that the Galaxy S25 series will include “an AI Agent that provides personalized clothing suggestions and transport information.” What that would look like in practice is anyone’s guess, but I’m not sure I want to know.
On the camera front, Ice Universe claims (via Android Headlines) it’s “confirmed” that only the ultra-wide sensor will see an upgrade in the Galaxy S25 Ultra — to 50MP from 12MP in last year’s model. The leaker says the S25 Ultra will stick with a 200MP main sensor, 10MP 3x zoom and 50MP 5x zoom.
Samsung will add the Qi2 wireless charging standard to its new flagships — and that comes straight from the horse’s (aka, the Wireless Power Consortium’s) mouth. However, leaker chunvn8888 (aka “yawn”) says Samsung’s phones won’t have built-in magnets for Qi2’s native MagSafe in everything but name charging. Instead, the leaker says Samsung will sell a first-party case with a Qi2 magnetic ring to enable that. (Gotta move those accessories, baby!)
Rumors have buzzed about an alleged Galaxy S25 Slim with a — you guessed it — slimmer design joining the trio at some point this year. That’s something Apple is also rumored to be working on. However, given the FCC certifications only appear to cover the familiar trio of flagships, that phone (if it’s in the pipeline at all) may not arrive until later in the year.
Galaxy Ring 2, Samsung XR and AR glasses
DigiTimes reported in December that Samsung would show off (or maybe just tease) the Galaxy Ring 2 and augmented reality (AR) glasses during its January Unpacked event.
The Taiwanese publication says the Galaxy Ring 2 will add two more sizes to the nine from the original model, which only launched in July. The second-gen wearable health tracker is said to add new AI features (surprise!) and updated sensors for more accurate measurements. The Galaxy Ring 2 is also rumored to last longer than the current model’s maximum of seven days.
DigiTimes also claims Samsung’s AR glasses — which the company has confirmed it’s working on — will look like regular prescription glasses and weigh around 50g. It says the futuristic glasses would use Google’s Gemini AI, which aligns with what we already know about Samsung’s partnership with Google and Qualcomm on Android XR. But given the lack of supply chain rumors surrounding the glasses, it’s likely that any mention at the event would amount to little more than a teaser, a la its grand reveal of… a stinkin’ render for the first Galaxy Ring at Unpacked 2024.
We also know Samsung is co-developing an Android XR (extended reality) headset — codenamed Project Moohan — alongside Google and Qualcomm. The “lightweight” and “ergonomically designed” headset will have a “state-of-the-art display,” passthrough video and natural multi-modal input. Google’s renderings show a wearable reminiscent of Apple’s $3,500 Vision Pro.
Since Google only recently began offering a developer kit and API for the platform, any glimpse of it at Unpacked wouldn’t likely include an imminent release or deep dive into its hardware.
Engadget will have full coverage of Samsung’s first Unpacked event of 2025. More to come on January 22!
This article originally appeared on Engadget at https://www.engadget.com/mobile/smartphones/what-to-expect-at-samsungs-galaxy-s25-unpacked-event-182028420.html?src=rss
Go Here to Read this Fast! What to expect at Samsung’s Galaxy S25 Unpacked event
Originally appeared here:
What to expect at Samsung’s Galaxy S25 Unpacked event