Instance Selection for Deep Learning — Part 2

This post was written in collaboration with Tomer Berkovich, Yitzhak Levi, and Max Rabin.
Appropriate instance selection for machine learning (ML) workloads is an important decision with potentially significant implications on the speed and cost of development. In a previous post we expanded on this process, proposed a metric for making this important decision, and highlighted some of the many factors you should take into consideration. In this post we will demonstrate the opportunity for reducing AI model training costs by taking Spot Instance availability into account when making your cloud-based instance selection decision.
Reducing Costs Using Spot Instances
One of the most significant opportunities for cost savings in the cloud is to take advantage of low cost Amazon EC2 Spot Instances. Spot instances are discounted compute engines from surplus cloud service capacity. In exchange for the discounted price, AWS maintains the right to preempt the instance with little to no warning. Consequently, the relevance of Spot instance utilization is limited to workloads that are fault tolerant. Fortunately, through effective use of model checkpointing ML training workloads can be designed to be fault tolerant and to take advantage of the Spot instance offering. In fact, Amazon SageMaker, AWS’s managed service for developing ML, makes it easy to train on Spot instances by managing the end-to-end Spot life-cycle for you.
The Challenge of Anticipating Spot Instance Capacity
Unfortunately, Spot instance capacity, which measures the availability of Spot instances for use, is subject to constant fluctuations and can be very difficult to predict. Amazon offers partial assistance in assessing the Spot instance capacity of an instance type of choice via its Spot placement score (SPS) feature which indicates the likelihood that a Spot request will succeed in a given region or availability zone (AZ). This is especially helpful when you have the freedom to choose to train your model in one of several different locations. However, the SPS feature offers no guarantees.
When you choose to train a model on one or more Spot instances, you are taking the risk that your instance type of choice does not have any Spot capacity (i.e., your training job will not start), or worse, that you will enter an iterative cycle in which your training repeatedly runs for just a small number of training steps and is stopped before you have made any meaningful progress — which can tally up your training costs without any return.
Over the past couple of years, the challenges of spot instance utilization have been particularly acute when it comes to multi-GPU EC2 instance types such as g5.12xlarge and p4d.24xlarge. A huge increase in demand for powerful training accelerators (driven in part by advances in the field of Generative AI) combined with disruptions in the global supply chain, have made it virtually impossible to reliably depend on multi-GPU Spot instances for ML training. The natural fallback is to use the more costly On-Demand (OD) or reserved instances. However, in our previous post we emphasized the value of considering many different alternatives for your choice of instance type. In this post we will demonstrate the potential gains of replacing multi-GPU On Demand instances with multiple single-GPU Spot instances.
Although our demonstration will use Amazon Web Services, similar conclusions can be reached on alternative cloud service platforms (CSPs). Please do not interpret our choice of CSP or services as an endorsement. The best option for you will depend on the unique details of your project. Furthermore, please take into consideration the possibility that the type of cost savings we will demonstrate will not reproduce in the case of your project and/or that the solution we propose will not be applicable (e.g., for some reason beyond the scope of this post). Be sure to conduct a detailed evaluation of the relevance and efficacy of the proposal before adapting it to your use case.
When Multiple Single-GPU Instances are Better than a Single Multi-GPU Instance
Nowadays, training AI models on multiple GPU devices in parallel — a process called distributed training — is commonplace. Setting aside instance pricing, when you have the choice between an instance type with multiple GPUs and multiple instance types with the same type of single GPUs, you would typically choose the multi-GPU instance. Distributed training typically requires a considerable amount of data communication (e.g., gradient sharing) between the GPUs. The proximity of the GPUs on a single instance is bound to facilitate higher network bandwidth and lower latency. Moreover, some multi-GPU instances include dedicated GPU-to-GPU inter-connections that can further accelerate the communication (e.g., NVLink on p4d.24xlarge). However, when Spot capacity is limited to single GPU instances, the option of training on multiple single GPU instances at a much lower cost becomes more compelling. At the very least, it warrants evaluation of its opportunity for cost-savings.
Optimizing Data Communication Between Multiple EC2 Instances
When distributed training runs on multiple instances, the GPUs communicate with one another via the network between the host machines. To optimize the speed of training and reduce the likelihood and/or impact of a network bottleneck, we need to ensure minimal network latency and maximal data throughput. These can be affected by a number of factors.
Instance Collocation
Network latency can be greatly impacted by the relative locations of the EC2 instances. Ideally, when we request multiple cloud-based instances we would like them to all be collocated on the same physical rack. In practice, without appropriate configuration, they may not even be in the same city. In our demonstration below we will use a VPC Config object to program an Amazon SageMaker training job to use a single subnet of an Amazon Virtual Private Cloud (VPC). This technique will ensure that all the requested training instances will be in the same availability zone (AZ). However, collocation in the same AZ, may not suffice. Furthermore, the method we described involves choosing a subnet associated with one specific AZ (e.g., the one with the highest Spot placement score). A preferred API would fulfill the request in any AZ that has sufficient capacity.
A better way to control the placement of our instances is to launch them inside a placement group, specifically a cluster placement group. Not only will this guarantee that all of the instances will be in the same AZ, but it will also place them on “the same high-bisection bandwidth segment of the network” so as to maximize the performance of the network traffic between them. However, as of the time of this writing SageMaker does not provide the option to specify a placement group. To take advantage of placement groups we would need to use an alternative training service solution (as we will demonstrate below).
EC2 Network Bandwidth Constraints
Be sure to take into account the maximal network bandwidth supported by the EC2 instances that you choose. Note, in particular, that the network bandwidths associated with single-GPU machines are often documented as being “up to” a certain number of Gbps. Make sure to understand what that means and how it can impact the speed of training over time.
Keep in mind that the GPU-to-GPU data communication (e.g., gradient sharing) might need to share the limited network bandwidth with other data flowing through the network such as training samples being streamed into the training instances or training artifacts being uploaded to persistent storage. Consider ways of reducing the payload of each of the categories of data to minimize the likelihood of a network bottleneck.
Elastic Fabric Adapter (EFA)
A growing number of EC2 instance types support Elastic Fabric Adapter (EFA), a dedicated network interface for optimizing inter-node communication. Using EFA can have a decisive impact on the runtime performance of your training workload. Note that the bandwidth on the EFA network channel is different than the documented bandwidth of the standard network. As of the time of this writing, detailed documentation of the EFA capabilities is hard to come by and it is usually best to evaluate its impact through trial and error. Consider using an EC2 instance that supports EFA type when relevant.
Toy Example
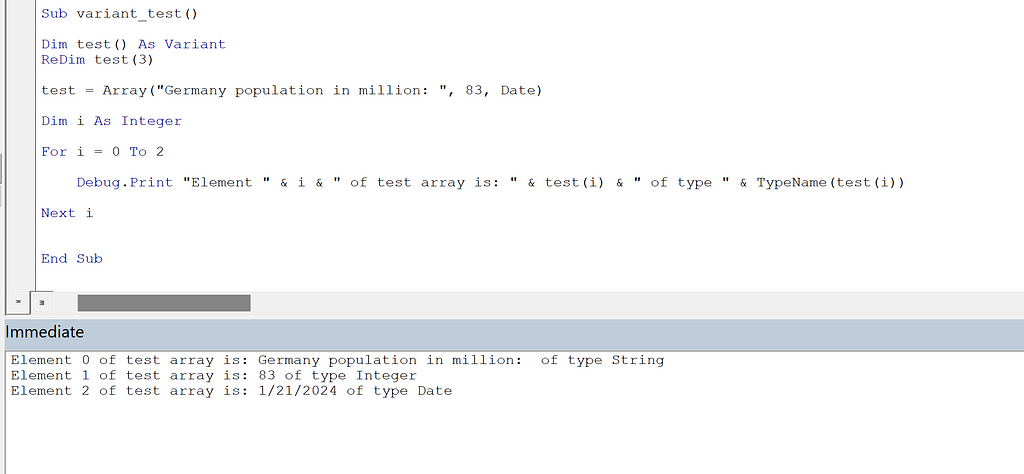
We will now demonstrate the comparative price performance of training on four single-GPU EC2 g5 Spot instances (ml.g5.2xlarge and ml.g5.4xlarge) vs. a single four-GPU On-Demand instance (ml.g5.12xlarge). We will use the training script below containing a Vision Transformer (ViT) backed classification model (trained on synthetic data).
import os, torch, time
import torch.distributed as dist
from torch.utils.data import Dataset, DataLoader
from torch.cuda.amp import autocast
from torch.nn.parallel import DistributedDataParallel as DDP
from timm.models.vision_transformer import VisionTransformer
batch_size = 128
log_interval = 10
# use random data
class FakeDataset(Dataset):
def __len__(self):
return 1000000
def __getitem__(self, index):
rand_image = torch.randn([3, 224, 224], dtype=torch.float32)
label = torch.tensor(data=[index % 1000], dtype=torch.int64)
return rand_image, label
def mp_fn():
local_rank = int(os.environ['LOCAL_RANK'])
dist.init_process_group("nccl")
torch.cuda.set_device(local_rank)
# model definition
model = VisionTransformer()
loss_fn = torch.nn.CrossEntropyLoss()
model.to(torch.cuda.current_device())
model = DDP(model)
optimizer = torch.optim.Adam(params=model.parameters())
# dataset definition
num_workers = os.cpu_count()//int(os.environ['LOCAL_WORLD_SIZE'])
dl = DataLoader(FakeDataset(), batch_size=batch_size, num_workers=num_workers)
model.train()
t0 = time.perf_counter()
for batch_idx, (x, y) in enumerate(dl, start=1):
optimizer.zero_grad(set_to_none=True)
x = x.to(torch.cuda.current_device())
y = torch.squeeze(y.to(torch.cuda.current_device()), -1)
with autocast(enabled=True, dtype=torch.bfloat16):
outputs = model(x)
loss = loss_fn(outputs, y)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0 and local_rank == 0:
time_passed = time.perf_counter() - t0
samples_processed = dist.get_world_size() * batch_size * log_interval
print(f'{samples_processed / time_passed} samples/second')
t0 = time.perf_counter()
if __name__ == '__main__':
mp_fn()
The code block below demonstrates how we used the SageMaker Python package (version 2.203.1) to run our experiments. Note that for the four-instance experiments, we configure the use of a VPC with a single subnet, as explained above.
from sagemaker.pytorch import PyTorch
from sagemaker.vpc_utils import VPC_CONFIG_DEFAULT
# Toggle flag to switch between multiple single-GPU nodes and
# single multi-GPU node
multi_inst = False
inst_count=1
inst_type='ml.g5.12xlarge'
use_spot_instances=False
max_wait=None #max seconds to wait for Spot job to complete
subnets=None
security_group_ids=None
if multi_inst:
inst_count=4
inst_type='ml.g5.4xlarge' # optinally change to ml.g5.2xlarge
use_spot_instances=True
max_wait=24*60*60 #24 hours
# configure vpc settings
subnets=['<VPC subnet>']
security_group_ids=['<Security Group>']
estimator = PyTorch(
role='<sagemaker role>',
entry_point='train.py',
source_dir='<path to source dir>',
instance_type=inst_type,
instance_count=inst_count,
framework_version='2.1.0',
py_version='py310',
distribution={'torch_distributed': {'enabled': True}},
subnets=subnets,
security_group_ids=security_group_ids,
use_spot_instances=use_spot_instances,
max_wait=max_wait
)
# start job
estimator.fit()
Note that our code depends on the third-party timm Python package that we point to in a requirements.txt file in the root of the source directory. This assumes that the VPC has been configured to enable internet access. Alternatively, you could define a private PyPI server (as described here), or create a custom image with your third party dependencies preinstalled (as described here).
Results
We summarize the results of our experiment in the table below. The On-Demand prices were taken from the SageMaker pricing page (as of the time of this writing, January 2024). The Spot saving values were collected from the reported managed spot training savings of the completed job. Please see the EC2 Spot pricing documentation to get a sense for how the reported Spot savings are calculated.

Our results clearly demonstrate the potential for considerable savings when using four single-GPU Spot instances rather than a single four-GPU On Demand instance. They further demonstrate that although the cost of an On Demand g5.4xlarge instance type is higher, the increased CPU power and/or network bandwidth combined with higher Spot savings, resulted in much greater savings.
Importantly, keep in mind that the relative performance results can vary considerably based on the details of your job as well the Spot prices at the time that you run your experiments.
Enforcing EC2 Instance Co-location Using a Cluster Placement Group
In a previous post we described how to create a customized managed environment on top of an unmanaged service, such as Amazon EC2. One of the motivating factors listed there was the desire to have greater control over device placement in a multi-instance setup, e.g., by using a cluster placement group, as discussed above. In this section, we demonstrate the creation of a multi-node setup using a cluster placement group.
Our code assumes the presence of a default VPC as well as the (one-time) creation of a cluster placement group, demonstrated here using the AWS Python SDK (version 1.34.23):
import boto3
ec2 = boto3.client('ec2')
ec2.create_placement_group(
GroupName='cluster-placement-group',
Strategy='cluster'
)
In the code block below we use the AWS Python SDK to launch our Spot instances:
import boto3
ec2 = boto3.resource('ec2')
instances = ec2.create_instances(
MaxCount=4,
MinCount=4,
ImageId='ami-0240b7264c1c9e6a9', # replace with image of choice
InstanceType='g5.4xlarge',
Placement={'GroupName':'cluster-placement-group'},
InstanceMarketOptions={
'MarketType': 'spot',
'SpotOptions': {
"SpotInstanceType": "one-time",
"InstanceInterruptionBehavior": "terminate"
}
},
)
Please see our previous post for step-by-step tips on how to extend this to an automated training solution.
Summary
In this post, we have illustrated how demonstrating flexibility in your choice of training instance type can increase your ability to leverage Spot instance capacity and reduce the overall cost of training.
As the sizes of AI models continue to grow and the costs of AI training accelerators continue to rise, it becomes increasingly important that we explore ways to mitigate training expenses. The technique outlined here is just one among several methods for optimizing cost performance. We encourage you to explore our previous posts for insights into additional opportunities in this realm.
Optimizing Instance Type Selection for AI Development in Cloud Spot Markets was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Optimizing Instance Type Selection for AI Development in Cloud Spot Markets