
Originally appeared here:
Discover insights from Box with the Amazon Q Box connector
Go Here to Read this Fast! Discover insights from Box with the Amazon Q Box connector


Originally appeared here:
Discover insights from Box with the Amazon Q Box connector
Go Here to Read this Fast! Discover insights from Box with the Amazon Q Box connector

Originally appeared here:
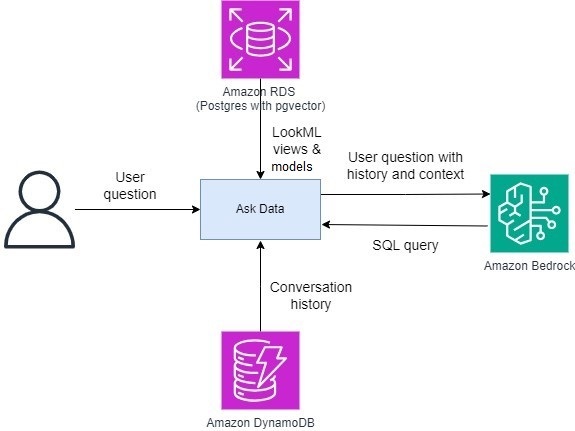
How Twilio generated SQL using Looker Modeling Language data with Amazon Bedrock
Feeling inspired to write your first TDS post? We’re always open to contributions from new authors.
The constant flow of model releases, new tools, and cutting-edge research can make it difficult to pause for a few minutes and reflect on AI’s big picture. What are the questions that practitioners are trying to answer—or, at least, need to be aware of? What does all the innovation actually mean for the people who work in data science and machine learning, and for the communities and societies that these evolving technologies stand to shape for years to come?
Our lineup of standout articles this week tackle these questions from multiple angles—from the business models supporting (and sometimes generating) the buzz behind AI to the core goals that models can and cannot achieve. Ready for some thought-provoking discussions? Let’s dive in.

Looking for other questions to explore this week—whether big, mid-sized, or extremely focused? We invite you to explore some of our other recent standouts.
Thank you for supporting the work of our authors! We love publishing articles from new authors, so if you’ve recently written an interesting project walkthrough, tutorial, or theoretical reflection on any of our core topics, don’t hesitate to share it with us.
Until the next Variable,
TDS Team
The Big Questions Shaping AI Today was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The Big Questions Shaping AI Today
Go Here to Read this Fast! The Big Questions Shaping AI Today
How to get near-perfect LLM performance even with ambiguous user inputs
Originally appeared here:
5 Proven Query Translation Techniques To Boost Your RAG Performance
Go Here to Read this Fast! 5 Proven Query Translation Techniques To Boost Your RAG Performance


An Introductory Guide and Use Case for Applied Data Science
Originally appeared here:
How to Use Machine Learning to Inform Design Decisions and Make Predictions
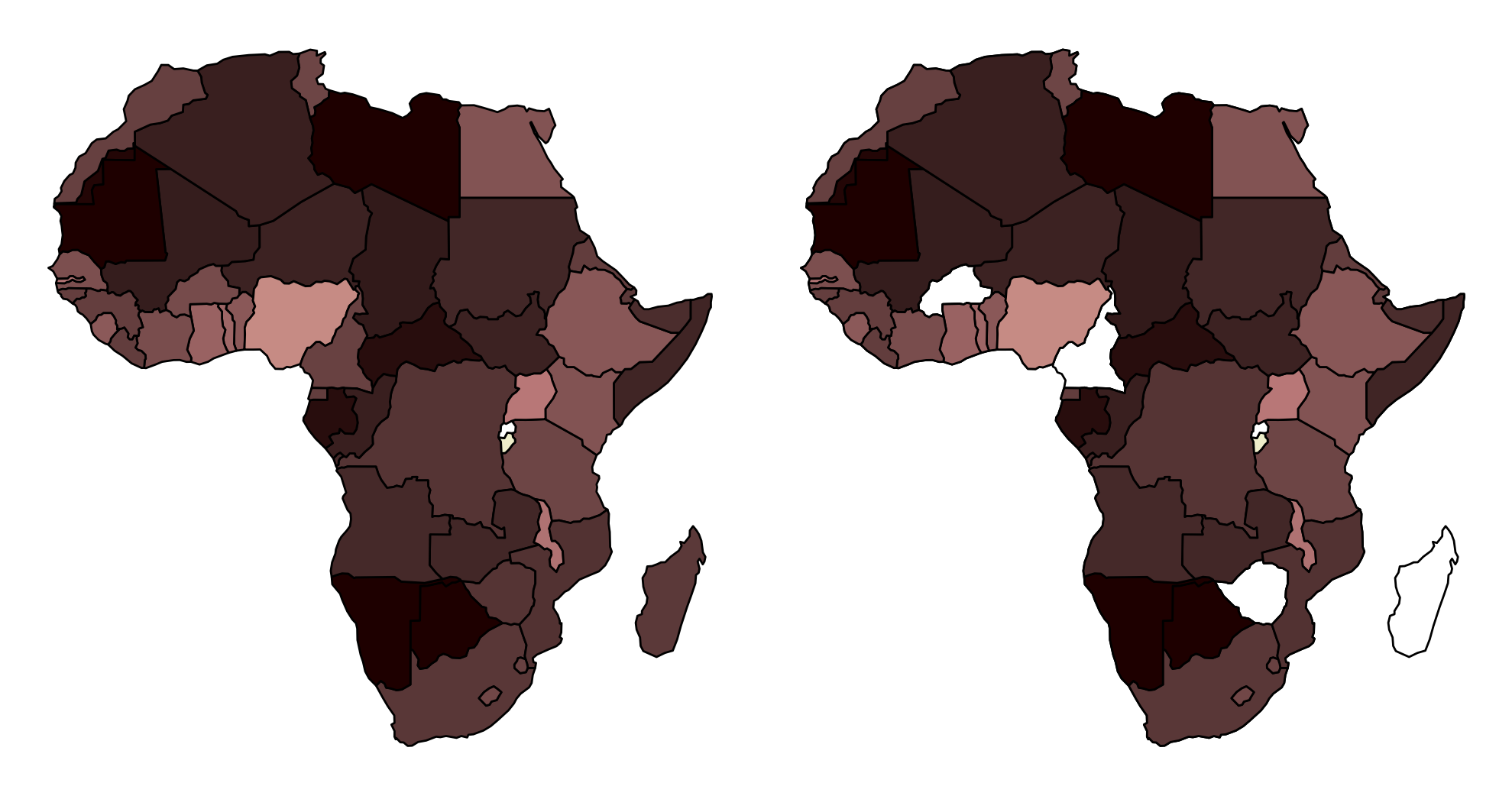
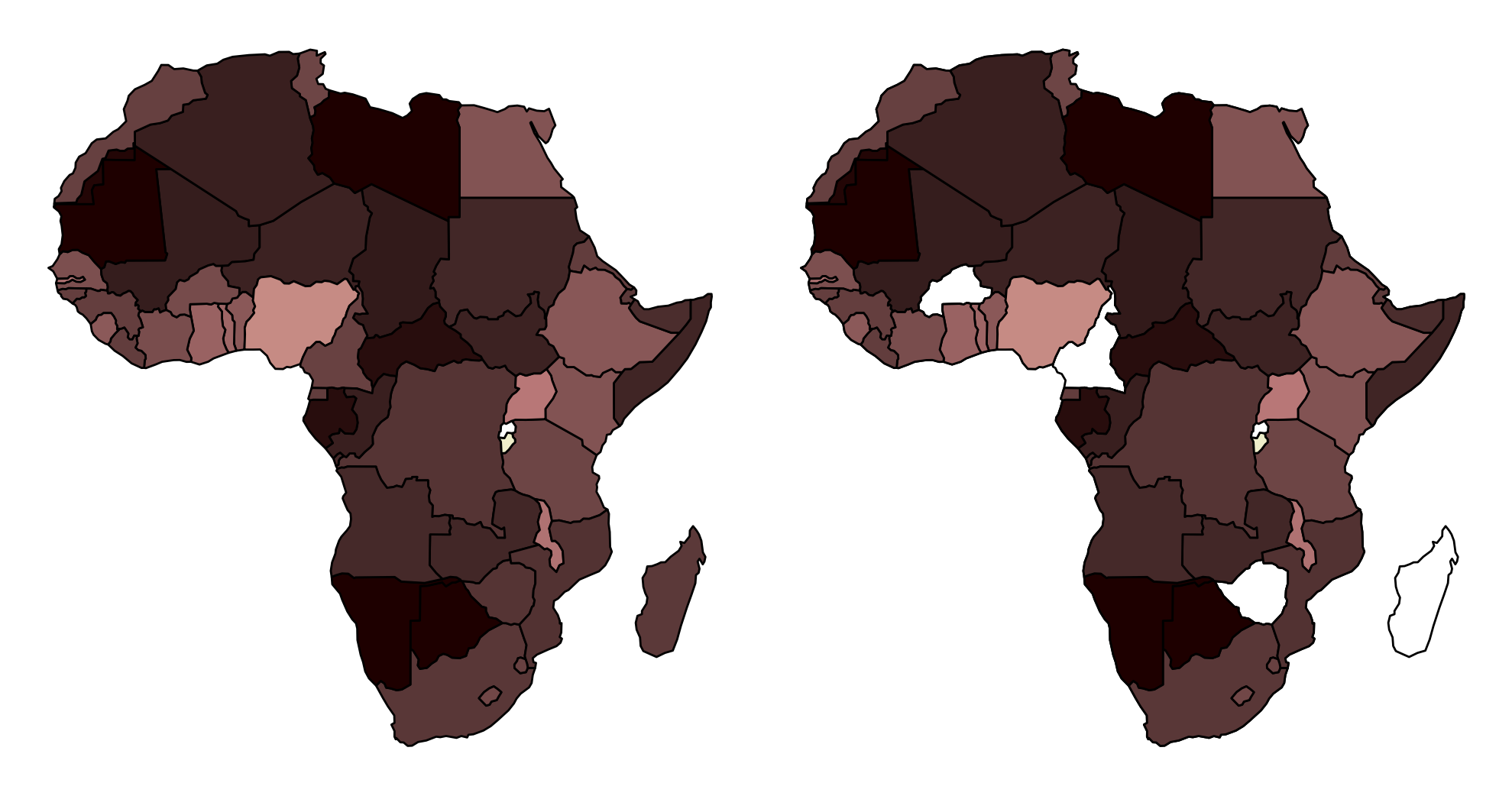
Using the Inverse Distance Weighting method to infer missing spatial data
Originally appeared here:
Spatial Interpolation in Python


What you can do with only 2×24 GB GPUs and a lot of CPU RAM
Originally appeared here:
Multi-GPU Fine-tuning for Llama 3.1 70B with FSDP and QLoRA
Go Here to Read this Fast! Multi-GPU Fine-tuning for Llama 3.1 70B with FSDP and QLoRA
Do you like riddles? Perfect! In this article I’ll use a riddle as a fun way to explain class imbalance bias in machine learning models
Originally appeared here:
How to Reduce Class Imbalance Bias in AI? (Explained with a Riddle)
Go Here to Read this Fast! How to Reduce Class Imbalance Bias in AI? (Explained with a Riddle)


Reinforcement learning is a domain in machine learning that introduces the concept of an agent learning optimal strategies in complex environments. The agent learns from its actions, which result in rewards, based on the environment’s state. Reinforcement learning is a challenging topic and differs significantly from other areas of machine learning.
What is remarkable about reinforcement learning is that the same algorithms can be used to enable the agent adapt to completely different, unknown, and complex conditions.
Note. To fully understand the concepts included in this article, it is highly recommended to be familiar with the basics of Monte Carlo methods and temporal difference learning introduced in the previous articles.
In the previous part, we analyzed how TD algorithms work by combining principles of dynamic programming and MC methods. In addition, we looked at a one-step TD algorithm — the simplest TD implementation. In this article, we will generalize TD concepts and see when it may be advantageous to use other algorithm variants.
This article is based on Chapter 7 of the book “Reinforcement Learning” written by Richard S. Sutton and Andrew G. Barto. I highly appreciate the efforts of the authors who contributed to the publication of this book.
Let us pause for a second and understand what one-step TD and MC algorithms have in common. If we omit overly specific details, we will notice that both of them are actually very similar and use the same state update rule except for a single difference:
We have two extreme cases where n = 1 and where n = the number of remaining states in the episode sequence. A logical question arises: could we use a value of n that falls somewhere in the middle of these extreme values?
The answer is yes. And this concept is generalized through n-step Bootstrapping.

In one-step TD, we analyze the difference between the received reward and how the state value changes by switching from the current state to the next (n = 1). This idea can be easily generalized to multiple steps. To do this, let us introduce the n-step return, which calculates the accumulated discounted reward between the current state t and the future state at step t + n. In addition, it also adds state value at step t + n.

Using the analogous update rule introduced in previous articles, this time we can compare an n-step return with the current state value and derive a new update rule:
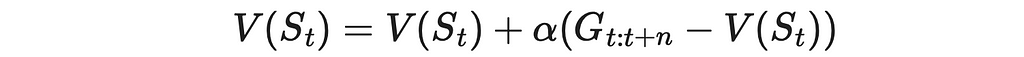
To better understand the workflow, let us draw a diagram of state relationships for several values of n. The diagram below demonstrates how information about next states and rewards is used to update previous states in the sequence.

For instance, let us take the case of 3-step TD:
If for a given state, there are fewer than n states left to calculate the n-step return, then the truncated n-step return is used instead, accumulating available rewards until the terminal state.
If n = ∞, then n-step TD is a Monte Carlo algorithm.
In part 5, we discussed Sarsa, Q-learning and Expected Sarsa algorithms. All of them were based on using information from the next state. As we have already done in this article, we can expand this idea to n-step learning. To achieve this, the only change that needs to be made is to adjust their update formulas to use information not from the next state but from n steps later. Everything else will remain the same.
In part 5, we also highlighted the advantages of one-step TD algorithms over MC methods and how they lead to faster convergence. If so, why not always use one-step TD instead of n-step methods? As it turns out in practice, n = 1 is not always optimal value. Let us look at an example provided by Richard S. Sutton and Andrew G. Barto’s RL book. This example shows a situation where using larger values of n optimizes the learning process.
The image below shows a path made by the agent in a given maze during the first episode of the Sarsa algorithm. The agent’s goal is to find the shortest path to X. When the agent steps on X, it receives a reward R = 1. Every other step made in the maze results in a reward R = 0.

Let us now compare how the agent learns in 1-step Sarsa and 10-step Sarsa. We will assume that all action values are initialised to 0.
In 1-step Sarsa, for every move, the update is performed based only on the information from the next state. This means the only action value with a meaningful update is the one that leads directly to the goal X in a single step. In this case, the agent receives a positive reward and thus learns that making the “up” final move is indeed an optimal decision. However, all other updates do not make any impact because the received reward R = 0 does not change any action values.
On the other hand, in 10-step Sarsa, the final move will propagate its positive reward to the action values for the last 10 moves. In this way, the agent will learn much more information from the episode.

Therefore, in these maze settings, the larger values of n would make the agent learn faster.
Having looked at this example, we can conclude an important fact:
The best value of n in temporal difference learning is problem-dependent.
The generalization of one-step TD and Monte Carlo methods into n-step algorithms plays an important role in reinforcement learning as the best value of n usually lies between these two extremes.
Apart from this, there is no general rule for choosing the best value of n since every problem is unique. While larger values of n lead to more delayed updates, they can still perform better than smaller ones. Ideally one should treat n as a hyperparameter and carefully select it to find the optimum.
All images unless otherwise noted are by the author.
Reinforcement Learning, Part 6: n-step Bootstrapping was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Reinforcement Learning, Part 6: n-step Bootstrapping
Go Here to Read this Fast! Reinforcement Learning, Part 6: n-step Bootstrapping