Tag: AI

Posted by Nishant Jain, Pre-doctoral Researcher, and Pradeep Shenoy, Research Scientist, Google Research

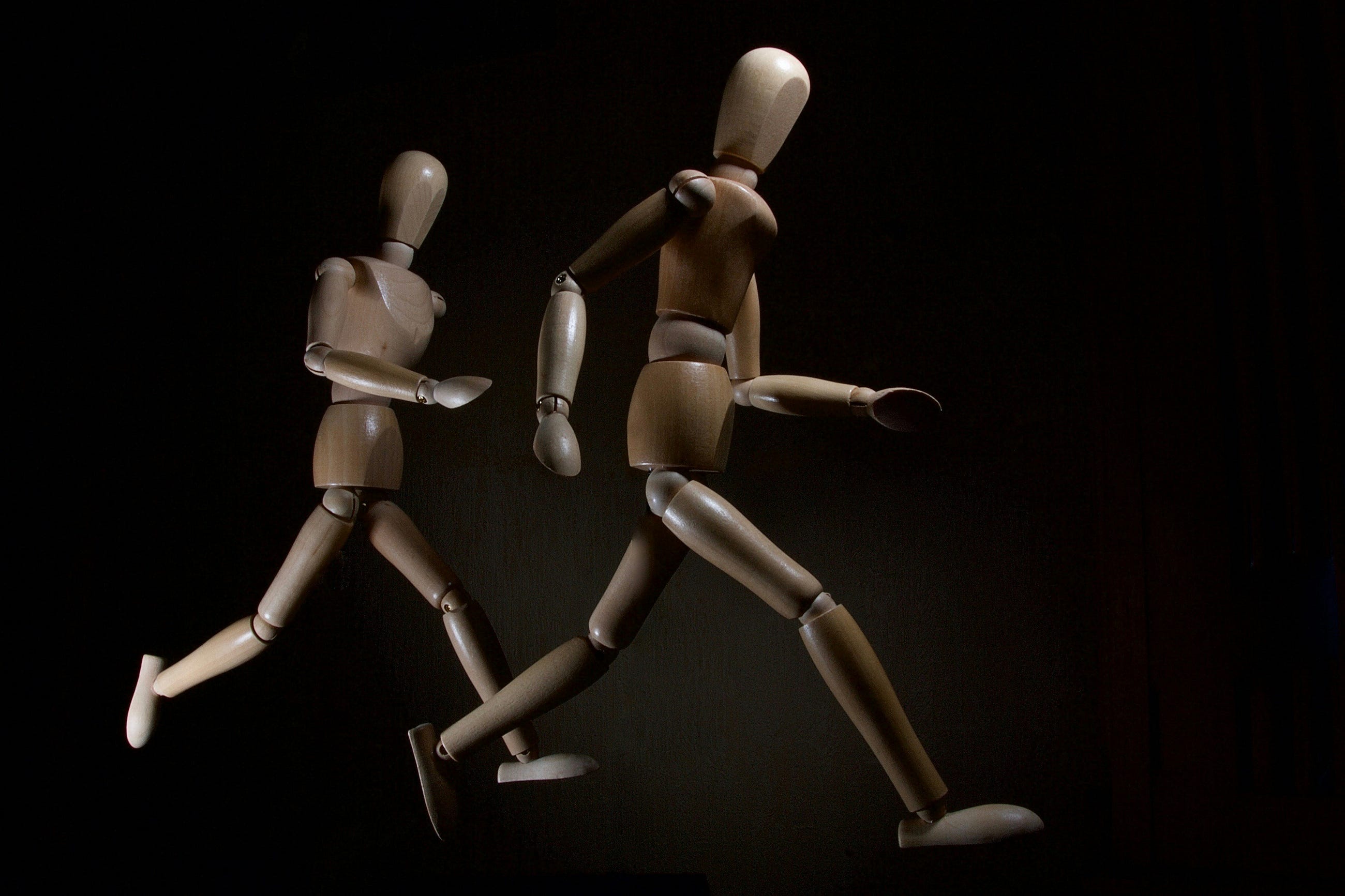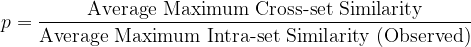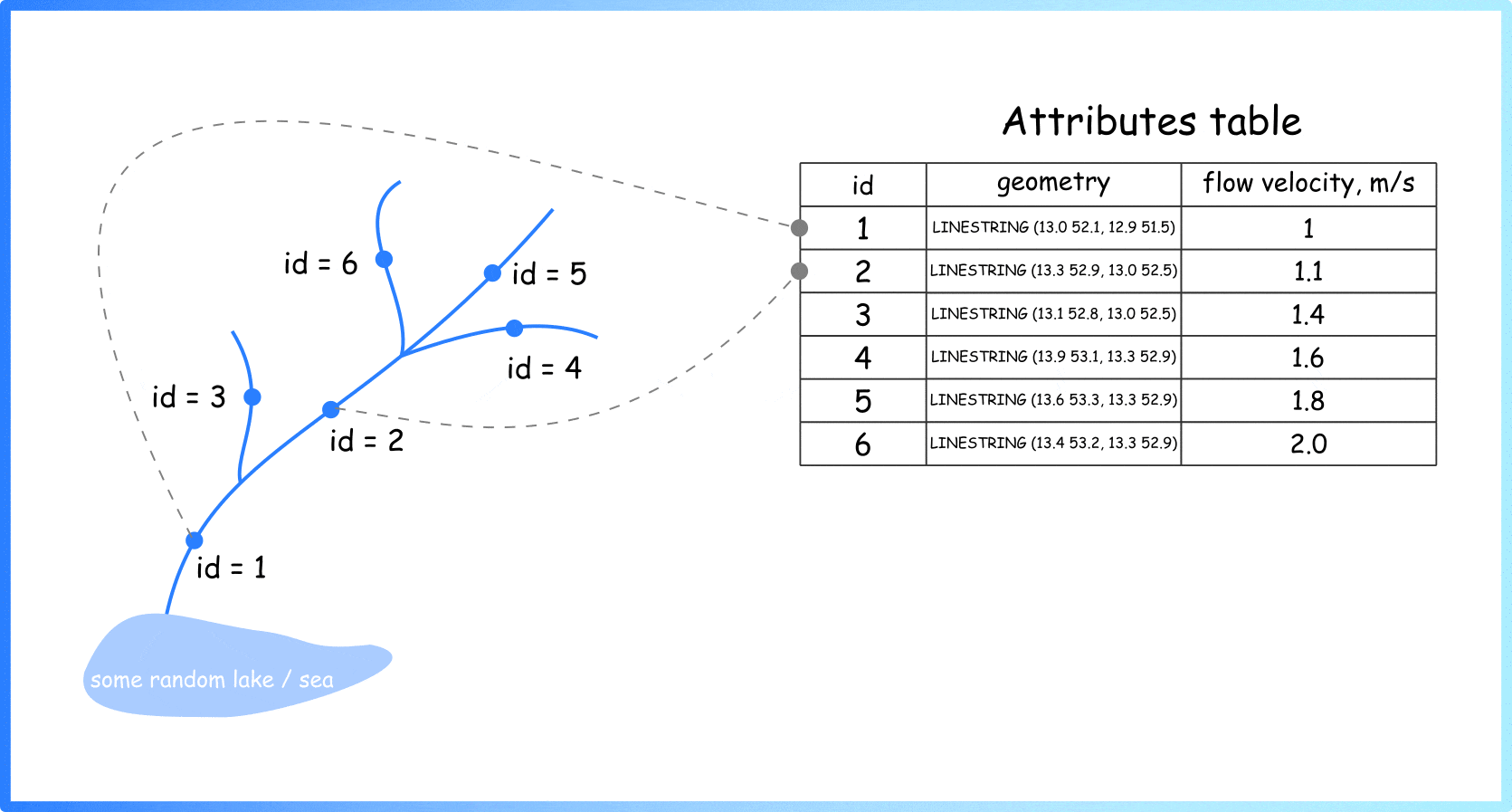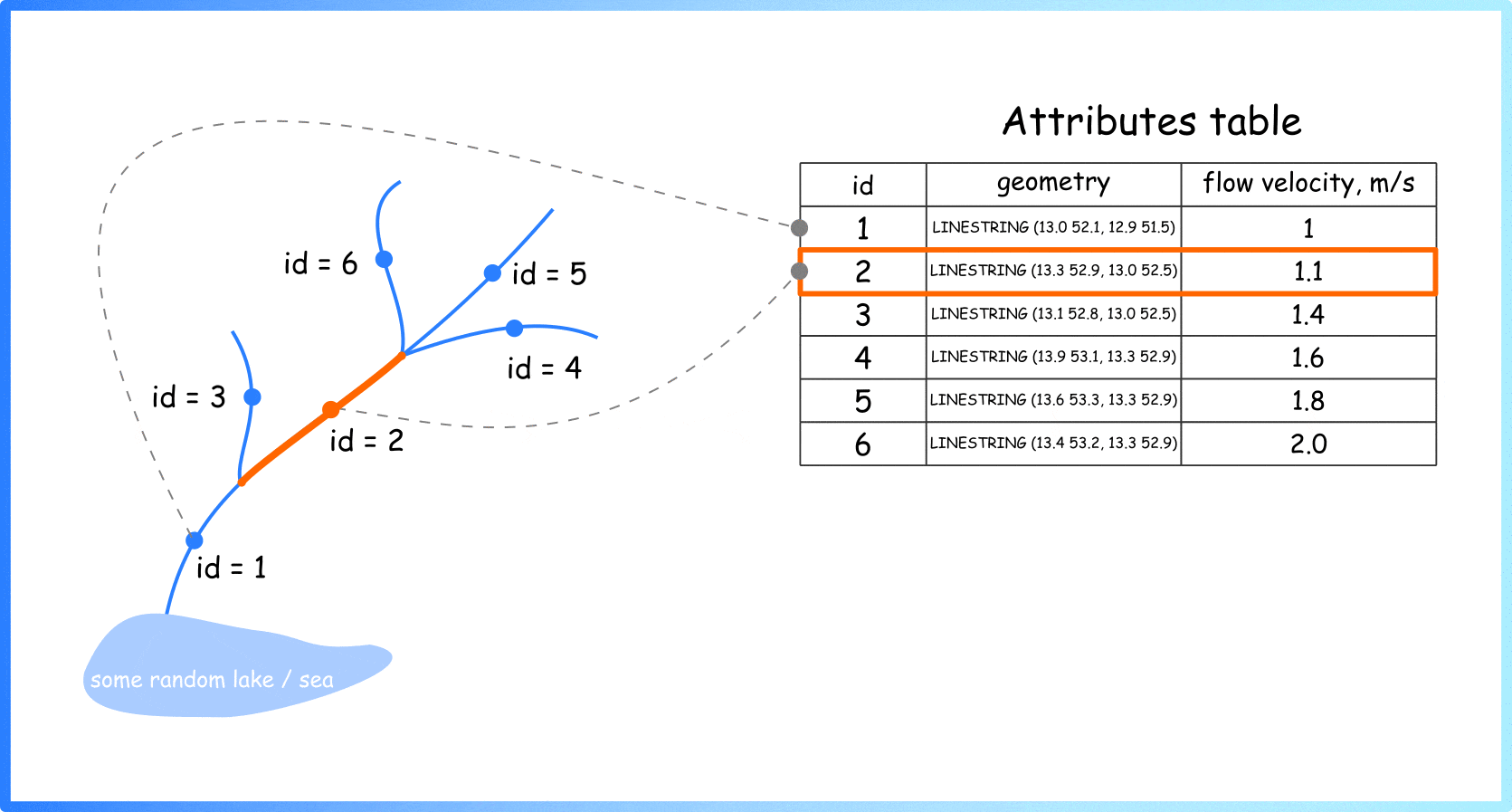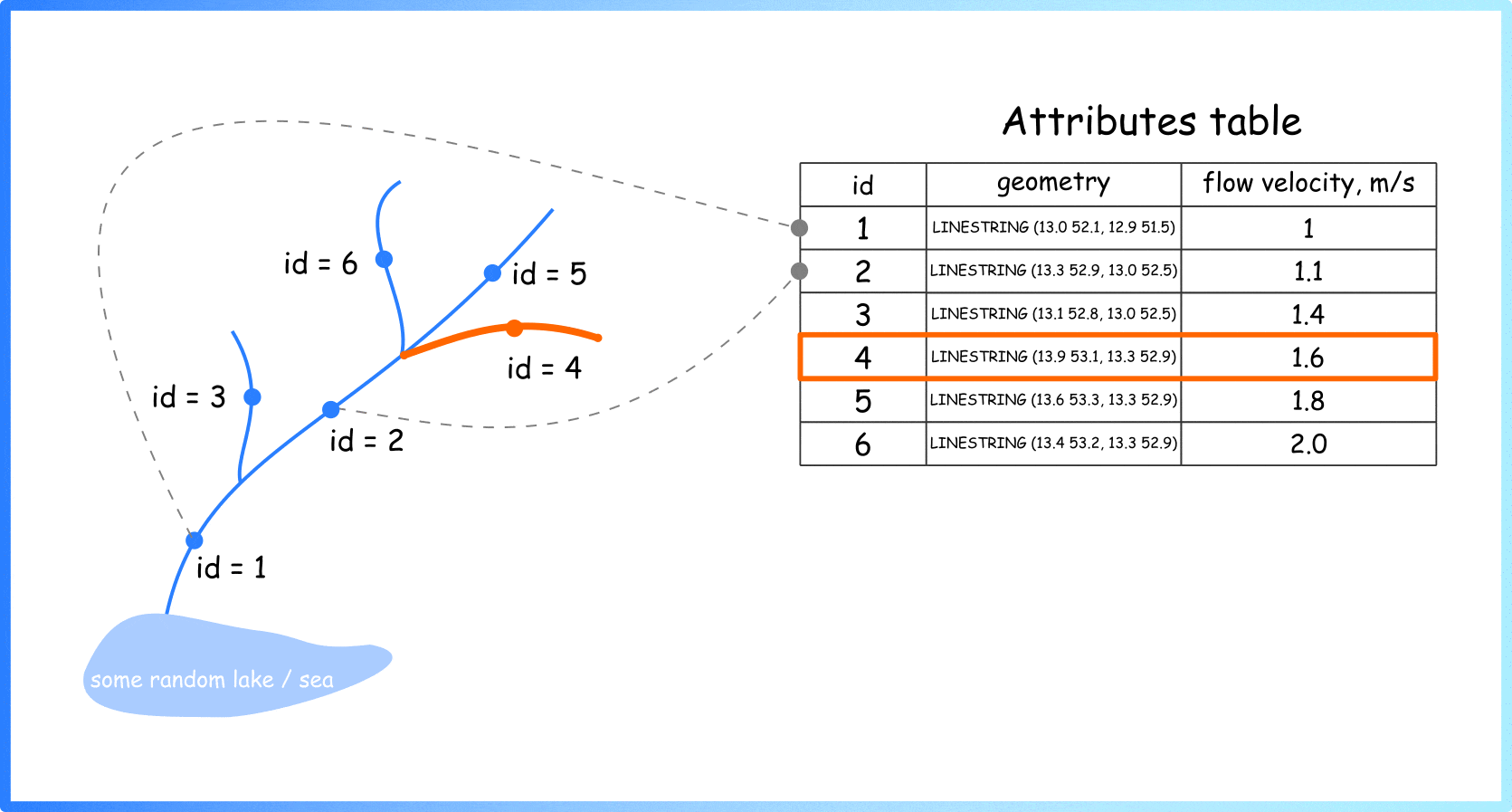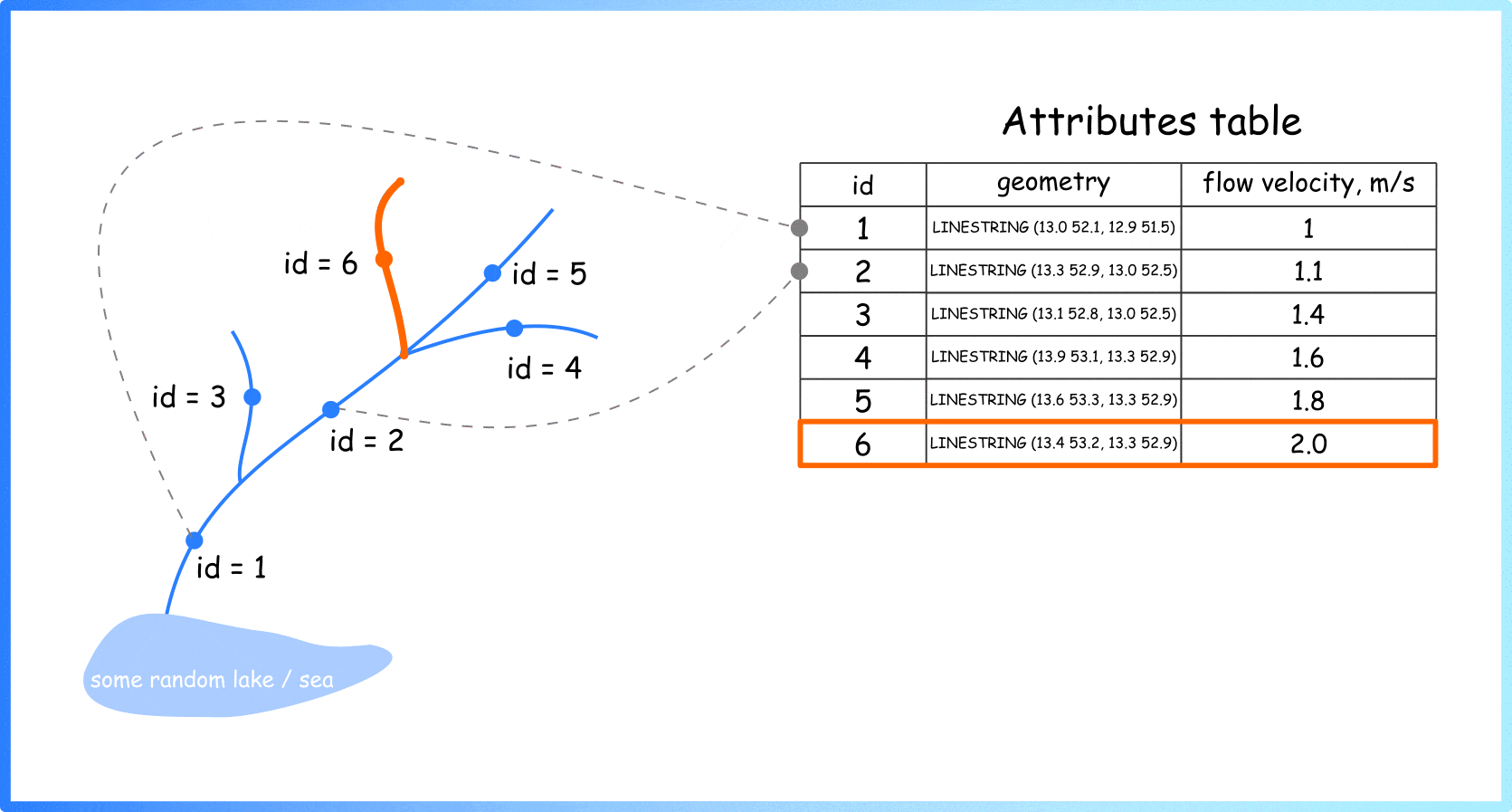
The constantly changing nature of the world around us poses a significant challenge for the development of AI models. Often, models are trained on longitudinal data with the hope that the training data used will accurately represent inputs the model may receive in the future. More generally, the default assumption that all training data are equally relevant often breaks in practice. For example, the figure below shows images from the CLEAR nonstationary learning benchmark, and it illustrates how visual features of objects evolve significantly over a 10 year span (a phenomenon we refer to as slow concept drift), posing a challenge for object categorization models.

Sample images from the CLEAR benchmark. (Adapted from Lin et al.)

Alternative approaches, such as online and continual learning, repeatedly update a model with small amounts of recent data in order to keep it current. This implicitly prioritizes recent data, as the learnings from past data are gradually erased by subsequent updates. However in the real world, different kinds of information lose relevance at different rates, so there are two key issues: 1) By design they focus exclusively on the most recent data and lose any signal from older data that is erased. 2) Contributions from data instances decay uniformly over time irrespective of the contents of the data.

In our recent work, “Instance-Conditional Timescales of Decay for Non-Stationary Learning”, we propose to assign each instance an importance score during training in order to maximize model performance on future data. To accomplish this, we employ an auxiliary model that produces these scores using the training instance as well as its age. This model is jointly learned with the primary model. We address both the above challenges and achieve significant gains over other robust learning methods on a range of benchmark datasets for nonstationary learning. For instance, on a recent large-scale benchmark for nonstationary learning (~39M photos over a 10 year period), we show up to 15% relative accuracy gains through learned reweighting of training data.

The challenge of concept drift for supervised learning

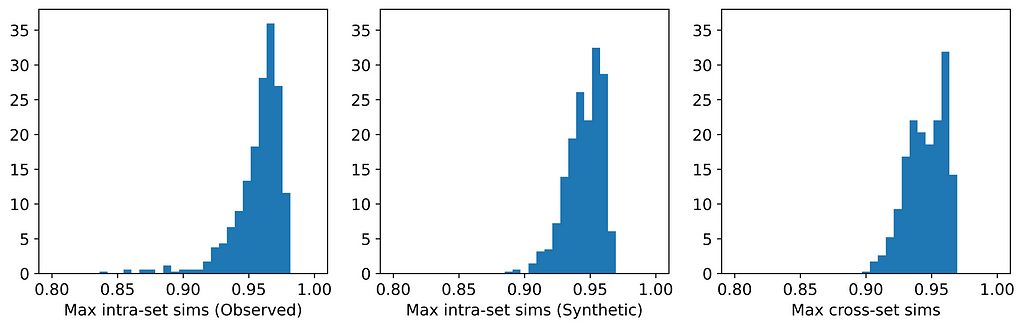
To gain quantitative insight into slow concept drift, we built classifiers on a recent photo categorization task, comprising roughly 39M photographs sourced from social media websites over a 10 year period. We compared offline training, which iterated over all the training data multiple times in random order, and continual training, which iterated multiple times over each month of data in sequential (temporal) order. We measured model accuracy both during the training period and during a subsequent period where both models were frozen, i.e., not updated further on new data (shown below). At the end of the training period (left panel, x-axis = 0), both approaches have seen the same amount of data, but show a large performance gap. This is due to catastrophic forgetting, a problem in continual learning where a model’s knowledge of data from early on in the training sequence is diminished in an uncontrolled manner. On the other hand, forgetting has its advantages — over the test period (shown on the right), the continual trained model degrades much less rapidly than the offline model because it is less dependent on older data. The decay of both models’ accuracy in the test period is confirmation that the data is indeed evolving over time, and both models become increasingly less relevant.

Comparing offline and continually trained models on the photo classification task.

Time-sensitive reweighting of training data

We design a method combining the benefits of offline learning (the flexibility of effectively reusing all available data) and continual learning (the ability to downplay older data) to address slow concept drift. We build upon offline learning, then add careful control over the influence of past data and an optimization objective, both designed to reduce model decay in the future.

Suppose we wish to train a model, M, given some training data collected over time. We propose to also train a helper model that assigns a weight to each point based on its contents and age. This weight scales the contribution from that data point in the training objective for M. The objective of the weights is to improve the performance of M on future data.

In our work, we describe how the helper model can be meta-learned, i.e., learned alongside M in a manner that helps the learning of the model M itself. A key design choice of the helper model is that we separated out instance- and age-related contributions in a factored manner. Specifically, we set the weight by combining contributions from multiple different fixed timescales of decay, and learn an approximate “assignment” of a given instance to its most suited timescales. We find in our experiments that this form of the helper model outperforms many other alternatives we considered, ranging from unconstrained joint functions to a single timescale of decay (exponential or linear), due to its combination of simplicity and expressivity. Full details may be found in the paper.

Instance weight scoring

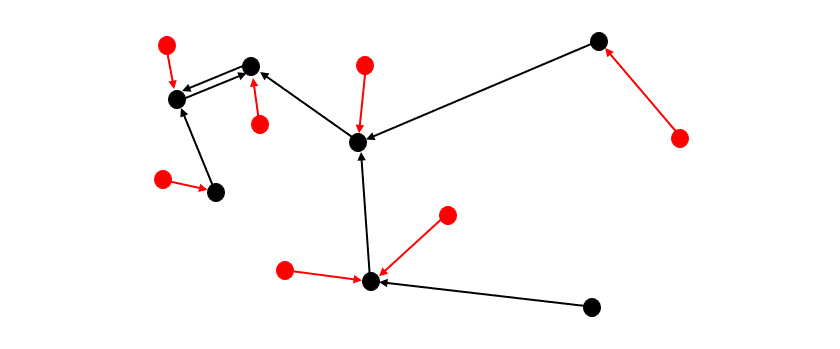
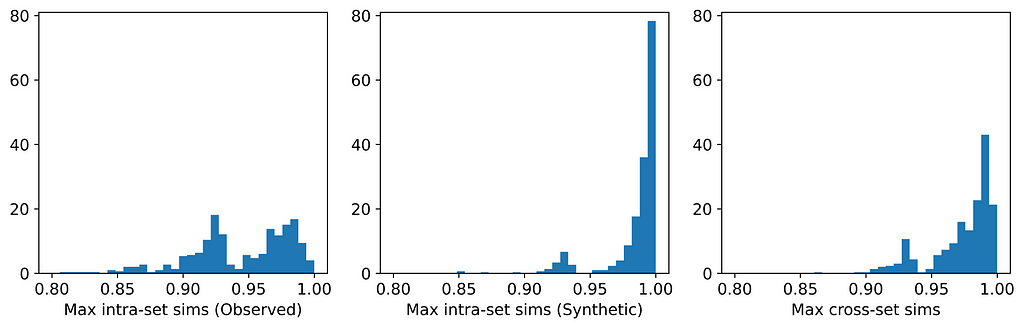
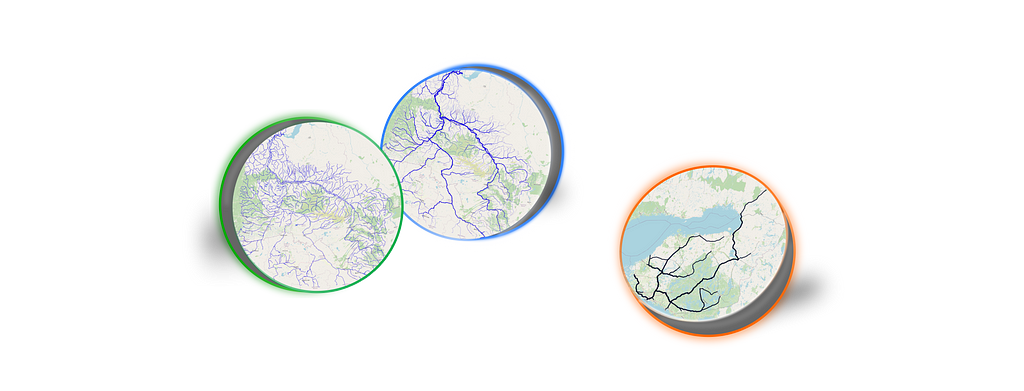
The top figure below shows that our learned helper model indeed up-weights more modern-looking objects in the CLEAR object recognition challenge; older-looking objects are correspondingly down-weighted. On closer examination (bottom figure below, gradient-based feature importance assessment), we see that the helper model focuses on the primary object within the image, as opposed to, e.g., background features that may spuriously be correlated with instance age.

Sample images from the CLEAR benchmark (camera & computer categories) assigned the highest and lowest weights respectively by our helper model.

Feature importance analysis of our helper model on sample images from the CLEAR benchmark.

Results

Gains on large-scale data

We first study the large-scale photo categorization task (PCAT) on the YFCC100M dataset discussed earlier, using the first five years of data for training and the next five years as test data. Our method (shown in red below) improves substantially over the no-reweighting baseline (black) as well as many other robust learning techniques. Interestingly, our method deliberately trades off accuracy on the distant past (training data unlikely to reoccur in the future) in exchange for marked improvements in the test period. Also, as desired, our method degrades less than other baselines in the test period.

Comparison of our method and relevant baselines on the PCAT dataset.

Broad applicability

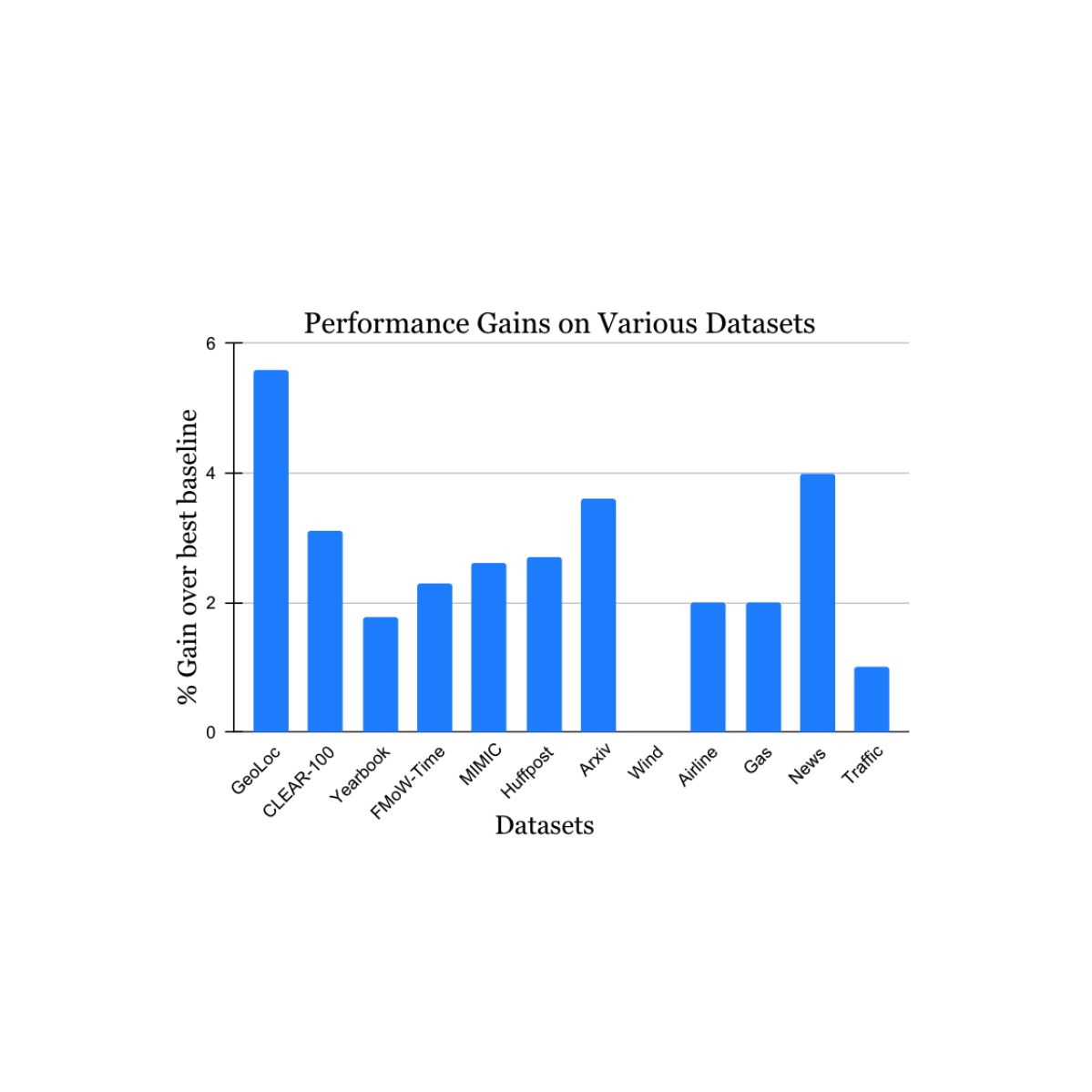
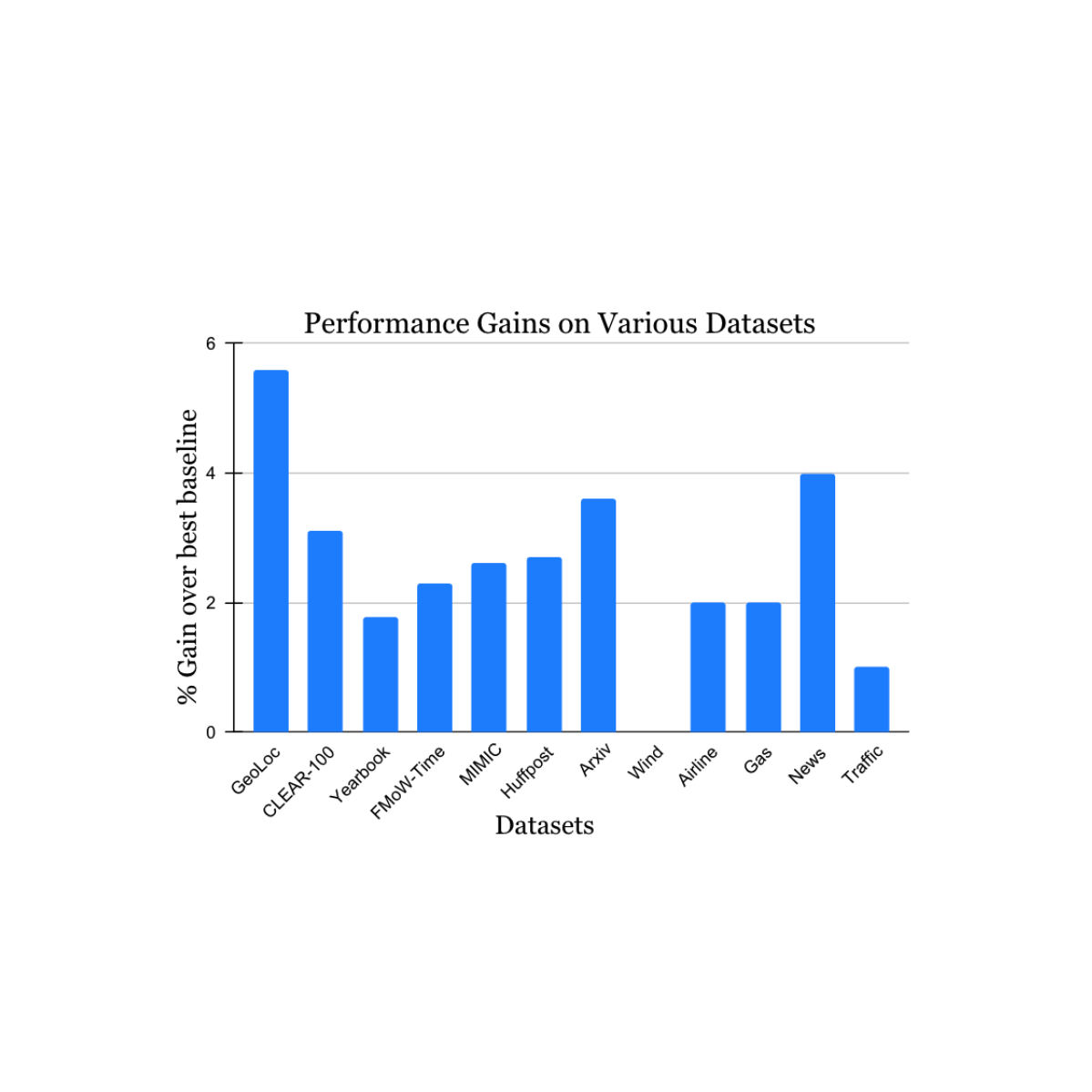
We validated our findings on a wide range of nonstationary learning challenge datasets sourced from the academic literature (see 1, 2, 3, 4 for details) that spans data sources and modalities (photos, satellite images, social media text, medical records, sensor readings, tabular data) and sizes (ranging from 10k to 39M instances). We report significant gains in the test period when compared to the nearest published benchmark method for each dataset (shown below). Note that the previous best-known method may be different for each dataset. These results showcase the broad applicability of our approach.

Performance gain of our method on a variety of tasks studying natural concept drift. Our reported gains are over the previous best-known method for each dataset.

Extensions to continual learning

Finally, we consider an interesting extension of our work. The work above described how offline learning can be extended to handle concept drift using ideas inspired by continual learning. However, sometimes offline learning is infeasible — for example, if the amount of training data available is too large to maintain or process. We adapted our approach to continual learning in a straightforward manner by applying temporal reweighting within the context of each bucket of data being used to sequentially update the model. This proposal still retains some limitations of continual learning, e.g., model updates are performed only on most-recent data, and all optimization decisions (including our reweighting) are only made over that data. Nevertheless, our approach consistently beats regular continual learning as well as a wide range of other continual learning algorithms on the photo categorization benchmark (see below). Since our approach is complementary to the ideas in many baselines compared here, we anticipate even larger gains when combined with them.

Results of our method adapted to continual learning, compared to the latest baselines.

Conclusion

We addressed the challenge of data drift in learning by combining the strengths of previous approaches — offline learning with its effective reuse of data, and continual learning with its emphasis on more recent data. We hope that our work helps improve model robustness to concept drift in practice, and generates increased interest and new ideas in addressing the ubiquitous problem of slow concept drift.

Acknowledgements

We thank Mike Mozer for many interesting discussions in the early phase of this work, as well as very helpful advice and feedback during its development.

Effective self-service options are becoming increasingly critical for contact centers, but implementing them well presents unique challenges. Amazon Lex provides your Amazon Connect contact center with chatbot functionalities such as automatic speech recognition (ASR) and natural language understanding (NLU) capabilities through voice and text channels. The bot takes natural language speech or text input, recognizes […]

Pose estimation is a computer vision technique that detects a set of points on objects (such as people or vehicles) within images or videos. Pose estimation has real-world applications in sports, robotics, security, augmented reality, media and entertainment, medical applications, and more. Pose estimation models are trained on images or videos that are annotated with […]

With the advent of generative AI solutions, organizations are finding different ways to apply these technologies to gain edge over their competitors. Intelligent applications, powered by advanced foundation models (FMs) trained on huge datasets, can now understand natural language, interpret meaning and intent, and generate contextually relevant and human-like responses. This is fueling innovation across […]

Stream Ordering: How And Why a Geo-Scientist Sometimes Needed to Rank Rivers on a Map

Learn how to obtain Strahler or Shreve order on vector layer

Dear reader, in this article, I would like to dive into one exciting hydrological topic. I will start with the picture:

Disclaimer: this article is written both for geographers who face the problem of ranking river vector layer using geoinformation systems (GIS) and for people who have sometimes seen “nice rivers” on a map but do not know exactly how they are made. We will together sequentially explore how spatial data are represented in GIS applications, the way the structure of river networks can be analysed, and what visualisation techniques can be used.

Now the question is: Which map looks prettier? — For me, the one on the bottom (b).

Actually, the second visualisation is more correct from a common sense point of view as well. The more tributaries flowing into the riverbed, the wider and fuller the river will be. For example, one of the largest rivers in the world, the Nile, at its source (high in the mountains), barely resembles a powerful river at its mouth: with each kilometer of the way to the sea, the river absorbs more and more tributaries and becomes more and more full-flowing.

The map shown above (Figure 1b) was prepared on the basis of structural information on the river network. In this post I would like to discuss in which ways this additional information about rivers can be obtained and what tools can be used for this purpose.

What is the river

Let’s start by explaining how information about rivers is represented. In cartography and geo-sciences, rivers are represented as a linear vector layer: each river section is represented as a line with some characteristics. For example, the length of the section, its geographic coordinates (geometry of the object), ground type, average depth, flow velocity, etc. (Animation 1).

So, generally, if you see a river on a map, you see a set of these simple geometric primitives (individual rows in attrbute table) assembled into one big system. Different colours can be used to visualise stored characteristics (Figure 2).

Either programming languages or specialised applications such as ArcGIS (proprietary software) or QGIS (open-source) are used for visualisation.

River structure

Such information in the attributes table on rivers can be collected in different ways: from remote sensing data, expeditions, gauges, and hydrological stations. However, information about the river structure is usually assigned by the specialist at the very last moment, when he or she sees on the map what the whole system looks like. For example, a researcher can themselves add a new column to the vector layer description in which they assign a rank to each river segment (Figure 3).

Now we can see that the picture resembles the map from the beginning of the article (Figure 1b). But the question arises: what principle can be used to assign such values? — the answer is: a lot. There are several generally accepted systems for ranking watercourses in hydrology — see the Stream order wiki page or paper Stream orders. Below are a few approaches that I have used myself during the work (Figure 4).

For what reason

Now it is time to answer the question of the purpose of such ranking systems. We can distinguish two reasons:

• Visualisation — using rank as an attribute of the size of a linear object on the map, it is possible to create nice maps (Figure 1);
• Further analysis.

Knowledge of river network structure can be combined with other characteristics for further analysis, e.g. to identify the following patterns (Figure 5).

How to assign stream orders using existing tools

It is difficult to rank large systems manually, so specialised tools have been created for stream ordering. There are two fundamentally different ways:

• Stream ordering using raster data (digital elevation model);
• Stream ordering on vector layers.

Above, we have described how we can assign ranks to vector layers. However, spatial data are often represented in another format — as rasters (matrices) (Figure 6). Digital elevation models (matrices where each pixel has a specific size, such as 90 by 90 metres, for example, and an elevation value above the sea level surface that is stored in each cell of that matrix) are particularly commonly used.

The raster layer (digital elevation model — DEM) is used to calculate the flow direction matrix and flow accumulation. The Stream Order (Spatial Analyst) tool in ArcGIS, for example, works according to this principle. In this post I will not describe in detail how such an algorithm works, as there are quite nice visualisations and descriptions in the official documentation (please check Flow Direction function page if you want to know more). Below I have listed some of the tools you can use to get an Strahler order using raster data:

• ArcGIS: Stream Order from a Digital Elevation Model (DEM) using ArcGIS;
• QGIS: Calculate Strahler Stream Orders in QGIS;
• GRASS: r.stream.order tool.

However, this all requires a lot of raster data manipulation. What should you do if you already have a vector layer? (This can happen if you have, for example, a vector layer of the river network loaded from OpenStreetMap.) I’ll tell you next!

How to obtain Shreve, Strahler and Topological order on vector layer using QGIS

During our work four years ago, my colleagues and I came up with an algorithm that allows us to calculate Shreve, Strahler, and Topological order based only on the vector layer and the final point (the point where the river system ends and flows into a lake / sea / ocean). The first version of the algorithm is described in my first article on medium: “The Algorithm for Ranking the Segments of the River Network for Geographic Information Analysis Based on Graphs” (wiping away a tear of nostalgia). Recently, I finally got around to writing some clearer documentation for it and preparing a plugin update.

In QGIS for stream ordering, the Lines Ranking plugin can be used. To use, it will require loading a vector layer, reprojecting it into the desired metric projection, and assigning a final point (you can just click on the map) — the following result will be obtained (Figure 7).

Now you, dear reader, have dived a little deeper into the topic of stream ordering in hydrology and learned how to use different tools to get it from raw data (raster or vector). Once there is information about the river’s structure, you can prepare beautiful and clear visualisations, or continue the analysis by combining the obtained information with other characteristics.

Useful links:

• Lines ranking plugin documentation: https://linesranking.readthedocs.io/en/latest
• Repository with source code of the plugin: https://github.com/ChrisLisbon/QGIS_LinesRankingPlugin

The talk on stream ordering in hydrology was presented by Mikhail Sarafanov

---

Stream Ordering: How And Why a Geo-scientist Sometimes Needed to Rank Rivers on a Map was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Architecture patterns and mental models for working with Large Language Models

The Need For AI Patterns

We all anchor to some tried and tested methods, approaches and patterns when building something new. This statement is very true for those in software engineering, however for generative AI and artificial intelligence itself this may not be the case. With emerging technologies such as generative AI we lack well documented patterns to ground our solution’s.

Here I share a handful of approaches and patterns for generative AI, based on my evaluation of countless production implementations of LLM’s in production. The goal of these patterns is to help mitigate and overcome some of the challenges with generative AI implementations such as cost, latency and hallucinations.

List of Patterns

1. Layered Caching Strategy Leading To Fine-Tuning
2. Multiplexing AI Agents For A Panel Of Experts
3. Fine-Tuning LLM’s For Multiple Tasks
4. Blending Rules Based & Generative
5. Utilizing Knowledge Graphs with LLM’s
6. Swarm Of Generative AI Agents
7. Modular Monolith LLM Approach With Composability
8. Approach To Memory Cognition For LLM’s
9. Red & Blue Team Dual-Model Evaluation

1) Layered Caching Strategy Leading To Fine-Tuning

Here we are solving for a combination of factors from cost, redundancy and training data when introducing a caching strategy and service to our large language models.

By caching these initial results, the system can serve up answers more rapidly on subsequent queries, enhancing efficiency. The twist comes with the fine-tuning layer once we have sufficient data, where feedback from these early interactions is used to refine a more specialized model.

The specialized model not only streamlines the process but also tailors the AI’s expertise to specific tasks, making it highly effective in environments where precision and adaptability are paramount, like customer service or personalized content creation.

For getting started there are pre-built services such as GPTCache or roll your own with common caching databases such as Redis, Apache Cassandra, Memcached. Be sure you monitor and measure your latency as you add additional services to the mix.

2) Multiplexing AI Agents For A Panel Of Experts

Imagine an ecosystem where multiple generative AI models orientated to a specific task (“agents”), each a specialist within its domain, work in parallel to address a query. This multiplexing strategy enables a diverse set of responses, which are then integrated to provide a comprehensive answer.

This setup is ideal for complex problem-solving scenarios where different aspects of a problem require different expertise, much like a team of experts each tackling a facet of a larger issue.

A larger model such as a GPT-4 is used to understand context and break this down into specific tasks or information requests which are passed to smaller agents. Agents could be smaller language models such as Phi-2 or TinyLlama that have been trained on specific tasks, access to specific tools or generalized models such as GPT, Llama with specific personality, context prompts and function calls.

3) Fine-Tuning LLM’s For Multiple Tasks

Here we fine-tune a large language model on multiple tasks simultaneously instead of a single task. It’s an approach that promotes a robust transfer of knowledge and skills across different domains, enhancing the model’s versatility.

This multi-task learning is especially useful for platforms that need to handle a variety of tasks with a high degree of competence, such as virtual assistants or AI-powered research tools. This could potentially simplify workflows for training and testing for a complex domain.

Some resources and packages for training LLM’s include DeepSpeed, and the training functions on Hugging Face’s Transformer library.

4) Blending Rules Based & Generative

A number of existing business systems and organizational applications are still somewhat rules based. By fusing the generative with the structured precision of rule-based logic, this pattern aims to produce solutions that is both creative yet compliant.

It’s a powerful strategy for industries where outputs must adhere to stringent standards or regulations, ensuring the AI remains within the bounds of desired parameters while still being able to innovate and engage. A good example of this is generating intents and message flows for a phone call IVR system or traditional (non-llm based) chat bots which is rules based.

5) Utilizing Knowledge Graphs with LLM’s

Integrating knowledge graphs with generative AI models gives them a fact orientated super power, allowing for outputs that are not only contextually aware but also more factually correct.

This approach is crucial for applications where truth and accuracy are non-negotiable, such as in educational content creation, medical advice, or any field where misinformation could have serious consequences.

Knowledge graphs and graph ontologies (set of concepts for a graph) allow for complex topics or organizational problems to be broken into a structured format to help ground a large language model with deep context. You can also use a language model to generate the ontologies in a format such as JSON or RDF, example prompt I created you can use.

Services you can use for knowledge graphs include graph database services such as ArangoDB, Amazon Neptune, Azure Cosmos DB and Neo4j. There are also wider datasets and services for accessing broader knowledge graphs including Google Enterprise Knowledge Graph API, PyKEEN Datasets, and Wikidata.

6) Swarm Of AI Agents

Drawing inspiration from natural swarms and heards, this model employs a multitude of AI agents that collectively tackle a problem, each contributing a unique perspective.

The resulting aggregated output reflects a form of collective intelligence, surpassing what any individual agent could achieve. This pattern is particularly advantageous in scenarios that require a breadth of creative solutions or when navigating complex datasets.

An example of this could be reviewing a research paper from a multiple “experts” point of view, or assessing customer interactions for many use-cases at once from fraud to offers. We take these collective “agents” and combine all their inputs together. For high volume swarm’s you can look at deploying messaging services such as Apache Kafka to handle the messages between the agents and services.

7) Modular Monolith LLM Approach With Composability

This design champions adaptability, featuring a modular AI system that can dynamically reconfigure itself for optimal task performance. It’s akin to having a Swiss Army knife, where each module can be selected and activated as needed, making it highly effective for businesses that require tailor-made solutions for varying customer interactions or product needs.

You can deploy the use of various autonomous agent frameworks and architectures to develop each of your agents and their tools. Example frameworks include CrewAI, Langchain, Microsoft Autogen and SuperAGI.

For a sales modular monolith this could be agents focused on prospecting, one handling bookings, one focused on generating messaging, and another updating databases. In future as specific services become available from specialized AI companies, you can swap out a module for an external or 3rd party service for a given set of tasks or domain specific problems.

8) Approach To Memory Cognition For LLM’s

This approach introduces an element of human-like memory to AI, allowing models to recall and build upon previous interactions for more nuanced responses.

It’s particularly useful for ongoing conversations or learning scenarios, as the AI develops a more profound understanding over time, much like a dedicated personal assistant or an adaptive learning platform. Memory cognition approaches can be developed through summation and storing key events and discussions into a vector database over time.

To keep compute of summaries low, you can leverage summation through smaller NLP libraries such as spaCy, or BART language models if dealing with considerable volumes. Databases used are vector based and retrieval during prompt stage to check the short-term memory uses a similarity search to locate key “facts”. For those interested on a working solution there is an open-sourced solution following a similar pattern called MemGPT.

9) Red & Blue Team Dual-Model Evaluation

In the Red and Blue team evaluation model, one AI generates content while another critically evaluates it, akin to a rigorous peer-review process. This dual-model setup is excellent for quality control, making it highly applicable in content generation platforms where credibility and accuracy are vital, such as news aggregation or educational material production.

This approach can be used to replace parts of human feedback for complex tasks with a fine-tuned model to mimic the human review process and refine the results for evaluating complex language scenarios and outputs.

Takeaways

These design patterns for generative AI are more than mere templates; but the frameworks upon which the intelligent systems of tomorrow will grow. As we continue to explore and innovate, it’s clear that the architecture we choose will define not just the capabilities but the very identity of the AI we create.

By no means this list is final, we will see this space develop as the patterns and use cases for generative AI expands. This write-up was inspired by the AI design patterns published by Tomasz Tunguz.

Enjoyed This Story?

Vincent Koc is a highly accomplished, commercially-focused technologist and futurist with a wealth of experience focused in data-driven and digital disciplines.

Subscribe for free to get notified when Vincent publishes a new story. Or follow him on LinkedIn and X.

Get an email whenever Vincent Koc publishes.

Unless otherwise noted, all images are by the author

---

Generative AI Design Patterns: A Comprehensive Guide was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.