Learn how you can incorporate multimodal information into your machine-learning system
Originally appeared here:
How to Create Powerful AI Representations by Combining Multimodal Information
Learn how you can incorporate multimodal information into your machine-learning system
Originally appeared here:
How to Create Powerful AI Representations by Combining Multimodal Information



There are, in essence, two ways to prove the Central Limit Theorem. The first one is empirical while the second one employs the quietly perfect precision of mathematical thought. I’ll cover both methods in this article.
In the empirical method, you will literally see the Central Limit Theorem working, or sort of working, or completely failing to work in the snow-globe universe created by your experiment. The empirical method doesn’t so much prove the CLT as test its validity on the given data. I’ll perform this experiment, but not on synthetically simulated data. I’ll use actual, physical objects — the sorts that you can pick up with your fingers, hold them in front of your eyes, and pop them in your mouth. And we’ll test the outcome of this experiment for normality.
The theoretical method is a full-fledged mathematical proof of the CLT that weaves through a stack of five concepts:
Supporting this ponderous edifice of concepts is the vast and verdant field of infinitesimal calculus (or simply, ‘calculus’).
I’ll explain each of the five concepts and show how each one builds upon the one below it until they all unite to prove what is arguably one of the most far-reaching and delightful theorems in statistical science.
In a nutshell, the CLT makes the following power-packed assertion:
The standardized sample mean converges in distribution to the standard normal random variable.
Four terms form the fabric of this definition:
standardized, meaning a random variable from which you’ve subtracted its mean thereby sliding the entire sample along the X-axis to the point where it’s mean is zero, then divided this translated sample by its standard deviation thereby expressing the value of each data point purely in terms of the fractional number of standard deviations from the mean.
sample mean, which is simply the mean of your random sample.
converges in distribution, which means that as your sample swells to an infinitely large size, the Cumulative Probability Function (CDF) of a random variable that you have defined on the sample (in our case, it is the sample mean) looks more and more like the CDF of some other random variable of interest (in our case, the other variable is the standard normal random variable). And that brings us to,
the standard normal random variable which is a random variable with zero mean and a unit variance, and which is normally distributed.
If you are willing to be forgiving of accuracy, here’s a colloquial way of stating the Central Limit Theorem that doesn’t grate as harshly on the senses as the formal definition:
For large sample sizes, sample means are more or less normally distributed around the true, population mean.
And now, we weigh some candy.
They say a lawyer’s instinct is to sue, an artist’s instinct is to create, a surgeon’s, to cut you open and see what’s inside. My instinct is to measure. So I bought two packs of Nerds with the aim of measuring the mean weight of a Nerd.

But literally tens of millions of Nerds have been produced to pander to the candy cravings of people like me. Thousands more will be produced by the time you reach the end of this sentence. The population of Nerds was clearly inaccessible to me, and so was the mean weight of the population. My goal to know the mean weight of a Nerd was in danger of being still born.
What Nature won’t readily reveal, one must infer. So I combined the contents of the two boxes, selected 30 Nerds at random (15 each of grape and strawberry), weighed this sample, computed its mean, and returned the sample to the pile.

I repeated this process 50 times and got 50 different sample means:

Some of you might recognize what I did. I was bootstrapping of course.
Next, I standardized each of the 50 sample means using the following formula:

Here, 0.039167 was the mean of the 50 sample means, and 0.006355 was their standard deviation.
A frequency distribution plot of the 50 standardized means revealed the following distributional shape:

The sample means appeared to be arranged neatly around the unknown (and never to be known) population mean in what looked like a normal distribution. But was the distribution really normal? How could I be sure that it wouldn’t turn into the following shape for larger sample sizes or a greater number of samples?

In the early 1800s, when Pierre-Simon Laplace was developing his ideas on what came to be known as the Central Limit Theorem, he evaluated many such distributional shapes. In fact, the one shown above was one of his favorites. Another close contender was the normal curve discovered by his fellow countryman Abraham De Moivre. You see, in those days, the normal distribution wasn’t called by its present name. And neither was its wide-ranging applicability discovered. At any rate, it definitely wasn’t regarded with the exalted level of reverence it enjoys today.
To know whether my data was indeed normally distributed, what I needed was a statistical test of normality — a test that would check whether my data obeyed the distributional properties of the normal curve. A test that would assure me that I could be X% sure that the distribution of my sample means wouldn’t crushingly morph into anything other than the normal curve were I to increase the sample size or draw a greater number of samples.
Thankfully, my need was not only a commonly felt one, but also a heavily researched one. So heavily researched is this area that during the past 100 years, scientists have invented no less than ten different tests of normality with publications still gushing out in large volume. One such test was invented in 1980 by Messieurs Carlos Jarque and Anil K. Bera. It’s based on a disarmingly simple observation. If your data were normally distributed, then its skewness (S) would be zero and kurtosis (K) would be 3 (I’ll explain what those are later in this article). Using S, K, and the sample size n, Mssrs. Jarque and Bera constructed a special random variable called JB as follows:

JB is the test statistic. The researchers proved that JB will be Chi-squared distributed with 2 degrees of freedom provided your data comes from a normally distributed population. The null hypothesis of this test is that your data is normally distributed. And the p-value of the test statistic is the probability of your data coming from a normally distributed population. Their test came to be known as the Jarque-Bera test of normality. You can also read all the JB-test in this article.
When I ran the JB-test on the set of 50 sample means, the test came back to say that I would be less than wise to reject the test’s null hypothesis. The test statistic was jb(50) = 0.30569, p = .86.
Here’s a summary of the empirical method I conducted:
It is common knowledge that careful scientific experimentation is an arduous and fuel-intensive endeavor, and my experiment was no exception. Hence, after my experiment was completed I helped myself to a generous serving of candy. All in the name of science obviously.
There are two equally nice ways to mathematically prove the CLT, and this time I really mean prove. The first one uses the properties of Characteristic Functions. The second one uses the properties of Moment Generating Functions (MGF). The CF and the MGF are different forms of generating functions (more on that soon). The CF-based proof makes fewer assumptions than the MGF-based proof. It’s also generally speaking a solid, self-standing proof. But I won’t use it because I like MGFs more than I like CFs. So we’ll follow the line of thought adopted by Casella and Berger (see references) which uses the MGF-based approach.
Lest you are still itching to know what the CF-based proof looks like, Wikipedia has a 5-line proof of the CLT that uses Characteristic Functions, presented in the characteristically no-nonsense style of that platform. I am sure it will be a joy to go through.
Returning to the MGF-based proof, you’ll be able to appreciate it to the maximum if you know the following four concepts:
I’ll begin by explaining these concepts. If you know what they are already, you can go straight to the proof, and I’ll see you there.
A sequence is just an arrangement of stuff in some order. The figure on the left is a “bag” or a “set” (strictly speaking, a “multiset”) of Nerds. If you line up the contents of this bag, you get a sequence.

In a sequence, order matters a lot. In fact, order is everything. Remove the ordering of the elements, and they fall back to being just a bag.
In math, a sequence of (n+1) elements is written as follows:

Here are some examples of sequences and their properties:

The last sequence, although containing an infinite number of terms, converges to 1, as k marches through the set of natural numbers: 1, 2, 3,…∞.
Sequences have many other fascinating properties which will be of no interest to us.
Take any sequence. Now replace the comma between its elements with a plus sign. What you got yourself is a Series:

A series is finite or infinite depending on the number of terms in it. Either way, if it sums to a finite value, it’s a convergent series. Else it’s a divergent series.
Here are some examples.

In the second series, x is assumed to be finite.
Instead of adding all elements of a sequence, if you multiply them, what you get is a product series. Perhaps the most famous example of an infinite convergent product series is the following one:

A historical footnote is in order. We assign credit for not only the above formula for ‘e’ but also to the discovery of value of ‘e’ to the 17th century Swiss mathematician Jacob Bernoulli (1655–1705), although he didn’t call it ‘e’. The name ‘e’ was reportedly given by another Swiss math genius — the great Leonhard Euler (1707–1783). If that report is true, then poor Bernoulli missed his chance to name his creation (‘b’ ?).

During the 1690s, Bernoulli also discovered the Weak Law of Large Numbers. And with that landmark discovery, he also set in motion a train of thought on limit theorems and statistical inference that kept rolling well into the 20th century. Along the way came an important discovery, namely Pierre-Simon Laplace’s discovery of the Central Limit Theorem in 1810. In what must be one of the best tributes to Jacob Bernoulli, the final step in the (modern) proof of the Central Limit Theorem, the step that links the entire chain of derivations lying before it with the final revelation of normality, relies upon the very formula for ‘e’ that Bernoulli discovered in the late 1600s.
Let’s return to our parade of topics. An infinite series forms the basis for generating functions which is the topic I will cover next.
The trick to understanding Generating Function is to appreciate the usefulness of a…Label Maker.

Imagine that your job is to label all the shelves of newly constructed libraries, warehouses, storerooms, pretty much anything that requires an extensive application of labels. Anytime they build a new warehouse in Boogersville or revamp a library in Belchertown (I am not entirely making these names up), you get a call to label its shelves.

So imagine then that you just got a call to label out a shiny new warehouse. The aisles in the warehouse go from 1 through 26, and each aisle runs 50 spots deep and 5 shelves tall.
You could just print out 6500 labels like so:
A.1.1, A.1.2,…,A.1.5, A.2.1,…A.2.5,…,A50.1,…,A50.5,
B1.1,…B2.1,…,B50.5,.. and so on until Z.50.5,
And you could present yourself along with your suitcase stuffed with 6500 florescent dye coated labels at your local airport for a flight to Boogersville. It might take you a while to get through airport security.
Or here’s an idea. Why not program the sequence into your label maker? Just carry the label maker with you. At Boogersville, load the machine with a roll of tape, and off you go to the warehouse. At the warehouse, you press a button on the machine, and out flows the entire sequence for aisle ‘A’.
Your label maker is the generating function for this, and other sequences like this one:
A.1.1, A.1.2,…,A.1.5, A.2.1,…A.2.5,…,A50.1,…,A50.5
In math, a generating function is a mathematical function that you design for generating sequences of your choosing so that you don’t have to remember the entire sequence.
If your proof uses a sequence of some kind, it’s often easier to substitute the sequence with its generating function. That instantly saves you the trouble of lugging around the entire sequence across your proof. Any operations, like differentiation, that you planned to perform on the sequence, you can instead perform them on its generating function.
But wait there’s more. All of the above advantages are magnified whenever the generating sequence has a closed form like the formula for e to the power x that we saw earlier.
A really simple generating function is the one shown in the figure below for the following infinite sequence: 1,1,1,1,1,…:

As you can see, a generating sequence is actually a series.
A slightly more complex generating sequence, and a famous one, is the one that generates a sequence of (n+1) binomial coefficients:

Each coefficient nCk gives you the number of different ways of choosing k out of n objects. The generating function for this sequence is the binomial expansion of (1 + x) to the power n:

In both examples, it’s the coefficients of the x terms that constitute the sequence. The x terms raised to different powers are there primarily to keep the coefficients apart from each other. Without the x terms, the summation will just fuse all the coefficients into a single number.
The two examples of generating functions I showed you illustrate applications of the modestly named Ordinary Generating Function. The OGF has the following general form:

Another greatly useful form is the Exponential Generating Function (EGF):

It’s called exponential because the value of the factorial term in the denominator increases at an exponential rate causing the values of the successive terms to diminish at an exponential rate.
The EGF has a remarkably useful property: its k-th derivative, when evaluated at x=0 isolates out the k-th element of the sequence a_k. See below for how the 3rd derivative of the above mentioned EGF when evaluated at x=0 gives you the coefficient a_3. All other terms disappear into nothingness:

Our next topic, the Taylor series, makes use of the EGF.
The Taylor series is a way to approximate a function using an infinite series. The Taylor series for the function f(x) goes like this:

In evaluating the first two terms, we use the fact that 0! = 1! = 1.
f⁰(a), f¹(a), f²(a), etc. are the 0-th, 1st, 2nd, etc. derivatives of f(x) evaluated at x=a. f⁰(a) is simple f(a). The value ‘a’ can be anything as long as the function is infinitely differentiable at x = a, that is, it’s k-th derivative exists at x = a for all k from 1 through infinity.
In spite of its startling originality, the Taylor series doesn’t always work well. It creates poor quality approximations for functions such as 1/x or 1/(1-x) which march off to infinity at certain points in their domain such as at x = 0, and x = 1 respectively. These are functions with singularities in them. The Taylor series also has a hard time keeping up with functions that fluctuate rapidly. And then there are functions whose Taylor series based expansions will converge at a pace that will make continental drifts seem recklessly fast.
But let’s not be too withering of the Taylor series’ imperfections. What is really astonishing about it is that such an approximation works at all!
The Taylor series happens be to one of the most studied, and most used mathematical artifacts.
On some occasions, the upcoming proof of the CLT being one such occasion, you’ll find it useful to split the Taylor series in two parts as follows:

Here, I’ve split the series around the index ‘r’. Let’s call the two pieces T_r(x) and R_r(x). We can express f(x) in terms of the two pieces as follows:

T_r(x) is known as the Taylor polynomial of order ‘r ’ evaluated at x=a.
R_r(x) is the remainder or residual from approximating f(x) using the Taylor polynomial of order ‘r’ evaluated at x=a.
By the way, did you notice a glint of similarity between the structure of the above equation, and the general form of a linear regression model consisting of the observed value y, the modeled value β_capX, and the residual e?

But let’s not dim our focus.
Returning to the topic at hand, Taylor’s theorem, which we’ll use to prove the Central Limit Theorem, is what gives the Taylor’s series its legitimacy. Taylor’s theorem says that as x → a, the remainder term R_r(x) converges to 0 faster than the polynomial (x — a) raised to the power r. Shaped into an equation, the statement of Taylor’s theorem looks like this:

One of the great many uses of the Taylor series lies in creating a generating function for the moments of random variable. Which is what we’ll do next.
The k-th moment of a random variable X is the expected value of X raised to the k-th power.

This is known as the k-th raw moment.
The k-th moment of X around some value c is known as the k-th central moment of X. It’s simply the k-th raw moment of (X — c):

The k-th standardized moment of X is the k-th central moment of X divided by k-th power of the standard deviation of X:

The first 5 moments of X have specific values or meanings attached to them as follows:
After the 4th moment, the interpretations become assuredly murky.
With so many moments flying around, wouldn’t it be terrific to have a generating function for them? That’s what the Moment Generating Function (MGF) is for. The Taylor series makes it super-easy to create the MGF. Let’s see how to create it.
We’ll define a new random variable tX where t is a real number. Here’s the Taylor series expansion of e to the power tX evaluated at t = 0:

Let’s apply the Expectation operator on both sides of the above equation:

By linearity (and scaling) rule of expectation: E(aX + bY) = aE(X) + bE(Y), we can move the Expectation operator inside the summation as follows:

Recall that E(X^k] are the raw moments of X for k = 0,1,23,…
Let’s compare Eq. (2) with the general form of an Exponential Generating Function:

What do we observe? We see that E(X^k] in Eq. (2) are the coefficients a_k in the EGF. Thus Eq. (2) is the generating function for the moments of X, and so the formula for the Moment Generating Function of X is the following:

The MGF has many interesting properties. We’ll use a few of them in our proof of the Central Limit Theorem.
Remember how the k-th derivative of the EGF when evaluated at x = 0 gives us the k-th coefficient of the underlying sequence? We’ll use this property of the EGF to pull out the moments of X from its MGF.
The zeroth derivative of the MGF of X evaluated at t = 0 is obtained by simply substituting t = 0 in Eq. (3). M⁰_X(t=0) evaluates to 1. The first, second, third, etc. derivatives of the MGF of X evaluated at t = 0 are denoted by M¹_X(t=0), M²_X(t=0), M³_X(t=0), etc. They evaluate respectively to the first, second, third etc. raw moments of X as shown below:

This gives us our first interesting and useful property of the MGF. The k-th derivative of the MGF evaluated at t = 0 is the k-th raw moment of X.

The second property of MGFs which we’ll find useful in our upcoming proof is the following: if two random variables X and Y have identical Moment Generating Functions, then X and Y have identical Cumulative Distribution Functions:

If X and Y have identical MGFs, it implies that their mean, variance, skewness, kurtosis, and all higher order moments (whatever humanly unfathomable aspects of reality those moments might represent) are all one-is-to-one identical. If every single property exhibited by the shapes of X and Y’s CDF is correspondingly the same, you’d expect their CDFs to also be identical.
The third property of MGFs we’ll use is the following one that applies to X when X scaled by ‘a’ and translated by ‘b’:

The fourth property of MGFs that we’ll use applies to the MGF of the sum of ‘n’ independent, identically distributed random variables:

A final result, before we prove the CLT, is the MGF of a standard normal random variable N(0, 1) which is the following (you may want to compute this as an exercise):

Speaking of the standard normal random variable, as shown in Eq. (4), the first, second, third, and fourth derivatives of the MGF of N(0, 1) when evaluated at t = 0 will give you the first moment (mean) as 0, the second moment (variance) as 1, the third moment (skew) as 0, and the fourth moment (kurtosis) as 1.
And with that, the machinery we need to prove the CLT is in place.
Let X_1, X_2,…,X_n be ’n’ i. i. d. random variables that form a random sample of size ’n’. Assume that we’ve drawn this sample from a population that has a mean μ and variance σ².
Let X_bar_n be the sample mean:

Let Z_bar_n be the standardized sample mean:

The Central Limit Theorem states that as ‘n’ tends to infinity, Z_bar_n converges in distribution to N(0, 1), i.e. the CDF of Z_bar_n becomes identical to the CDF of N(0, 1) which is often represented by the Greek letter ϕ (phi):

To prove this statement, we’ll use the property of the MGF (see Eq. 5) that if the MGFs of X and Y are identical, then so are their CDFs. Here, it’ll be sufficient to show that as n tends to infinity, the MGF of Z_bar_n converges to the MGF of N(0, 1) which as we know (see Eq. 8) is ‘e’ to the power t²/2. In short, we’d want to prove the following identity:

Let’s define a random variable Z_k as follows:

We’ll now express the standardized mean Z_bar_n in terms of Z_k as shown below:

Next, we apply the MGF operator on both sides of Eq. (9):

By construction, Z_1/√n, Z_2/√n, …, Z_n/√n are independent random variables. So we can use property (7a) of MGFs which expresses the MGF of the sum of n independent random variables:

By their definition, Z_1/√n, Z_2/√n, …, Z_n/√n are also identical random variables. So we award ourselves the liberty to assume the following:
Z_1/√n = Z_2/√n = … = Z_n/√n = Z/√n.
Therefore using property (7b) we get:

Finally, we’ll also use the property (6) to express the MGF of a random variable (in this case, Z) that is scaled by a constant (in this case, 1/√n) as follows:

With that, we have converted our original goal of finding the MGF of Z_bar_n into the goal of finding the MGF of Z/√n.
M_Z(t/√n) is a function like any other function that takes (t/√n) as a parameter. So we can create a Taylor series expansion of M_Z(t/√n) at t = 0 as follows:

Next, we split this expansion into two parts. The first part is a finite series of three terms corresponding to k = 0, k = 1, and k = 2. The second part is the remainder of the infinite series:

In the above series, M⁰, M¹, M², etc. are the 0-th, 1st, 2nd, and so on derivatives of the Moment Generating Function M_Z(t/√n) evaluated at (t/√n) = 0. We’ve seen that these derivatives of the MGF happen to be the 0-th, 1st, 2nd, etc. moments of Z.
The 0-th moment, M⁰(0), is always 1. Recall that Z is, by its construction, a standard normal random variable. Hence, its first moment (mean), M¹(0), is 0, and its second moment (variance), M²(0), is 1. With these values in hand, we can express the above Taylor series expansion as follows:

Another way to express the above expansion of M_Z is as the sum of a Taylor polynomial of order 2 which captures the first three terms of the expansion, and a residue term that captures the summation:

We’ve already evaluated the order-2 Taylor polynomial. So our task of finding the MGF of Z is now further reduced to calculating the remainder term R_2.
Before we tackle the task of computing R_2, let’s step back and review what we want to prove. We wish to prove that as the sample size ‘n’ tends to infinity, the standardized sample mean Z_bar_n converges in distribution to the standard normal random variable N(0, 1):

To prove this we realized that it was sufficient to prove that the MGF of Z_bar_n will converge to the MGF of N(0, 1) as n tends to infinity.

And that led us on a quest to find the MGF of Z_bar_n shown first in Eq. (10), and which I am reproducing below for reference:

But it is really the limit of this MGF as n tends to infinity that we not only wish to calculate, but also show it to be equal to e to the power t²/2.
To make it to that goal, we’ll unpack and simplify the contents of Eq. (10) by sequentially applying result (12) followed by result (11) as follows:

Here we come to an uncomfortable place in our proof. Look at the equation on the last line in the above panel. You cannot just force the limit on the R.H.S. into the large bracket and zero out the yellow term. The trouble with making such a misinformed move is that there is an ‘n’ looming large in the exponent of the large bracket — the very n that wants to march away to infinity. But now get this: I said you cannot force the limit into the large bracket. I never said you cannot sneak it in.
So we shall make a sly move. We’ll show that the remainder term R_2 colored in yellow independently converges to zero as n tends to infinity no matter what its exponent is. If we succeed in that endeavor, common-sense reasoning suggests that it will be ‘legal’ to extinguish it out of the R.H.S., exponent or no exponent.
To show this, we’ll use Taylor’s theorem which I introduced in Eq. (1), and which I am reproducing below for your reference:

We’ll bring this theorem to bear upon our pursuit by setting x to (t/√n), and r to 2 as follows:

Next, we set a = 0, which instantly allows us to switch the limit:
(t/√n) → 0, to,
n → ∞, as follows:

Now we make an important and not entirely obvious observation. In the above limit, notice how the L.H.S. will tend to zero as long as n tends to infinity independent of what value t has as long as it’s finite. In other words, the L.H.S. will tend to zero for any finite value of t since the limiting behavior is driven entirely by the (√n)² in the denominator. With this revelation comes the luxury to drop t² from the denominator without changing the limiting behavior of the L.H.S. And while we’re at it, let’s also swing over the (√n)² to the numerator as follows:

Let this result hang in your mind for a few seconds, for you’ll need it shortly. Meanwhile, let’s return to the limit of the MGF of Z_bar_n as n tends to infinity. We’ll make some more progress on simplifying the R.H.S of this limit, and then sculpting it into a certain shape:

It may not look like it, but with Eq. (14), we are literally two steps away from proving the Central Limit Theorem.
All thanks to Jacob Bernoulli’s blast-from-the-past discovery of the product-series based formula for ‘e’.
So this will be the point to fetch a few balloons, confetti, party horns or whatever.
Ready?
Here, we go:
We’ll use Eq. (13) to extinguish the green colored term in Eq. (14):

Next we’ll use the following infinite product series for (e to the power x):

Get your party horns ready.
In the above equation, set x = t²/2 and substitute this result in the R.H.S. of Eq. (15), and you have proved the Central Limit Theorem:


G. Casella, R. L. Berger, “Statistical inference”, 2nd edition, Cengage Learning, 2018
All images and videos in this article are copyright Sachin Date under CC-BY-NC-SA, unless a different source and copyright are mentioned underneath the image or video.
To the extent required by trademark laws, this article acknowledges Mars and NeRds to be the registered trademarks of the respective owning companies.
Thanks for reading! If you liked this article, please follow me to receive more content on statistics and statistical modeling.
A Proof of the Central Limit Theorem was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
A Proof of the Central Limit Theorem
Go Here to Read this Fast! A Proof of the Central Limit Theorem


In the previous post on this topic, Setting A Dockerized Python Environment—The Hard Way, we saw how to set up a dockerized Python development environment via the command line interface (CLI). In this post, we will review a more elegant and robust approach for setting up a dockerized Python development environment using VScode and the Dev Containers extension.
Related articles:
Setting A Dockerized Python Environment — The Hard Way
By the end of this tutorial, you will be able to set up a simple Python development environment with VScode and the Dev Containers extension.

To follow along with this tutorial, you will need the following:
Throughout this tutorial, we will use the official Python image — python:3.1o.
All the code examples in this post are available here:
GitHub – RamiKrispin/vscode-python-medium: Supporting code for Medium Article
Before getting started, let’s explain what the Dev Containers extension is and when you should consider using it.
In a nutshell, the VScode Dev Containers extension enables you to open an isolated VScode session inside a docker container seamlessly. The level of isolation includes the following three layers:
The devcontainer.json file defines the session settings, enabling us to set and define the above three layers.
To set and launch your project folder inside a container with the Dev Containers extension, you will need the following two components:
The below diagram describes the Dev Containers general architecture:
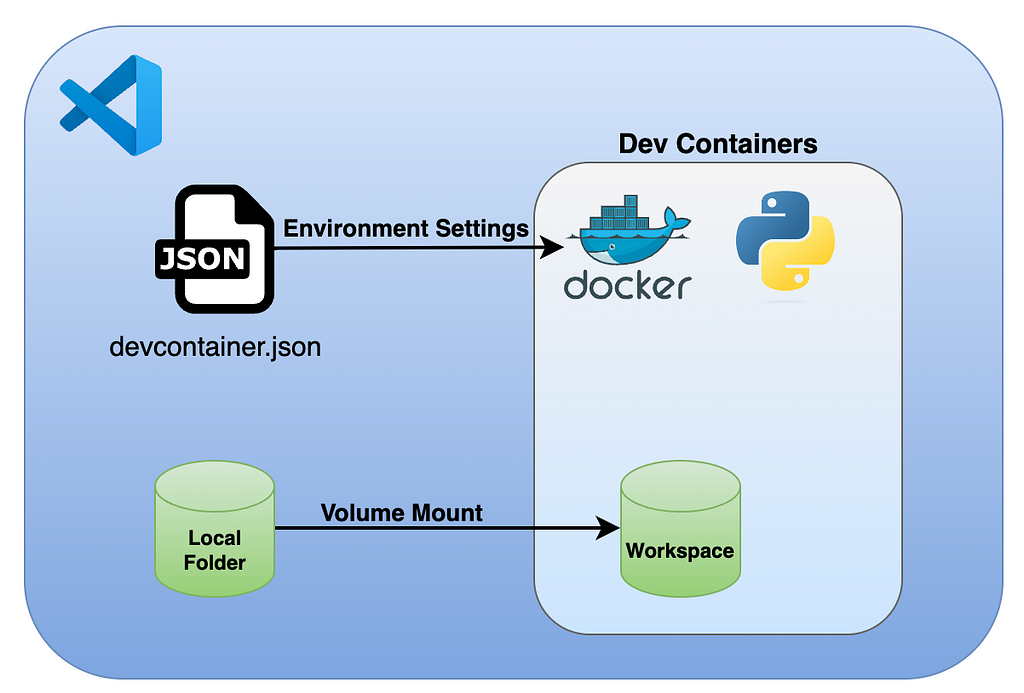
Upon launch, the Dev Containers extension spins a new VScode session inside a container. By default, it mounts the local folder to the container, which enables us to keep the code persistent and sync with our local folder. You can mount additional folders, but this is outside the scope of this tutorial.
In the next section, we will see how to set up a Python environment with the devcontainer.json file.
Before getting started with the devcontainer.json settings, let’s first define the scope of the development environment. It should include the following features:
In the following sections, we will dive into the core functionality of the devcontainer.json file. We will start with a minimalist Python environment and demonstrate how to customize it by adding different customization layers.
The main requirement for launching a containerized session with the Dev Containers extension is to define the image settings. There are two approaches for setting the image:
Depending on the use cases, each method has its own pros and cons. You should consider using the image argument when you have an image that fully meets the environment requirements. Likewise, a good use case for the build argument is when you have a base image but need to add minor customization settings.
In the next section, we will start with a simple example of launching a Python environment using the image argument to import the official Python image (python:3.10).
The below devcontainer.json file provides a simple example for setting up a Python environment. It uses the image argument to define the python:3.10 image as the session environment:
devcontainer.json
{
"name": "Python Development Environment",
"image": "python:3.10"
}
The name argument defines the environment name. In this case, we set it as Python Development Environment.
Before launching the environment, please make sure:
.
└── .devcontainer
└── devcontainer.json
The code for this example is available here.
To launch a session, click the Dev Container >< symbol on the bottom left and select the Reopen in Container option as demonstrated in the screenshot below:
Note that during the first launch time of the session, the Dev Containers extension will look for the image that was defined by the image argument (in this case — python:3.10). If the image is not available locally, it will pull it from Docker Hub, and it might take a few minutes. Afterward, it should take a few seconds to launch the session.
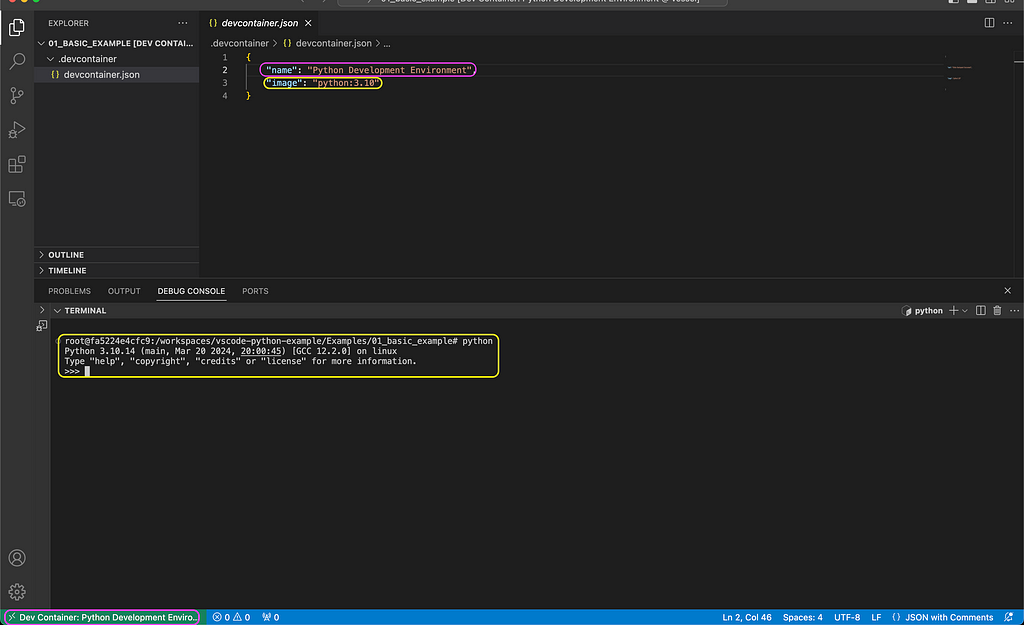
In the above screenshot, you can see the mapping between the devcontainer.json arguments and the session settings. The session name is now available on the bottom right (marked in purple) and aligned with the value of the name argument. Likewise, the session is now running inside the python:3.10 container, and you can launch Python from the terminal.
The Python container comes with the default Python libraries. In the following section, we will see how we can add more layers on top of the Python base image with the build argument.
Let’s now customize the above environment by modifying the devcontainer.json. We will replace the image argument with thebuild argument. The build argument enables us to build the image during the session launch time with a Dockerfile and pass arguments to the docker build function. We will follow the same approach as demonstrated in this post to set the Python environment:
We will use the following Dockerfile to set the Python environment:
Dockerfile
FROM python:3.10
ARG PYTHON_ENV=my_env
ENV PYTHON_ENV=$PYTHON_ENV
RUN mkdir requirements
COPY requirements.txt set_python_env.sh /requirements/
RUN bash ./requirements/set_python_env.sh $PYTHON_ENV
We use the FROM argument to import the Python image, and the ARG and ENVarguments to set the virtual environment as an argument and environment variable. In addition, we use the following two helper files to set a virtual environment and install the required libraries:
requirements.txt
wheel==0.40.0
pandas==2.0.3
ipykernel
ipywidgets
jupyter
set_python_env.sh
#!/usr/bin/env bash
PYTHON_ENV=$1
python3 -m venv /opt/$PYTHON_ENV
&& export PATH=/opt/$PYTHON_ENV/bin:$PATH
&& echo "source /opt/$PYTHON_ENV/bin/activate" >> ~/.bashrc
source /opt/$PYTHON_ENV/bin/activate
pip3 install -r ./requirements/requirements.txt
Last but not least, we will use the following test file to evaluate if the Pandas library was installed properly and print Hello World! message:
test1.py
import pandas as pd
print("Hello World!")
Let’s make the changes in the devcontainer.json file, and replace the image argument with the build argument:
devcontainer.json
{
"name": "Python Development Environment",
"build": {
"dockerfile": "Dockerfile",
"context": ".",
"args": {
"PYTHON_ENV": "my_python_dev"
}
}
}
The files for this example are available here.
The build sub-arguments enable us to customize the image build by passing arguments to the docker build function. We use the following arguments to build the image:
You should have the three files — Dockerfile, requirements.txt, and set_python_env.sh stored under the .devcontainer folder, along with the devcontainer.json file:
.
├── .devcontainer
│ ├── Dockerfile
│ ├── devcontainer.json
│ ├── requirements.txt
│ └── set_python_env.sh
└── test2.py
Let’s now launch the session using the new settings and test it with the test1.py file:
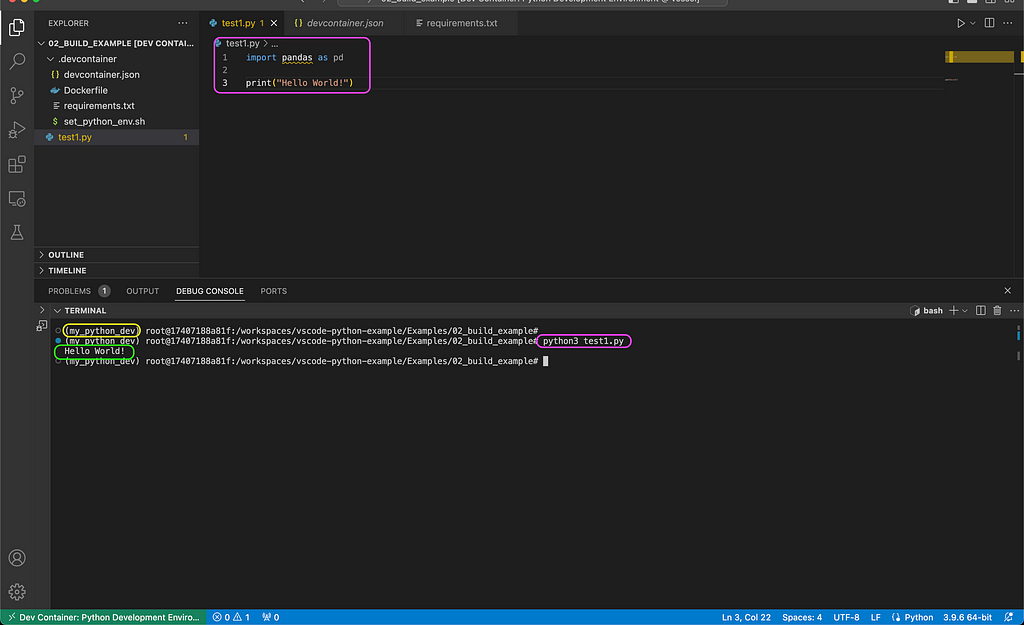
As you can notice in the above screenshot, we were able to successfully run the test script from the terminal (marked in purple), and it printed the Hello World! message as expected (marked in green). In addition, the virtual environment we set in the image (my_python_dev) is loaded by default (marked in yellow).
In the next section, we will see how to customize the VScode settings of the Dev Containers session.
One of the great features of the Dev Containers extension is that it isolates the session setting from the main VScode settings. This means you can fully customize your VScode settings at the project level. It extends the development environment’s reproducibility beyond the Python or OS settings. Last but not least, it makes collaboration with others or working on multiple machines seamless and efficient.
We will conclude this tutorial with the next example, where we see how to customize the VScode settings with the customizations argument. We will add the argument to the previous example and use the vscode sub-argument to set the environment default Python interpreter and the required extensions:
devcontainer.json
{
"name": "Python Development Environment",
"build": {
"dockerfile": "Dockerfile",
"context": ".",
"args": {
"PYTHON_ENV": "my_python_dev"
}
},
"customizations": {
"vscode": {
"settings": {
"python.defaultInterpreterPath": "/opt/my_python_dev/bin/python3",
"python.selectInterpreter": "/opt/my_python_dev/bin/python3"
},
"extensions": [
"ms-python.python",
"ms-toolsai.jupyter"
]
}
}
}
The files for this example are available here.
We use the settings argument to define the Python virtual environment as defined in the image. In addition, we use the extensions argument for installing the Python and Jupyter supporting extensions.
Note: The path of the the virtual environment defined by the type of applicationas that was used to set the environment. As we use venv and named it as my_python_dev, the path is opt/my_python_dev/bin/python3.
After we add the Python extension, we can launch Python scripts using the extension plug-in, as demonstrated in the screenshot below. In addition, we can execute the Python code leveraging the Juptyer extension, in an interactive mode:
In this tutorial, we reviewed how to set a dockerized Python environment with VScode and the Dev Containers extension. The Dev Containers extension makes the integration of containers with the development workflow seamless and efficient. We saw how, with a few simple steps, we can set and customize a dockerized Python environment using the devcontainer.json file. We reviewed the two approaches for setting the session image with the image and build arguments and setting extensions with the customizations argument. There are additional customization options that were not covered in this tutorial, and I recommend checking them:
If you are interested in diving into more details, I recommend checking this tutorial:
Setting A Dockerized Python Environment — The Elegant Way was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Setting A Dockerized Python Environment — The Elegant Way
Go Here to Read this Fast! Setting A Dockerized Python Environment — The Elegant Way



In the realm of Natural Language Processing (NLP), cutting-edge Large Language Models (LLMs) offer remarkable few-shot learning and reasoning capabilities. However, the computational demands and latency associated with these models can sometimes render them impractical for certain applications. If your goal, for instance, is to develop a translation service, you probably don’t require your back-end LLM to possess the ability to crack jokes or explain quantum physics to a kindergartner. This highlights the demand for specialized, smaller-scale models.
A viable solution to this challenge is to construct tailored LLMs that cater precisely to your specific use case. This involves annotating significant volumes of data and then fine-tuning a more compact model like Tiny-llama to suit your requirements. Such an approach not only ensures that the model aligns closely with your needs but also mitigates the computational and deployment expenses associated with larger LLMs. However, one must acknowledge the downside of this method: the process of data annotation is often laborious and time-consuming.
To address this bottleneck, an alternative emerges in the form of knowledge distillation. Instead of relying solely on manual labeling, this approach leverages the capabilities of a very large language model along with targeted prompting to generate labeled data automatically. Subsequently, a smaller model can be fine-tuned using this distilled knowledge, thereby streamlining the model development process while maintaining performance.
In this post, we will work trough this exact same scenario applied to building a model for multi-language grammatical error correction.
Our goal is to detect and correct grammatical errors within a sentence. For instance:
Here’s how we’re going to distill the knowledge from our teacher model to our student model:
The data we use is from huggingface datasets “`juancavallotti/multilingual-gec““ where we only use the labels for evaluation and not for training. [Licensed under Apache 2]
This data can be loaded as follows:
from datasets import load_dataset
data = load_dataset("juancavallotti/multilingual-gec", split="train")
We’re employing the LLama 2–70B as our teacher model. The teacher model is what will produce the pseudo-labels that will be used for the training. This powerful LLM is hosted on AnyScale’s pay-per-use API. AnyScale offers a $10 credit, allowing you to explore and utilize the model without incurring any costs initially. As an alternative you can also use OpenAI or Anthropic’s API.
We generate pseudo-labels for around 5000 samples. It costs 1.2 dollars.
You can call this API like this:
from openai import OpenAI
BASE_URL = "https://api.endpoints.anyscale.com/v1"
BASE_MODEL = "meta-llama/Llama-2-70b-chat-hf"
BASE_CLIENT = OpenAI(base_url=BASE_URL, api_key=API_KEY)
def process_call(prompt):
completion = BASE_CLIENT.completions.create(
model=BASE_MODEL,
prompt=prompt,
max_tokens=100,
temperature=0,
)
result = completion.model_dump()
return result["choices"][0]["text"].strip()
We use a simple few-shot prompting technique using the LLama 2 prompt template. This allows the LLM to understand what is the expected output and generally improves the quality of the result.
<s>[INST]
Your role is to correct all grammatical errors in the input text. Only answer with the corrected text and nothing else.
Text: Il est très importante de parler une langue étrangère.
[/INST]
Output: Il est très important de parler une langue étrangère.</s>
[INST]
Text: Nadie dise ezo.
[/INST]
Output: Nadie dice eso.</s>
[INST]
Text: What is your favorite part of being a member of SWE RMS?
[/INST]
Output: What is your favorite part of being a member of SWE RMS?</s>
[INST]
Text: I looked, at the schedule.
[/INST]
Output: I looked at the schedule.</s>
[INST]
Text: $text
[/INST]
Output:
We are using Tiny-LLama as our student model. The student model is what we will “train” on the grammar correction task using the pseudo-labels from the teacher model. Despite its smaller scale with 1 billion parameters, it’s highly efficient. Tiny-LLama can run on consumer GPUs with just a few gigabytes of memory.
This model can be run as a HuggingFace Pipeline. We use BitsAndBytes for GPU quantization, this reduces the memory requirements of running LLMs.
from transformers import (
AutoModelForCausalLM,
AutoTokenizer,
BitsAndBytesConfig,
pipeline,
)
base_model_name = "TinyLlama/TinyLlama-1.1B-Chat-v1.0"
llama_tokenizer = AutoTokenizer.from_pretrained(
base_model_name, trust_remote_code=True
)
llama_tokenizer.padding_side = "right"
quant_config = BitsAndBytesConfig(
load_in_4bit=True,
bnb_4bit_quant_type="nf4",
bnb_4bit_compute_dtype=torch.float16,
bnb_4bit_use_double_quant=False,
)
# Model
model = AutoModelForCausalLM.from_pretrained(
base_model_name,
quantization_config=quant_config,
device_map={"": 0},
)
text_gen = pipeline(
task="text-generation",
model=model,
tokenizer=llama_tokenizer,
max_new_tokens=256,
do_sample=False,
return_full_text=False,
)
print(text_gen("Hello ! Who are you ?"))
You should get something like this in the output:
[{'generated_text': ' I am a writer, a poet, a musician, a dancer, a painter, a sculptor, a filmmaker, a photographer, a cartoonist, a journalist, a teacher, a student, a lover, a friend, a stranger, a human being, a cat, a dog, a bird, a tree, a rock, a sandstone, a mineral, a fossil, a plant, a fungus, a bacterium, a virus, a microbe, a parasite, a symbiosis, a symphony, a symmetry, a chaos, a harmony, a balance, a balance of forces, a balance of energies, a balance of opposites, a balance of opposing forces, a balance of opposing principles, a balance of opposing ideas, a balance of opposing emotions, a balance of opposing thoughts, a balance of opposing desires, a balance of opposing needs, a balance of opposing needs, a balance of opposing desires, a balance of opposing emotions, a balance of opposing principles, a balance of opposing forces, a balance of opposing energies, a balance of opposing symb'}]
We can also fine-tune it using HuggingFace libraries: PEFT and TRL. PEFT stands for “Parameter-Efficient Fine-Tuning” and it implements different types of low-rank adapter LLM fine-tuning methods. TRL stands for “Transformer Reinforcement Learning” and implements general fine-tuning workflows.
You can read all about it here: https://huggingface.co/docs/trl/main/en/lora_tuning_peft
The implementation uses QLoRa, an approach that is able to fine-tune adapter weights of a quantized version of the full model. This allows us to run the training with around 3Gb of VRam using a mini-batch size of 8 which makes it possible to run in most consumer grade GPUs.
LoRa are additive low rank adapter weights that are trained while freezing the backbone. It allows to build specialized models that can be trained with a much smaller VRam and disk space footprint. In our case, the weights are only 4.5 MB and include around one million parameters.
Here is the pseudo-code that shows how it works, full code is linked at the end of the post:
import torch
from peft import LoraConfig, get_peft_model, prepare_model_for_kbit_training
from transformers import (
AutoModelForCausalLM,
AutoTokenizer,
BitsAndBytesConfig,
TrainingArguments,
)
from trl import SFTTrainer
if __name__ == "__main__":
.
.
.
.
peft_parameters = LoraConfig(
lora_alpha=8,
lora_dropout=0.1,
r=8,
bias="none",
task_type="CAUSAL_LM",
# target_modules=target_modules,
)
base_model = prepare_model_for_kbit_training(base_model)
base_model = get_peft_model(base_model, peft_parameters)
# Training Params
train_params = TrainingArguments(
output_dir=str(BASE_PATH / "results_modified"),
num_train_epochs=EPOCHS,
per_device_train_batch_size=8,
gradient_accumulation_steps=1,
optim="paged_adamw_32bit",
save_steps=len(training_data) // 10,
logging_steps=len(training_data) // 100,
learning_rate=2e-4,
lr_scheduler_type="cosine",
warmup_steps=100,
weight_decay=0.05,
fp16=True,
max_steps=-1,
group_by_length=False,
max_grad_norm=0.3,
)
# Trainer
fine_tuning = SFTTrainer(
model=base_model,
train_dataset=training_data,
data_collator=collator,
peft_config=peft_parameters,
dataset_text_field="Why is this mandatory ?",
tokenizer=llama_tokenizer,
args=train_params,
max_seq_length=llama_tokenizer.model_max_length,
)
print(fine_tuning.model.print_trainable_parameters())
# Training
fine_tuning.train()
To evaluate whether or not this whole workflow works or not we can look at few outputs of the base Tiny-LLama versus the version distilled from LLama 2–70B’s output. So let’s see:
Example 1:
Corrupted input:
* We dont live in Australia Were just visiting
Base model output:
* We don’t live in Australia, We’re just visiting.
Distilled model output:
* We don’t live in Australia. We are just visiting.
Here the base model fixed some of the issues but messed up the punctuation.
Example 2:
Corrupted input:
* Je ai été surprise.
Base model output:
* I was surprised.
Distilled model output:
* J’ai été surprise.
Here the base model fixed the sentence but created an output in English instead of in the original french while the distilled model fixed it in French.
We can also compute the fraction of cases where the output of the model matches exactly with expected output. This metric is flawed as there can be multiple ways a sentence can be fixed (“It is very hard to get rid of bad habit.” can be corrected as “It is very hard to get rid of bad habits.” or “It is very hard to get rid of a bad habit.”) but it can serve as a good proxy of the quality of generation. We get the following scores:
LLama 2–70B: 42%
Base Tiny-LLama: 11%
Distilled Tiny-LLama: 31%
While we are still far from the performance of the teacher model, we were able to significantly improve the performance of the student model from 11% to 31%. The gap from 31% to 42% can be bridged by either using a larger distillation dataset or a bigger student model.
By distilling knowledge from a high-capacity teacher model, such as the LLama 2–70B, to a more compact student model like Tiny-LLama, we navigate the trade-offs between computational efficiency and task-specific accuracy. This process involves crafting prompts, acquiring unlabeled in-domain data, and fine-tuning the student model using pseudo-labels generated by the teacher model. This approach mitigates the computational and deployment expenses associated with larger LLMs.
The implementation showcased here, focusing on multi-language grammatical error correction, underscores the practicality and effectiveness of knowledge distillation. Despite the laborious and time-consuming nature of data annotation, distillation techniques offer a scalable solution by automating the generation of labeled data through targeted prompting. Moreover, advancements in model quantization and training methodologies, such as QLoRa and PeFt, further optimize the training of specialized models on consumer-grade GPUs.
Evaluation results demonstrate a notable improvement in the performance of the student model, transitioning from 11% accuracy to 31% exact match score, albeit still below the benchmark set by the teacher model at 42%. However, this progress underscores the efficacy of distillation techniques in bridging the gap between computational efficiency and task-specific accuracy.
Code: https://github.com/CVxTz/distill-llm
Clone the Abilities of Powerful LLMs into Small Local Models Using Knowledge Distillation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Clone the Abilities of Powerful LLMs into Small Local Models Using Knowledge Distillation


Originally appeared here:
Gradient makes LLM benchmarking cost-effective and effortless with AWS Inferentia


Originally appeared here:
Enable single sign-on access of Amazon SageMaker Canvas using AWS IAM Identity Center: Part 2
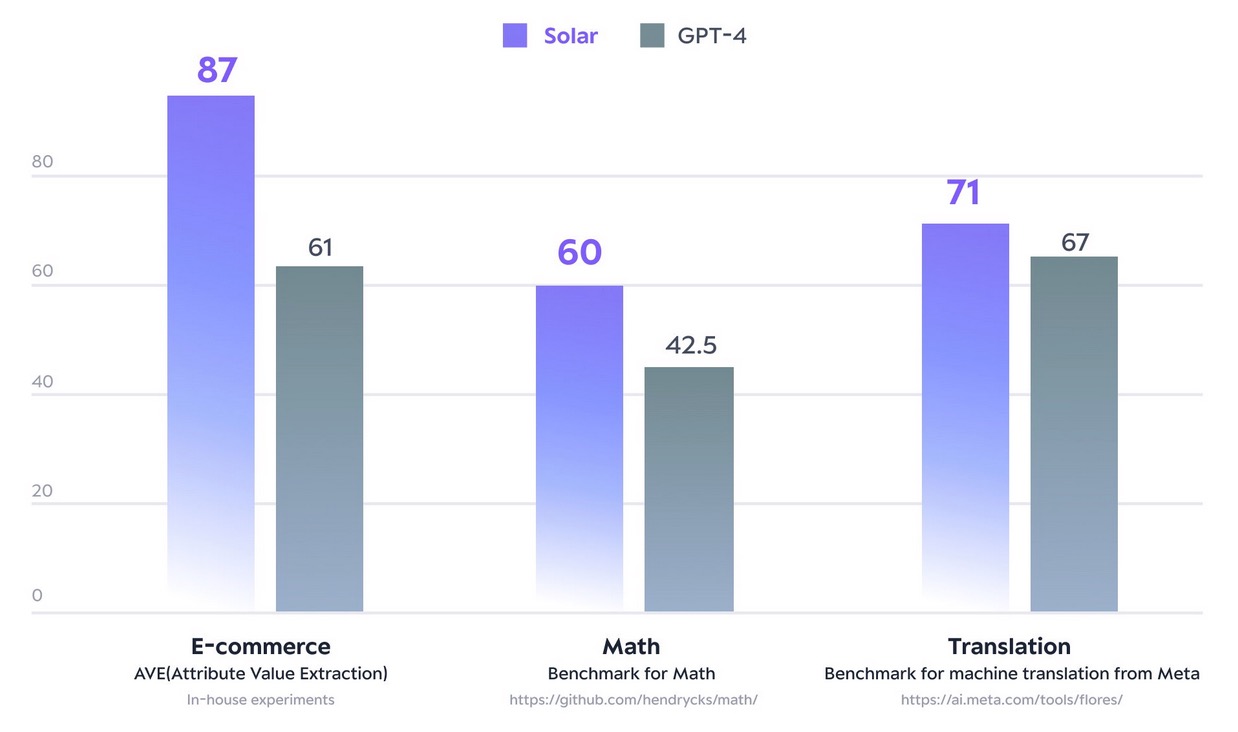

Originally appeared here:
Solar models from Upstage are now available in Amazon SageMaker JumpStart
Go Here to Read this Fast! Solar models from Upstage are now available in Amazon SageMaker JumpStart
Learn how to configure pytest in pyproject.toml to run doctests
Originally appeared here:
Configuring Pytest to Run Doctest
Go Here to Read this Fast! Configuring Pytest to Run Doctest


This article is meant to provide a simple approachable summary of studies that explored labelling data with LLMs¹. We will cover current views on annotating textual data with LLMs and also things to consider for your own projects.
Overview:

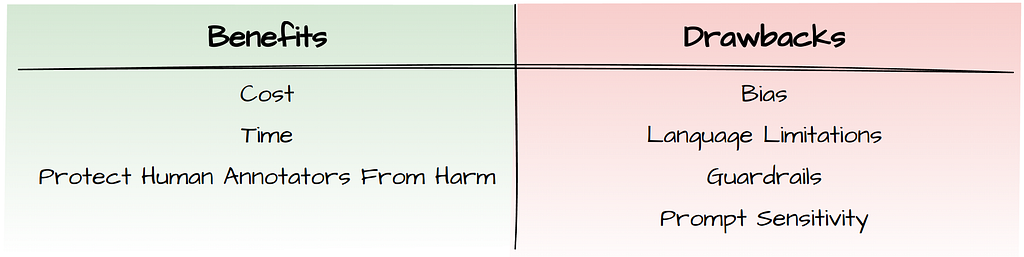
High quality labelled data creates the foundation for training and evaluating machine learning models across diverse tasks. The most common approach to annotating datasets right now is to hire crowd-workers (e.g. Amazon Mechanical Turk) or domain experts if specialised knowledge is required.
These approaches can be rather expensive and time-consuming, which is why a lot of people are now wondering if LLMs can handle data labelling well enough. Businesses with limited budgets could benefit from this by building specialised models that address their particular needs. In more sensitive domains like medicine, there’s potential to speed up the labelling process by having experts review and correct LLM labels rather than starting from scratch.
Additionally, researchers at Carnegie Mellon & Google find that people are motivated by the possibility of protecting human annotators from psychological harm caused during the labelling process (e.g hate-speech) as well as the diversification of opinions in the data.
Opinions are somewhat split amongst studies regarding the potential of LLMs as annotators. While some studies are optimistic about their capabilities, others remain sceptical. Table 1 provides an overview of the approach and results from twelve studies. You can find the source of these studies in the References (see end of this article).

The Number of Model Families highlights that most of the studies only test one model family and when we look at which model they used, we can see that almost all except for 2 studies used GPT. Study [7] is the only one which solely focuses on the exploration of open-source LLMs (Table 2).

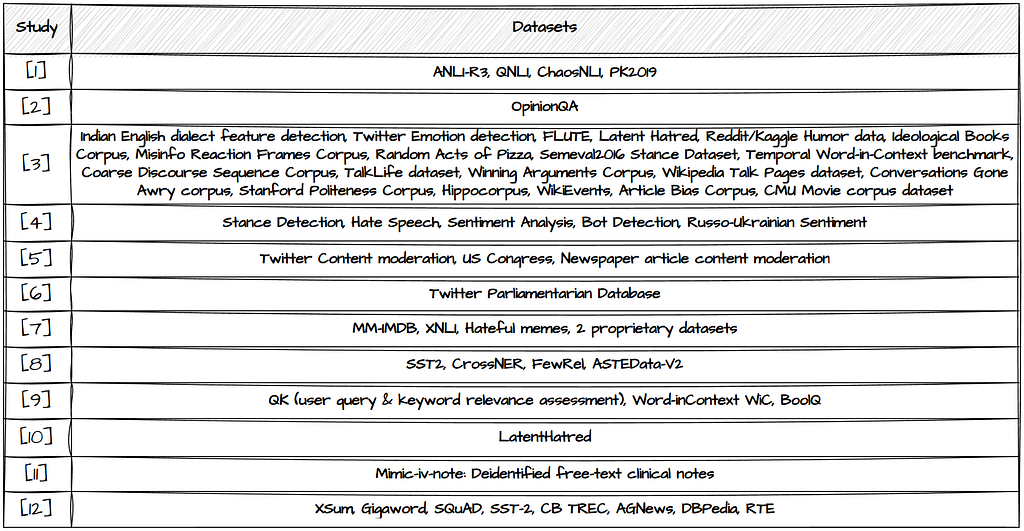
The third column of Table 1 contains the Number of Datasets that were used for labelling purposes. The different studies explore different tasks and thereby also a variety of datasets. Most explore the performance on more than one dataset. Study [3] stands out by testing LLM classification performance across 20 different datasets. More details on which datasets were used are shown in Table 3 below, and could help you spot the studies most relevant to you.
If you’re starting out with no labelled data at hand: Have a look at existing labelled datasets for tasks that are similar to your own use case and label the data with an LLM. Compare the LLM generated labels with the human labels by investigating the errors and potential issues in detail. This should give you an indication of how well the LLM will perform on your task and whether the time & cost savinngs can be justified.
A Perspectivist Approach simply means recognising that there is no one “right” way to understand a dataset or solve a problem. Different perspectives can reveal different insights or solutions. Whereas traditionally, most datasets are labelled using a majority voting approach, meaning that the most commonly chosen label is viewed as the ground truth:

In Table 1, the labelling approach is categorised based on whether the study uses a majority voting or perspectivist mindset. We can see that most of the studies take a majority voting approach towards their labelling efforts.
The last column summarises each study’s findings, with a check-mark indicating a tendency towards believing that LLMs can be helpful in the annotation process. While some are quite optimistic about their potential and suggest the replacement of human annotators, others see them more as a support tool rather than a substitute for humans. Regardless, even amongst these studies with a positive outlook, there are some tasks on which LLMs don’t perform well enough.
Additionally, three studies, two of which follow the perspectivist approach, conclude that they are not suited for labelling data. Another study (not included in the table) takes a different approach and shows that the current method of aligning LLMs via a single reward function doesn’t capture the diversity of preferences among different human subgroups, especially minority views.
Obtaining meaningful responses from LLMs can be a bit of a challenge. How do you then best prompt an LLM to label your data? As we can see from Table 1, the above studies explored either zero-shot or few-shot prompting, or both. Zero-shot prompting expects an answer from the LLM without having seen any examples in the prompt. Whereas few-shot prompting includes multiple examples in the prompt itself so that the LLM knows what a desired response looks like:
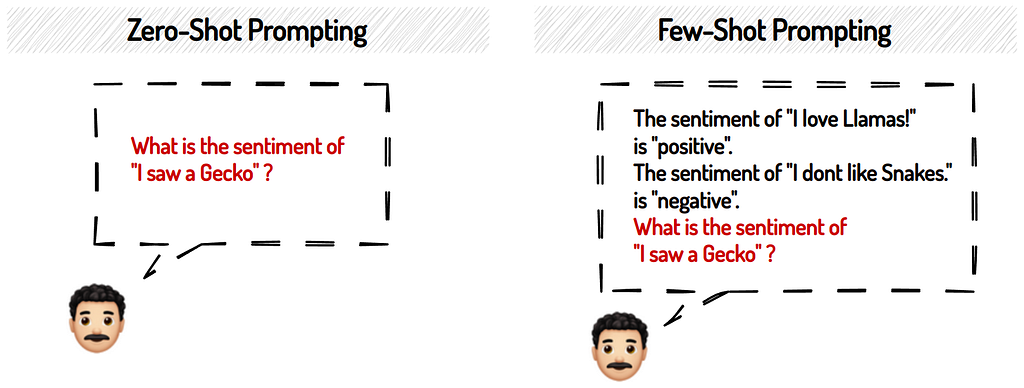
The studies differ in their views on which approach returns better results. Some resort to few-shot prompting on their tasks, others to zero-shot prompting. So you might want to explore what works best for your particular use case and model.
If you are wondering how to even start with good prompting Sander Schulhoff & Shyamal H Anadkat have created LearnPrompting which can help you with basics and also more advanced techniques.
LLMs are sensitive to minor modifications in the prompt. Changing one word of your prompt can affect the response. If you want to account for that variability to some degree you could approach it as in study [3]. First, they let a task expert provide the initial prompt. Then, using GPT, they generate 4 more with similar meaning and average the results over all 5 prompts. Or you could also explore moving away from hand-written prompts and try replacing them with signatures leaving it to DSPy to optimise the prompt for you as shown in Leonie Monigatti’s blog post.

Which model should you choose for labelling your dataset? There are a few factors to consider. Let’s briefly touch on some key considerations:
According to study [3] larger, instruction-tuned³ models show superior labelling performance. However, the study doesn’t evaluate bias in their results. Another research effort shows that bias tends to increase with both scale and ambiguous contexts. Several studies also warn about left-leaning tendencies and the limited capability to accurately represent the opinions of minority groups (e.g. older individuals or underrepresented religions). All in all, current LLMs show considerable cultural biases and respond with stereotyped views of minority individuals. Depending on your task and its aims, these are things to consider across every timeline in your project.

“By default, LLM responses tend to be more similar to the opinions of certain populations, such as those from the USA, and some European and South American countries” — quote from study [2]
A commonly mentioned parameter across most studies in Table 1 is the temperature parameter, which adjusts the “creativity” of the LLMs outputs. Studies [5] and [6] experiment with both higher and lower temperatures, and find that LLMs have higher consistency in responses with lower temperatures without sacrificing accuracy; therefore they recommend lower values for annotation tasks.
As we can see in Table 1, most of the studies measure the LLMs labelling performance on English datasets. Study [7] explores French, Dutch and English tasks and sees a considerable decline in performance with the non-English languages. Currently, LLMs perform better in English, but alternatives are underway to extend their benefits to non-English users. Two such initiatives include: YugoGPT (for Serbian, Croatian, Bosnian, Montenegrin) by Aleksa Gordić & Aya (101 different languages) by Cohere for AI.
Apart from simply requesting a label from the LLM, we can also ask it to provide an explanation for the chosen label. One of the studies [10] finds that GPT returns explanations that are comparable, if not more clear than those produced by humans. However, we also have researchers from Carnegie Mellon & Google highlighting that LLMs are not yet capable of simulating human decision making and don’t show human-like behavior in their choices. They find that instruction-tuned models show even less human-like behaviour and say that LLMs should not be used to substitute humans in the annotation pipeline. I would also caution the use of natural language explanations at this stage in time.
“Substitution undermines three values: the representation of participants’ interests; participants’ inclusion and empowerment in the development process” — quote from Agnew (2023)
This review is by no means an exhaustive comparison. If you have other sources that can contribute to the discussion or personal experience with LLM data labelling, please do share in the comments.
References
Footnotes
¹This is not a comprehensive review on all the literature out there but covers only papers I found whilst doing reading on this topic. Additionally, my focus was mostly on classification tasks.
²Given the pace of development in LLMs, there are now a lot more powerful models available compared to the ones tested in these studies.
³Instruction-tuned models are trained with a focus on understanding and generating accurate and coherent responses based on given instructions/prompts.
Can Large Language Models (LLMs) be used to label data? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Can Large Language Models (LLMs) be used to label data?
Go Here to Read this Fast! Can Large Language Models (LLMs) be used to label data?



“In the ancient land of DiTharos, there once lived a legend, called Sora. A legend that embodied the very essence of unlimited potential, encompassing the vastness and the magnificence of the skies.
When it soared high with its iridescent wings spanning vast expanses and light bouncing off its striking body, one could hear the words ‘Sora IS Sky’ echoing into the heavens. What made it a legend was not just its epic enormity but its power to harness the elements of light scattered in the swirling clouds. With its mighty strength, the magic that Sora created with a single twirl, was a sight to behold!
They say, Sora lives on, honing its skills and getting stronger with each passing day, ready to fly when the hour is golden. When you see a splash of crimson red in the sky today, you would know it’s a speck of the legend flying into the realms of light!”
This is a story I told my son about a mythical dragon that lived in a far away land. We called it ‘The Legend of Sora’. He really enjoyed it because Sora is big and strong, and illuminated the sky. Now of course, he doesn’t understand the idea of transformers and diffusion yet, he’s only four, but he does understand the idea of a magnanimous dragon that uses the power of light and rules over DiTharos.
And that story very closely resembles how our world’s Sora, Open AI’s text-to-video model emerged in the realm of AI and has taken the world by storm. In principle, Sora is a diffusion transformer (DiT) developed by William Peebles and Saining Xie in 2023.
In other words, it uses the idea of diffusion for predicting the videos and the strength of transformers for next-level scaling. To understand this further, let’s try to find the answer to these two questions:
Talking about the videos made by Sora, here is my favorite one of an adorable Dalmatian in the streets of Italy. How natural is its movement!
The prompt used for the video : “The camera directly faces colorful buildings in Burano Italy. An adorable dalmation looks through a window on a building on the ground floor. Many people are walking and cycling along the canal streets in front of the buildings.”
How did Sora do this?
Without any further ado, let’s dive into the details and look at how Sora creates these super-realistic videos based on text-prompts.
Thanks once again to Prof. Tom Yeh’s wonderful AI by Hand Series, we have this great piece on Sora for our discussion. (All the images below, unless otherwise noted, are by Prof. Tom Yeh from the above-mentioned LinkedIn post, which I have edited with his permission.)
So, here we go:
Our goal — Generate a video based on a text-prompt.
We are given:
For our example, can you guess what our text-prompt is going to be? You are right. It is “Sora is sky”. A diffusion step of t = 3 means we are adding noise or diffusing the model in three steps but for illustration we will stick to one in this example.
What is diffusion?
Diffusion mainly refers to the phenomenon of scattering of particles — think how we enjoy the soft sun rays making a peak from behind the clouds. This soft glow can be attributed to the scattering of sunlight as it passes through the cloud layer causing the rays to spread out in different directions.
The random motion of the particles drives this diffusion. And that is exactly what happens for diffusion models used in image generation. Random noise is added to the image causing the elements in the image to deviate from the original and thus making way for creating more refined images.
As we talk about diffusion in regards to image-models, the key idea to remember is ‘noise’.
The process begins here:
[1] Convert video into patches
When working with text-generation, the models break down the large corpus into small pieces called tokens and use these tokens for all the calculations. Similarly, Sora breaks down the video into smaller elements called visual patches to make the work simpler.
Since we are talking about a video, we are talking about images in multiple frames. In our example, we have four frames. Each of the four frames or matrices contain the pixels that create the image.

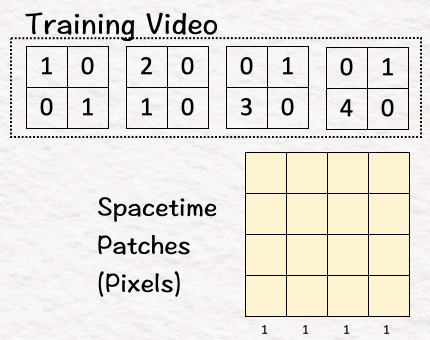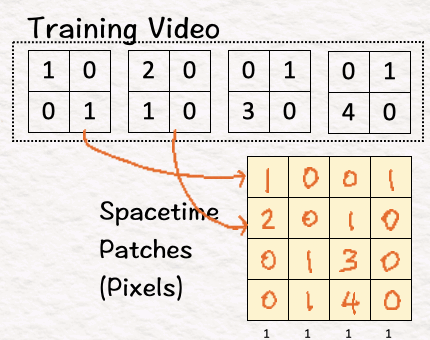
The first step here is to convert this training video into 4 spacetime patches as below:
[2] Reduce the dimension of these visual patches : Encoder
Next, dimension reduction. The idea of dimension reduction has existed for over a century now (Trivia : Principal Component Analysis, also known as PCA was introduced by Karl Pearson in 1901), but its significance hasn’t faded over time.
And Sora uses it too!
When we talk about Neural Networks, one of the fundamental ideas for dimension reduction is the encoder. Encoder, by its design, transforms high-dimensional data into lower-dimension by focusing on capturing the most relevant features of the data. Win-win on both sides: it increases the efficiency and speed of the computations while the algorithm gets useful data to work on.
Sora uses the same idea for converting the high-dimensional pixels into a lower-dimensional latent space. To do so, we multiply the patches with weights and biases, followed by ReLU.
Note:
Linear transformation : The input embedding vector is multiplied by the weight matrix W and
then added with the bias vector b,
z = Wx+b, where W is the weight matrix, x is our word embedding and b is the bias vector.
ReLU activation function : Next, we apply the ReLU to this intermediate z.
ReLU returns the element-wise maximum of the input and zero. Mathematically, h = max{0,z}.
The product of the transpose of the weight matrix W and bias b with the patches followed by ReLU gives us a latent space which is only a 2×4 matrix. Thus, by using the visual encoder the dimension of the ‘model’ is reduced from 4 (2x2x1) to 2 (2×1).
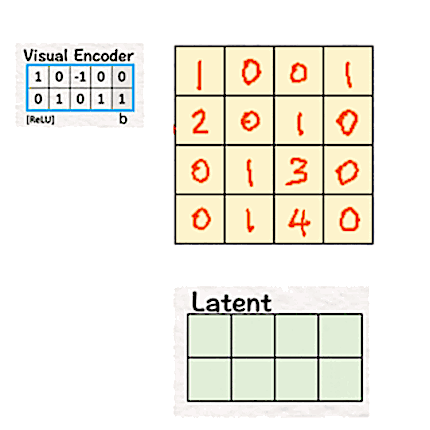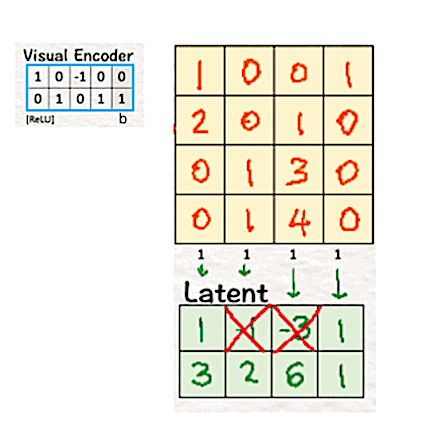
In the original DiT paper, this reduction is from 196,608 (256x256x3) to 4096 (32x32x4), which is huge. Imagine working with 196,608 pixels against working with 4096 — a 48 times reduction!
Right after this dimension reduction, we have one of the most significant steps in the entire process — diffusion.
[3] Diffuse the model with noise
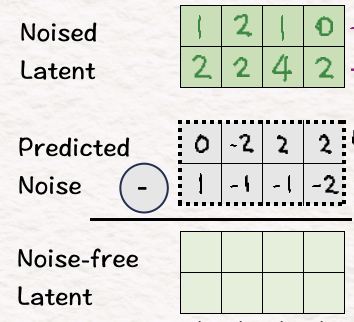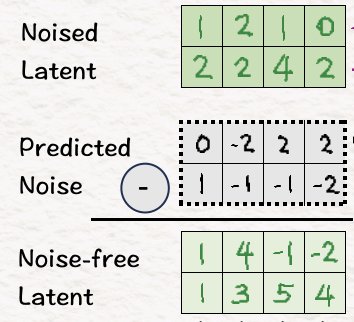
To introduce diffusion, we add sampled noise to the obtained latent features in the previous step to find the Noised Latent. The goal here is to ask the model to detect what the noise is.

This is in essence the idea of diffusion for image generation.
By adding noise to the image, the model is asked to guess what the noise is and what it looks like. In return, the model can generate a completely new image based on what it guessed and learnt from the noisy image.
It can also be seen relative to deleting a word from the language model and asking it to guess what the deleted word was.
Now that the training video has been reduced and diffused with noise, the next steps are to make use of the text-prompt to get a video as advocated by the prompt. We do this by conditioning with the adaptive norm layer.
What ‘conditioning’ essentially means is we try to influence the behavior of the model using the additional information we have available. For eg: since our prompt is ‘Sora is sky’, we would like for the model to focus on elements such as sky or clouds rather attaching importance on other concepts like a hat or a plant. Thus, an adaptive norm layer massages, in better terms — dynamically scales and shifts the data in the network based on the input it receives.
What is scale and shift?
Scale occurs when we multiply, for e.g. we may start with a variable A. When we multiply it with 2 suppose, we get 2*A which amplifies or scales the value of A up by 2. If we multiply it by ½, the value is scaled down by 0.5.
Shift is denoted by addition, for e.g. we may be walking on the number line. We start with 1 and we are asked to shift to 5. What do we do? We can either add 4 and get 1+4=5 or we could add a hundred 0.4s to get to 5, 1+(100*0.04 )= 5. It all depends on if we want to take bigger steps (4) or smaller steps (0.04) to reach our goal.
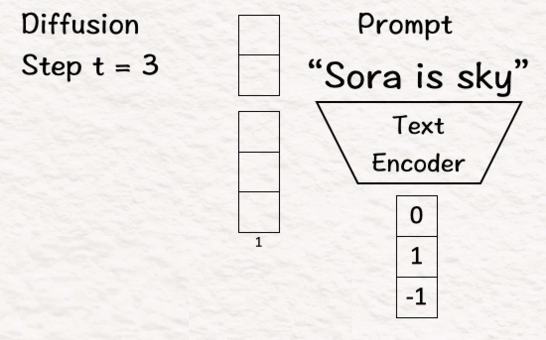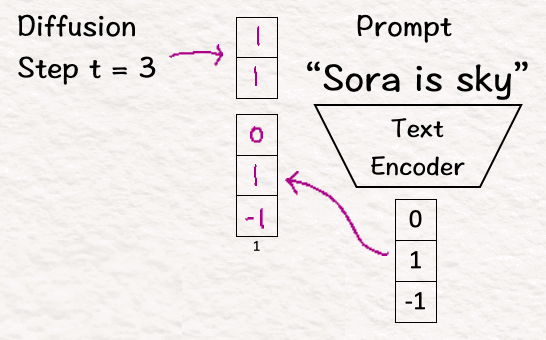
[4] Encode Conditions
To make use of the conditions, in our case the information we have for building the model, first we translate it into a form the model understands, i.e., vectors.
[5] Estimate Scale/Shift
Remember that here we use an ‘adaptive’ layer norm which implies that it adapts its values based on what the current conditions of the model are. Thus, to capture the correct essence of the data, we need to include the importance of each element in the data. And it is done by estimating the scale and shift.
For estimating these values for our model, we multiply the concatenated vector of prompt and diffusion step with the weight and add the bias to it. These weights and biases are learnable parameters which the model learns and updates.
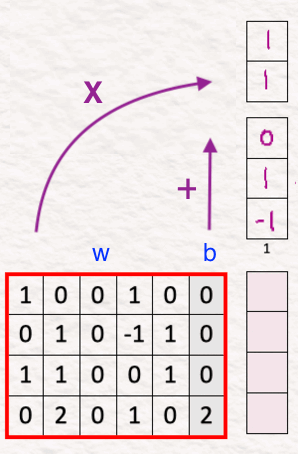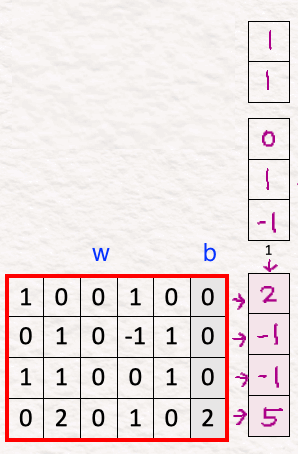
(Remark: The third element in the resultant vector, according to me, should be 1. It could be a small error in the original post but as humans we are allowed a bit of it, aren’t we? To maintain uniformity, I continue here with the values from the original post.)
The goal here is to estimate the scale [2,-1] and the shift [-1,5] (since our model size is 2, we have two scale and two shift parameters). We keep them under ‘X’ and ‘+’ respectively.
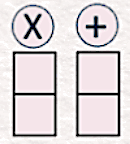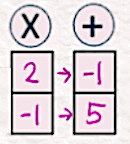
[6] Apply Scale/Shift
To apply the scale and shift obtained in the previous step, we multiply the noised latent in Step 3 by [2, -1] and shift it by adding [-1,5].

The result is the ‘conditioned’ noise latent.
The last three steps consist of adding the transformer element to the above diffusion and conditioning steps. This step help us find the noise as predicted by the model.
[7] Self-Attention
This is the critical idea behind transformers that make them so phenomenal!
What is self-attention?
It is a mechanism by which each word in a sentence analyzes every other word and measures how important they are to each other, making sense of the context and relationships in the text.
To enable self-attention, the conditioned noise latent is fed into the Query-Key function to obtain a self-attention matrix. The QK-values are omitted here for simplicity.
[8] Attention Pooling
Next, we multiply the conditioned noised latent with the self-attention matrix to obtain the attention weighted features.

[9] Point-wise Feed Forward Network
Once again returning back to the basics, we multiply the attention-weighted features with weights and biases to obtain the predicted noise.

The last bit now is to train the model using Mean Square Error between the predicted noise and the sampled noise (ground truth).
[10] Calculate the MSE loss gradients and update learnable parameters
Using the MSE loss gradients, we use backpropagation to update all the parameters that are learnable (for e.g. the weights and biases in the adaptive norm layer).

The encoder and decoder parameters are frozen and not learnable.
(Remark: The second element in the second row should be -1, a tiny error which makes things better).
[11] Denoise
Now that we are ready to generate new videos (yay!), we first need to remove the noise we had introduced. To do so, we subtract the predicted noise from the noise-latent to obtain noise-free latent.
Mind you, this is not the same as our original latent. Reason being we went through multiple conditioning and attention steps in between that included the context of our problem into the model. Thus, allowing the model a better feel for what its target should be while generating the video.
[12] Convert the latent space back to the pixels : Decoder
Just like we did for encoders, we multiply the latent space patches with weight and biases while followed by ReLU. We can observe here that after the work of the decoder, the model is back to the original dimension of 4 which was lowered to 2 when we had used the encoder.

[13] Time for the video!
The last step is to arrange the result from the above matrix into a sequence of frames which finally gives us our new video. Hooray!

And with that we come to the end of this supremely powerful technique. Congratulations, you have created a Sora video!
To summarize all that was said and done above, here are the 5 key points:
(Once you are done with the article, I suggest you to read the story at the beginning once more. Can you spot the similarities between Sora of DiTharos and Sora of our world?)
The kind of videos Sora has been able to produce, it is worth saying that the Diffusion-Transformer duo is lethal. Along with it, the idea of visual patches opens up an avenue for tinkering with a range of image resolutions, aspect ratios and durations, which allows for utmost experimentation.
Overall, it would not be wrong to say that this idea is seminal and without a doubt is here to stay. According to this New York Times article , Sora was named after the Japanese word for sky and to evoke the idea of limitless potential. And having witnessed its initial promise, it is true that Sora has definitely set a new frontier in AI. Now it remains to see how well it stands the test of safety and time.
As the legend of DiTharos goes — “Sora lives on, honing its skills and getting stronger with each passing day, ready to fly when the hour is golden!”
P.S. If you would like to work through this exercise on your own, here is a blank template for you to use.
Blank Template for hand-exercise
Now go have some fun with Sora in the land of ‘DiTharos’!
Deep Dive into Sora’s Diffusion Transformer (DiT) by Hand ✍︎ was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Deep Dive into Sora’s Diffusion Transformer (DiT) by Hand ✍︎
Go Here to Read this Fast! Deep Dive into Sora’s Diffusion Transformer (DiT) by Hand ✍︎