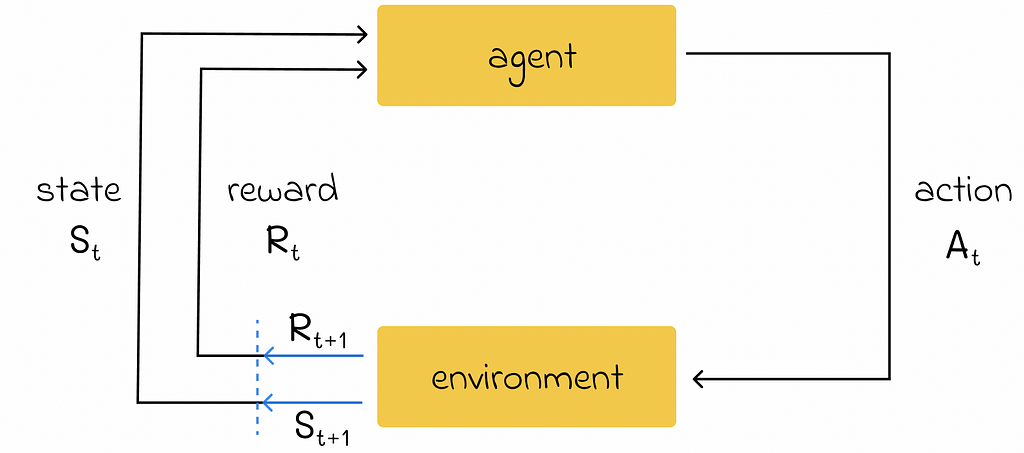
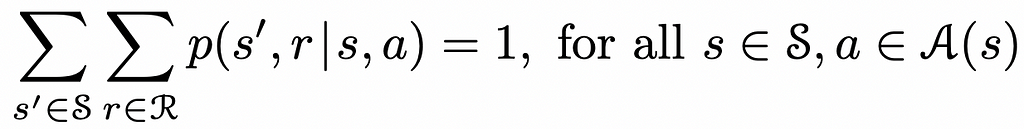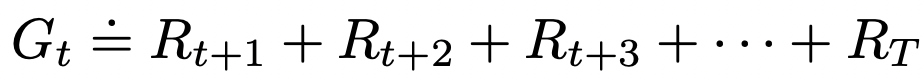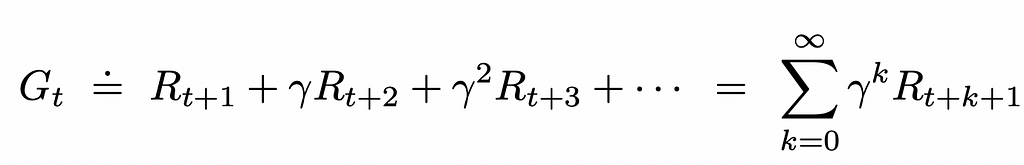Dive into CNN, the backbone of Computer Vision, understand its mathematics, implement it from scratch, and explore its applications

Index
· 2: The Math Behind CNN Architecture
∘ 2.1: Convolutional Layers
∘ 2.2: Stride
∘ 2.3: Padding
∘ 2.4: Multiple Filters and Depth
∘ 2.5: Weight Sharing
∘ 2.6: Feature Map Creation
∘ 2.7: Pooling Layers
∘ 2.8: Fully Connected Layers
· 3: Step-by-Step Guide to Building a CNN
∘ 3.1: Setting Up the Environment
∘ 3.2: Preparing the Data
∘ 3.3: Designing the CNN Model
∘ 3.4: Compiling the Model
∘ 3.5: Training the CNN
· 4: Improving Model Performance
∘ 4.1: Data Augmentation
∘ 4.2: Dropout
∘ 4.3: Batch Normalization
∘ 4.4: Transfer Learning
1: Introduction
Convolutional Neural Networks, or CNNs for short, are a big deal when it comes to working with images, like in photo recognition or sorting. They’re super good at picking up on the patterns and details in pictures automatically, which is why they’re a go-to for any project that deals with a bunch of images.
The cool thing about CNNs is that they don’t just mash all the image data into one big pile. Instead, they keep the layout of the image intact, which means they’re great at noticing the specific patterns and where they’re located. This approach is a game-changer because it lets CNNs handle the tricky parts of working with images much more smoothly.
One of the secret sauces of CNNs is something called convolutional layers. These layers move across the image and are able to spot different visual features, like lines, textures, and shapes. This beats the old-school way where people had to manually pick out these features, which was slow and often a bottleneck for getting things done. By having the network figure out these features on its own, CNNs not only get more accurate, they’re also simpler and can be used for a wider range of image-related tasks without much hassle.
2: The Math Behind CNN Architecture

The architecture of Convolutional Neural Networks (CNNs) is designed to mimic the way the human visual system processes images, making them especially powerful for tasks involving visual recognition and classification.
CNNs are composed of several types of layers, each serving a specific function in the image recognition process. The main layers include convolutional layers, activation functions, pooling layers, and fully connected layers. Together, these layers allow CNNs to detect features, reduce complexity, and make predictions.
2.1: Convolutional Layers
Convolutional layers are the cornerstone of Convolutional Neural Networks (CNNs), designed to automatically and efficiently extract spatial features like edges, textures, and shapes from images. Let’s dive deep into how convolutional layers work, including the underlying math.
The Convolution Operation

At its core, the convolution operation involves sliding a filter (or kernel) over the input image and computing the dot product of the filter values and the original pixel values at each position. The filter is a small matrix of weights, typically of size 3×3 or 5×5, which is trained to detect specific features in the image.
Mathematically, the convolution operation can be expressed as:

Where:
- S(i,j) is the output feature map.
- I is the input image.
- K is the kernel or filter.
- i,j are the coordinates on the feature map.
- m,n are the coordinates in the kernel.
- ∗ denotes the convolution operation.
This equation tells us that each element S(i,j) of the output feature map is the sum of the element-wise product of the kernel K and the portion of the input image I over which the kernel is currently positioned.
Now, consider a matrix of pixel values which will serve as input image. If it’s a grayscale image (image above), the matrix will have a single layer; for color images, there are typically three layers (RGB), but the operation is often performed separately on each layer.
The convolution operation apply a kernel (filter) to the matrix. Here the kernel is another matrix, smaller than the input image, with predefined dimensions (e.g., 3×3). The values in this matrix are the weights, which are learned during the training process. The kernel is designed to detect specific types of features, such as edges, textures, or patterns, from the input image. The kernel, then, strides (we will cover this operation in a moment) over the entire input image and performing element-wise multiplication followed by a sum.
From the convolution operation, we will get the output feature map. It’s a new matrix where each element represents the presence and intensity of a feature detected by the kernel at a specific location in the input image.
2.2: Stride

Stride is a crucial concept in the architecture of CNNs, particularly within the convolutional layers. It fundamentally influences how the kernel, traverses across the input image or feature map.
The stride specifies the number of pixels by which we move the filter across the input image or feature map in each step. It is applied both horizontally and vertically. A stride of 1 means the filter moves one pixel at a time, ensuring a detailed and dense scanning of the input. Larger strides result in the filter skipping pixels, leading to broader and less dense coverage.
The stride plays a direct role in determining the dimensions of the output feature map:
- With a Stride of 1: The filter moves across every pixel, often resulting in an output feature map that is relatively large or similar in size to the input, depending on padding, which we will talk about in the next section.
- With a Larger Stride: The filter skips over pixels, which means it covers the input in fewer steps. This leads to a smaller output feature map since each step covers a larger area of the input with less overlap between positions where the filter is applied.
Mathematical Representation
The size of the output feature map (W_out, H_out) can be calculated from the input size (W_in, H_in), filter size (F), stride (S), and padding (P) using the formula:

where:
- W_out and H_out are the width and height of the output feature map, respectively.
- W_in and H_in are the width and height of the input, respectively.
- F is the size of the filter.
- S is the stride.
- P is the padding.
A larger stride increases the field of view of each application of the filter, allowing the network to capture more global features of the input with fewer parameters.
Using a larger stride reduces the computational load and memory usage since it decreases the size of the output feature map and, consequently, the number of operations required for convolution.
A trade-off exists between spatial resolution and coverage. A smaller stride preserves spatial resolution and is better for detecting fine-grained features, while a larger stride offers broader coverage of the input at the expense of detail.
2.3: Padding
Padding plays a critical role in shaping the network’s architecture by influencing the spatial dimensions of the output feature maps.
It involves adding layers of zeros (or other values, but zeros are most common) around the border of the input image or feature map before applying the convolution operation. This technique can be applied for various reasons, the most prominent being to control the size of the output feature maps and to allow the convolutional filters to have access to the edge pixels of the input.
Therefore, our input image will now look like this:

You can notice how our previous 8×8 matrix is now a 10×10 matrix, as we added a layer of 0s around it.
Without padding, each convolution operation reduces the size of the feature map. Padding allows us to apply filters to the input without shrinking its spatial dimensions, preserving more information, especially for deeper networks where many convolutional layers are applied sequentially.
By padding the input, filters can properly process the edge pixels of the image, ensuring that features located at the borders are adequately captured and utilized in the network’s learning process.
There are two main types of padding:
Valid Padding (No Padding)
In this case, no padding is applied to the input. The convolution operation is performed only where the filter fully fits within the bounds of the input. This usually results in a reduction of the output feature map size.
Same Padding
With the same padding, enough zeros are added to the edges of the input to ensure that the output feature map has the same dimensions as the input (when the stride is 1). This is particularly useful for designing networks where the input and output sizes need to be consistent.
The effect of padding on the output feature map size can be captured by adjusting the formula used to calculate the dimensions of the output feature map:

where:
- W_out and H_out are the width and height of the output feature map, respectively.
- W_in and H_in are the width and height of the input, respectively.
- F is the size of the filter/kernel.
- S is the stride.
- P is the amount of padding added to each side of the input.
While padding helps in maintaining the spatial dimensions of the input through the layers, excessive padding might lead to computational inefficiency and an increase in the model’s complexity by adding more non-informative inputs (zeros) into the computation.
The choice between valid and same padding typically depends on the specific requirements of the application, such as the importance of preserving the spatial dimensions of the input or the need to minimize computational overhead.
2.4: Multiple Filters and Depth
CNNs employ multiple filters at each convolutional layer to capture a wide array of features from the input image or feature map. This multiplicity and the resultant depth are central to the network’s ability to process visual information in a comprehensive and nuanced manner.
Each filter in a convolutional layer is designed to detect different features or patterns in the input, such as edges, colors, textures, or more complex shapes in deeper layers. By using multiple filters, a CNN can simultaneously look for various features at each layer, enriching the representation of the input data.
The output of a convolutional layer with multiple filters is a stack of feature maps, one for each filter. This stack forms a three-dimensional volume where the depth corresponds to the number of filters used. This depth is crucial for building a hierarchical representation of the data, allowing subsequent layers to detect increasingly abstract features by combining the outputs of previous layers.
How Multiple Filters Achieve Depth
As the input image or feature map is processed, each filter slides across it, performing the convolution operation. Despite sharing the same input, each filter applies its unique weights, producing a distinct feature map that highlights different aspects of the input.
The individual feature maps generated by each filter are stacked along the depth dimension, forming a 3D volume. This volume encapsulates the diverse features detected by the filters, providing a rich, multi-faceted representation of the input.
The depth of the convolutional layer — determined by the number of filters — enables the network to capture a broad spectrum of features. Early layers might capture basic features like edges and textures, while deeper layers can interpret complex patterns by combining these basic features, thanks to the network’s depth.
Implications of Depth
More filters mean a deeper network with a higher capacity to learn complex features. However, this also increases the network’s computational complexity and the amount of training data needed to learn effectively.
Each filter adds parameters to the model (the weights that define the filter). While more filters increase the network’s expressive power, they also raise the total number of parameters, which can impact training efficiency and the risk of overfitting.
The allocation of filters across layers is strategic. Layers closer to the input might have fewer, more general filters, while deeper layers may use more filters to capture the complexity and variability of higher-order features within the data.
2.5: Weight Sharing
Weight sharing significantly enhances CNNs’ efficiency and effectiveness, especially in processing visual information. This concept is pivotal in allowing the model to detect features regardless of their spatial location in the input image.
In the context of CNNs, weight sharing refers to using the same filter (and thus the same set of weights) across the entire input image or feature map. Instead of learning a unique set of weights for every possible location, a single filter scans the entire image, applying the same weights at each position. This operation is repeated for each filter in the convolutional layer.
By reusing the same set of weights across different parts of the input image, weight sharing dramatically reduces the number of parameters in the model. This makes CNNs much more parameter-efficient compared to fully connected networks, especially when dealing with large input sizes.
Weight sharing enables the network to detect features regardless of their position in the input image. If a filter learns to recognize an edge or a specific pattern, it can detect this feature anywhere in the image, making CNNs inherently translation invariant.
With fewer parameters to learn, CNNs are less likely to overfit the training data. This improves the model’s ability to generalize from the training data to unseen data, enhancing its performance on real-world tasks.
How Weight Sharing Works
During the forward pass, a filter with a fixed set of weights slides over the input image, computing the dot product between the filter weights and the local regions of the image. This process generates a feature map that indicates the presence and intensity of the detected feature across the spatial extent of the image.
Despite the extensive reuse of weights across the spatial domain, each weight is updated based on the aggregate gradient from all positions where it was applied. This ensures that the filter weights are optimized to detect features that are most relevant for the task, based on the entire dataset.
2.6: Feature Map Creation
As we saw previously, a feature map is an output generated by applying a filter or kernel to the input image or a preceding feature map within a CNN. It represents the responses of the filter across the spatial dimensions of the input, highlighting where and how specific features are detected in the image. Let’s now recap how each element in the CNN affects the resulting feature map.
At the core of feature map creation is the convolution operation, where a filter with learned weights slides (or convolves) across the input image or feature map from a previous layer. At each position, the filter performs an element-wise multiplication with the part of the image it covers, and the results are summed up to produce a single output pixel in the new feature map.
The weights in the filter determine the type of feature it detects, such as edges, textures, or more complex patterns in deeper layers. During training, these weights are adjusted through backpropagation, allowing the network to learn which features are most important for the task at hand.
The size of the stride and the use of padding directly affect the spatial dimensions of the feature map. A larger stride results in broader coverage with less overlap between filter applications, reducing the feature map size. Padding can be used to preserve the spatial dimensions of the input, ensuring that features at the edges of the image are not lost.
A convolutional layer typically contains multiple filters, each designed to detect different features. The output for each filter is a separate feature map, and these are stacked along the depth dimension to create a 3D volume. This multi-faceted approach allows the network to capture a rich representation of the input image.
After a feature map is created through the convolution operation, it is often passed through an activation function, such as ReLU. This introduces non-linearity, enabling the network to learn and represent more complex patterns.
If you want to learn more about ReLU and other activation functions, take a look at this article:
The Math Behind Neural Networks
The activated feature map then proceeds to the next layer or a pooling operation.
2.7: Pooling Layers
Pooling layers serve to reduce the spatial dimensions of the feature maps. This reduction is crucial for decreasing the computational load, minimizing overfitting, and retaining only the most essential information. Let’s delve into the specifics of pooling layers, their types, and their impact on CNN performance.
Pooling layers reduce the size of the feature maps, thereby decreasing the number of parameters and computations required in the network. This simplification helps to focus on the most important features.
By summarizing the presence of features in patches of the feature map, pooling helps the network to maintain robustness to minor variations and translations in the input image.
There are a few types of pooling techniques you should know about when playing with CNNs:
Max Pooling
This is the most common form of pooling, where the maximum value from a set of values in the feature map is selected and forwarded to the next layer. Max pooling effectively captures the most pronounced feature in each patch of the feature map.
We denote the feature map by F and the pooling operation by P_max, the result of max pooling at position (i,j) for a window size of n×n can be expressed as:

Here, s is the stride of the pooling window, and a, b iterate over the window dimensions. This operation is applied independently for each window position across the feature map.
Average Pooling
Unlike max pooling, average pooling takes the average of the values in each patch of the feature map. This method provides a more generalized feature representation but might dilute the presence of smaller, yet significant features.
For a feature map F and an n×n pooling window, the average pooling operation at position (i,j) can be mathematically represented as:

Similar to max pooling, s represents the stride, and a,b iterate over the window, but here the operation computes the mean of the values within each window.
Global Pooling
In global pooling, the entire feature map is reduced to a single value by taking the max (global max pooling) or average (global average pooling) of all values in the feature map. This approach is often used to reduce each feature map to a single value before a fully connected layer.
For a feature map F of size M×N, global max pooling (P_gmax) and global average pooling (P_gavg) can be defined as:

Global pooling operations compress the entire feature map into a single summary statistic, which is particularly useful for reducing model parameters before a fully connected layer for classification.
How Pooling Works
A pooling layer operates over each feature map independently, sliding a window (or filter) across the feature map and summarizing the values within that window into a single value (based on the pooling strategy used). This process reduces the spatial dimensions of the feature map.
The size of the window and the stride (how far the window moves each time) determine how much the feature map is reduced. A common choice is a 2×2 window with a stride of 2, which reduces the size of the feature map by half.
2.8: Fully Connected Layers

Fully connected layers are often positioned towards the end of CNNs. These layers are where the high-level reasoning based on the learned features takes place, ultimately leading to classification or prediction.
In a fully connected layer, every neuron is connected to every activation from the previous layer. This dense connectivity ensures that the layer has the complete context of the extracted features, allowing it to learn complex patterns that are distributed across the feature map.
Fully connected layers integrate the spatially distributed features identified by convolutional and pooling layers into a global representation of the input. This integration is crucial for tasks I Hthat require an understanding of the entire input, such as classification.
From Convolutional to Fully Connected Layers
Before entering a fully connected layer, the output from the preceding convolutional or pooling layers, typically a multi-dimensional feature map, is flattened into a single vector. This step transforms the spatially structured data into a format suitable for processing by fully connected layers.
The neurons in fully connected layers can learn high-level patterns in the data by considering the global information presented by the flattened feature map. This ability is fundamental to making predictions or classifications based on the entire input image.
Role in CNNs
In many CNN architectures, the final fully connected layer serves as the classification layer, where each neuron represents a specific class. The network’s prediction is determined by the activation of these neurons, typically through a softmax function that converts the activations into probabilities.
Fully connected layers synthesize the localized, abstract features extracted by the convolutional layers into a cohesive understanding of the input data. This synthesis is essential for the network to reason about the input as a whole and make informed decisions.
3: Step-by-Step Guide to Building a CNN
Let’s get into business and build our CNN. We will set up, train, and evaluate a Convolutional Neural Network (CNN) using PyTorch for image classification on the MNIST dataset, an open-source large database of handwritten digits. [MNIST dataset is made available under the terms of the Creative Commons Attribution-Share Alike 3.0 license]
Feel free to have this Jupyter Notebook on the side, which contains all the code we will cover today:
3.1: Setting Up the Environment
Let’s start with the necessary libraries and modules. PyTorch (torch), its neural network module (nn), and optimization module (optim) are imported for constructing and training the neural network. Functionalities from torch.nn.functional are used for operations like ReLU activation and max pooling. DataLoader utilities facilitate batch processing and data management, and torchvision is used for handling datasets and image transformations.
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn, optim
from torch.nn import functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
3.2: Preparing the Data
The MNIST dataset is loaded with a transformation pipeline that first converts images to tensor format, and then normalizes their pixel values. Normalization parameters (mean=0.1307, std=0.3081) are chosen specifically for the MNIST dataset to standardize its grayscale images for optimal neural network performance.
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
mnist_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
A sample image from the dataset is displayed using matplotlib, illustrating the type of data the network will be trained on.
image, label = mnist_dataset[0]
plt.imshow(image.squeeze().numpy(), cmap='gray')
plt.title(f'Label: {label}')
plt.show()
This code will show the following image:

The dataset is divided into training and validation sets to enable model evaluation during training. DataLoader instances handle batching, shuffling, and preparing the dataset for efficient processing by the neural network.
train_size = int(0.8 * len(mnist_dataset))
val_size = len(mnist_dataset) - train_size
train_dataset, val_dataset = random_split(mnist_dataset, [train_size, val_size])
3.3: Designing the CNN Model
Once we preprocessed data, we can proceed to the model creation. Therefore, we initialize a MyCNN class, which inherits from nn.Module, which is PyTorch’s way of defining a model. This inheritance gives MyCNN all the functionalities of a PyTorch model, including the ability to train, make predictions, and more.
The __init__ function is the constructor of the MyCNN class. It’s where the layers of the neural network are defined. The super(MyCNN, self).__init__() line calls the constructor of the base nn.Module class, which is necessary for PyTorch to initialize everything correctly.
class MyCNN(nn.Module):
def __init__(self):
super(MyCNN, self).__init__()
self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
self.fc1 = nn.Linear(7*7*64, 128)
self.fc2 = nn.Linear(128, 10)
As you can notice from the code above, the network includes two convolutional layers, conv1 and conv2.
conv1 takes a single-channel image (like a grayscale image) as input and produces 32 feature maps using a filter (or kernel) size of 3×3, with a stride of 1 and padding of 1. Padding is added to ensure the output feature maps are the same size as the input.
conv2 takes the 32 feature maps from conv1 as input and produces 64 feature maps, also with a 3×3 kernel, stride of 1, and padding of 1. This layer further extracts features from the input provided by conv1.
After the convolutional layers, there are two fully connected (fc) layers.
fc1 is the first fully connected layer that transforms the output from the convolutional layers into a vector of size 128. The input size is 7*7*64, which implies that before reaching this layer, the feature maps are flattened into a single vector and that the dimensionality of the feature maps before flattening is 7×7 with 64 channels. This step is crucial for transitioning from spatial feature extraction to making decisions (classifications) based on those features.
fc2 is the second fully connected layer, which takes the 128-dimensional vector from fc1 and outputs a 10-dimensional vector. This output size typically corresponds to the number of classes in a classification problem, suggesting this network is designed to classify images into one of 10 categories.
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.normal_(m.weight, 0, 0.01)
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.xavier_uniform_(m.weight)
if m.bias is not None:
nn.init.constant_(m.bias, 0)
Weight initialization is applied to ensure the network starts with weights in a range that neither vanishes nor explodes the gradients. Convolutional layers are initialized with normal distribution, while fully connected layers use Xavier uniform initialization.
To learn more about Xavier initialization and other types of initialization consider diving into my previous article:
The Math Behind Fine-Tuning Deep Neural Networks
The forward method within the MyCNN class defines the sequence of operations that input data undergoes as it passes through the CNN.
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
Let’s dissect this method step by step, focusing on each operation to understand how input images are transformed into output predictions.
First Convolutional Layer
x = F.relu(self.conv1(x))
The input tensor x, representing the batch of images, is passed through the first convolutional layer (conv1). This layer applies learned filters to the input, capturing basic visual features like edges and textures. The convolution operation is immediately followed by a ReLU activation function applied in-place. ReLU sets all negative values in the output tensor to zero, enhancing the network’s ability to distinguish features.
First Pooling Operation
x = F.max_pool2d(x, 2, 2)
Following the first convolution and activation, a max pooling operation is applied. This operation reduces the spatial dimensions of the feature map by half (due to the pool size and stride of 2), summarizing the most significant features within 2×2 patches of the feature map. Max pooling helps to make the representation somewhat invariant to small shifts and distortions.
Second Convolutional Layer
x = F.relu(self.conv2(x))
The process repeats with a second convolutional layer (conv2), which applies another set of learned filters to the now-reduced feature map. This layer typically captures more complex features, building upon the basic patterns identified by the first layer. Again, ReLU activation follows to maintain non-linearity in the learning process.
Second Pooling Operation
x = F.max_pool2d(x, 2, 2)
Another max pooling step further reduces the spatial dimensions of the resulting feature map, compacting the feature representation and reducing computational complexity for subsequent layers.
Flattening
x = x.view(x.size(0), -1)
Before transitioning to fully connected layers, the multidimensional feature map must be flattened into a single vector per image in the batch. This operation reshapes the tensor so that each image’s feature map becomes a single row in the tensor, preserving all feature information in a format suitable for fully connected processing.
First Fully Connected Layer
x = F.relu(self.fc1(x))
The flattened tensor is passed through the first fully connected layer (fc1), where neurons can learn complex patterns from the entire feature set. The ReLU function is applied once more to introduce non-linearity, enabling the network to learn and represent more complex functions.
Second Fully Connected Layer (Output Layer)
x = self.fc2(x)
Finally, the tensor passes through a second fully connected layer (fc2), which acts as the output layer. This layer has as many neurons as there are classes to predict (10 for MNIST digits). The output of this layer represents the network’s predictions for each class.
3.4: Compiling the Model
The model is compiled with CrossEntropyLoss for classification and the Adam optimizer for adjusting weights, along with specific parameters like learning rate and weight decay.
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-5, amsgrad=True, eps=1e-8, betas=(0.9, 0.999))
The Adam optimizer is a popular algorithm for training deep learning models, combining the best properties of the AdaGrad and RMSProp algorithms to efficiently handle sparse gradients on noisy problems. It adjusts the learning rate on a per-parameter basis, making it highly effective and well-suited for a wide range of tasks and models. If you want to learn more about Adam take a look at my article where I go through its math and build it from scratch:
The Math behind Adam Optimizer
3.5: Training the CNN
The Trainer class in the provided logic necessary for training the CNN model, including the forward pass, and backward pass (gradient calculation and weight update), monitoring the training and validation losses, implementing early stopping, adjusting the learning rate, and evaluating the model’s performance. Let’s dissect this class to understand its structure and functionality in depth.
class Trainer:
def __init__(self, model, criterion, optimizer, device, patience=7):
self.model = model
self.criterion = criterion
self.optimizer = optimizer
self.device = device
self.early_stopping = EarlyStopping(patience=patience)
self.scheduler = ReduceLROnPlateau(self.optimizer, 'min', patience=3, verbose=True, factor=0.5, min_lr=1e-6)
self.train_losses = []
self.val_losses = []
self.gradient_norms = []
In the initialization method __init__, the Trainer class takes the CNN model, the loss function (criterion), and the optimizer as arguments, alongside the device on which to run the training (CPU or GPU) and the patience for early stopping. An EarlyStopping instance is created to monitor validation loss and halt training if the model ceases to improve, preventing overfitting. A learning rate scheduler (ReduceLROnPlateau) is also initialized to dynamically adjust the learning rate based on the validation loss, helping to find the optimal learning rate during training. Lists to track training and validation losses, as well as gradient norms, are initialized for analysis and debugging purposes.
def train(self, train_loader, val_loader, epochs):
for epoch in range(epochs):
self.model.train()
for images, labels in train_loader:
images, labels = images.to(self.device), labels.to(self.device)
self.optimizer.zero_grad()
outputs = self.model(images)
loss = self.criterion(outputs, labels)
self.train_losses.append(loss.item())
loss.backward()
self.optimizer.step()
The train method orchestrates the training process over a specified number of epochs. For each epoch, it sets the model to training mode and iterates over the training dataset using the train_loader. Input images and labels are moved to the specified device. The optimizer’s gradients are zeroed before each forward pass to prevent accumulation from previous iterations. The model’s predictions are obtained, and the loss is calculated using the specified criterion. The loss value is appended to the train_losses list for tracking. Backpropagation is performed by calling loss.backward(), and the optimizer updates the model weights with optimizer.step().
val_loss = self.evaluate(val_loader)
self.val_losses.append(val_loss)
self.scheduler.step(val_loss)
self.early_stopping(val_loss)
After processing the training data, the model is evaluated on the validation dataset using the evaluate method, which calculates the average validation loss. This loss is used to adjust the learning rate with the scheduler and to determine if early stopping conditions are met. Validation loss is tracked for analysis.
if self.early_stopping.early_stop:
print("Early stopping")
break
If early stopping is triggered, training is halted to prevent overfitting. This decision is based on whether the validation loss has stopped improving over several epochs defined by the patience parameter.
def evaluate(self, test_loader):
self.model.eval()
total_loss = 0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(self.device), labels.to(self.device)
outputs = self.model(images)
loss = self.criterion(outputs, labels)
total_loss += loss.item()
return total_loss / len(test_loader)
The evaluate method calculates the average loss over the validation or test dataset without updating the model’s weights. It sets the model to evaluation mode and disables gradient computations for efficiency.
4: Improving Model Performance
Improving the performance of Convolutional Neural Networks (CNNs) and preventing overfitting are critical challenges in training deep learning models. The code snippet provided does not explicitly detail techniques like data augmentation, dropout, and batch normalization, nor does it delve into transfer learning. However, these strategies are essential for enhancing CNNs, so let’s explore how they can be integrated into the training process and their potential impact on model performance.
4.1: Data Augmentation
Data augmentation artificially increases the diversity of the training dataset by applying random transformations (e.g., rotation, flipping, scaling) to the existing images. This diversity helps the model generalize better to new, unseen data by learning from a broader range of input variations.
To implement data augmentation in PyTorch, you can extend the transforms.Compose used in preparing the dataset:
transform = transforms.Compose([
transforms.RandomHorizontalFlip(),
transforms.RandomRotation(10),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
Adding random flips and rotations diversifies the training data, encouraging the model to learn more robust features.
4.2: Dropout
Dropout is a regularization technique that randomly sets a fraction of input units to 0 during training, preventing units from co-adapting too much. This randomness forces the network to learn more robust features that are useful in conjunction with various random subsets of the other neurons.
In PyTorch, dropout can be added to the CNN model by including nn.Dropout layers:
class MyCNN(nn.Module):
def __init__(self):
super(MyCNN, self).__init__()
# Convolutional layers
self.fc1 = nn.Linear(7*7*64, 128)
self.dropout = nn.Dropout(0.5)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
# Convolutional and pooling operations
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = self.dropout(x)
x = self.fc2(x)
return x
Adding a dropout layer before the final fully connected layer helps mitigate overfitting by encouraging the model to distribute the learned representation across multiple neurons.
4.3: Batch Normalization
Batch normalization standardizes the inputs to a layer for each mini-batch, stabilizing the learning process and significantly reducing the number of training epochs required to train deep networks.
Batch normalization can be incorporated into the model as follows:
class MyCNN(nn.Module):
def __init__(self):
super(MyCNN, self).__init__()
# Convolutional layers
self.conv1_bn = nn.BatchNorm2d(32)
# Fully connected layers
def forward(self, x):
x = F.relu(self.conv1_bn(self.conv1(x)))
# Continue through model
Applying batch normalization after convolutional layers but before the activation function helps in normalizing the output, contributing to faster convergence and improved overall performance.
4.4: Transfer Learning
Transfer learning involves using a model trained on one task as the starting point for training on a different but related task. This technique is particularly useful when you have a limited dataset for the new task. PyTorch facilitates transfer learning by allowing models pre-trained on large datasets (like ImageNet) to be easily loaded and adapted.
To leverage a pre-trained model in PyTorch:
from torchvision import models
model = models.resnet18(pretrained=True)
# Replace the final fully connected layer
num_ftrs = model.fc.in_features
model.fc = nn.Linear(num_ftrs, 10) # Assuming 10 classes for the new task
# Freeze all layers but the last fully connected layer
for param in model.parameters():
param.requires_grad = False
model.fc.requires_grad = True
Here, a pre-trained ResNet-18 model is adapted for a new task with 10 classes by replacing its final layer. Freezing the weights of all layers except the last one allows us to fine-tune only the classifier layer, leveraging the feature extraction capabilities learned from the original dataset.
Incorporating these strategies into the CNN training process not only combats overfitting but also enhances model performance by ensuring robust feature learning and leveraging knowledge from pre-trained models.
5: Conclusion
Wrapping up our deep dive into Convolutional Neural Networks, we’ve covered a lot. From setting up and preparing data to dissecting CNN architecture and its layers, we’ve seen what makes these models tick. We’ve looked into how tweaking things like weight initialization and using techniques like data augmentation and transfer learning can seriously boost a model’s performance. These methods help make our models smarter, avoiding common pitfalls like overfitting and making them more versatile.
CNNs are pretty much everywhere in AI now, helping with everything from spotting faces in photos to diagnosing diseases from medical images. Their knack for picking up on visual cues makes them super valuable for a whole range of tasks.
Additional Resources
- LeCun et al., “Gradient-Based Learning Applied to Document Recognition”
This seminal paper by Yann LeCun and colleagues introduces LeNet-5, one of the first convolutional neural networks, and demonstrates its application to document recognition tasks.
Research Gate Link - Simonyan and Zisserman, “Very Deep Convolutional Networks for Large-Scale Image Recognition” (VGGNet)
This work introduces VGGNet, highlighting the importance of depth in CNN architectures for improving image recognition performance.
arXiv Link - He et al., “Deep Residual Learning for Image Recognition” (ResNet)
ResNet introduces the concept of residual learning, enabling the training of much deeper networks by addressing the vanishing gradient problem.
arXiv Link
If you liked this article consider leaving a like, and follow me to be updated on my latest posts. My goal is to recreate all the most popular algorithms from scratch and make machine learning accessible to everyone.
The Math Behind Convolutional Neural Networks was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The Math Behind Convolutional Neural Networks
Go Here to Read this Fast! The Math Behind Convolutional Neural Networks