
Originally appeared here:
Transform customer engagement with no-code LLM fine-tuning using Amazon SageMaker Canvas and SageMaker JumpStart


Originally appeared here:
Transform customer engagement with no-code LLM fine-tuning using Amazon SageMaker Canvas and SageMaker JumpStart



Readers of my prior work may remember when I covered “Textbooks are all you need”, a paper by Microsoft showing how quality data can have an outsize impact on model performance. The findings there directly refuted the belief that models had to be enormous to be capable. The researchers behind that paper have continued their work and published something I find incredibly exciting.
The title of this paper explains perhaps the biggest finding: “Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone”.
Let’s dive into what the authors changed from the Phi-2 model, how they trained it, and how it works on your iPhone.
There are a few key concepts to know before we dive into the architecture. If you know these already, feel free to skip to the next section.
A model’s parameters refer to the number of weights and biases that the model learns during training. If you have 1 billion parameters, then you have 1 billion weights and biases that determine the model’s performance. The more parameters you have the more complex your neural network can be. A head refers to the number of key, value, and query vectors the self-attention mechanism in a Transformer has. Layers refers to the number of neural segments that exist within the neural network of the Transformer, with hidden dimensions being the number of neurons within a typical hidden layer.
Tokenizer is the software piece that will convert your input text into an embedding that the transformer will then work with. Vocabulary size refers to the number of unique tokens that the model is trained on. The block structure of a transformer is how we refer to the combination of layers, heads, activation functions, tokenizer and layer normalizations that would be chosen for a specific model.

Grouped-Query Attention (GQA) is a way that we optimize multi-head attention to reduce the computational overhead during training and inference. As you can see from the image below, GQA takes the middle-ground approach — rather than pairing 1 value and 1 key to 1 query, we take a 1:1:M approach, with the many being smaller than the entire body of queries. This is done to still get the training cost benefits from Multi-Query Attention (MQA), while minimizing the performance degradation that we see follow that.
Let’s begin with the architecture behind this model. The researchers released 3 different decoder only models, phi-3-mini, phi-3-small, and phi-3-medium, with different hyperparameters for each.
Going into some of the differences here, the phi-3-mini model was trained using typical mutli-head attention. While not called out in the paper, my suspicion is that because the model is roughly half the size of the other two, the training costs associated with multi-head were not objectionable. Naturally when they scaled up for phi-3-small, they went with grouped query attention, with 4 queries connected to 1 key.
Moreover, they kept phi-3-mini’s block structure as close to the LLaMa-2 structure as they could. The goal here was to allow the open-source community to continue their research on LLaMa-2 with Phi-3. This makes sense as a way to further understand the power of that block structure.
However, phi-3-small did NOT use LLaMa’s block structure, opting to use the tiktoken tokenizer, with alternate layers of dense attention and a new blocksparse attention. Additionally, they added in 10% multilingual data to the training dataset for these models.
Similar to Phi-2, the researchers invested majorly in quality data. They used the similar “educational value” paradigm they had used before when generating data to train the model on, opting to use significantly more data than last time. They created their data in 2 phases.
Phase-1 involved finding web data that they found was of high “educational value” to the user. The goal here is to give general knowledge to the model. Phase-2 then takes a subset of the Phase-1 data and generates data that would teach the model how to logically reason or attain specific skills.
The challenge here was to ensure the mix of data from each corpus was appropriate for the scale of the model being trained (ie phi-3-small vs phi-3-mini). This is the idea behind a “data optimal” regime, where the data you are giving to the LLM to train with gives it the best ability for its block structure. Put differently, if you think that data is a key distinguisher for training a good LLM, then finding the right combination of skills to show the model via your data can be just as key as finding good data. The researchers highlighted that they wanted the model to have stronger reasoning than knowledge abilities, resulting in their choosing more data from the Phase-2 corpus than from the Phase-1.
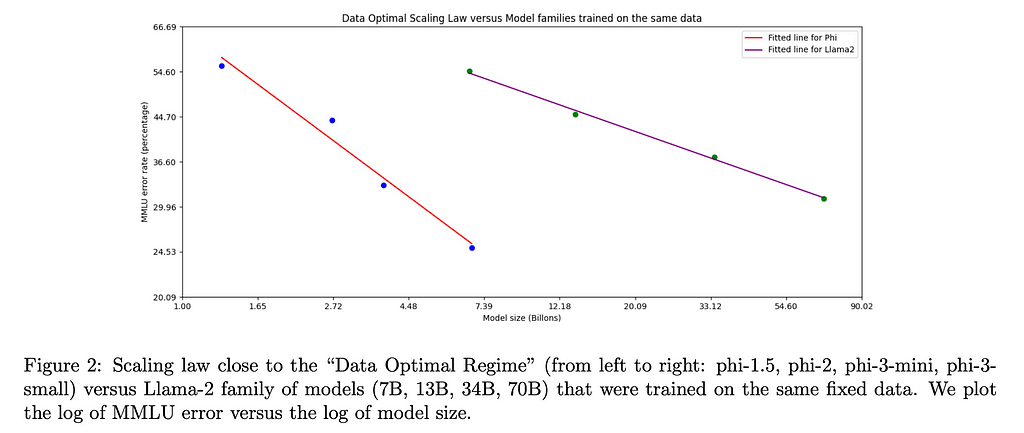
Interestingly, when they were training phi-3-medium with roughly the same data mixture as they trained phi-3-small, they noticed that the improvements from 7B parameters to 14B were far more limited than from 3.8B to 7B. The authors suspect this is not a limitation of the block structure, but instead of the data mixture they used to train phi-3-medium.
The team used both Supervised Fine Tuning (SFT) and Direct Preference Optimization (DPO) to improve the model post-training. Those interested in a deep dive on DPO can check out my blog post here. Supervised Fine Tuning is a type of transfer learning where we use a custom dataset to improve the LLM’s capabilities on that dataset. The authors used SFT to improve the model’s ability across diverse domains like math, coding, reasoning, and safety. They then used DPO for their chat optimization to guide it away from responses they wanted to avoid and towards ideal responses.
It’s in this stage that the authors expanded the context window of phi-3-mini from 4k tokens to 128k tokens. The methodology they used to do this is called Long Rope. The authors claim that the performance is consistent between the 2 context types, which is a big deal given the enormous increase in context length. If there is sufficient interest, I will do a separate blog post on the findings within that paper.
Even though these models are small, to get these models to run on your phone still requires some further minimization. Typically the weights for a LLM is stored as float; for example, Phi-3’s original weights were bfloat16, meaning each weight takes up 16 bits in memory. While 16 bits may seem trivial, when you take into account there are on the order of 10⁹ parameters in the model, you realize how quickly each additional bit adds up.
To get around this, the authors condensed the weights from 16 bits to 4 bits. The basic idea is to reduce the number of bits required to store each number. For a conceptual example, the number 2.71828 could be condensed to 2.72. While this is a lossy operation, it still captures a good portion of the information while taking significantly less storage.

The authors ran the quantized piece on an iPhone with the A16 chip and found it could generate up to 12 tokens per second. For comparison, an M1 MacBook running LLaMa-2 Quantized 4 bit runs at roughly 107 tokens per second. The fastest token generation I’ve seen (Groq) generated tokens at a rate of 853.35 Tokens per second. Given this is just the beginning, it’s remarkable how fast we are able to see tokens generated on an iPhone with this model. It seems likely the speed of inference will only increase.
One limitation with a small model is it has fewer places it can store information within its network. As a result, we see that Phi-3 does not perform as well as models like LLaMa-2 on tasks that require wide scopes of knowledge.
The authors suggest that by pairing Phi-3 with a search engine the model’s abilities will significantly improve. If this is the case, that makes me think Retrieval Augmented Generation (RAG) is likely here to stay, becoming a critical part of helping small models be just as performant as larger ones.

In closing, we are seeing the beginning of highly performant smaller models. While training these models still relies to a large degree on performant hardware, inferencing them is increasingly becoming democratized. This introduces a few interesting phenomena.
First, models that can run locally can be almost fully private, allowing users to give these LLMs data that they otherwise may not feel comfortable sending over the internet. This opens the door to more use cases.
Second, these models will drive mobile hardware to be even more performant. As a consequence, I would expect to see more Systems on Chips (SoC) on high-end smartphones, especially SoCs with shared memory between CPUs and GPUs to maximize the speed of inference. Moreover, the importance of having quality interfaces with this hardware will be paramount. Libraries like MLX for Apple Silicon will likely be required for any new hardware entrants in the consumer hardware space.
Third, as this paper shows that high quality data can in many ways outcompete more network complexity in an LLM, the race to not just find but generate high quality data will only increase.
It is an exciting time to be building.
[1] Abdin, M., et al. “Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone” (2024), arXiv
[2] Ding, Y., et al. “LongRoPE: Extending LLM Context Window Beyond 2 Million Tokens” (2024), arXiv
[3] Gerganov, G., et al. “Performance of llama.cpp on Apple Silicon M-series” (2023), GitHub
[4] Ainslie, J., et al. “GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints” (2023), arXiv
Phi-3 and the Beginning of Highly Performant iPhone Models was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Phi-3 and the Beginning of Highly Performant iPhone Models
Go Here to Read this Fast! Phi-3 and the Beginning of Highly Performant iPhone Models

Feature selection is a critical step in many machine learning pipelines. In practice, we generally have a wide range of variables available as predictors for our models, but only a few of them are related to our target. Feature selection consists of finding a reduced set of these features, mainly for:
There are many techniques available to perform feature selection, each with varying complexity. In this article, I want to share a way of using a powerful open source optimization tool, Optuna, to perform the feature selection task in an innovative way. The main idea is to have a flexible tool that can handle feature selection for a wide range of tasks, by efficiently testing different feature combinations (e.g., not trying them all one by one). Below, we’ll go through a hands-on example implementing this approach, and also comparing it to other common feature selection strategies. To experiment with the feature selection techniques discussed, you can follow along with this Colab Notebook.
In this example, we’ll focus on a classification task based on the Mobile Price Classification dataset from Kaggle. We have 20 features, including ‘battery_power’, ‘clock_speed’ and ‘ram’, to predict the ‘price_range’ feature, which can belong to four different bands: 0, 1, 2 and 3.
We first split our dataset into train and test sets, and we also prepare a 5-fold validation split within the train set — this will be useful later on.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
SEED = 32
# Load data
filename = "train.csv" # train.csv from https://www.kaggle.com/datasets/iabhishekofficial/mobile-price-classification
df = pd.read_csv(filename)
# Train - test split
df_train, df_test = train_test_split(df, test_size=0.2, stratify=df.iloc[:,-1], random_state=SEED)
df_train = df_train.reset_index(drop=True)
df_test = df_test.reset_index(drop=True)
# The last column is the target variable
X_train = df_train.iloc[:,0:20]
y_train = df_train.iloc[:,-1]
X_test = df_test.iloc[:,0:20]
y_test = df_test.iloc[:,-1]
# Stratified kfold over the train set for cross validation
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=SEED)
splits = list(skf.split(X_train, y_train))
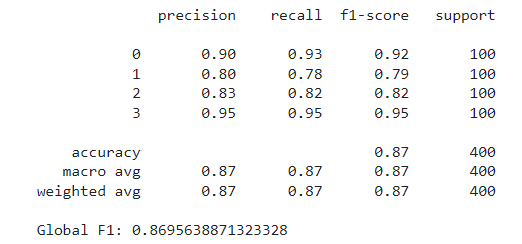
The model we’ll use throughout the example is the Random Forest Classifier, using the scikit-learn implementation and default parameters. We first train the model using all features to set our benchmark. The metric we’ll measure is the F1 score weighted for all four price ranges. After fitting the model over the train set, we evaluate it on the test set, obtaining an F1 score of around 0.87.
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import f1_score, classification_report
model = RandomForestClassifier(random_state=SEED)
model.fit(X_train,y_train)
preds = model.predict(X_test)
print(classification_report(y_test, preds))
print(f"Global F1: {f1_score(y_test, preds, average='weighted')}")
The goal now is to improve these metrics by selecting a reduced feature set. We will first outline how our Optuna-based approach works, and then test and compare it with other common feature selection strategies.
Optuna is an optimization framework mainly used for hyperparameter tuning. One of the key features of the framework is its use of Bayesian optimization techniques to search the parameter space. The main idea is that Optuna tries different combinations of parameters and evaluates how the objective function changes with each configuration. From these trials, it builds a probabilistic model used to estimate which parameter values are likely to yield better outcomes.
This strategy is much more efficient compared to grid or random search. For example, if we had n features, and attempted to try each possible feature subset, we would have to perform 2^n trials. With 20 features these would be more than a million trials. Instead, with Optuna, we can explore the search space with much fewer trials.
Optuna offers various samplers to try. For our case, we’ll use the default one, the TPESampler, based on the Tree-structured Parzen Estimator algorithm (TPE). This sampler is the most commonly used, and it’s recommended for searching categorical parameters, which is our case as we’ll see below. According to the documentation, this algorithm “fits one Gaussian Mixture Model (GMM) l(x) to the set of parameter values associated with the best objective values, and another GMM g(x) to the remaining parameter values. It chooses the parameter value x that maximizes the ratio l(x)/g(x).”
As mentioned earlier, Optuna is typically used for hyperparameter tuning. This is usually done by training the model repeatedly on the same data using a fixed set of features, and in each trial testing a new set of hyperparameters determined by the sampler. The parameter set that minimizes the given objective function is then returned as the best trial.
In our case, however, we’ll use a fixed model with predetermined parameters, and in each trial, we’ll allow Optuna to select which features to try. The process aims to find the set of features that minimizes the loss function. In our case, we’ll guide the algorithm to maximize the F1 score (or minimize the negative of the F1). Additionally, we’ll add a small penalty for each feature used, to encourage smaller feature sets (if two feature sets yield similar results, we’ll prefer the one with fewer features).
The data we’ll use is the train dataset, split into five folds. In each trial, we’ll fit the classifier five times using four of the five folds for training and the remaining fold for validation. We’ll then average the validation metrics and add the penalty term to calculate the trial’s loss.
Below is the implemented class to perform the feature selection search:
import optuna
class FeatureSelectionOptuna:
"""
This class implements feature selection using Optuna optimization framework.
Parameters:
- model (object): The predictive model to evaluate; this should be any object that implements fit() and predict() methods.
- loss_fn (function): The loss function to use for evaluating the model performance. This function should take the true labels and the
predictions as inputs and return a loss value.
- features (list of str): A list containing the names of all possible features that can be selected for the model.
- X (DataFrame): The complete set of feature data (pandas DataFrame) from which subsets will be selected for training the model.
- y (Series): The target variable associated with the X data (pandas Series).
- splits (list of tuples): A list of tuples where each tuple contains two elements, the train indices and the validation indices.
- penalty (float, optional): A factor used to penalize the objective function based on the number of features used.
"""
def __init__(self,
model,
loss_fn,
features,
X,
y,
splits,
penalty=0):
self.model = model
self.loss_fn = loss_fn
self.features = features
self.X = X
self.y = y
self.splits = splits
self.penalty = penalty
def __call__(self,
trial: optuna.trial.Trial):
# Select True / False for each feature
selected_features = [trial.suggest_categorical(name, [True, False]) for name in self.features]
# List with names of selected features
selected_feature_names = [name for name, selected in zip(self.features, selected_features) if selected]
# Optional: adds a penalty for the amount of features used
n_used = len(selected_feature_names)
total_penalty = n_used * self.penalty
loss = 0
for split in self.splits:
train_idx = split[0]
valid_idx = split[1]
X_train = self.X.iloc[train_idx].copy()
y_train = self.y.iloc[train_idx].copy()
X_valid = self.X.iloc[valid_idx].copy()
y_valid = self.y.iloc[valid_idx].copy()
X_train_selected = X_train[selected_feature_names].copy()
X_valid_selected = X_valid[selected_feature_names].copy()
# Train model, get predictions and accumulate loss
self.model.fit(X_train_selected, y_train)
pred = self.model.predict(X_valid_selected)
loss += self.loss_fn(y_valid, pred)
# Take the average loss across all splits
loss /= len(self.splits)
# Add the penalty to the loss
loss += total_penalty
return loss
The key part is where we define which features to use. We treat each feature as one parameter, which can take the values True or False. These values indicate whether the feature should be included in the model. We use the suggest_categorical method so that Optuna selects one of the two possible values for each feature.
We now initialize our Optuna study and perform the search for 100 trials. Notice that we enqueue a first trial using all features, as a starting point for the search, allowing Optuna to compare subsequent trials against a fully-featured model:
from optuna.samplers import TPESampler
def loss_fn(y_true, y_pred):
"""
Returns the negative F1 score, to be treated as a loss function.
"""
res = -f1_score(y_true, y_pred, average='weighted')
return res
features = list(X_train.columns)
model = RandomForestClassifier(random_state=SEED)
sampler = TPESampler(seed = SEED)
study = optuna.create_study(direction="minimize",sampler=sampler)
# We first try the model using all features
default_features = {ft: True for ft in features}
study.enqueue_trial(default_features)
study.optimize(FeatureSelectionOptuna(
model=model,
loss_fn=loss_fn,
features=features,
X=X_train,
y=y_train,
splits=splits,
penalty = 1e-4,
), n_trials=100)
After completing the 100 trials, we retrieve the best one from the study and the features used in it. These are the following:
[‘battery_power’, ‘blue’, ‘dual_sim’, ‘fc’, ‘mobile_wt’, ‘px_height’, ‘px_width’, ‘ram’, ‘sc_w’]
Notice that from the original 20 features, the search concluded with only 9 of them, which is a significant reduction. These features yielded a minimum validation loss of around -0.9117, which means they achieved an average F1 score of around 0.9108 across all folds (after adjusting for the penalty term).
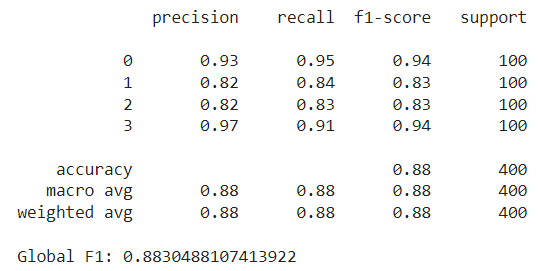
The next step is to train the model on the entire train set using these selected features and evaluate it on the test set. This results in an F1 score of around 0.882:
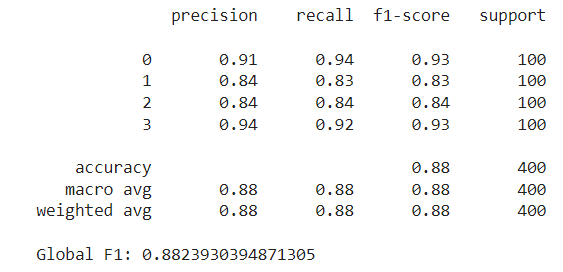
By selecting the right features, we were able to reduce our feature set by more than half, while still achieving a higher F1 score than with the full set. Below we will discuss some pros and cons of using Optuna for feature selection:
Pros:
Cons:
Next, we’ll compare our approach to other common feature selection strategies.
One of the simplest alternatives is to evaluate each feature individually using a statistial test and retain the top k features based on their scores. Notice that this approach doesn’t require any machine learning model. For example, for the classification task, we can choose the chi-squared test, which determines whether there is a statistically significant association between each feature and the target variable. We’ll use the SelectKBest class from scikit-learn, which applies the score function (chi-squared) to each feature and returns the top k scoring variables. Unlike the Optuna method, the number of features isn’t determined in the selection process, but must be set beforehand. In this case, we’ll set this number at ten. These methods fall within the filter methods class. They tend to be the easiest and fastest to compute since they don’t require any model behind.
from sklearn.feature_selection import SelectKBest, chi2
skb = SelectKBest(score_func=chi2, k=10)
skb.fit(X_train,y_train)
scores = pd.DataFrame(skb.scores_)
cols = pd.DataFrame(X_train.columns)
featureScores = pd.concat([cols,scores],axis=1)
featureScores.columns = ['feature','score']
featureScores.nlargest(10, 'score')
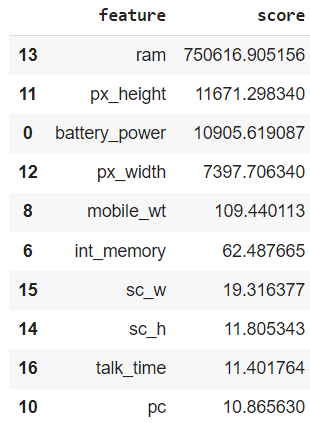
In our case, ram scored the highest by far in the chi-squared test, followed by px_height and battery_power. Notice that these features were also selected by our Optuna method above, along with px_width, mobile_wt and sc_w. However, there are some new additions like int_memory and talk_time — these weren’t picked by the Optuna study. After training the random forest with these 10 features and evaluating it on the test set, we achieved an F1 score slightly higher than our previous best, at approximately 0.888:
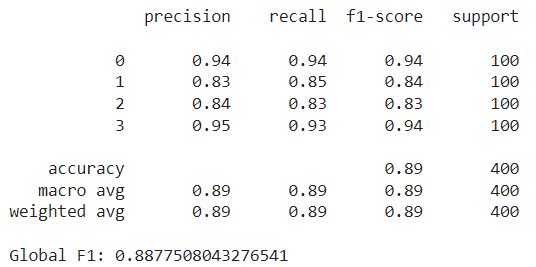
Pros:
Cons:
Wrapper methods are another class of feature selection strategies. These are iterative methods; they involve training the model with a set of features, evaluating its performance, and then deciding whether to add or remove features. Our Optuna strategy falls within these methods. However, most common examples include forward selection or backward selection. With forward selection, we begin with no features and, at each step, we greedily add the feature that provides the highest performance gain, until a stop criterion is met (number of features or performance decline). Conversely, backward selection starts with all features and iteratively removes the least significant ones at each step.
Below, we try the SequentialFeatureSelector class from scikit-learn, performing a forward selection until we find the top 10 features. This method will also make use of the 5-fold split we performed above, averaging performance across the validation splits at each step.
from sklearn.feature_selection import SequentialFeatureSelector
model = RandomForestClassifier(random_state=SEED)
sfs = SequentialFeatureSelector(model, n_features_to_select=10, cv=splits)
sfs.fit(X_train, y_train);
selected_features = list(X_train.columns[sfs.get_support()])
print(selected_features)
This method ends up selecting the following features:
[‘battery_power’, ‘blue’, ‘fc’, ‘mobile_wt’, ‘px_height’, ‘px_width’, ‘ram’, ‘talk_time’, ‘three_g’, ‘touch_screen’]
Again, some are common to the previous methods, and some are new (e.g., three_g and touch_screen. Using these features, the Random Forest achieves a lower test F1 score, slightly below 0.88.
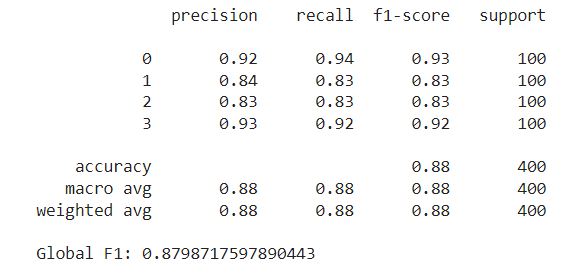
Pros
Cons
Finally, we’ll explore another straightforward selection strategy, which involves using the feature importances the model learns (if available). Certain models, like Random Forests, provide a measure of which features are most important for prediction. We can use these rankings to filter out those features that, according to the model, have the least importance. In this case, we train the model on the entire train dataset, and retain the 10 most important features:
model = RandomForestClassifier(random_state=SEED)
model.fit(X_train,y_train)
importance = pd.DataFrame({'feature':X_train.columns, 'importance':model.feature_importances_})
importance.nlargest(10, 'importance')
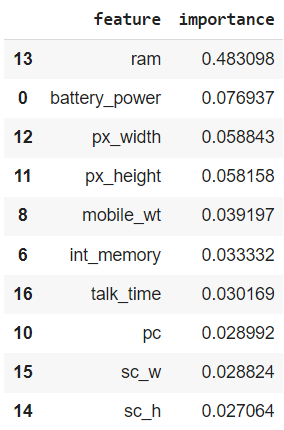
Notice how, once again, ram is ranked highest, far above the second most important feature. Training with these 10 features, we obtain a test F1 score of almost 0.883, similar to the ones we’ve been seeing. Also, note how the features selected through feature importance are the same as those selected using the chi-squared test, although they are ranked differently. This difference in ranking results in a slightly different outcome.
Pros:
Cons:
To conclude, we’ve seen how to use Optuna, a powerful optimization tool, for the feature selection task. By efficiently navigating the search space, it is able to find good feature subsets with relatively few trials. Not only that, but it is also flexible and can be adapted to many scenarios as long as we have a model and a loss function defined.
Throughout our examples, we observed that all techniques yielded similar feature sets and results. This is mainly because the dataset we used is rather simple. In these cases, simpler methods already produce a good feature selection, so it wouldn’t make much sense to go with the Optuna approach. However, for more complex datasets, with more features and intricate relationships between them, using Optuna might be a good idea. So, all in all, given its relative ease of implementation and ability to deliver good results, using Optuna for feature selection is a worthwhile addition to the data scientist’s toolkit.
Thanks for reading!
Colab Notebook: https://colab.research.google.com/drive/193Jwb0xXWh_UkvwIiFgufKEYer-86RNA?usp=sharing
Feature Selection with Optuna was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Feature Selection with Optuna
Feeling inspired to write your first TDS post? We’re always open to contributions from new authors.
Not so long ago, it seemed like landing your first data science job or switching to a more exciting data or ML role followed a fairly well-defined sequence. You learned new skills and expanded your existing ones, demonstrated your experience, zoomed in on the most fitting listings, and… sooner or later, something good would come your way.
Of course, things were never quite as straightforward, at least not for everyone. But even so, we’ve experienced somewhat of a mood shift in the past few months: the job market is more competitive, companies’ hiring processes more demanding, and there appears to be a lot more uncertainty and fluidity in tech and beyond.
What is an ambitious data professional to do? We prefer to avoid shortcuts and magic hacks in favor of foundational skills that showcase your deep understanding of the problems you aim to solve. Our most seasoned authors seem to point at the same direction: the lineup of articles we’re highlighting this week offer concrete insights for data and ML practitioners across a wide span of career stages and focus areas; they foreground continuous learning and building resilience in the face of change. Enjoy your reading!

There are so many different ways to grow as data and machine learning professionals; our other reading recommendations this week can each be its own point of departure for learning about new skills, tools, and workflows.
Thank you for supporting the work of our authors! We love publishing articles from new authors, so if you’ve recently written an interesting project walkthrough, tutorial, or theoretical reflection on any of our core topics, don’t hesitate to share it with us.
Until the next Variable,
TDS Team
How to Stand Out as a Data Scientist in 2024 was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
How to Stand Out as a Data Scientist in 2024
Go Here to Read this Fast! How to Stand Out as a Data Scientist in 2024
An intuitive visual explanation of the math behind logistic regression
Originally appeared here:
A Visual Understanding of Logistic Regression
Go Here to Read this Fast! A Visual Understanding of Logistic Regression