An outlier detector method that supports categorical data and provides explanations for the outliers flagged
Outlier detection is a common task in machine learning. Specifically, it’s a form of unsupervised machine learning: analyzing data where there are no labels. It’s the act of finding items in a dataset that are unusual relative to the others in the dataset.
There can be many reasons to wish to identify outliers in data. If the data being examined is accounting records and we’re interested in finding errors or fraud, there are usually far too many transactions in the data to examine each manually, and it’s necessary to select a small, manageable number of transactions to investigate. A good starting point can be to find the most unusual records and examine these; this is with the idea the errors and fraud should both be rare enough to stand out as outliers.
That is, not all outliers will be interesting, but errors and fraud will likely be outliers, so when looking for these, identifying the outliers can be a very practical technique.
Or, the data may contain credit card transactions, sensor readings, weather measurements, biological data, or logs from websites. In all cases, it can be useful to identify the records suggesting errors or other problems, as well as the most interesting records.
Often as well, outlier detection is used as part of business or scientific discovery, to better understand the data and the processes being described in the data. With scientific data, for example, we’re often interested in finding the most unusual records, as these may be the most scientifically interesting.
The need for interpretability in outlier detection
With classification and regression problems, it’s often preferable to use interpretable models. This can result in lower accuracy (with tabular data, the highest accuracy is usually found with boosted models, which are quite uninterpretable), but is also safer: we know how the models will handle unseen data. But, with classification and regression problems, it’s also common to not need to understand why individual predictions are made as they are. So long as the models are reasonably accurate, it may be sufficient to just let them make predictions.
With outlier detection, though, the need for interpretability is much higher. Where an outlier detector predicts a record is very unusual, if it’s not clear why this may be the case, we may not know how to handle the item, or even if we should believe it is anomalous.
In fact, in many situations, performing outlier detection can have limited value if there isn’t a good understanding of why the items flagged as outliers were flagged. If we are checking a dataset of credit card transactions and an outlier detection routine identifies a series of purchases that appear to be highly unusual, and therefore suspicious, we can only investigate these effectively if we know what is unusual about them. In some cases this may be obvious, or it may become clear after spending some time examining them, but it is much more effective and efficient if the nature of the anomalies is clear from when they are discovered.
As with classification and regression, in cases where interpretability is not possible, it is often possible to try to understand the predictions using what are called post-hoc (after-the-fact) explanations. These use XAI (Explainable AI) techniques such as feature importances, proxy models, ALE plots, and so on. These are also very useful and will also be covered in future articles. But, there is also a very strong benefit to having results that are clear in the first place.
In this article, we look specifically at tabular data, though will look at other modalities in later articles. There are a number of algorithms for outlier detection on tabular data commonly used today, including Isolation Forests, Local Outlier Factor (LOF), KNNs, One-Class SVMs, and quite a number of others. These often work very well, but unfortunately most do not provide explanations for the outliers found.
Most outlier detection methods are straightforward to understand at an algorithm level, but it is nevertheless difficult to determine why some records were scored highly by a detector and others were not. If we process a dataset of financial transactions with, for example, an Isolation Forest, we can see which are the most unusual records, but may be at a loss as to why, especially if the table has many features, if the outliers contain rare combinations of multiple features, or the outliers are cases where no features are highly unusual, but multiple features are moderately unusual.
Frequent Patterns Outlier Factor (FPOF)
We’ve now gone over, at least quickly, outlier detection and interpretability. The remainder of this article is an excerpt from my book Outlier Detection in Python (https://www.manning.com/books/outlier-detection-in-python), which covers FPOF specifically.
FPOF (FP-outlier: Frequent pattern based outlier detection) is one of a small handful of detectors that can provide some level of interpretability for outlier detection and deserves to be used in outlier detection more than it is.
It also has the appealing property of being designed to work with categorical, as opposed to numeric, data. Most real-world tabular data is mixed, containing both numeric and categorical columns. But, most detectors assume all columns are numeric, requiring all categorical columns to be numerically encoded (using one-hot, ordinal, or another encoding).
Where detectors, such as FPOF, assume the data is categorical, we have the opposite issue: all numeric features must be binned to be in a categorical format. Either is workable, but where the data is primarily categorical, it’s convenient to be able to use detectors such as FPOF.
And, there’s a benefit when working with outlier detection to have at our disposal both some numeric detectors and some categorical detectors. As there are, unfortunately, relatively few categorical detectors, FPOF is also useful in this regard, even where interpretability is not necessary.
The FPOF algorithm
FPOF works by identifying what are called Frequent Item Sets (FISs) in a table. These are either values in a single feature that are very common, or sets of values spanning several columns that frequently appear together.
Almost all tables contain a significant collection of FISs. FISs based on single values will occur so long as some values in a column are significantly more common than others, which is almost always the case. And FISs based on multiple columns will occur so long as there are associations between the columns: certain values (or ranges of numeric values) tend to be associated with other values (or, again, ranges of numeric values) in other columns.
FPOF is based on the idea that, so long as a dataset has many frequent item sets (which almost all do), then most rows will contain multiple frequent item sets and inlier (normal) records will contain significantly more frequent item sets than outlier rows. We can take advantage of this to identify outliers as rows that contain much fewer, and much less frequent, FISs than most rows.
Example with real-world data
For a real-world example of using FPOF, we look at the SpeedDating set from OpenML (https://www.openml.org/search?type=data&sort=nr_of_likes&status=active&id=40536, licensed under CC BY 4.0 DEED).
Executing FPOF begins with mining the dataset for the FISs. A number of libraries are available in Python to support this. For this example, we use mlxtend (https://rasbt.github.io/mlxtend/), a general-purpose library for machine learning. It provides several algorithms to identify frequent item sets; we use one here called apriori.
We first collect the data from OpenML. Normally we would use all categorical and (binned) numeric features, but for simplicity here, we will just use only a small number of features.
As indicated, FPOF does require binning the numeric features. Usually we’d simply use a small number (perhaps 5 to 20) equal-width bins for each numeric column. The pandas cut() method is convenient for this. This example is even a little simpler, as we just work with categorical columns.
from mlxtend.frequent_patterns import apriori
import pandas as pd
from sklearn.datasets import fetch_openml
import warnings
warnings.filterwarnings(action='ignore', category=DeprecationWarning)
data = fetch_openml('SpeedDating', version=1, parser='auto')
data_df = pd.DataFrame(data.data, columns=data.feature_names)
data_df = data_df[['d_pref_o_attractive', 'd_pref_o_sincere',
'd_pref_o_intelligence', 'd_pref_o_funny',
'd_pref_o_ambitious', 'd_pref_o_shared_interests']]
data_df = pd.get_dummies(data_df)
for col_name in data_df.columns:
data_df[col_name] = data_df[col_name].map({0: False, 1: True})
frequent_itemsets = apriori(data_df, min_support=0.3, use_colnames=True)
data_df['FPOF_Score'] = 0
for fis_idx in frequent_itemsets.index:
fis = frequent_itemsets.loc[fis_idx, 'itemsets']
support = frequent_itemsets.loc[fis_idx, 'support']
col_list = (list(fis))
cond = True
for col_name in col_list:
cond = cond & (data_df[col_name])
data_df.loc[data_df[cond].index, 'FPOF_Score'] += support
min_score = data_df['FPOF_Score'].min()
max_score = data_df['FPOF_Score'].max()
data_df['FPOF_Score'] = [(max_score - x) / (max_score - min_score)
for x in data_df['FPOF_Score']]
The apriori algorithm requires all features to be one-hot encoded. For this, we use panda’s get_dummies() method.
We then call the apriori method to determine the frequent item sets. Doing this, we need to specify the minimum support, which is the minimum fraction of rows in which the FIS appears. We don’t want this to be too high, or the records, even the strong inliers, will contain few FISs, making them hard to distinguish from outliers. And we don’t want this too low, or the FISs may not be meaningful, and outliers may contain as many FISs as inliers. With a low minimum support, apriori may also generate a very large number of FISs, making execution slower and interpretability lower. In this example, we use 0.3.
It’s also possible, and sometimes done, to set restrictions on the size of the FISs, requiring they relate to between some minimum and maximum number of columns, which may help narrow in on the form of outliers you’re most interested in.
The frequent item sets are then returned in a pandas dataframe with columns for the support and the list of column values (in the form of the one-hot encoded columns, which indicate both the original column and value).
To interpret the results, we can first view the frequent_itemsets, shown next. To include the length of each FIS we add:
frequent_itemsets['length'] =
frequent_itemsets['itemsets'].apply(lambda x: len(x))
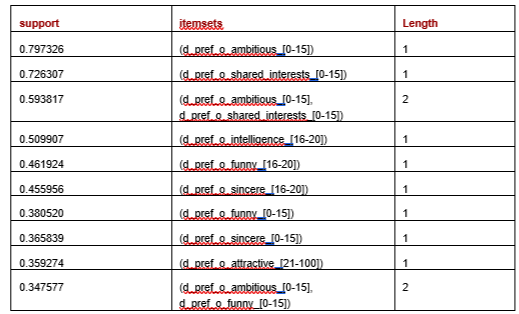
There are 24 FISs found, the longest covering three features. The following table shows the first ten rows, sorting by support.

We then loop through each frequent item set and increment the score for each row that contains the frequent item set by the support. This can optionally be adjusted to favor frequent item sets of greater lengths (with the idea that a FIS with a support of, say 0.4 and covering 5 columns is, everything else equal, more relevant than an FIS with support of 0.4 covering, say, 2 columns), but for here we simply use the number and support of the FISs in each row.
This actually produces a score for normality and not outlierness, so when we normalize the scores to be between 0.0 and 1.0, we reverse the order. The rows with the highest scores are now the strongest outliers: the rows with the least and the least common frequent item sets.
Adding the score column to the original dataframe and sorting by the score, we see the most normal row:

We can see the values for this row match the FISs well. The value for d_pref_o_attractive is [21–100], which is an FIS (with support 0.36); the values for d_pref_o_ambitious and d_pref_o_shared_interests are [0–15] and [0–15], which is also an FIS (support 0.59). The other values also tend to match FISs.
The most unusual row is shown next. This matches none of the identified FISs.

As the frequent item sets themselves are quite intelligible, this method has the advantage of producing reasonably interpretable results, though this is less true where many frequent item sets are used.
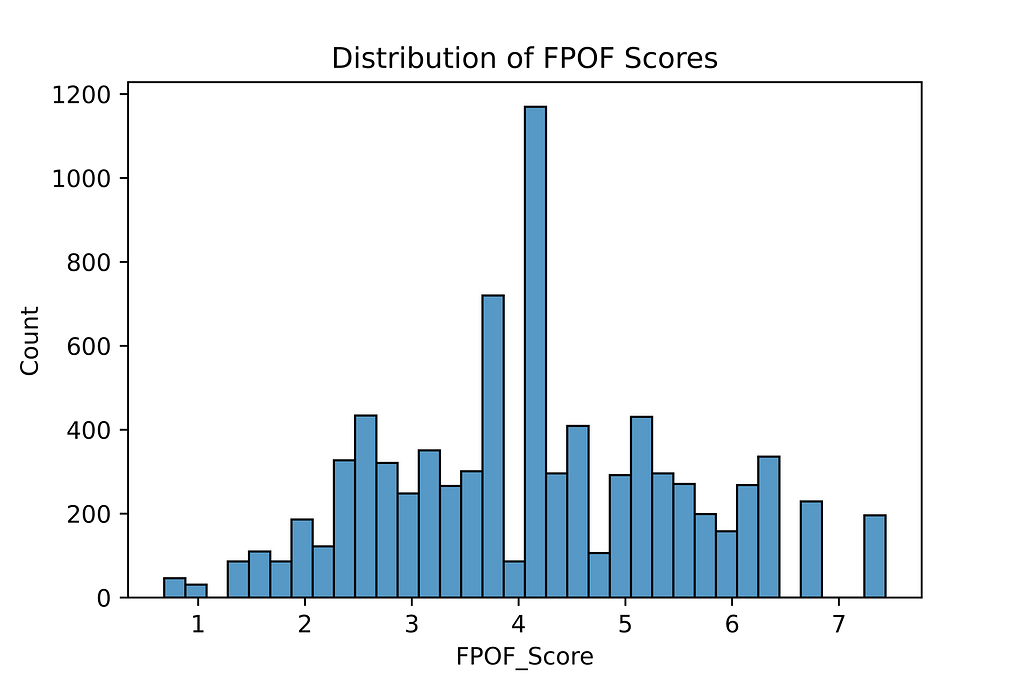
The interpretability can be reduced, as outliers are identified not by containing FISs, but by not, which means explaining a row’s score amounts to listing all the FISs it does not contain. However, it is not strictly necessary to list all missing FISs to explain each outlier; listing a small set of the most common FISs that are missing will be sufficient to explain outliers to a decent level for most purposes. Statistics about the the FISs that are present and the the normal numbers and frequencies of the FISs present in rows provides good context to compare.
One variation on this method uses the infrequent, as opposed to frequent, item sets, scoring each row by the number and rarity of each infrequent itemset they contain. This can produce useful results as well, but is significantly more computationally expensive, as many more item sets need to be mined, and each row is tested against many FISs. The final scores can be more interpretable, though, as they are based on the item sets found, not missing, in each row.
Conclusions
Other than the code here, I am not aware of an implementation of FPOF in python, though there are some in R. The bulk of the work with FPOF is in mining the FISs and there are numerous python tools for this, including the mlxtend library used here. The remaining code for FPOP, as seen above, is fairly simple.
Given the importance of interpretability in outlier detection, FPOF can very often be worth trying.
In future articles, we’ll go over some other interpretable methods for outlier detection as well.
All images are by author
Interpretable Outlier Detection: Frequent Patterns Outlier Factor (FPOF) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Interpretable Outlier Detection: Frequent Patterns Outlier Factor (FPOF)
Go Here to Read this Fast! Interpretable Outlier Detection: Frequent Patterns Outlier Factor (FPOF)