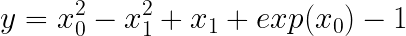Tag: AI

LLM Alignment: Reward-Based vs Reward-Free Methods

Optimization methods for LLM alignment

Context

Language models have demonstrated remarkable abilities in producing a wide range of compelling text based on prompts provided by users. However, defining what constitutes “good” text is challenging, as it often depends on personal preferences and the specific context. For instance, in storytelling, creativity is key; in crafting informative content, accuracy and reliability are crucial; and when generating code, ensuring it runs correctly is essential. Hence the “LLM alignment problem,” which refers to the challenge of ensuring that large language models (LLMs) act in ways that are consistent with human values, intentions, and preferences.

Designing a loss function that captures the diverse qualities we value in text — like creativity, accuracy, or executability — is highly complex and often impractical. Concepts like these are not differentiable and hence not back-propagated and cannot be trained upon with simple next token generation.

Imagine if we could harness human feedback to evaluate the quality of generated text or, even better, use that feedback as a guiding loss function to improve the model’s performance. This concept is at the heart of Reinforcement Learning from Human Feedback (RLHF). By applying reinforcement learning techniques, RLHF allows us to fine-tune language models based on direct human feedback, aligning the models more closely with nuanced human values and expectations. This approach has opened up new possibilities for training language models that are not only more responsive but also more aligned with the complexity of human preferences.

Below, we will aim to learn more about RLHF via reward-based and then about RLHF via reward-free methods.

What is Reinforcement learning through human feedback (RLHF) via a reward-based system?

Let’s go through Reinforcement learning through human feedback (RLHF). It consist of 3 main stages:

1. Supervised fine tuning
2. Reward modeling phase
3. RL fine-tuning phase

Supervised fine tuning

RLHF is a pre-trained model which is fine tuned already on a high quality data set. Its objective is simple i.e. when given an input (prompt), it produces an output. The ultimate objective here is to further fine tune this model to produce output according to human preference. Hence, let’s call this a base model for reference. Currently, this model is a vanilla base model which is not aware of any human preference.

Reward Modelling Phase

Reward model innovation: This is where the new innovation begins on how reward models are incorporated into RLHF. The idea behind the reward model is that a new LLM model, which can be same as the above mentioned base model, will have the ability to generate human preference score. The reason it is similar to a large language model is because this model also needs to understand the language semantics before it can rate if an output is human preferred or not. Since the reward is scalar, we add a linear layer on top of LLM to generate a scalar score in terms of human preference.

Data collection phase: This is done from the supervised fine tuning stage where the base model is asked to generate 2 outputs for a given text. Example: For an input token x, two output tokens are generated, y1 and y2 by the base model. These outputs are shown to human raters to rate and human preference is recorded for each individual output.

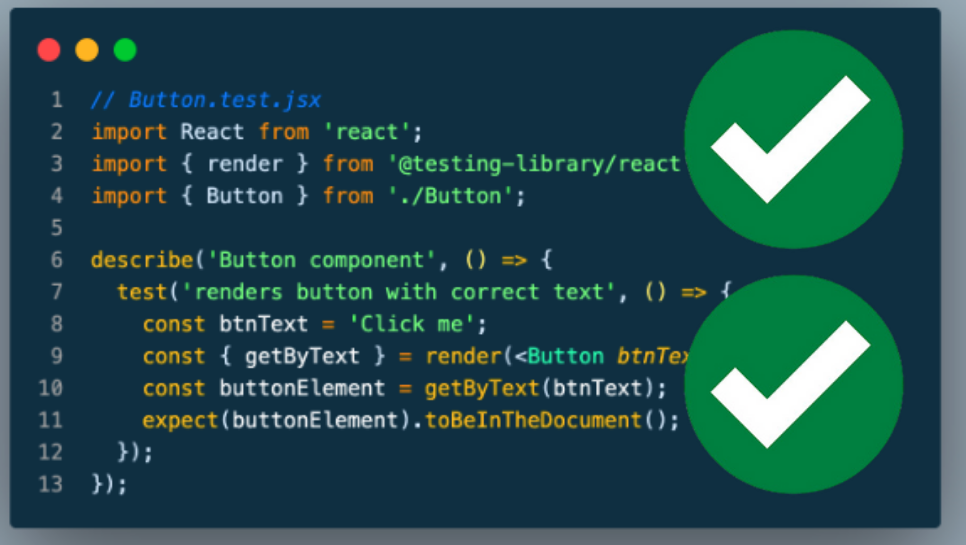
Training phase: Once the data sample is collected from the data collection phase, the reward model is trained with the following prompt. “Given the following input: <x>, LLM generated <y> output. Can you rate the performance of the output?”. The model will output r(reward) and we already know the actual value of reward r1 from the data collection phase. Now, this can be back-propagated with the loss function and the model can be trained. Below is the objective loss function which the model optimises for through back-propagation:

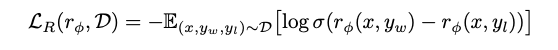
Notation:

• rΦ(x, y): a reward model parameterized by Φ which estimates the reward. Parameterized means we don’t know the actual value and this needs to be optimized from the above equation. This is the reward LLM model itself. Mostly, the LLM parameters are frozen here and only few parameters are left to change. Most important layer is the linear layer added at the top. This does most of the learning to rate the score of output.
• Ɗ: A dataset of triplets (x, yw, yl) where x: input, yw: the winner output and yl: the loser output
• σ: the sigmoid function which maps the difference in reward to a probability (0–1)
• ∑(x, y,w yl) ~Ɗ means x, yw, yl are all sampled from Ɗ

Example scenario: Imagine you’re training a reward model to evaluate responses. You have pairs of responses to a given prompt, and human feedback tells you which response is better. For context, x(“What is the capital of France?”), you have yw(“The capital of France is Paris.”) as winner and yl(“The capital of France is Berlin.” ) as loser. The reward model should eventually learn to give higher reward for “The capital of France is Paris.” output when compared to “The capital of France is Berlin.” output if “What is the capital of France?” input is given.

RL fine-tuning phase

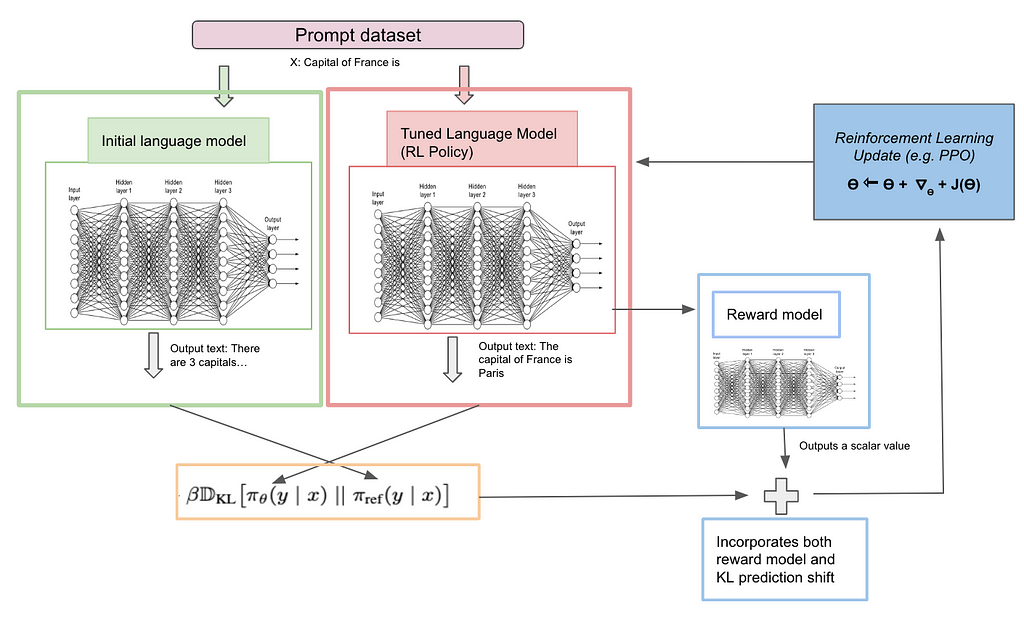
Reinforcement learning idea: Now the base model and reward model are trained, the idea is how to leverage reward model score and update base model parameters to reflect human preference. Since the reward model outputs a scalar score and is not differentiable, we cannot use simple back-propogation to update the base model param. Hence, we need other techniques to update the base model. This is where reinforcement learning comes which helps the base model to change the params through reward model score. This is done through PPO (proximal policy optimization). Understanding the core architecture of PPO is not required to grasp this concept and hence we will not cover it here but on a high level, the idea is that PPO can use scalar score to update base model parameters. Now let’s understand how base and reward models are incorporated to make base models learn human preference.

RL fine-tuning idea: In reinforcement learning, we have action, space and rewards. The idea is to come up with a policy which any action agent can take in the space which maximizes the reward. This becomes quite complicated but in a simplified sense, π is the policy which is our base LLM model only. Πref means the base model and ΠӨ means a different LLM optimal model which we are trying to generate. We need to find ΠӨ (the base model’s neural network weights will be fine-tuned) which gives human-preferred output. It’s just that we don’t know ΠӨ and the idea is to find this optimal model.

RL training and feedback loop phase: An input x is given to 2 policy models, Πref (baseline model) and ΠӨ (optimal model which we are trying to generate). Initially both models are kept the same. Input x to two models individually will give two outputs correspondingly. The output from ΠӨ model is also fed to reward model (input: x, output: y; as discussed above) and asked to output the reward score which is rΦ(x, y). Now we have 3 things, output from the baseline model, output from the optimal model, and a reward score from the optimal model. There are 2 things we are optimizing here, one is to maximize the reward because eventually we want the model to be as close as human preference and another is to minimize the divergence from baseline model. Maximizing the reward is easy since it is already a scalar quantity but how do we minimize the divergence of baseline and optimal model. Here we use “Kullback–Leibler divergence” which estimates the difference between 2 continuous probability distributions. Let’s take a deeper look into the objective loss function

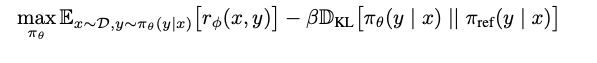
Notation:

• rΦ(x, y): a scalar value for an input x and output y (from optimal model). To be explicit, output from the optimal model is fed into the reward model.
• Dkl (ΠӨ (y | x) || Πref (y | x)): This computes the Kullback–Leibler divergence between 2 probability distributions. Each token from each model is a probability distribution. KL estimates how far the distribution is from each other.
• β : Hyperparameter which is used to determine how important it is to have optimal model close to baseline model.

Example scenario: Imagine you are asking (“What is the capital of France?”), Πref (baseline model) says: “The capital of France is Berlin.” and ΠӨ (optimal model) “There are 3 capitals, Paris, Versailles, and Lyon, but Paris is considered as the official capital”. Now rΦ(“x: What is the capital…”, “y: There are 3 capital..”) should give low score as it is less human-preferred and Kullback–Leibler divergence of (ΠӨ (y | x) || Πref (y | x)) should be high as well since the probability distribution space differs for both individual output. Hence the loss will be high from both terms. We do not want the model to only optimize for reward but also stay closer to the baseline model and hence both the terms are used to optimize the reward. In the next iteration with learning let’s say, ΠӨ (optimal model) says “The capital of France is Delhi”, in this case model learned to stay closer to Πref (baseline model) and output the format closer to baseline model but the reward component will still be lower. Hopefully, in the third iteration ΠӨ (optimal model) should be able to learn and output “The capital of France is Paris” with higher reward and model output aligning closely with baseline model.

The below diagram helps illustrate the logic. I will also highly recommend to go through RLHF link from hugging face.

What is Reinforcement learning through human feedback (RLHF) via reward-free method ?

With RLHF using a reward-based method in mind, let’s move to the reward-free method. According to the paper: “our key insight is to leverage an analytical mapping from reward functions to optimal policies, which enables us to transform a loss function over reward functions into a loss function over policies. This change-of-variables approach avoids fitting an explicit, standalone reward model, while still optimizing under existing models of human preferences”. Very complicated to understand, but let’s try to break this down in simple phases in the next section.

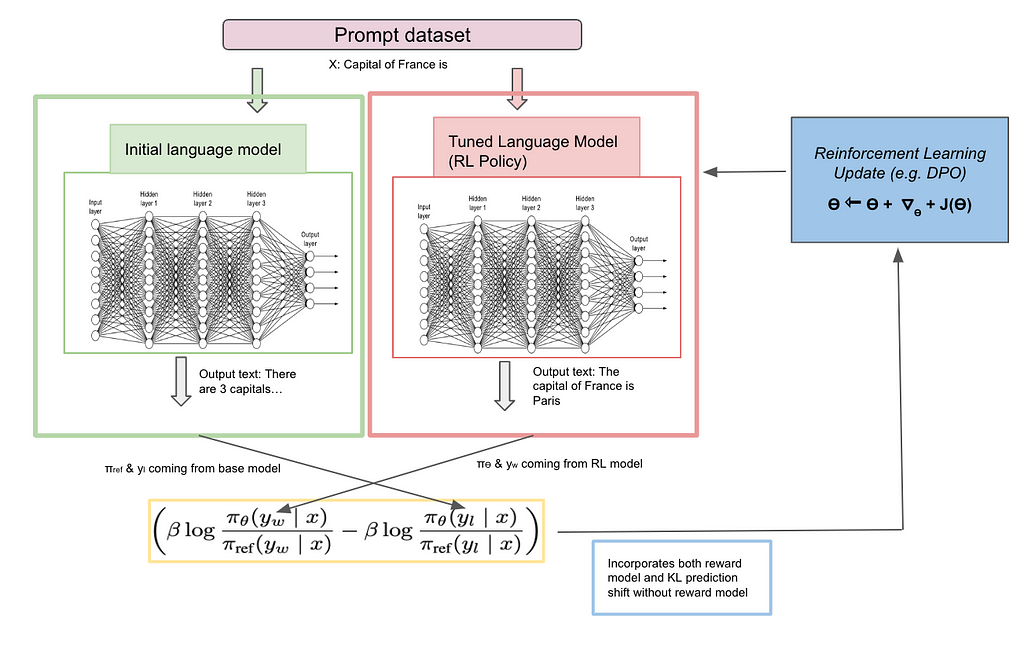
Reward-free method’s key idea: In RLHF, a separate new reward model is trained which is expensive and costly to maintain. Is there any mechanism to avoid training a new reward model and use the existing base model to achieve a new optimal model? This is exactly what reward-free method does i.e. it avoids training a new reward model and in turn changes the equation in such a way that there is no reward model term in the loss function of DPO (Direct preference optimization). One way to think about this is that we need to reach optimal model policy(ΠӨ) from base model (Πref). It can be reached either through optimizing the reward function space which helps build a proxy to reach optimal model policy or directly learning a mapping function from reward to policy and in turn optimize for policy itself. This is exactly what the authors have tried by removing the reward function component in loss function and substitute it directly by model policy parameter. This is what the author meant when they say “leverage an analytical mapping from reward function to optimal policies …. into a loss function over policies”. This is the core innovation of the paper.

DPO training and feedback loop phase: Using Πref (baseline model), input x is given and asked to produce 2 outputs (y1 and y2). All x, y1 and y2 are used by human raters to decide winning yw and losing yl. Offline data set is collected with triplet information <x, yw and yl>. With this information, we know what the winning (human preferred) and losing (human not preferred) answers are. Now, the same input x is given to 2 policy (models) Πref (baseline model) and ΠӨ (optimal model). Initially both models are kept the same for training purposes. Input x to two models individually will give two outputs correspondingly. We compute how far the output is from winning and losing answers from both reference and optimal model through “Kullback–Leibler divergence”. Let’s take a deeper look into the objective loss function

Equation

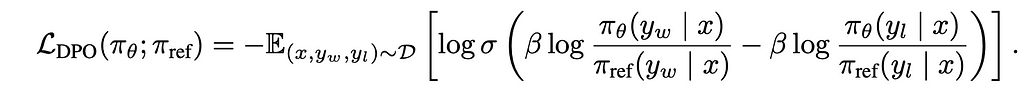
• ΠӨ (yw | x) -> Given x(input), how far is the corresponding output of the model say youtput from the winning output yw. Output youtput and yw are probability distributions and differences among both will be computed through “Kullback–Leibler divergence”. This will be a scalar value. Also this is computed for both models with different combinations of Πref (yw | x), Πref (yl | x), ΠӨ (yw | x) and ΠӨ (yl | x).
• β : Hyperparameter which is used to determine how important it is to have optimal model close to baseline model.

Conclusion

• Naturally, the question comes down to which one is better, RLHF through reward-based method using PPO or reward-free method using DPO. There is no right answer to this question. A recent paper compares “Is DPO superior to PPO for LLM alignment” (paper link) and concludes that PPO is generally better than DPO and that DPO suffers more heavily from out-of-distribution data. “Out-of-distribution” data means the human preference data is different from the baseline trained data. This can happen if base model training is done on some dataset while preference output is done for some other dataset.
• Overall, the research is still out on which one is better while we have seen companies like OpenAI, Anthropic, Meta leverage both RLHF via PPO and DPO as a tool for LLM alignment.

Reference

• Direct Preference Optimization: Your Language Model is Secretly a Reward Model: https://arxiv.org/pdf/2305.18290
• Is DPO Superior to PPO for LLM Alignment? A Comprehensive Study https://arxiv.org/pdf/2404.10719
• Hugging face RLHF article https://huggingface.co/blog/rlhf

---

LLM alignment: Reward-based vs reward-free methods was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Overview of PPCA, an extension of classical PCA, and its application to incomplete data via the EM Algorithm

Probabilistic Principal Components Analysis (PPCA) is a dimensionality reduction technique that leverages a latent variable framework to recover the directions of maximal variance in the data. When the noise follows an Isotropic Gaussian distribution, the probabilistic principal components will be closely related to the classical principal components, identical up to a scaling factor and an orthogonal rotation. PPCA can thus be used for many of the same applications as classical PCA, such as data visualization and feature extraction. The latent variable framework behind PPCA also offers functionality which classical PCA does not. For instance, PPCA can easily be extended to accommodate data with missing values, whereas classical PCA is undefined on incomplete data.

PPCA can be implemented using a number of different methods. Tipping and Bishop provided an implementation of PPCA via the EM algorithm in their original 1999 article; however, they did not explicitly show how the EM algorithm for PPCA extends to incomplete data. A previous article on Towards Data Science discussed an alternative approach to PPCA, which uses variational inference in place of the EM algorithm to impute missing values and derive the probabilistic principal components. This approach starts from the simplifying assumption that the standard deviation of the noise is known in advance, an assumption which makes it easier to optimize the variational distribution but is not representative of most applications. For this post, I will focus on the EM algorithm, expanding upon previous discussions by illustrating all of the steps needed to extend Tipping and Bishop’s EM algorithm for PPCA to incomplete data.

Overview of PPCA and its Relationship to Classical PCA:

Classical PCA is a deterministic method which does not model the data in terms of distinct signal and noise components. By contrast, PPCA is derived from a probabilistic model of the form

where z_i is a vector of q unobserved latent variables, W is a loading matrix that maps the q latent variables into the p observed variables, and epsilon_i is a noise term which makes the procedure probabilistic rather than deterministic. It’s typically assumed that z_i follows a standard normal distribution. The noise term, epsilon_i, must follow an Isotropic Gaussian distribution with mean zero and a covariance matrix of the form sigma ^2 I for the relationship between PPCA and classical PCA to hold.

Under this latent variable model, Tipping and Bishop (1999) have shown that the directions of maximal variance in the data can be recovered through maximum likelihood estimation. They prove that the MLEs for W and sigma are given by

Here, U_q is the matrix whose columns are the q principal eigenvectors of the sample covariance matrix, Lambda_q is a diagonal matrix of the eigenvalues corresponding to the q principal eigenvectors, and R is an arbitrary orthogonal rotation matrix. Note that the classical principal components are given by the matrix U_q. As a result of the other terms in the expression for W_MLE, the probabilistic principal components may have different scalings and different orientations than the classical components, but both sets of components will span the same subspace and can be used interchangeably for most applications requiring dimensionality reduction.

In practice, the identity matrix can be substituted for the arbitrary orthogonal matrix R to calculate W_MLE. Using the identity matrix not only reduces the computational complexity but also ensures that there will be a perfect correlation or anti-correlation between the probabilistic principal components and their classical counterparts. These closed-form expressions are very convenient for complete data, but they cannot directly be applied to incomplete data. An alternative option for finding W_MLE, which can easily be extended to accommodate incomplete data, is to use the EM algorithm to iteratively arrive at the maximum likelihood estimators, in which case R will be arbitrary at convergence. I’ll briefly review the EM algorithm below before illustrating how it can be used to apply PPCA to incomplete data.

EM Algorithm for PPCA with Missing Data:

The EM algorithm is an iterative optimization method which alternates between estimating the latent variables and updating the parameters. Initial values must be specified for all parameters at the beginning of the EM algorithm. In the E-Step, the expected value of the log-likelihood is computed with respect to the current parameter estimates. The parameter estimates are then re-calculated to maximize the expected log-likelihood function in the M-Step. This process repeats until the change in the parameter estimates is small and the algorithm has thus converged.

Before illustrating how the EM algorithm for PPCA extends to incomplete data, I will first introduce some notation. Suppose that we observe D different combinations of observed and unobserved predictors in the data. The set of D combinations will include the pattern where all predictors are observed, assuming the data contains at least some complete observations. For each distinct combination d=1,…,D, let x_1,…,x_n_d denote the set of observations which share the dth pattern of missing predictors. Each data point in this set can be decomposed as

where the subscripts obs_d and mis_d denote which predictors are observed and unobserved in the dth combination.

The algorithm in the image above shows all of the steps needed to apply PPCA to incomplete data, using my notation for observed and unobserved values. To initialize the parameters for the EM algorithm, I impute any missing values with the predictor means and then use the closed-form estimators given by Tipping and Bishop (1999). The mean-imputed estimates may be biased, but they provide a more optimal starting point than a random initialization, reducing the likelihood of the algorithm converging to a local minimum. Note that the imputed data is not used beyond the initialization.

In the E-step, I first compute the expectation of each z_i with respect to the observed values and the current parameter estimates. Then I treat the missing values as additional latent variables and compute their expectation with respect to the current parameters and z_i. In the M-step, I update the estimates for W, mu, and sigma based on the expected log-likelihood that was computed in the E-Step. This differs from Tipping and Bishop’s EM algorithm for complete data, where mu is estimated based on the sample mean and only W and sigma are iteratively updated in the EM algorithm. It is not necessary to iteratively estimate mu when X is complete or when the unobserved values are missing completely at random since the sample mean is the MLE. For other patterns of missingness, however, the mean of the observed values is generally not the MLE, and the EM algorithm will yield more accurate estimates of mu by accounting for the likely values of the missing data points. Thus, I’ve included the update for mu in the M-Step along with the other parameter updates.

Python Implementation:

I have provided an implementation of the EM algorithm for PPCA here, following the steps of the algorithm above to accommodate missing data. My function requires the user to specify the data matrix and the number of components in PPCA (i.e., q, the latent variable dimension). Common techniques for selecting the number of components in classical PCA can also be applied to PPCA when the latent variable dimension is not known. For instance, one option for selecting q would be to create a scree plot and apply the so-called ‘elbow method.’ Alternatively, q could be chosen through cross-validation.

I will now consider three different simulations to test my implementation of the EM algorithm for PPCA: one without any missing values, one with missing values that are selected completely at random, and one with missing values that are selected not-at-random. To simulate data that is missing completely at random, I assume that each of the nxp values has an equal 10% chance of being unobserved. Meanwhile, to simulate data that is missing not-at-random, I assume that data points with a higher z-score have a greater chance of being unobserved, with an expected proportion of 10% missing overall.

I use the same synthetic data for all simulations, simply altering the pattern of missingness to assess the performance on incomplete data. To generate the data, I let n=500, p=30, and q=3. I sample both W and mu from a Uniform[-1, 1] distribution. Then I draw the latent variables z_i, i=1,…,n from a standard normal distribution and the noise terms epsilon_i, i=1,…,n, from an Isotropic Gaussian distribution with sigma=0.7. I assume that q is correctly specified in all simulations. For additional details, see the simulation code here.

To evaluate the accuracy of the EM algorithm, I report the relative error of the parameter estimates. The relative error for mu is reported with respect to the l2 norm, and the relative error for W is reported with respect to the Frobenius norm. Since W can only be recovered up to an orthogonal rotation, I have used NumPy’s orthogonal prosecutes function to rotate the estimated matrix W in the direction of the true W before computing the relative error.

My results confirm that the EM algorithm can accurately estimate the parameters in all three of these setups. It is not surprising that the EM algorithm performs well in the complete data simulation since the initialization should already be optimal. However, it is more noteworthy that the accuracy remains high when missing values are introduced. The parameter estimates even show a relatively high degree of robustness to non-random patterns of missingness, at least under the assumed setup for this simulation. For real datasets, the performance of the EM algorithm will depend on a number of different factors, including the accuracy of the initialization, the pattern of missingness, the signal to noise ratio, and the sample size.

Conclusion:

Probabilistic principal components analysis (PPCA) can recover much of the same structure as classical PCA while also extending its functionality, for instance, by making it possible to accommodate data with missing values. In this article, I have introduced PPCA, explored the relationship between PPCA and classical PCA, and illustrated how the EM algorithm for PPCA can be extended to accommodate missing values. My simulations indicate that the EM algorithm for PPCA yields accurate parameter estimates when there are missing values, even demonstrating some robustness when values are missing not-at-random.

References:

M. Tipping, C. Bishop, Probabilistic principal component analysis (1999). Journal of the Royal Statistical Society Series B: Statistical Methodology.

---

Principal Components Analysis (PCA) Through a Latent Variable Lens was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Evaluating machine learning models beyond training data

Introduction

In recent years, data-driven approaches such as machine learning (ML) and deep learning (DL) have been applied to a wide range of tasks including machine translation and personal customized recommendations. These technologies reveal some patterns within the given training dataset by analyzing numerous data. However, if the given dataset has some biases and does not include the data that you want to know or predict, it might be difficult to get the correct answer from the trained model.

Let’s think about the case of ChatGPT. The latest version of ChatGPT at this time is ChatGPT 4o, and this model is trained on data until June 2023 (at the period of this article). Therefore, if you ask about something that happened in 2024 not included in the training data, you will not get an accurate answer. This is well-known as “hallucination,” and OpenAI added the preprocessing procedure to return a fixed answer as “unanswerable” for such kinds of questions. ChatGPT’s training data is also basically based on documents written in English, so it is not good at local domain knowledge outside of English-native countries such as Japan and France. Therefore, many companies and research groups put a lot of effort into customizing their LLM by including the region or domain-specific knowledge using RAG (Retrieval-Augmented Generation) or fine-tuning.

Hence, identifying what training data is used is important for understanding the applicability and limitations of AI models. On the other hand, one of the biggest challenges in data-driven approaches is that these technologies often need to perform beyond the range of the training dataset. These demands are typically seen in new product development in material science, predicting the effects of new pharmaceutical compounds, and predicting consumer behavior when launching products in the markets. These scenarios require the correct predictions in the sparse area and outside of the training data, which refer to interpolation and extrapolation.

Interpolation involves making predictions within the known data range. If the training data is densely and uniformly distributed, accurate predictions can be obtained within that range. However, in practice, preparing such data is uncommon. On the other hand, extrapolation refers to making predictions outside the known data points’ range. Although predictions in such areas are highly desired, data-driven approaches typically struggle the most. Consequently, it is significantly important to understand the performance of both interpolation and extrapolation for each algorithm.

This article examines various machine learning algorithms for their interpolation and extrapolation capabilities. We prepare an artificial training dataset and evaluate these capabilities by visualizing each model’s prediction results. The target of machine learning algorithms are as follows:

• Symbolic Regressor
• SVR (Support Vector Regression)
• Gaussian Process Regressor (GPR)
• Decision Tree Regressor
• Random Forest Regressor
• XGBoost
• LightGBM

In addition, we also evaluate ensemble models such as Voting Regressor and Stacking Regressor.

Codes

Full of codes are available from below:

blog_TDS/02_compare_regression at main · rkiuchir/blog_TDS

Data Generation and Preprocessing

Firstly, we generate the artificial data using a simple nonlinear function that is slightly modified from the symbolic regressor’s tutorial in gplearn by adding the exponential term. This function consists of linear, quadratic, and exponential terms, defined as follows:

where x₀ and x₁ take a range of -1 to 1. The plane of ground truth is as shown below:

Since we examine the performance of each ML model in terms of interpolation and extrapolation, different datasets will be needed for each case.

For interpolation, we evaluate the model performance within the same range as with the training dataset. Therefore, each model will be trained with discretized data points within the range of -1 to 1 and evaluated the predicted surface within the same range.

On the other hand, for extrapolation, the capability of the model within the range outside of the training dataset will be required. We will train the model using the discretized data points within the range of -0.5 to 1 for both x₀ and x₁ and assess the predicted surface within the range of -1 to 1. Consequently, the difference between the ground truth and predicted surface in the range of -1 to -0.5 for both x₀ and x₁ reveals the model capability in terms of extrapolation.

In this article, the impact of the number of points for the training dataset will be evaluated by examining two cases: 20 and 100 points.

For example, 100 data points are generated as follows:

import numpy as np

def target_function(x0, x1):
    return x0**2 - x1**2 + x1 + np.exp(x0) - 1

# Generate training data for interpolation
X_train = rng.uniform(-1, 1, 200).reshape(100, 2)
y_train = target_function(X_train[:, 0], X_train[:, 1])

# Generate training data for extrapolation
X_train = rng.uniform(-0.5, 1, 200).reshape(100, 2)
y_train = target_function(X_train[:, 0], X_train[:, 1])

Introduction to Machine Learning Algorithms

In this article, we evaluate the performance of interpolation and extrapolation for the major 7 machine learning algorithms. In addition, the 6 ensemble models using 7 algorithms are also considered. Each algorithm has different structures and aspects, that introduce pros and cons for predicting performance. Here we summarize the characteristics of each algorithm as follows:

1. Symbolic Regression

• A trained model is expressed as the mathematical expressions fitted based on the genetic algorithms
• Model is defined as the function, contributing high interpretability
• Appropriate for the task that target variable can be expressed as a function of features
• Good at interpolation but may have some potential in extrapolation

Find Hidden Laws Within Your Data with Symbolic Regression

2. Support Vector Regression (SVR)

• Based on a Support Vector Machine (SVM) that can efficiently handle the nonlinear relationship in the high dimensional spaces using the kernel method
• Using different types of kernels such as linear, RBF, polynomial, and sigmoid kernels, a model can express complex data patterns
• Good at interpolation but less stable in extrapolation

The Complete Guide to Support Vector Machine (SVM)

3. Gaussian Process Regression (GPR)

• Based on the Bayesian method, the prediction is expressed as the probability which includes the predicted value and its uncertainty
• Thanks to the uncertainty estimation, GPR used for Bayesian Optimization
• Using different types of kernels such as linear, RBF, polynomial, and sigmoid kernels, a model can express complex data patterns
• Good at interpolation, and some potential for extrapolation selecting appropriate kernel selection

Quick Start to Gaussian Process Regression

4. Decision Tree

• Simple tree-shape algorithm which successively splits the data
• Easy to understand and interpret but tends to overfit
• Step-like estimation for interpolation and not good at extrapolation

Decision Tree in Machine Learning

5. Random Forest

• An ensemble-based algorithm which is called “Bagging” consisting of multiple decision trees
• By combining multiple diverse trees, this algorithm can reduce overfitting risk and have a high interpolation performance
• More stable predictions than single decision trees but not good at extrapolation

Understanding Random Forest

6. XGBoost

• An ensemble-based algorithm which is called “Boosting” combines multiple decision trees by sequentially reducing errors
• Commonly used for competition such as Kaggle because of the good prediction performance
• More stable predictions than single decision trees but not good at extrapolation

XGBoost: A Deep Dive into Boosting

7. LightGBM

• Similar to XGBoost, but with faster training speed and memory efficiency, which is more suitable for the larger datasets
• More stable predictions than single decision trees but not good at extrapolation

What is LightGBM, How to implement it? How to fine tune the parameters?

8. Voting Regressor

• An ensemble learning method combining predictions from multiple models
• Mixing different model characteristics, which contribute to more robust predictions than a single model
• Evaluated in three combinations in this article:
  – Support Vector Regressor + Random Forest
  – Gaussian Process Regressor + Random Forest
  – Random Forest + XGBoost

VotingRegressor

9. Stacking Regressor

• An ensemble learning method that uses predictions from multiple models as input for a final prediction model, “meta-model”
• Meta model covers individual model weaknesses and combines each model’s strengths
• Evaluated in three combinations in this article:
  – Base model: Support Vector Regressor + Random Forest; Meta-model: Random Forest
  – Base model: Gaussian Process Regressor + Random Forest; Meta-model: Random Forest
  – Base model: Random Forest + XGBoost; Meta-model: Random Forest

StackingRegressor

Using these algorithms, we will evaluate both interpolation and extrapolation performance with the dataset we generated earlier. In the following sections, the training methods and evaluation approaches for each model will be explained.

Model Training and Evaluation

Preprocessing

Basically, except for tree-based approaches such as Random Forest, XGBoost, and LightGBM, most machine learning algorithms require feature scaling. However, since we only use two features such as x₀ and x₁ which take the same range, -1 to 1 (interpolation) or -0.5 to 1 (extrapolation) in this practice, we will skip the feature scaling.

Model Training

For simplicity, parameter tuning is not done for all algorithms except LightGBM of which default parameters are suitable for the larger dataset.

As introduced in the earlier section, we will use different datasets for the evaluation of interpolation and extrapolation during model training.

Evaluation and Visualization

After model training, we will predict using very finely discretized data. Based on these predicted values, the prediction surface will be drawn using the Plotly surface function.

These procedures are done by the following code:

class ModelFitterAndVisualizer:
    def __init__(self, X_train, y_train, y_truth, scaling=False, random_state=41):
        """
        Initialize the ModelFitterAndVisualizer class with training and testing data.

        Parameters:
            X_train (pd.DataFrame): Training data features
            y_train (pd.Series): Training data target
            y_truth (pd.Series): Ground truth for predictions
            scaling (bool): Flag to indicate if scaling should be applied
            random_state (int): Seed for random number generation
        """
        self.X_train = X_train
        self.y_train = y_train
        self.y_truth = y_truth
        
        self.initialize_models(random_state)
        
        self.scaling = scaling

    # Initialize models
    # -----------------------------------------------------------------
    def initialize_models(self, random_state):
        """
        Initialize the models to be used for fitting and prediction.

        Parameters:
            random_state (int): Seed for random number generation
        """
                
        # Define kernel for GPR
        kernel = 1.0 * RBF(length_scale=1.0) + WhiteKernel(noise_level=1.0)
        
        # Define Ensemble Models Estimator
        # Decision Tree + Kernel Method
        estimators_rf_svr = [
            ('rf', RandomForestRegressor(n_estimators=30, random_state=random_state)),
            ('svr', SVR(kernel='rbf')),
        ]
        estimators_rf_gpr = [
            ('rf', RandomForestRegressor(n_estimators=30, random_state=random_state)),
            ('gpr', GaussianProcessRegressor(kernel=kernel, normalize_y=True, random_state=random_state))
        ]
        # Decision Trees
        estimators_rf_xgb = [
            ('rf', RandomForestRegressor(n_estimators=30, random_state=random_state)),
            ('xgb', xgb.XGBRegressor(random_state=random_state)),
        ]
        
        self.models = [
            SymbolicRegressor(random_state=random_state),
            SVR(kernel='rbf'),
            GaussianProcessRegressor(kernel=kernel, normalize_y=True, random_state=random_state),
            DecisionTreeRegressor(random_state=random_state),
            RandomForestRegressor(random_state=random_state),
            xgb.XGBRegressor(random_state=random_state),
            lgbm.LGBMRegressor(n_estimators=50, num_leaves=10, min_child_samples=3, random_state=random_state),
            VotingRegressor(estimators=estimators_rf_svr),
            StackingRegressor(estimators=estimators_rf_svr, 
                              final_estimator=RandomForestRegressor(random_state=random_state)),
            VotingRegressor(estimators=estimators_rf_gpr),
            StackingRegressor(estimators=estimators_rf_gpr, 
                              final_estimator=RandomForestRegressor(random_state=random_state)),
            VotingRegressor(estimators=estimators_rf_xgb),
            StackingRegressor(estimators=estimators_rf_xgb, 
                              final_estimator=RandomForestRegressor(random_state=random_state)),
        ]
        
        # Define graph titles
        self.titles = [
            "Ground Truth", "Training Points", 
            "SymbolicRegressor", "SVR", "GPR",
            "DecisionTree", "RForest", 
            "XGBoost", "LGBM", 
            "Vote_rf_svr", "Stack_rf_svr__rf",
            "Vote_rf_gpr", "Stack_rf_gpr__rf",
            "Vote_rf_xgb", "Stack_rf_xgb__rf",
        ] 

    def fit_models(self):
        """
        Fit the models to the training data.

        Returns:
            self: Instance of the class with fitted models
        """
        if self.scaling:
            scaler_X = MinMaxScaler()
            self.X_train_scaled = scaler_X.fit_transform(self.X_train)
        else:
            self.X_train_scaled = self.X_train.copy()
        
        for model in self.models:
            model.fit(self.X_train_scaled, self.y_train)
        return self

    def visualize_surface(self, x0, x1, width=400, height=500,
                          num_panel_columns=5,
                          vertical_spacing=0.06, horizontal_spacing=0,
                          output=None, display=False, return_fig=False):
        """
        Visualize the prediction surface for each model.

        Parameters:
            x0 (np.ndarray): Meshgrid for feature 1
            x1 (np.ndarray): Meshgrid for feature 2
            width (int): Width of the plot
            height (int): Height of the plot
            output (str): File path to save the plot
            display (bool): Flag to display the plot
        """
        
        num_plots = len(self.models) + 2
        num_panel_rows = num_plots // num_panel_columns
        
        whole_width = width * num_panel_columns
        whole_height = height * num_panel_rows

        specs = [[{'type': 'surface'} for _ in range(num_panel_columns)] for _ in range(num_panel_rows)]
        fig = make_subplots(rows=num_panel_rows, cols=num_panel_columns, 
                            specs=specs, subplot_titles=self.titles,
                            vertical_spacing=vertical_spacing, 
                            horizontal_spacing=horizontal_spacing)

        for i, model in enumerate([None, None] + self.models):
            # Assign the subplot panels
            row = i // num_panel_columns + 1
            col = i % num_panel_columns + 1
            
            # Plot training points
            if i == 1:
                fig.add_trace(go.Scatter3d(x=self.X_train[:, 0], y=self.X_train[:, 1], z=self.y_train,
          mode='markers', marker=dict(size=2, color='darkslategray'),
          name='Training Data'), row=row, col=col) 
                
                surface = go.Surface(z=self.y_truth, x=x0, y=x1, 
                                     showscale=False, opacity=.4)
                fig.add_trace(surface, row=row, col=col)
            
            # Plot predicted surface for each model and ground truth
            else:
                y_pred = self.y_truth if model is None else model.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)
                surface = go.Surface(z=y_pred, x=x0, y=x1, 
                                     showscale=False)
                fig.add_trace(surface, row=row, col=col)


            fig.update_scenes(dict(
                xaxis_title='x0',
                yaxis_title='x1',
                zaxis_title='y',
                ), row=row, col=col)
                      
        fig.update_layout(title='Model Predictions and Ground Truth', 
                          width=whole_width, 
                          height=whole_height)
        
        
        # Change camera angle
        camera = dict(
         up=dict(x=0, y=0, z=1),
         center=dict(x=0, y=0, z=0),
         eye=dict(x=-1.25, y=-1.25, z=2)
        )
        for i in range(num_plots):
            fig.update_layout(**{f'scene{i+1}_camera': camera})

                
        if display:
            fig.show()
        
        if output:
            fig.write_html(output)
            
        if return_fig:
            return fig

Evaluation of Interpolation Performance

The prediction surfaces for each algorithm are shown for training data cases of 100 and 20 points respectively.

100 Training Points:

20 Training Points:

Here are the summarized features for each algorithm:

Symbolic Regressor

This algorithm performs almost perfectly in interpolation even with as few as 20 data points. This is because the Symbolic Regressor approximates the mathematical expressions and the simple functional form is used in this practice. Thanks to this feature, the predicted surface is notably smooth which is different from the tree-based algorithms explained later.

Support Vector Regressor (SVR), Gaussian Process Regressor (GPR)

For kernel-based algorithms SVR and GPR, although the predicted surfaces slightly differ from the ground truth, interpolation performance is generally good with 100 data points. In addition, the prediction surface obtained from these models is smooth similar to one estimated by Symbolic Regressor. However, in the case of 20 points, there is a significant difference between the predicted surface and the ground truth especially for SVR.

Decision Tree, Random Forest, XGBoost, LightGBM

Firstly, the prediction surfaces estimated by these five tree-based models are not smooth but more step-like shapes. This characteristic arises from the structure and learning method of decision trees. Decision trees split the data recursively based on a threshold for one of the features. Each data point is assigned to some leaf nodes whose values are represented as the average value of the data points in that node. Therefore, the prediction values are constant within each leaf node, resulting in a step-like prediction surface.

The estimates of a single decision tree clearly show this characteristic. On the other hand, ensemble methods like Random Forests, XGBoost, and LightGBM, which consist of many decision trees within a single model, generate relatively smoother prediction surfaces due to the more different thresholds based on the many different shapes of decision trees.

Voting Regressor, Stacking Regressor

The Voting Regressor combines the results of two algorithms by averaging them. For combinations like Random Forest + SVR, and Random Forest + GPR, the prediction surfaces reflect characteristics that mix the kernel-based and tree-based models. On the other hand, the combination of tree-based models like Random Forest and XGBoost relatively reduces the step-like shape prediction surface than one estimated from the single model.

The Stacking Regressor, which uses a meta-model to compute final predictions based on the outputs of multiple models, also shows step-like surfaces, because of the Random Forest used as the meta-model. This characteristic will be changed if kernel-based algorithms like SVR or GPR are used as the meta-model.

Evaluation of Extrapolation Performance

As explained earlier, each model is trained with data ranging from -0.5 to 1 for both x₀ and x₁ and those performances will be evaluated within the range of -1 to 1. Therefore, we get to know the extrapolation ability to inspect the prediction surface with the range of -1 to -0.5 for both x₀ and x₁.

The prediction surfaces for each algorithm are shown for training data cases of 100 and 20 points respectively.

100 Training Points:

20 Training Points:

Symbolic Regressor

The predicted surface within the area of extrapolation obtained by the Symbolic Regressor which is trained with 100 data points is almost accurately estimated similar to the interpolation evaluation. However, with only 20 training data points used, the predicted surface differs from the ground truth especially in the edge of the surface, indicating that the obtained functional form is not well estimated.

Support Vector Regressor (SVR), Gaussian Process Regressor (GPR)

Although both SVR and GPR are kernel-based algorithms, the obtained results are totally different. For both of 20 and 100 data points, while the predicted surface from SVR is well not estimated, GPR predicts almost perfectly even within the range of extrapolation.

Decision Tree, Random Forest, XGBoost, LightGBM

Although there are some differences among the results from these tree-based models, the predicted surfaces are constant in the range of extrapolation. This is because that decision trees rely on splits and no splits are generated in extrapolation regions, which cause constant values.

Voting Regressor, Stacking Regressor

As seen above, the kernel-based algorithms have better performance compared to the tree-based ones. The Voting Regressor with the combination of Random Forest and XGBoost, and all three Stacking Regressors whose meta-model is Random Forest predict constant in the range of extrapolation. On the other hand, the prediction surfaces derived from the Voting Regressor with the combination of Random Forest + SVR, and Random Forest + GPR have the blended characteristics of kernel-based and tree-based models.

Summary

In this article, we evaluated the interpolation and extrapolation performance of the various machine learning algorithms. Since the ground truth data we used is expressed as a simple functional foam, symbolic regressor and kernel-based algorithms provide a better performance, especially for extrapolation than tree-based algorithms. However, more complex tasks that cannot be expressed in mathematical formulas might bring different results.

Thank you so much for reading this article! I hope this article helps you understand the interpolation and extrapolation performance of machine learning models, making it easier to select and apply the right models for your projects.

Links

Other articles

• How OpenAI’s Sora is Changing the Game: An Insight into Its Core Technologies
• Create “Interactive Globe + Earthquake Plot in Python
• Pandas Cheat Sheet for Data Preprocessing

Personal website

R. Kiuchi – Seismology

---

The Machine Learning Guide for Predictive Accuracy: Interpolation and Extrapolation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

LLM Apps, Crucial Data Skills, Multi-Agent AI Systems, and Other July Must-Reads

Feeling inspired to write your first TDS post? We’re always open to contributions from new authors.

If it’s already summer where you live, we hope you’re making the most of the warm weather and (hopefully? maybe?) more relaxed daily rhythms. Learning never stops, of course—at least not for data scientists—so if your idea of a good time includes diving into new challenges and exploring cutting-edge tools and workflows, you’re in for a treat.

Our July highlights, made up of the articles that created the biggest splash among our readers last month, cover a wide range of practical topics—and many of them are geared towards helping you raise your own bar and expand your skill set. Let’s dive in!

Monthly Highlights

• What 10 Years at Uber, Meta and Startups Taught Me About Data Analytics
  Giving advice is easy; offering actionable, time-tested insights based on 10 years of diverse experience in data leadership takes quite a bit more effort —and in the case of Torsten Walbaum’s article, it very much pays off.
• How I Use ChatGPT as a Data Scientist
  Are we finally at the point where LLM-based tools can significantly streamline data professionals’ core tasks? As Egor Howell explains, if you make smart choices about how and where to integrate ChatGPT into your workflow, your productivity might already stand to reap major benefits.
• 330 Weeks of Data Visualizations: My Journey and Key Takeaways
  After creating weekly data visualization for more than five years, Yu Dong reflects on the value of consistency, and shares helpful pointers for current and aspiring data scientists who’d like to level-up their craft when creating charts, plots, and infographics.

• Building LLM Apps: A Clear Step-By-Step Guide
  Many ML practitioners have great ideas for AI-based products, yet, as Almog Baku points out, “there are no established best practices, and often, pioneers are left with no clear roadmap, needing to reinvent the wheel or getting stuck.” Fortunately, that’s no longer the case, now that Almog has put together a blueprint for navigating the complex landscape of LLM-native development.
• Multi AI Agent Systems 101
  Soon after LLMs went mainstream, product engineers started to discover all the various pain points and bottlenecks they create. Mariya Mansurova’s recent guide introduces one of the most promising strategies for addressing these challenges: multi-agent AI systems, where teams of agents, each with their own specialized “skill,” can collaborate with each other.
• The 5 Data Science Skills You Can’t Ignore in 2024
  In her excellent career-focused roundup, Sara Nóbrega observes that “while universities and formal education provide some essential skills, they often do not prepare students with the practical know-how needed in companies.” Sara aims to fill in this gap with recommendations for five areas data scientists should focus on in order to thrive in today’s job market.
• 17 (Advanced) RAG Techniques to Turn Your LLM App Prototype into a Production-Ready Solution
  For a one-stop, comprehensive resource you can refer to whenever you need to tweak, refine, or upgrade your retrieval-augmented generation system, make sure to bookmark Dominik Polzer’s recent contribution, which goes well beyond the basics to cover metadata, query routing, sentence-window retrieval, and much more.
• Fine-Tune Smaller Transformer Models: Text Classification
  We round out our monthly lineup with a standout project walkthrough, courtesy of Ida Silfverskiöld: it patiently outlines the process of fine-tuning a smaller transformer model for an NLP task, working with a pre-trained encoder model with binary classes to identify clickbait vs. factual articles.

Our latest cohort of new authors

Every month, we’re thrilled to see a fresh group of authors join TDS, each sharing their own unique voice, knowledge, and experience with our community. If you’re looking for new writers to explore and follow, just browse the work of our latest additions, including Mengliu Zhao, Robbie Geoghegan, Alex Dremov, Torsten Walbaum, Jeremi Nuer, Jason Jia, Akchay Srivastava, Roman S, James Teo, Luis Fernando PÉREZ ARMAS, Ph.D., Lea Wu, W. Caden Hamrick, Jack Moore, Eddie Forson, Carsten Frommhold, Danila Morozovskii, Biman Chakraborty, Jean Meunier-Pion, Ken Kehoe, Robert Lohne, Pranav Jadhav, Cornellius Yudha Wijaya, Vito Rihaldijiran, Justin Laughlin, Yiğit Aşık, Teemu Sormunen, Lars Wiik, Rhea Goel, Ryan D’Cunha, Gonzalo Espinosa Duelo, Akila Somasundaram, Mel Richey, PhD, Loren Hinkson, Jonathan R. Williford, PhD, Daniel Low, Nicole Ren, Daniel Pollak, Stefan Todoran, Daniel Khoa Le, Avishek Biswas, Eyal Trabelsi, Ben Olney, Michael B Walker, Eleanor Hanna, and Magda Ntetsika.

Thank you for supporting the work of our authors! We love publishing articles from new authors, so if you’ve recently written an interesting project walkthrough, tutorial, or theoretical reflection on any of our core topics, don’t hesitate to share it with us.

Until the next Variable,

TDS Team

---

LLM Apps, Crucial Data Skills, Multi-AI Agent Systems, and Other July Must-Reads was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.