
Efficient geodata management for optimized search in real-world applications

Introduction
Google Maps and Uber are only some examples of the most popular applications working with geographical data. Storing information about millions of places in the world obliges them to efficiently store and operate on geographical positions, including distance calculation and search of the nearest neighbours.
All modern geographical applications use 2D locations of objects represented by longitude and latitude. While it might seem naive to store the geodata in the form of coordinate pairs, there are some pitfalls in this approach.
In this article, we will discuss the underlying issues of the naive approach and talk about another modern format used to accelerate data manipulation in large systems.
Note. In this article, we will represent the world as a large flat 2D rectangle instead of a 3D ellipse. Longitude and latitude will be represented by X and Y coordinates respectively. This simplification will make the explanation process easier without omitting the main details.
Problem
Let us imagine a database storing 2D coordinates of all application objects. A user logs in to the application and wants to find the nearest restaurants.
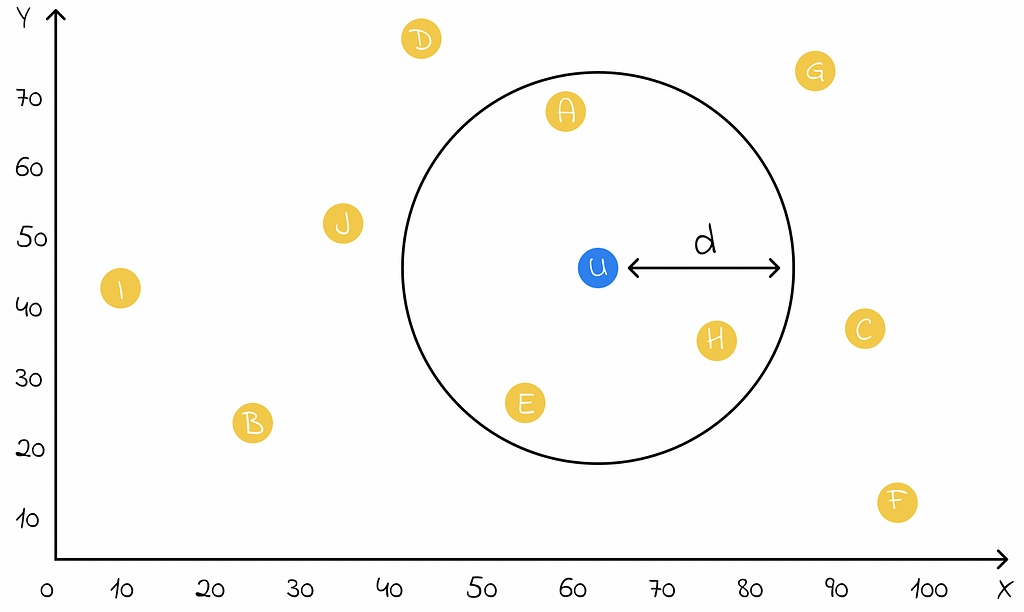
If coordinates are simply stored in the database, then the only way to answer this type of query is to linearly iterate through all of the possible objects and filter the closest ones. Obviously, this is not a scalable approach and search would be extremely slow in the real application.
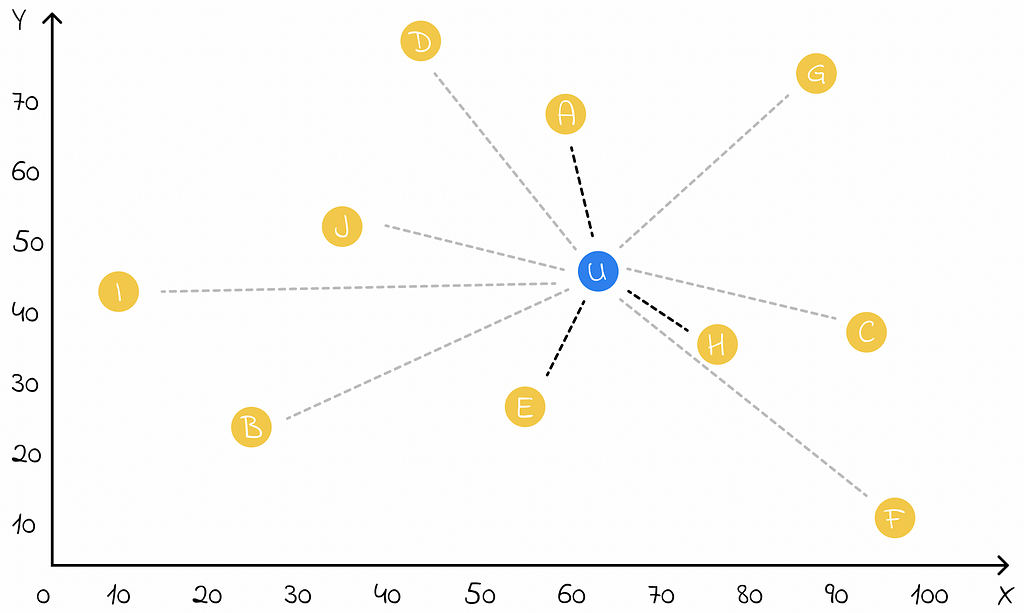
SQL databases allow the creation of an index — a data structure built on a certain column of a table accelerating the search process by keys in that column.
Another approach includes creating an index on one of the coordinate columns. When a user performs a query, the database can in O(1) time retrieve the position of the row in the table corresponding to the current position of the user.
Thanks to the constructed index, the database can also rapidly find the rows with the nearest coordinate value. Then it is possible to take a set of such rows and then filter those whose total Euclidean distance from the user position is less than a certain search radius.
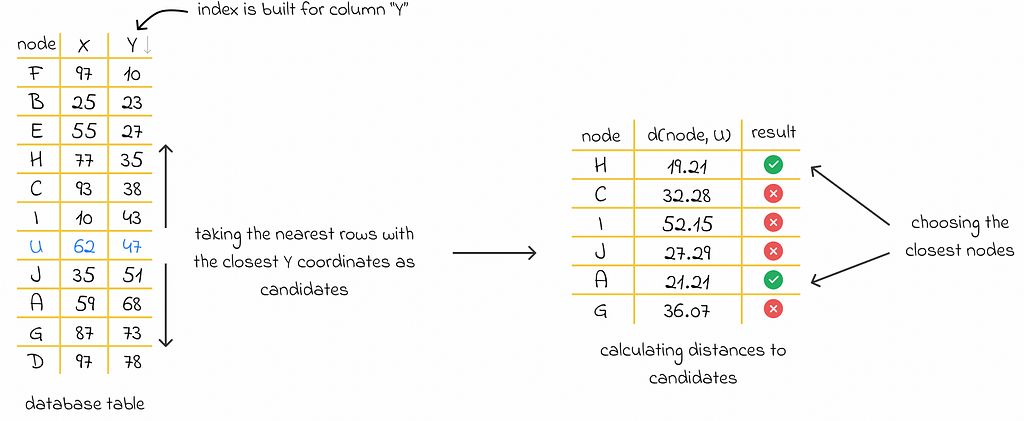
While the described approach is better than the previous one, it requires time to filter rows with the closest distances. Additionally, there can be cases when initially selected rows with the closest coordinates are not actually the closest ones to the user position.
A single table cannot have two indexes simultaneously. That is why for solving this problem, both coordinates should be represented as a single combined value while preserving information about distances. This objective is exactly achieved by quadtrees which are discussed in the next section.
Quadtree
A quadtree is a tree data structure used for recursive partitioning of a 2D space into four quadrants. Depending on the tree structure, every parent node can have from 0 to 4 children.
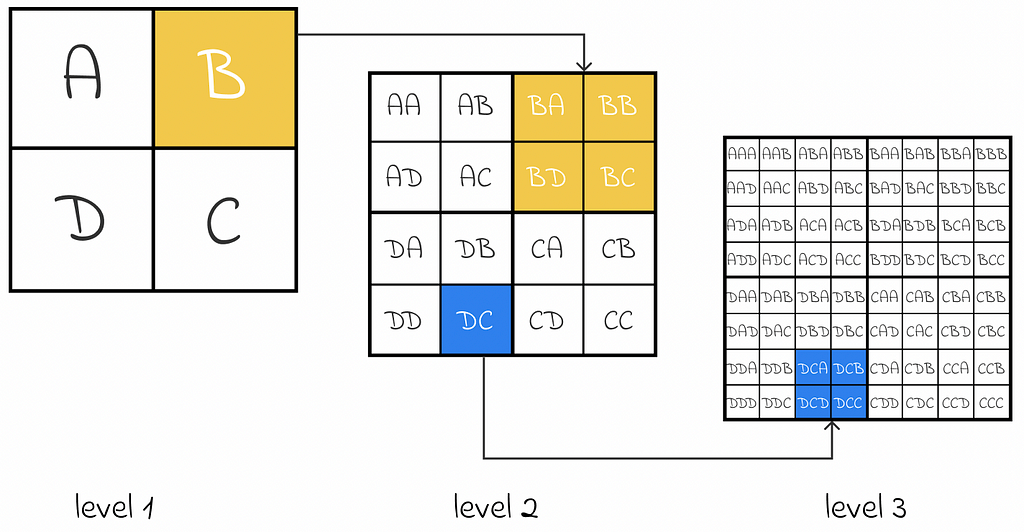
As shown in the picture above, every square on a current level is divided by four equal subsquares in the next level. As a result, encoding a single square on level i requires 2 * i bits.

If a geographical map is divided in this way, then we can encode all of its subparts with a custom number of bits. The more levels are used in the quadtree, the better the precision is.
Properties
Quadtrees are particularly used in geo applications for several advantages:
- Due to its structure, quadtrees allow rapid tree traversal.
- The larger the common prefix of two strings used to encode a pair of points on the map, the closer they are. However, this does not work the other way around in the edge case: a pair of points can be very close to each other but have a small common prefix. Though edge cases occur, they are not that often: they only happen when two small quadrants are located on opposite sides of a border with another much larger quadrant.
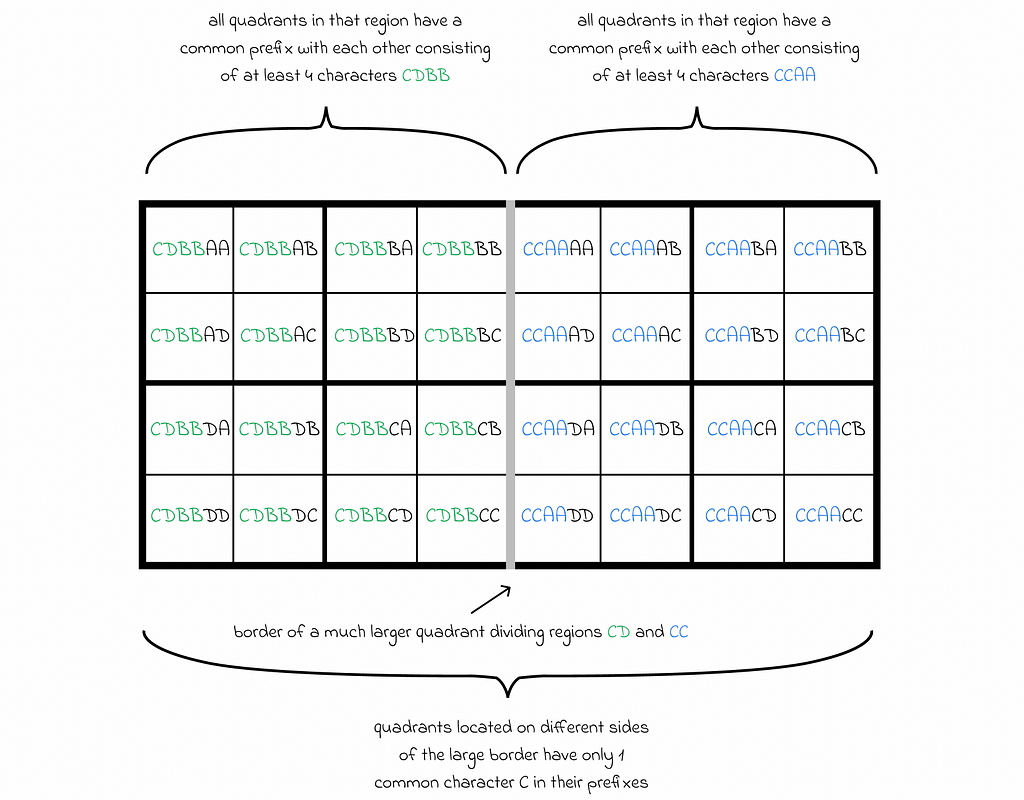
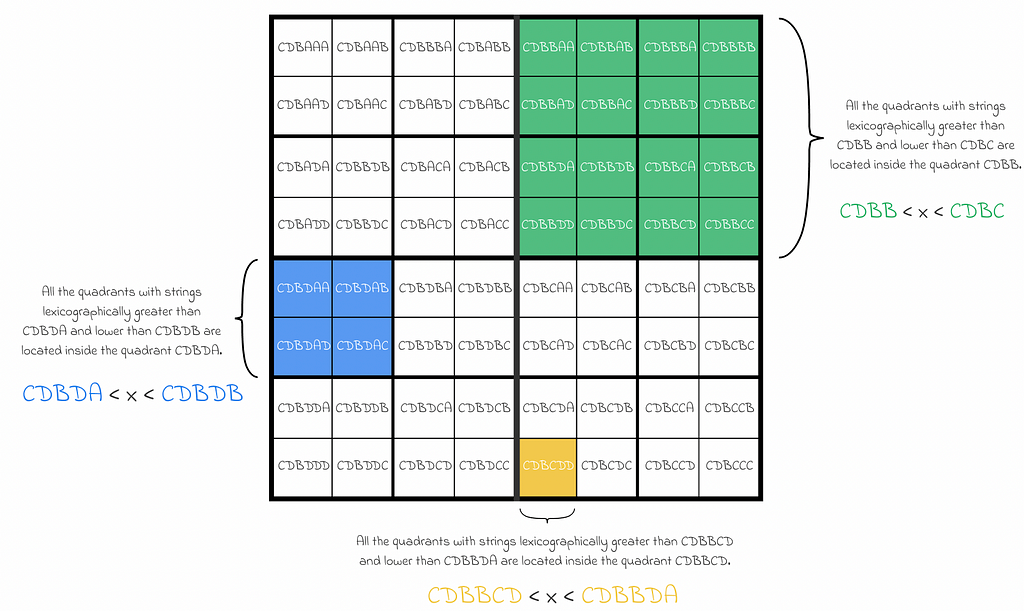
- If a quadrant is represented by a string s₁s₂…sᵢ, then all of the subquadrants it contains, are represented by strings x such as s₁s₂…sᵢ < x < s₁s₂…sⱼ, where sⱼ is the next character after sᵢ in the lexicographical order.
Advantages
The main advantage of quadtrees is that every position on a map is represented by a unique string identifier which can be stored in a database as a single column making it possible to construct an index on quadtree strings. Therefore, given any string representing a region on the map, it becomes very fast:
- to go up to higher levels or to move to lower levels of the region;
- to access all the subregions of the region;
- to find up to all of the 8 adjacent regions on the same level (except for edge cases).
GeoHash
In most real geographical applications, the GeoHash format is used which is a slight modification over the quadtree format:
- instead of squares, geographical regions are divided by rectangles;
- regions are divided into more than four parts;
- every object on the map is encoded by a string in the “base 32” format consisting of digits 0–9 and lowercase letters except “a”, “i”, “l” and “o”.
Despite these slight modifications, GeoHash preserves the important advantages that were described in the section above for quadtrees.
The table below shows the correspondance between every GeoHash level and rectangle sizes. For the large majority of cases, the levels 9 and 10 are already sufficient to give a very precise approximation on the map.

Finding the nearest objects on the map
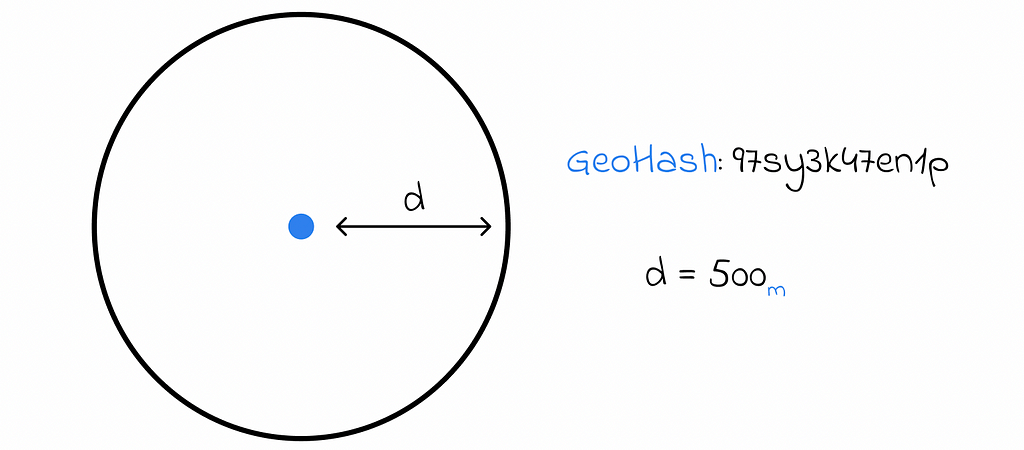
If we have on object on the map, we can find its nearest objects withing a certain distance d by using the following algorithm:
- Converting the object to the GeoHash string s.
2. Finding the first smallest GeoHash level i whose size is greater than the required distance d.
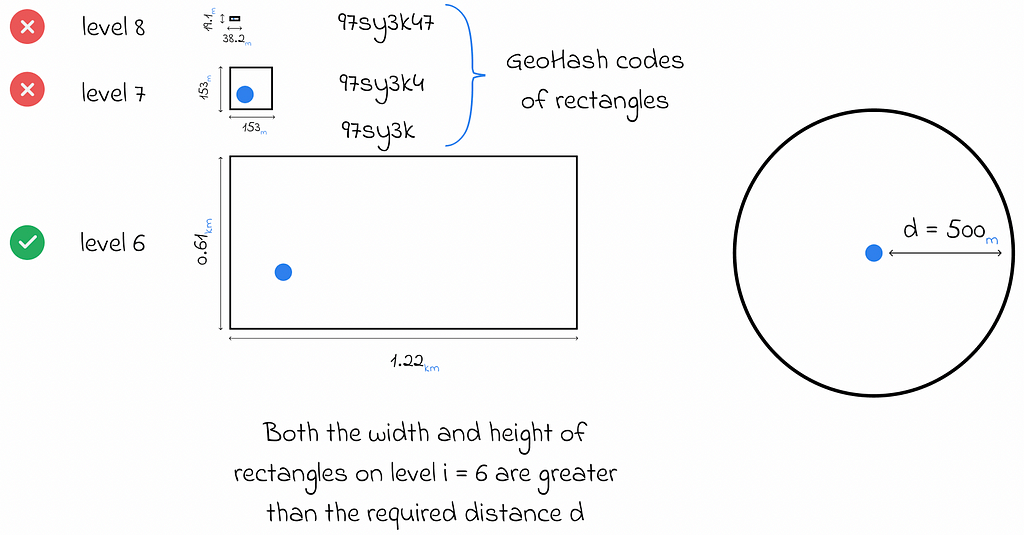
3. Take the first i characters of the string s (to represent the rectangle containing the initial object on level k).
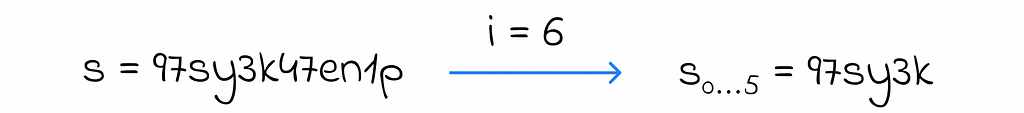
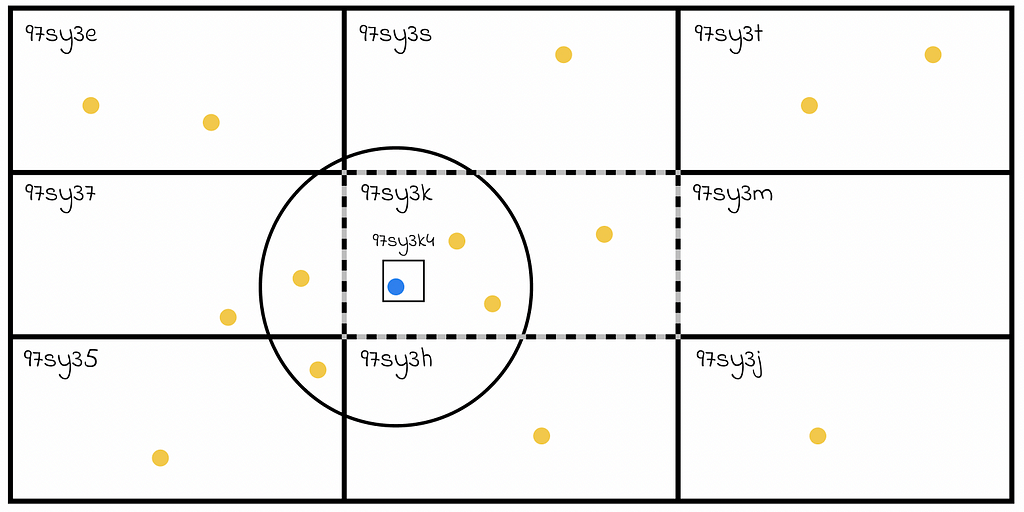
4. Find 8 adjacent regions around the string s[0 … i – 1].
5. Find all the objects in the initial and adjacent regions and filter those objects whose distance to the initial object is less than d.
Conclusion
Fast navigation is a crucial aspect of geoapplications that use data about millions users and places. The key method for achiveing it includes the creation of a single index identifier that can implicitly represent both latitude and longitude.
By inheriting the most important properties of quadtrees, GeoHash server as a great example of such a method that indeed achieves great performance in practice. The only weak side of it is the presence of edge cases when both objects are located on different sides of a large border separating them. Though they might negatively affect the search efficiency, edge cases do not appear that often in practice meaning that GeoHash is still a top choice for geoapplications.
In case if you are familiar with machine learning and would like to learn more about optimized ways to perform scalable similarity search on embeddings, I recommend you go through my other series of articles on it:
Resources
All images unless otherwise noted are by the author.
System Design: Quadtrees & GeoHash was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
