Speaker’s Privacy Protection in DNN-Based Speech Processing Tools

A novel method in privacy-preserving speech processing which anonymizes the speaker attributes using space-filling vector quantization

This post is a short explanation of our proposed privacy preservation technique called Privacy-PORCUPINE [1] published at Interspeech 2024 conference. The post discusses a potential privacy threat that might happen when using ordinary vector quantization in the bottleneck of DNN-based speech processing tools.

Speech is a convenient medium for interacting between humans and with technology, yet evidence demonstrates that it exposes speakers to threats to their privacy. A central issue is that, besides the linguistic content which may be private, speech contains also private side-information such as the speaker’s identity, age, state of health, ethnic background, gender, and emotions. Revealing such sensitive information to a listener may expose the speaker to threats such as price gouging, tracking, harassment, extortion, and identity theft. To protect speakers, privacy-preserving speech processing seeks to anonymize speech signals by stripping away private information that is not required for the downstream task [2].

A common operating principle for privacy-preserving speech processing is to pass information through an information bottleneck that is tight enough to allow only the desired information pass through it and prevent transmission of any other private information. Such bottlenecks can be implemented for example as autoencoders, where a neural network, known as the encoder, compresses information to a bottleneck, and a second network, the decoder, reconstructs the desired output. The information rate of the bottleneck can be quantified absolutely, only if it is quantized, and quantization is thus a required component of any proof of privacy [2]. The figure below shows a vector quantized variational autoencoder (VQ-VAE) architecture, and its bottleneck.

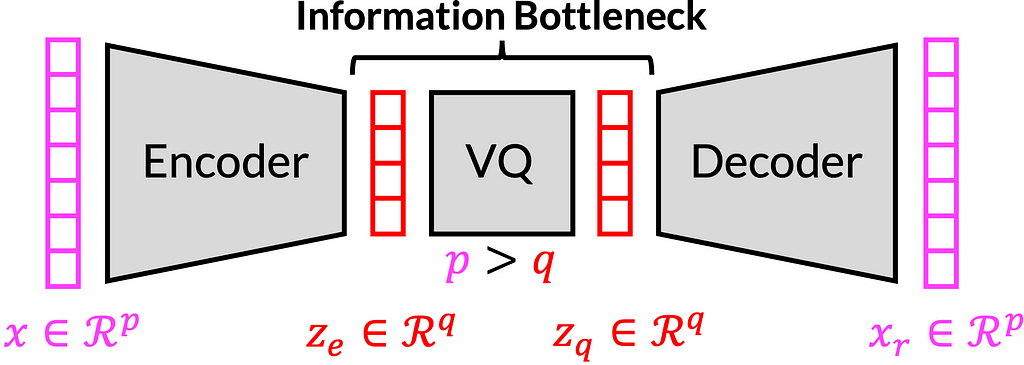
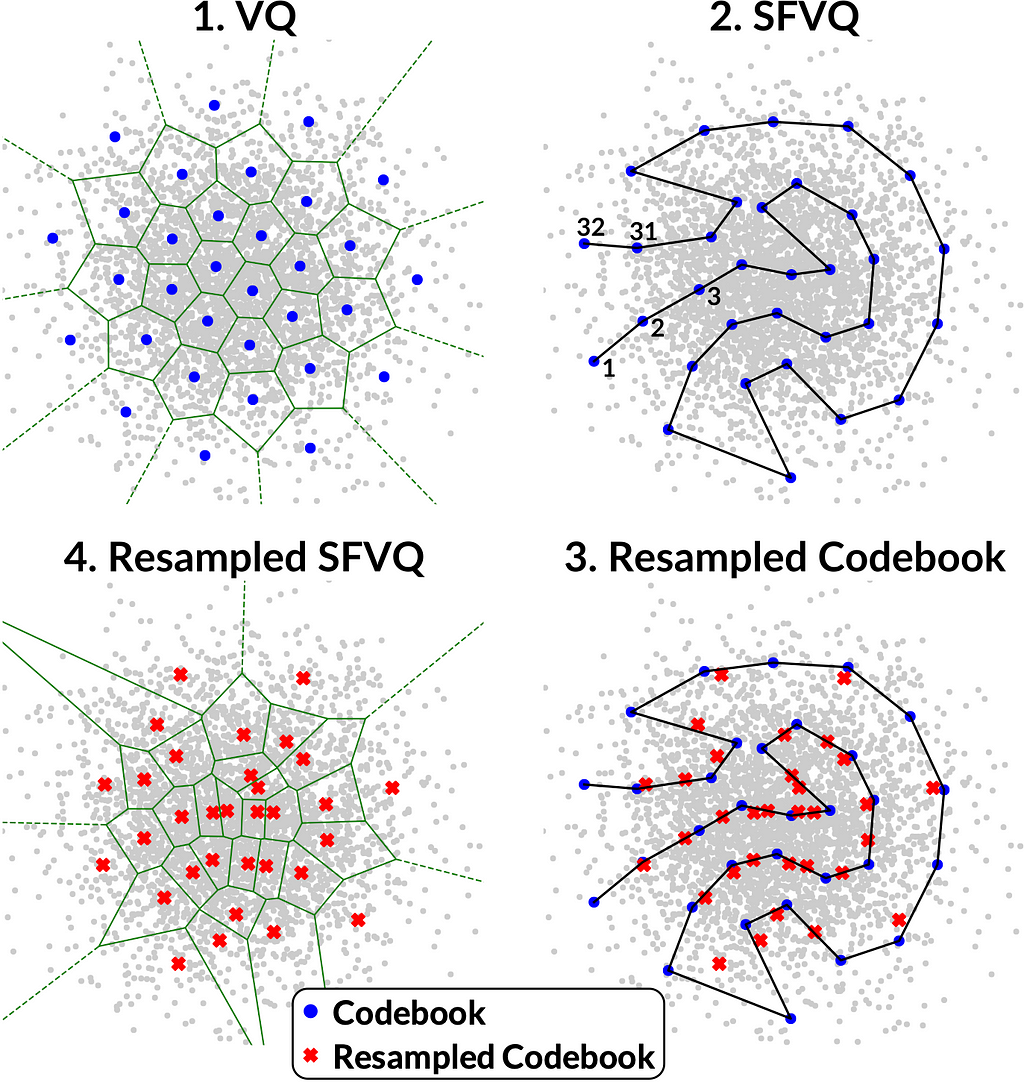
As pointed out in the Privacy ZEBRA framework [3], we need to characterize privacy protections both in terms of average disclosure of private information (in bits) as well as worst-case disclosure (in bits). Vector quantization (VQ) [4] is a constant-bitrate quantizer in the sense that it quantizes the input with a codebook of K elements, and the indices of such a codebook can be expressed with B=log2(K) bits. This B equals to the average disclosure of private information in bits. In terms of the worst-case disclosure, it is obvious that different codebook elements are used with different frequencies (see Fig. 2.1 below). This means that a relatively smaller subset of speakers could be assigned to a particular codebook index, such that any time a speaker is assigned to that codebook index, the range of possible speakers is relatively smaller than for other codebook indices and the corresponding disclosure of private information is larger (for the speakers assigned to this particular codebook index). However, to the best of the authors’ knowledge, this disclosure has not previously been quantified nor do we have prior solutions for compensating for such an increase in disclosure. Hence, our main goal is to modify VQ such that all codebook elements have equal occurrence likelihoods to prevent private information leakage (and thus improve worst-case disclosure).

As a solution, we use here our recently proposed modification of VQ known as space-filling vector quantization (SFVQ) [5], which incorporates space-filling curves into VQ. We define the SFVQ as the linear continuation of VQ, such that subsequent codebook elements are connected with a line where inputs can be mapped to any point on that piece-wise continuous line (see Fig. 2.2). To read more about SFVQ, please see this post.

In our technique, named Privacy PORCUPINE [1], we proposed to use a codebook resampling method together with SFVQ, where a vector quantizer is resampled along the SFVQ’s curve, such that all elements of the resampled codebook have equal occurrence likelihoods (see Fig. 2.3 and 2.4).

How we measure the disclosure?

Figure 2.1 demonstrates that in areas where inputs are less likely, the Voronoi-regions are larger. Hence, such larger Voronoi-regions contain a smaller number of input samples. Similarly, small Voronoi-regions have a larger number of input samples. Such differences are due to the optimization of the codebook by minimizing the mean square error (MSE) criterion; more common inputs are quantized with a smaller error to minimize the average error. Our objective is to determine how such uneven distribution of inputs to codebook entries influences the disclosure of private information.

We measure disclosure in terms of how much the population size of possible identities for an unknown speaker is decreased with a new observation. In other words, assume that we have prior knowledge that the speaker belongs to a population of size M. If we have an observation that the speaker is quantized to an index k, we have to evaluate how many speakers L out of M will be quantized to the same index. This decrease can be quantified by the ratio of populations L/M corresponding to the disclosure of B_leak=log2(M/L) bits of information.

At the extreme, it is possible that only a single speaker may be quantized to a particular index. This means that only one speaker L=1 is quantized to the bin out of an arbitrarily large M, though in practice we can verify results only for finite M. Still, in theory, if M → ∞, then also the disclosure diverges B_leak → ∞ bits. The main objective of our proposed method is to modify vector quantization to prevent such catastrophic leaks.

Codebook Resampling

After training the space-filling vector quantizer (SFVQ) [5] on the training set comprising speaker embeddings for a population of M speakers (Fig. 2.2), we map all the M embedding vectors onto the learned curve. To normalize the occurrence frequency using K codebook vectors, each codebook element has to represent M/K speaker embeddings. In other words, each Voronoi- region should encompass M/K speaker embeddings. Considering these M mapped embeddings on SFVQ’s curve, we start from the first codebook element (one end of the curve), take the first M/K mapped embeddings, and calculate the average of these vectors. We define this average vector as the new resampled codebook vector (red crosses in Fig. 2.3) representing the first chunk of M/K speaker embeddings. Then similarly, we continue until we compute all K resampled codebook vectors for all K chunks of M/K speaker embeddings.

Experiments

In our experiments, we used Common Voice corpus (version 16.1) to get a large pool of speakers. We selected 10,240 speakers randomly for the test set and 79,984 speakers for the train set. To compute speaker embeddings, we used the pretrained speaker verification model of ECAPA-TDNN [6]. We trained vector quantization (VQ) and space-filling vector quantization (SFVQ) methods on the train set (of speaker embeddings) for different bitrates ranging from 4 bit to 10 bit (16 to 1024 codebook vectors).

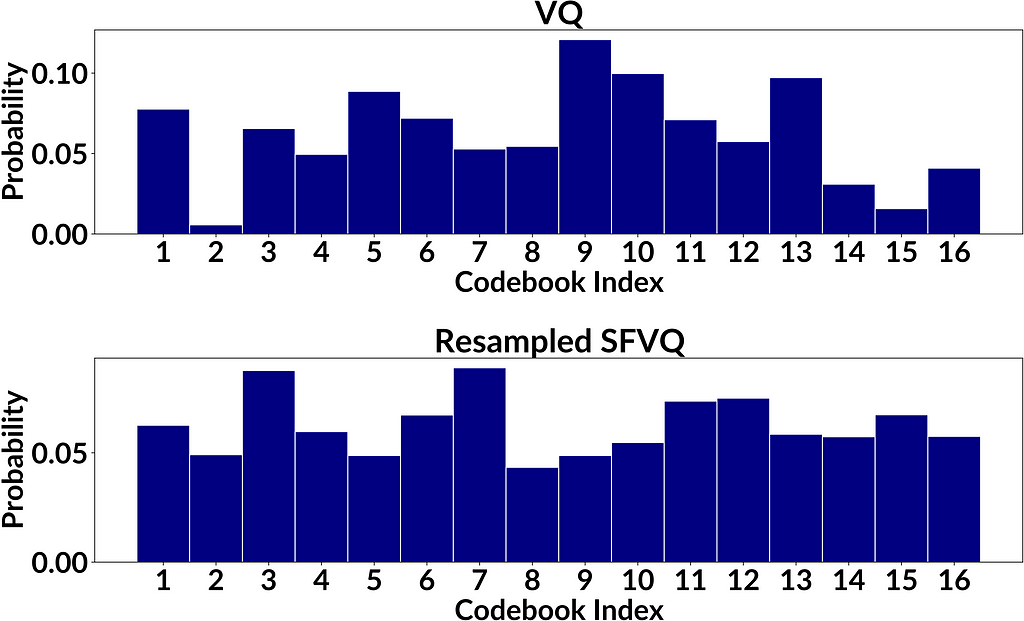
As a showcase to compare VQ and resampled SFVQ, the figure below illustrates the occurrence frequencies for VQ and resampled SFVQ, both with 4 bit of information corresponding to 16 codebook vectors. By informal visual inspection we can see that entries in the proposed method are more uniformly distributed, as desired, but to confirm results we need a proper evaluation. To compare the obtained histograms from VQ and resampled SFVQ, we used different evaluation metrics which are discussed in the next section.

Evaluation Metrics

Suppose we have K codebook vectors (bins) to quantize a population of M speakers. Our target is to achieve a uniform distribution of samples onto the K codebook vectors, U(1,K), such that every codebook vector is used M/K times. If we sample M integers from the uniform distribution of U(1,K), we will obtain the histogram h(k). Then, if we take the histogram of occurrences in the bins of h(k) (i.e. histogram of histogram), we will see that the new histogram follows a binomial distribution f(k) such that

where the random variable X is the occurrence in each bin, n is the number of trials (n=M), and p is the success probability for each trial which is p=1/K. After obtaining the histogram of codebook indices occurrences g(k) (Figure 3) for both VQ and resampled SFVQ methods, we compute the histogram of occurrences in the bins of g(k) denoted by f_hat(k). The binomial distribution f(k) is the theoretical optimum, to which our observation f_hat(k) should coincide. Hence, we use Kullback-Leibler (KL) divergence between f(k) and f_hat(k) to assess the distance between the observed and the ideal distributions.

By having the histogram of occurrences g(k), we calculate the minimum of the histogram divided by the total number of samples (M=Σ g(k)) as the worst-case disclosure. We also compute the average disclosure as entropy of occurrence frequencies g(k)/M. In addition, we use a sparseness measure and standard deviation as heuristic measures of uniformity of the obtained histogram g(k). Here are the evaluation formulas:

Results

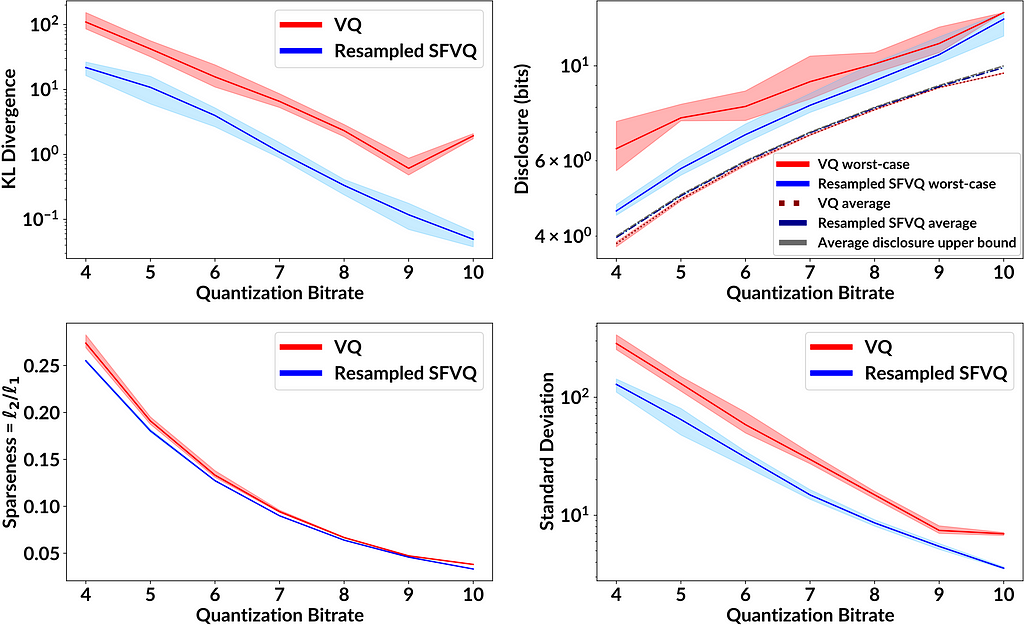
Figure 4 shows the performance of VQ and resampled SFVQ as a function of bitrate. In each case and for all bitrates, the proposed method (blue line) is below VQ (red line), indicating that the leakage of private information is smaller for the proposed method. One important point to mention is that as expected, resampled SFVQ makes the average disclosure to be slightly higher than VQ, whereas the average disclosure for both resampled SFVQ and VQ are extremely close to the upper bound of average disclosure where the histogram of occurrence frequencies is perfectly flat.

Conclusions

Privacy-preserving speech processing is becoming increasingly important as the usage of speech technology is increasing. By removing superfluous private information from a speech signal by passing it through a quantized information bottleneck, we can gain provable protections for privacy. Such protections however rely on the assumption that quantization levels are used with equal frequency. Our theoretical analysis and experiments demonstrate that vector quantization, optimized with the minimum mean square (MSE) criterion, does generally not provide such uniform occurrence frequencies. In the worst case, some speakers could be uniquely identified even if the quantizer on average provides ample protection.

We proposed the resampled SFVQ method to avoid such privacy threats. The protection of privacy is thus achieved by increasing the quantization error for inputs that occur less frequently, while more common inputs gain better accuracy (see Fig. 2.4). This is in line with the theory of differential privacy [7].

We used speaker identification as an illustrative application, though the proposed method can be used in gaining a provable reduction of private information leakage for any attributes of speech. In summary, resampled SFVQ is a generic tool for privacy-preserving speech processing. It provides a method for quantifying the amount of information passing through an information bottleneck and thus forms the basis of speech processing methods with provable privacy.

GitHub Repository

The code for implementation of our proposed method and the relevant evaluations is publicly available in the following link:

GitHub – MHVali/Privacy-PORCUPINE

Acknowledgement

Special thanks to my doctoral program supervisor Prof. Tom Bäckström, who supported me and was the other contributor for this work.

References

[1] M.H. Vali, T. Bäckström, “Privacy PORCUPINE: Anonymization of Speaker Attributes Using Occurrence Normalization for Space-Filling Vector Quantization”, in Proceedings of Interspeech, 2024.

[2] T. Bäckström, “Privacy in speech technology”, 2024. [Online] Available at: https://arxiv.org/abs/2305.05227

[3] A. Nautsch et. al. , “The Privacy ZEBRA: Zero Evidence Biometric Recognition Assessment,” in Proceedings of Interspeech, 2020.

[4] M. H. Vali and T. Bäckström, “NSVQ: Noise Substitution in Vector Quantization for Machine Learning,” IEEE Access, 2022.

[5] M.H. Vali, T. Bäckström, “Interpretable Latent Space Using Space-Filling Curves for Phonetic Analysis in Voice Conversion”, in Proceedings of Interspeech, 2023.

[6] B. Desplanques, J. Thienpondt, and K. Demuynck, “ECAPA-TDNN: Emphasized Channel Attention, Propagation and Aggregation in TDNN Based Speaker Verification,” in Proceedings of Interspeech, 2020.

[7] C. Dwork, “Differential privacy: A survey of results,” in
International conference on theory and applications of models
of computation. Springer, 2008.

Speaker’s Privacy Protection in DNN-Based Speech Processing Tools was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.