Perception-Inspired Graph Convolution for Music Understanding Tasks

This article discusses MusGConv, a perception-inspired graph convolution block for symbolic musical applications

Introduction

In the field of Music Information Research (MIR), the challenge of understanding and processing musical scores has continuously been introduced to new methods and approaches. Most recently many graph-based techniques have been proposed as a way to target music understanding tasks such as voice separation, cadence detection, composer classification, and Roman numeral analysis.

This blog post covers one of my recent papers in which I introduced a new graph convolutional block, called MusGConv, designed specifically for processing music score data. MusGConv takes advantage of music perceptual principles to improve the efficiency and the performance of graph convolution in Graph Neural Networks applied to music understanding tasks.

Understanding the Problem

Traditional approaches in MIR often rely on audio or symbolic representations of music. While audio captures the intensity of sound waves over time, symbolic representations like MIDI files or musical scores encode discrete musical events. Symbolic representations are particularly valuable as they provide higher-level information essential for tasks such as music analysis and generation.

However, existing techniques based on symbolic music representations often borrow from computer vision (CV) or natural language processing (NLP) methodologies. For instance, representing music as a “pianoroll” in a matrix format and treating it similarly to an image, or, representing music as a series of tokens and treating it with sequential models or transformers. These approaches, though effective, could fall short in fully capturing the complex, multi-dimensional nature of music, which includes hierarchical note relation and intricate pitch-temporal relationships. Some recent approaches have been proposed to model the musical score as a graph and apply Graph Neural Networks to solve various tasks.

The Musical Score as a Graph

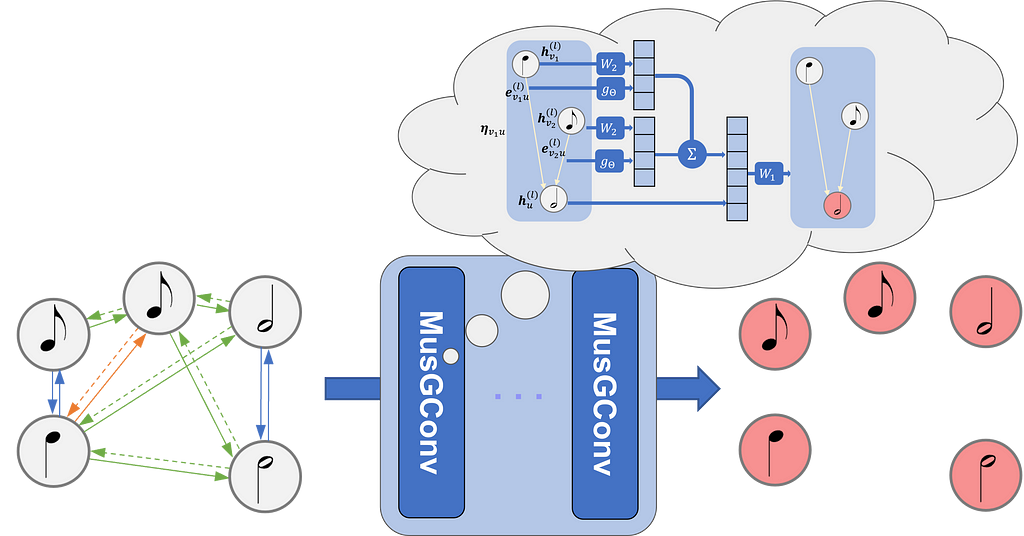
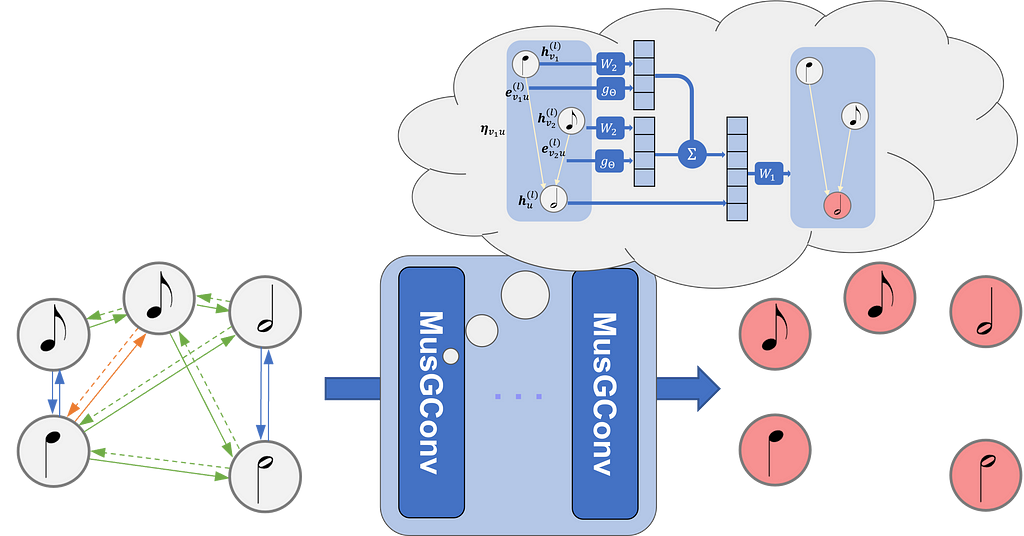
The fundamental idea of GNN-based approaches to musical scores is to model a musical score as a graph where notes are the vertices and edges are built from the temporal relations between the notes. To create a graph from a musical score we can consider four types of edges (see Figure below for a visualization of the graph on the score):

• onset edges: connect notes that share the same onset;
• consecutive edges (or next edges): connect a note x to a note y if the offset of x corresponds to the onset of y;
• during edges: connect a note x to a note y if the onset of y falls within the onset and offset of x;
• rest edges (or silence edges): connect the last notes before a rest to the first ones after it.

A GNN can treat the graph created from the notes and these four types of relations.

Introducing MusGConv

MusGConv is designed to leverage music score graphs and enhance them by incorporating principles of music perception into the graph convolution process. It focuses on two fundamental dimensions of music: pitch and rhythm, considering both their relative and absolute representations.

Absolute representations refer to features that can be attributed to each note individually such as the note’s pitch or spelling, its duration or any other feature. On the other hand, relative features are computed between pairs of notes, such as the music interval between two notes, their onset difference, i.e. the time on which they occur, etc.

Key Features of MusGConv

1. Edge Feature Computation: MusGConv computes edge features based on the distances between notes in terms of onset, duration, and pitch. The edge features can be normalized to ensure they are more effective for Neural Network computations.
2. Relative and Absolute Representations: By considering both relative features (distance between pitches as edge features) and absolute values (actual pitch and timing as node features), MusGConv can adapt and use the representation that is more relevant depending on the occasion.
3. Integration with Graph Neural Networks: The MusGConv block integrates easily with existing GNN architectures with almost no additional computational cost and can be used to improve musical understanding tasks such as voice separation, harmonic analysis, cadence detection, or composer identification.

The importance and coexistence of the relative and absolute representations can be understood from a transpositional perspective in music. Imagine the same music content transposed. Then, the intervalic relations between notes stay the same but the pitch of each note is altered.

Understanding Message Passing in Graph Neural Networks (GNNs)

To fully understand the inner workings of the MusGConv convolution block it is important to first explain the principles of Message Passing.

What is Message Passing?

In the context of GNNs, message passing is a process where vertices within a graph exchange information with their neighbors to update their own representations. This exchange allows each node to gather contextual information from the graph, which is then used to for predictive tasks.

The message passing process is defined by the following steps:

1. Initialization: Each node is assigned to a feature vector, which can include some important properties. For example in a musical score, this could include pitch, duration, and onset time for each node/note.
2. Message Generation: Each node generates a message to send to its neighbors. The message typically includes the node’s current feature vector and any edge features that describe the relationship between the nodes. A message can be for example a linear transformation of the neighbor’s node features.
3. Message Aggregation: Each node collects messages from its neighbors. The aggregation function is usually a permutation invariant function such as sum, mean, or max and it combines these messages into a single vector, ensuring that the node captures information from its entire neighborhood.
4. Node Update: The aggregated message is used to update the node’s feature vector. This update often involves applying a neural network layer (like a fully connected layer) followed by a non-linear activation function (such as ReLU).
5. Iteration: Steps 2–4 are repeated for a specified number of iterations or layers, allowing information to propagate through the graph. With each iteration, nodes incorporate information from progressively larger neighborhoods.

Message Passing in MusGConv

MusGConv alters the standard message passing process mainly by incorporating both absolute features as node features and relative musical features as edge features. This design is tailored to fit the nature of musical data.

The MusGConv convolution is defined by the following steps:

1. Edge Features Computation: In MusGConv, edge features are computed as the difference between notes in terms of onset, duration, and pitch. Additionally, pitch-class intervals (distances between notes without considering the octave) are included, providing an reductive but effective method to quantify music intervals.
2. Message Computation: The message within the MusGConv includes the source node’s current feature vector but also the afformentioned edge features from the source to the destination node, allowing the network to leverage both absolute and relative information of the neighbors during message passing.
3. Aggregation and Update: MusGConv uses sum as the aggregation function, however, it concatenates the current node representation with the sum of its neighbor messages.

By designing the message passing mechanism in this way, MusGConv attempts to preserve the relative perceptual properties of music (such as intervals and rhythms), leading to more meaningful representations of musical data.

Should edge features are absent or deliberately not provided then MusGConv computes the edge features between two nodes as the absolute difference between their node features. The version of MusGConv with the edges features is named MusGConv(+EF) in the experiments.

Applications and Experiments

To demonstrate the potential of MusGConv I discuss below the tasks and the experiments conducted in the paper. All models independent of the task are designed with the pipeline shown in the figure below. When MusGConv is employed the GNN blocks are replaced by MusGConv blocks.

I decided to apply MusGConv to four tasks: voice separation, composer classification, Roman numeral analysis, and cadence detection. Each one of these tasks presents a different taxonomy from a graph learning perspective. Voice separation is a link prediction task, composer classification is a global classification task, cadence detection is a node classification task, and Roman numeral analysis can be viewed as a subgraph classification task. Therefore we are exploring the suitability of MusGConv not only from a musical analysis perspective but through out the spectrum of graph deep learning task taxonomy.

Voice Separation

Voice separation is the detection of individual monophonic streams within a polyphonic music excerpt. Previous methods had employed GNNs to solve this task. From a GNN perspective, voice separation can be viewed as link prediction task, i.e. for every pair of notes we predict if they are connected by an edge or not. The product the link prediction process should be a graph where consecutive notes in the same voice are ought to be connected. Then voices are the connected components of the predicted graph. I point the readers to this paper for more information on voice separation using GNNs.

For voice separation the pipeline of the above figure applies to the GNN encoder part of the architecture. The link prediction part takes place as the task specific module of the pipeline. To use MusGConv it is sufficient to replace the convolution blocks of the GNN encoder with MusGConv. This simple substitution results in more accurate prediction making less mistakes.

Since the interpretation of deep learning systems is not exactly trivial, it is not easy to pinpoint the reason for the improved performance. From a musical perspective consecutive notes in the same voice should tend to have smaller relative pitch difference. The design of MusGConv definitely outlines the pitch differences with the relative edge features. However, I would need to also say, from individual observations that music does not strictly follow any rules.

Composer Classification

Composer classification is the process of identifying a composer based on some music excerpt. Previous GNN-based approaches for this task receive a score graph as input similarly to the pipeline shown above and then they include some global pooling layer that collapses the graph of the music excerpt to a vector. From that vector then the classification process applied where classes are the predefined composers.

Yet again, MusGConv is easy to implement by replacing the GNN convolutional blocks. In the experiments, using MusGConv was indeed very beneficial in solving this task. My intuition is that relative features in combination with the absolute give better insights to compositional style.

Roman Numeral Analysis

Roman numeral analysis is a method for harmonic analysis where chords are represented as Roman numerals. The task for predicting the Roman numerals is a fairly complex one. Previous architectures used a mixture of GNNs and Sequential models. Additionally, Roman numeral analysis is a multi-task classification problem, typically a Roman numeral is broken down to individual simpler tasks in order to reduce the class vocabulary of unique Roman numerals. Finally, the graph-based architecture of Roman numeral analysis also includes a onset contraction layer after the graph convolution that transforms the graph to an ordered sequence. This onset contraction layer, contracts groups of notes that occur at the same time and they are assigned to the same label during classification. Therefore, it can be viewed as a subgraph classification task. I would reckon that the explication of this model would merit its own post, therefore, I would suggest reading the paper for more insights.

Nevertheless, the general graph pipeline in the figure is still applicable. The sequential models together with the multitask classification process and the onset contraction module entirely belong to the task-specific box. However, replacing the Graph Convolutional Blocks with MusGConv blocks does not seem to have an effect on this task and architecture. I attribute this to the fact that the task and the model architecture are simply too complex.

Cadence Detection

Finally, let’s discuss cadence detection. Detecting cadences can be viewed as similar to detecting phrase endings and it is an important aspect of music analysis. Previous methods for cadence detection employed GNNs with an encoder-decoder GNN architecture. Each note which by now we know that also corresponds to one node in the graph is classified to being a cadence note or not. The cadence detection task includes a lot of peculiarities such as very heavy class imbalances as well as annotation ambiguities. If you are interested I would again suggest to check out this paper.

The use of MusGConv convolution in the encoder of can be beneficial for detecting cadences. I believe that the combination of relative and absolute features and the design of MusGConv can keep track of voice leading patterns that often occur around cadences.

Results and Evaluation

Extensive experiments have shown that MusGConv can outperform state-of-the-art models across the aforementioned music understanding tasks. The table below summarizes the improvements:

However soulless a table can be, I would prefer not to fully get into any more details in the spirit of keeping this blog post lively and towards a discussion. Therefore, I invite you to check out the original paper for more details on the results and datasets.

Summary and Discussion

MusGConv is a graph convolutional block for music. It offers a simple perception-inspired approach to graph convolution that results to performance improvement of GNNs when applied to music understanding tasks. Its simplicity is the key to its effectiveness. In some tasks, it is very beneficial is some others not so much. The inductive bias of the relative and absolute features in music is a neat trick to magically improve your GNN results but my advice is to always take it with a pinch of salt. Try out MusGConv by all means but also do not forget about all the other cool graph convolutional block possibilities.

If you are interested in trying MusGConv, the code and models are available on GitHub.

Notes and Acknowledgments

All images in this post are by the author. I would like to thank Francesco Foscarin my co-author of the original paper for his contributions to this work.

Perception-Inspired Graph Convolution for Music Understanding Tasks was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.