Originally appeared here:
XRP to reach $7.50 in the next 45 days while this $0.150 altcoin looks to breach $10
Blog
-
XRP to reach $7.50 in the next 45 days while this $0.150 altcoin looks to breach $10
Ripple targets $7.50 while Rexas Finance, a $0.15 altcoin, eyes a 67x rise to $10, setting the stage for a thrilling crypto showdown. #partnercontent -
Bitget sets to innovate gas payments with BGB token amid major 40% supply burn
Bitget Wallet will prioritize its native BGB token for multi-chain gas payments via its innovative GetGas feature starting January 2025, according to a Dec. 27 statement shared with CryptoSlate. This initiative is set to streamline operations across multiple blockchains, including Ethereum, Solana, BNB Chain, Polygon, Base, Arbitrum, Optimism, TON, and Tron. According to the firm, […]
The post Bitget sets to innovate gas payments with BGB token amid major 40% supply burn appeared first on CryptoSlate.
Originally appeared here:
Bitget sets to innovate gas payments with BGB token amid major 40% supply burn -
Treasury and IRS finish broker rules for DeFi, require KYC from protocols
The US Department of the Treasury and the Internal Revenue Service (IRS) have released the final version of its broker rules to digital assets services providers, which includes provisions on requiring DeFi protocols to conduct Know-Your-Customer (KYC) procedures. Industry experts have already criticized the new provision for being unlawful and out of the Treasury’s regulatory […]
The post Treasury and IRS finish broker rules for DeFi, require KYC from protocols appeared first on CryptoSlate.
Go here to Read this Fast! Treasury and IRS finish broker rules for DeFi, require KYC from protocols
Originally appeared here:
Treasury and IRS finish broker rules for DeFi, require KYC from protocols -
Bitwise’s ‘Bitcoin company’ ETF could set the trend for 2025 – Details
Bitcoin’s Spot ETF segment is heating up, with Bitwise’s latest application the most recent example
Post-festive season flows look to be adopting a positive shift after recent ETF outflowsThe post Bitwise’s ‘Bitcoin company’ ETF could set the trend for 2025 – Details appeared first on AMBCrypto.
Bitwise’s ‘Bitcoin company’ ETF could set the trend for 2025 – DetailsBitwise’s ‘Bitcoin company’ ETF could set the trend for 2025 – Details -
Bitcoin, Ethereum, and Dogecoin plummet after Christmas – Is this the new trend?
Bitcoin and Ethereum netflows pictured similar patterns around Christmas
Open Interest trends revealed wary sentiment among tradersBitcoin [BTC] tends to see a Santa Claus rally in the week
The post Bitcoin, Ethereum, and Dogecoin plummet after Christmas – Is this the new trend? appeared first on AMBCrypto.
Originally appeared here:
Bitcoin, Ethereum, and Dogecoin plummet after Christmas – Is this the new trend? -
Here’s the case for THETA going on a 37% price rally
At press time, 69.2% of top traders on Binance held long positions in THETA
THETA’s Relative Strength Index (RSI) stood at 43, indicating a potential for upside momentumTHETA, the native
The post Here’s the case for THETA going on a 37% price rally appeared first on AMBCrypto.
Here’s the case for THETA going on a 37% price rallyHere’s the case for THETA going on a 37% price rally -

Building Trust in LLM Answers: Highlighting Source Texts in PDFs

100% accuracy isn’t everything: helping users navigate the document is the real value
Originally appeared here:
Building Trust in LLM Answers: Highlighting Source Texts in PDFsGo Here to Read this Fast! Building Trust in LLM Answers: Highlighting Source Texts in PDFs
-
Introduction to the Finite Normal Mixtures in Regression with
Introduction to the Finite Normal Mixtures in Regression with R
How to make linear regression flexible enough for non-linear data
The linear regression is usually considered not flexible enough to tackle the nonlinear data. From theoretical viewpoint it is not capable to dealing with them. However, we can make it work for us with any dataset by using finite normal mixtures in a regression model. This way it becomes a very powerful machine learning tool which can be applied to virtually any dataset, even highly non-normal with non-linear dependencies across the variables.
What makes this approach particularly interesting comes with interpretability. Despite an extremely high level of flexibility all the detected relations can be directly interpreted. The model is as general as neural network, still it does not become a black-box. You can read the relations and understand the impact of individual variables.
In this post, we demonstrate how to simulate a finite mixture model for regression using Markov Chain Monte Carlo (MCMC) sampling. We will generate data with multiple components (groups) and fit a mixture model to recover these components using Bayesian inference. This process involves regression models and mixture models, combining them with MCMC techniques for parameter estimation.

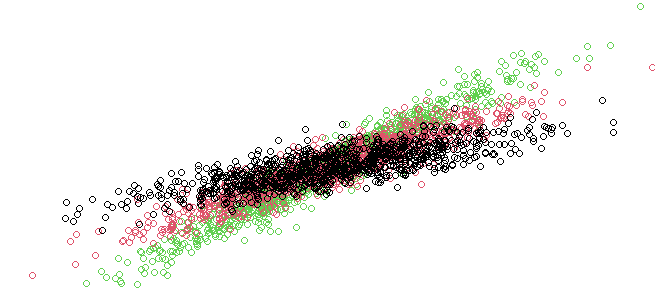
Data simulated as a mixtures of three linear regressions Loading Required Libraries
We begin by loading the necessary libraries to work with regression models, MCMC, and multivariate distributions
# Loading the required libraries for various functions
library("pscl") # For pscl specific functions, like regression models
library("MCMCpack") # For MCMC sampling functions, including posterior distributions
library(mvtnorm) # For multivariate normal distribution functio- pscl: Used for various statistical functions like regression models.
- MCMCpack: Contains functions for Bayesian inference, particularly MCMC sampling.
- mvtnorm: Provides tools for working with multivariate normal distributions.
Data Generation
We simulate a dataset where each observation belongs to one of several groups (components of the mixture model), and the response variable is generated using a regression model with random coefficients.
We consider a general setup for a regression model using G Normal mixture components.
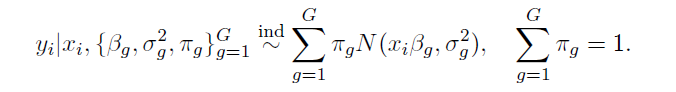
## Generate the observations
# Set the length of the time series (number of observations per group)
N <- 1000
# Set the number of simulations (iterations of the MCMC process)
nSim <- 200
# Set the number of components in the mixture model (G is the number of groups)
G <- 3- N: The number of observations per group.
- nSim: The number of MCMC iterations.
- G: The number of components (groups) in our mixture model.
Simulating Data
Each group is modeled using a univariate regression model, where the explanatory variables (X) and the response variable (y) are simulated from normal distributions. The betas represent the regression coefficients for each group, and sigmas represent the variance for each group.
# Set the values for the regression coefficients (betas) for each group
betas <- 1:sum(dimG) * 2.5 # Generating sequential betas with a multiplier of 2.5
# Define the variance (sigma) for each component (group) in the mixture
sigmas <- rep(1, G) / 1 # Set variance to 1 for each component, with a fixed divisor of 1- betas: These are the regression coefficients. Each group’s coefficient is sequentially assigned.
- sigmas: Represents the variance for each group in the mixture model.
In this model we allow each mixture component to possess its own variance paraameter and set of regression parameters.
Group Assignment and Mixing
We then simulate the group assignment of each observation using a random assignment and mix the data for all components.
We augment the model with a set of component label vectors for
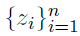
where
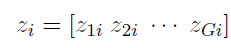
and thus z_gi=1 implies that the i-th individual is drawn from the g-th component of the mixture.
This random assignment forms the z_original vector, representing the true group each observation belongs to.
# Initialize the original group assignments (z_original)
z_original <- matrix(NA, N * G, 1)
# Repeat each group label N times (assign labels to each observation per group)
z_original <- rep(1:G, rep(N, G))
# Resample the data rows by random order
sampled_order <- sample(nrow(data))
# Apply the resampled order to the data
data <- data[sampled_order,]Bayesian Inference: Priors and Initialization
We set prior distributions for the regression coefficients and variances. These priors will guide our Bayesian estimation.
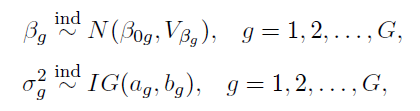
## Define Priors for Bayesian estimation# Define the prior mean (muBeta) for the regression coefficients
muBeta <- matrix(0, G, 1)# Define the prior variance (VBeta) for the regression coefficients
VBeta <- 100 * diag(G) # Large variance (100) as a prior for the beta coefficients# Prior for the sigma parameters (variance of each component)
ag <- 3 # Shape parameter
bg <- 1/2 # Rate parameter for the prior on sigma
shSigma <- ag
raSigma <- bg^(-1)- muBeta: The prior mean for the regression coefficients. We set it to 0 for all components.
- VBeta: The prior variance, which is large (100) to allow flexibility in the coefficients.
- shSigma and raSigma: Shape and rate parameters for the prior on the variance (sigma) of each group.
For the component indicators and component probabilities we consider following prior assignment
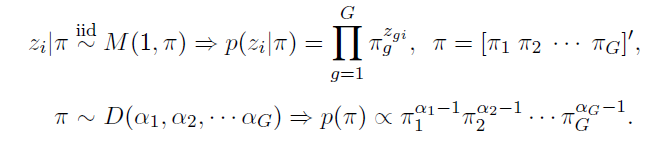
The multinomial prior M is the multivariate generalizations of the binomial, and the Dirichlet prior D is a multivariate generalization of the beta distribution.
MCMC Initialization
In this section, we initialize the MCMC process by setting up matrices to store the samples of the regression coefficients, variances, and mixing proportions.
## Initialize MCMC sampling# Initialize matrix to store the samples for beta
mBeta <- matrix(NA, nSim, G)# Assign the first value of beta using a random normal distribution
for (g in 1:G) {
mBeta[1, g] <- rnorm(1, muBeta[g, 1], VBeta[g, g])
}# Initialize the sigma^2 values (variance for each component)
mSigma2 <- matrix(NA, nSim, G)
mSigma2[1, ] <- rigamma(1, shSigma, raSigma)# Initialize the mixing proportions (pi), using a Dirichlet distribution
mPi <- matrix(NA, nSim, G)
alphaPrior <- rep(N/G, G) # Prior for the mixing proportions, uniform across groups
mPi[1, ] <- rdirichlet(1, alphaPrior)- mBeta: Matrix to store samples of the regression coefficients.
- mSigma2: Matrix to store the variances (sigma squared) for each component.
- mPi: Matrix to store the mixing proportions, initialized using a Dirichlet distribution.
MCMC Sampling: Posterior Updates
If we condition on the values of the component indicator variables z, the conditional likelihood can be expressed as
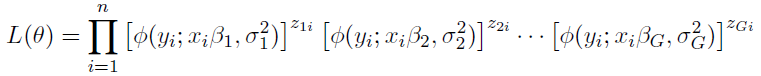
In the MCMC sampling loop, we update the group assignments (z), regression coefficients (beta), and variances (sigma) based on the posterior distributions. The likelihood of each group assignment is calculated, and the group with the highest posterior probability is selected.
The following complete posterior conditionals can be obtained:
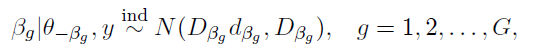
where
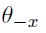
denotes all the parameters in our posterior other than x.
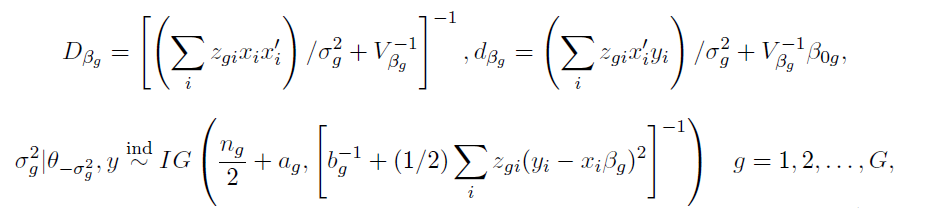
and where n_g denotes the number of observations in the g-th component of the mixture.
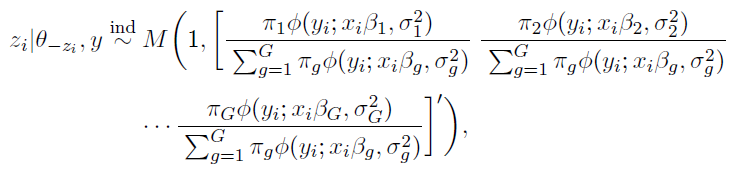
and
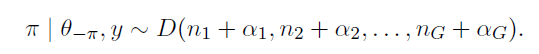
Algorithm below draws from the series of posterior distributions above in a sequential order.
## Start the MCMC iterations for posterior sampling# Loop over the number of simulations
for (i in 2:nSim) {
print(i) # Print the current iteration number
# For each observation, update the group assignment (z)
for (t in 1:(N*G)) {
fig <- NULL
for (g in 1:G) {
# Calculate the likelihood of each group and the corresponding posterior probability
fig[g] <- dnorm(y[t, 1], X[t, ] %*% mBeta[i-1, g], sqrt(mSigma2[i-1, g])) * mPi[i-1, g]
}
# Avoid zero likelihood and adjust it
if (all(fig) == 0) {
fig <- fig + 1/G
}
# Sample a new group assignment based on the posterior probabilities
z[i, t] <- which(rmultinom(1, 1, fig/sum(fig)) == 1)
}
# Update the regression coefficients for each group
for (g in 1:G) {
# Compute the posterior mean and variance for beta (using the data for group g)
DBeta <- solve(t(X[z[i, ] == g, ]) %*% X[z[i, ] == g, ] / mSigma2[i-1, g] + solve(VBeta[g, g]))
dBeta <- t(X[z[i, ] == g, ]) %*% y[z[i, ] == g, 1] / mSigma2[i-1, g] + solve(VBeta[g, g]) %*% muBeta[g, 1]
# Sample a new value for beta from the multivariate normal distribution
mBeta[i, g] <- rmvnorm(1, DBeta %*% dBeta, DBeta)
# Update the number of observations in group g
ng[i, g] <- sum(z[i, ] == g)
# Update the variance (sigma^2) for each group
mSigma2[i, g] <- rigamma(1, ng[i, g]/2 + shSigma, raSigma + 1/2 * sum((y[z[i, ] == g, 1] - (X[z[i, ] == g, ] * mBeta[i, g]))^2))
}
# Reorder the group labels to maintain consistency
reorderWay <- order(mBeta[i, ])
mBeta[i, ] <- mBeta[i, reorderWay]
ng[i, ] <- ng[i, reorderWay]
mSigma2[i, ] <- mSigma2[i, reorderWay]
# Update the mixing proportions (pi) based on the number of observations in each group
mPi[i, ] <- rdirichlet(1, alphaPrior + ng[i, ])
}This block of code performs the key steps in MCMC:
- Group Assignment Update: For each observation, we calculate the likelihood of the data belonging to each group and update the group assignment accordingly.
- Regression Coefficient Update: The regression coefficients for each group are updated using the posterior mean and variance, which are calculated based on the observed data.
- Variance Update: The variance of the response variable for each group is updated using the inverse gamma distribution.
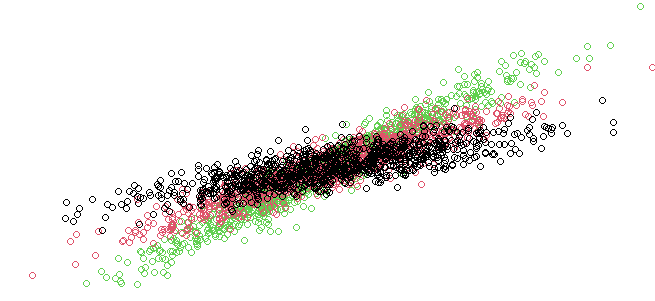
Visualizing the Results
Finally, we visualize the results of the MCMC sampling. We plot the posterior distributions for each regression coefficient, compare them to the true values, and plot the most likely group assignments.
# Plot the posterior distributions for each beta coefficient
par(mfrow=c(G,1))
for (g in 1:G) {
plot(density(mBeta[5:nSim, g]), main = 'True parameter (vertical) and the distribution of the samples') # Plot the density for the beta estimates
abline(v = betas[g]) # Add a vertical line at the true value of beta for comparison
}This plot shows how the MCMC samples (posterior distribution) for the regression coefficients converge to the true values (betas).
Conclusion
Through this process, we demonstrated how finite normal mixtures can be used in a regression context, combined with MCMC for parameter estimation. By simulating data with known groupings and recovering the parameters through Bayesian inference, we can assess how well our model captures the underlying structure of the data.
Unless otherwise noted, all images are by the author.
Introduction to the Finite Normal Mixtures in Regression with was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Introduction to the Finite Normal Mixtures in Regression withGo Here to Read this Fast! Introduction to the Finite Normal Mixtures in Regression with
-
Save $70 on Apple’s 256GB iPad mini 7 during today’s flash sale
 The lowest price on Apple’s iPad mini 7 can be found at B&H and Amazon, with both retailers running a limited-time deal on the 256GB model.
The lowest price on Apple’s iPad mini 7 can be found at B&H and Amazon, with both retailers running a limited-time deal on the 256GB model.
Save $70 on Apple’s iPad mini 7 with 256GB capacity.The 256GB iPad mini 7 in Space Gray can be snapped up for $529 at B&H and Amazon today, with both retailers knocking $70 off Apple’s MSRP on the Wi-Fi model.
Save $70 on Apple’s 256GB iPad mini 7 during today’s flash saleSave $70 on Apple’s 256GB iPad mini 7 during today’s flash sale -

How we work: Charles prepares for a big Apple tech refresh in 2025
 Charles really loves his mostly-older Apple gear, but 2025 is going to be a year of change. Here’s how he gets work done at AppleInsider.
Charles really loves his mostly-older Apple gear, but 2025 is going to be a year of change. Here’s how he gets work done at AppleInsider.
The AppleInsider weekend news hub and Zoom/podcasting studio.I only develop and write stories for AppleInsider on the weekends, hence my Weekend Editor title. As a result, I have a pretty modest setup and workflow compared to most of the full-timers.
Versatility for travel is one of my key requirements, since I am on the road at various times of the year. Even when I’m at home, I’m often in a cafe or occasionally doing local radio as a “computer guru,” or on Zoom teaching online tech classes.
Go Here to Read this Fast! How we work: Charles prepares for a big Apple tech refresh in 2025
Originally appeared here:
How we work: Charles prepares for a big Apple tech refresh in 2025