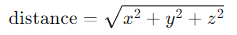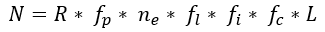The Real Odds of Encountering Alien Life (Part 5 of the Drake Equation Series)
Recap:
Throughout this series, we’ve explored the factors that could lead to the existence of alien civilizations, starting from the number of habitable planets to the probability that intelligent civilizations have developed communication technology. In this final article, we approach the ultimate question: Have we ever encountered alien life? And will we ever encounter it in the future?

Step 10: A Rational Approach to Extraterrestrial Encounters
The search for extraterrestrial life has long been a mix of science, speculation, and sensationalism. From UFO sightings to government UAP (Unidentified Aerial Phenomena) reports, the public imagination has been captivated by the idea of alien encounters. But, from a scientific standpoint, how likely is it that we’ve already encountered alien life — or ever will?
This is where a rational, data-driven approach comes into play. Using a combination of the Drake Equation, modern simulations, and Bayesian probability models, we can finally calculate the likelihood of past and future encounters.
Why This Step Matters
It’s easy to get caught up in the excitement of potential alien encounters, but the reality is far more nuanced. Even if intelligent civilizations exist in the galaxy, the chances of them overlapping with our civilization in time and proximity are incredibly small. This step will help quantify the likelihood of these encounters based on both past and future possibilities, giving us a clearer picture of the odds we’re facing.
Bayesian Probability and Alien Encounters
Bayesian reasoning allows us to update our probability estimates as new evidence (or lack thereof) emerges. In the case of alien encounters, we can use this approach to assess the probabilities of both past and future contact.
Let’s break down the Bayesian approach:
- P(H|E): The probability that aliens exist and we’ve encountered them given the current evidence.
- P(H): Our prior probability, or the initial assumption of how likely it is that alien encounters have occurred or will occur.
- P(E|H): The likelihood of the current evidence (e.g., no confirmed alien contact) assuming the hypothesis of an encounter is true.
- P(E): The overall probability of the evidence, which accounts for all possible hypotheses.
We’ll use this framework to calculate both past and future encounters.
Bayesian Monte Carlo Simulation for Alien Encounters: Understanding the Approach
To quantify the probabilities of past and future alien encounters, we employed a Bayesian framework combined with Monte Carlo simulations to manage the inherent uncertainty in the parameters. This section walks you through the rationale and methodology behind these two approaches before presenting the actual code.
Why Use Bayesian Analysis?
Bayesian analysis is a robust method for updating the probability of an event based on new evidence. In our case, the event in question is whether we have encountered, or will encounter, alien civilizations. By incorporating both prior knowledge and the available (though limited) evidence — like the absence of confirmed contact — we can refine our estimates and quantify the uncertainty around past and future alien encounters.
Bayes’ theorem allows us to calculate the posterior probabilities — in other words, the likelihood of alien encounters given our assumptions and observations. This process is essential because it continuously updates our understanding as new information emerges, whether it’s confirmed evidence of extraterrestrial life or further lack of contact.
Why Monte Carlo Simulations?
Given the uncertainty and variability in the parameters of the Drake Equation and other likelihoods related to alien encounters, it would be unrealistic to use a single set of fixed values to estimate the probabilities. Instead, Monte Carlo simulations let us sample a broad range of plausible values for each parameter, such as the likelihood of contact or the prior probability that alien life exists.
By running thousands of simulations with these different values, we can explore a range of outcomes rather than relying on rigid point estimates. The result is a more nuanced understanding of how likely past and future encounters are, along with a clearer picture of the probability distributions for each scenario.
Now, let’s dive into the actual code implementation:
**********************************;
**********************************;
/* Set the random seed for reproducibility */
data _null_;
call streaminit(1234);
run;
/* Number of simulations */
%let num_simulations = 100000;
/* Number of civilizations to generate */
%let num_civilizations = 2364;
/* Galactic radius and height in light years */
%let galactic_radius = 50000;
%let galactic_height = 1300;
/* Earth's position (assumed to be at 3/4 of the galactic radius) */
%let earth_position_x = &galactic_radius * 3 / 4;
%let earth_position_y = 0;
%let earth_position_z = 0;
/* Create a dataset to store civilization positions */
data civilization_positions;
length Civilization $10.;
input Civilization $ Position_X Position_Y Position_Z;
datalines;
Earth &earth_position_x &earth_position_y &earth_position_z
;
run;
/* Generate random positions for other civilizations */
data civilization_positions;
set civilization_positions;
do i = 1 to &num_civilizations;
Position_X = rand("Uniform") * &galactic_radius;
Position_Y = rand("Uniform") * 2 * &galactic_height - &galactic_height;
Position_Z = rand("Uniform") * 2 * &galactic_height - &galactic_height;
Civilization = "Civilization " || strip(put(i, 8.));
output;
end;
drop i;
run;
/* Calculate the distance between civilizations and Earth */
data civilization_distances;
set civilization_positions;
Distance = sqrt((Position_X - &earth_position_x)**2 + (Position_Y - &earth_position_y)**2 + (Position_Z - &earth_position_z)**2);
run;
/* Calculate the minimum distance to Earth for each civilization */
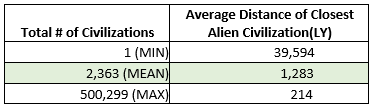
proc sql;
create table civilization_min_distance as
select Civilization, Distance as Min_Distance
from civilization_distances
order by Distance;
quit;
/* Calculate the probability of encountering civilizations based on distance */
data probability_encounter;
set civilization_min_distance;
Probability = 1 / (1 + Min_Distance);
run;
/* Calculate the average probability for each distance band */
proc sql;
create table average_probability as
select case
when Min_Distance <= 1000 then 'Close'
when Min_Distance > 1000 and Min_Distance <= 3000 then 'Medium'
when Min_Distance > 3000 then 'Far'
end as Distance_Band,
avg(Probability) as Average_Probability
from probability_encounter
group by case
when Min_Distance <= 1000 then 'Close'
when Min_Distance > 1000 and Min_Distance <= 3000 then 'Medium'
when Min_Distance > 3000 then 'Far'
end;
quit;
/* Print the result */
proc print data=average_probability;
run;
/* Select the closest civilization to Earth and its associated probability */
proc sql;
create table closest_civilization as
select Civilization, Min_Distance, Probability
from probability_encounter
where Min_Distance = (select min(Min_Distance) from probability_encounter);
quit;
/* Print the result */
proc print data=closest_civilization;
run;
/*Bayesian analysis for probability of encountering aliens in the past or future*/
/* Set seed for reproducibility */
%let num_iterations = 100;
/* Create Bayesian analysis dataset */
data bayesian_analysis;
call streaminit(123);
/* Define variables for posterior probabilities */
array posterior_past[&num_iterations];
array posterior_future[&num_iterations];
do i = 1 to &num_iterations;
/* Sample prior probabilities and likelihoods for past encounters */
prior_past = rand("Uniform", 0.0001, 0.01); /* P(Past encounter) */
likelihood_past_encounter = rand("Uniform", 0.001, 0.1); /* P(No contact | Past encounter) */
likelihood_no_encounter_past = rand("Uniform", 0.8, 0.99); /* P(No contact | No encounter) */
/* Calculate posterior probability for past encounter using Bayes' Theorem */
numerator_past = prior_past * likelihood_past_encounter;
denominator_past = numerator_past + (1 - prior_past) * likelihood_no_encounter_past;
posterior_past[i] = numerator_past / denominator_past;
/* Sample prior probabilities and likelihoods for future encounters */
prior_future = rand("Uniform", 0.001, 0.05); /* P(Future encounter) */
likelihood_future_encounter = rand("Uniform", 0.01, 0.1); /* P(No contact | Future encounter) */
likelihood_no_encounter_future = rand("Uniform", 0.8, 0.99); /* P(No contact | No encounter) */
/* Calculate posterior probability for future encounter using Bayes' Theorem */
numerator_future = prior_future * likelihood_future_encounter;
denominator_future = numerator_future + (1 - prior_future) * likelihood_no_encounter_future;
posterior_future[i] = numerator_future / denominator_future;
end;
/* Output the results */
do i = 1 to &num_iterations;
posterior_past_value = posterior_past[i];
posterior_future_value = posterior_future[i];
output;
end;
keep posterior_past_value posterior_future_value;
run;
/* Summary statistics for the posterior probabilities */
proc means data=bayesian_analysis mean std min max;
var posterior_past_value posterior_future_value;
run;
/* Distribution histograms for the posterior probabilities */
proc sgplot data=bayesian_analysis;
histogram posterior_past_value / transparency=0.5 fillattrs=(color=blue) binwidth=0.00001;
title "Distribution of Posterior Probabilities for Past Encounters";
run;
proc sgplot data=bayesian_analysis;
histogram posterior_future_value / transparency=0.5 fillattrs=(color=green) binwidth=0.0001;
title "Distribution of Posterior Probabilities for Future Encounters";
run;
With this code, we simulate both past and future alien encounters under a range of assumptions, enabling us to estimate the likelihood of each scenario using Bayesian reasoning. By the end of the process, we have distributions of probabilities for both past and future alien contact, which we’ll now analyze to gain further insights.
Analyzing the Table and Graphical Output
Table Output
The table presents the summary statistics for the posterior probabilities, which represent the likelihood of both past and future alien encounters:
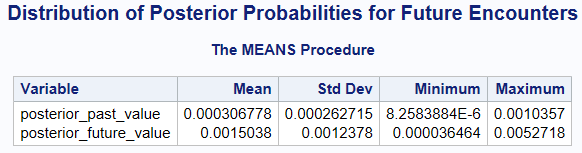
posterior_past_value:
- Mean: 0.000306778
- Std Dev: 0.000262715
- Minimum: 8.258388E-6
- Maximum: 0.0010357
posterior_future_value:
- Mean: 0.0015038
- Std Dev: 0.0012378
- Minimum: 0.000036464
- Maximum: 0.0052718
Interpretation:
- Past Encounters: The mean probability for past encounters is around 0.0003, or approximately 0.03%. In more intuitive terms, this translates to about a 1 in 3,260 chance that we’ve encountered aliens in the past.
- Future Encounters: The mean probability for future encounters is higher, at around 0.0015, or 0.15%. This translates to about a 1 in 667 chance of encountering aliens in the future.
The range of these values indicates that there is quite a bit of uncertainty, which makes sense given the limitations of the data and assumptions. The minimum value for past encounters is as low as 0.000008 (or 1 in 125,000), while the maximum value is closer to 0.001 (or 1 in 1,000). Future encounters range from 0.000036 (1 in 27,397) to 0.005 (or 1 in 190).
Graphical Output
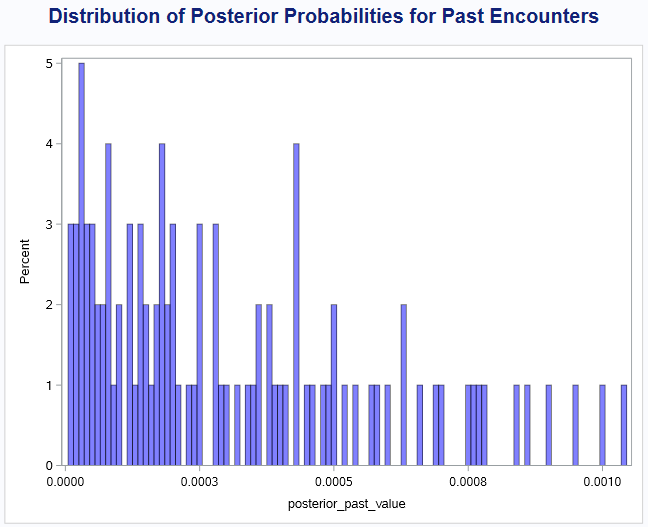
- Distribution of Posterior Probabilities for Past Encounters:
The histogram shows a wide distribution, with most probabilities clustering around the lower end, below 0.0005. This suggests that the likelihood of past encounters is generally low across our simulations, but there are still a few instances where the probability was higher, approaching 0.001 (or 1 in 1,000).
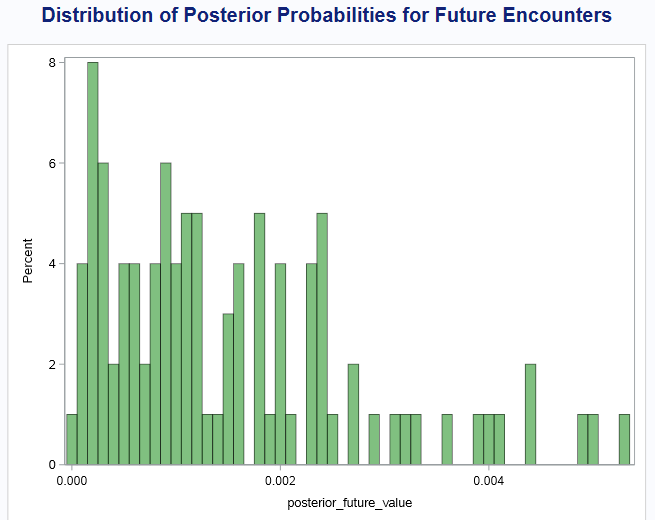
2. Distribution of Posterior Probabilities for Future Encounters:
The distribution for future encounters is more spread out, with the highest probability occurrences clustered between 0.0005 and 0.002. This indicates that future encounters, while still unlikely, have a higher probability than past encounters. The shape of the distribution suggests that while the odds of contact are low, there is a non-trivial chance that future encounters could happen, depending on how certain assumptions play out.
Key Takeaways and Probability Calculations
Past Encounters:
The mean posterior probability of a past encounter is approximately 0.0003. In terms of simple odds, this translates to a 1 in 3,260 chance that humanity has already encountered extraterrestrial life without realizing it. The wide distribution reflects uncertainty, with probabilities ranging from as low as 1 in 125,000 to as high as 1 in 1,000, depending on the assumptions we use for prior likelihoods and evidence.
Future Encounters:
The mean posterior probability for future encounters is 0.0015, which translates to a 1 in 667 chance that we will encounter alien life at some point in the future. While still unlikely, this higher probability compared to past encounters suggests a better (though still slim) chance of future contact. The distribution ranges from a 1 in 27,397 chance at the low end to a more optimistic 1 in 190 chance, reflecting the wide range of possible outcomes.
Tying It All Together: What Does This Mean?
The journey we’ve taken throughout this series has been a fascinating exploration of probability, uncertainty, and the grandest of questions: Are we alone in the universe? Using the Drake Equation as a framework, we’ve examined every step from the formation of habitable planets to the development of intelligent, communicative civilizations. But what does it all mean, and why did we take this approach?
The Bigger Picture
- Why We Did This: Our goal was simple, yet profound: to rationally assess the likelihood of alien civilizations existing and, even more importantly, whether we have — or will ever — encounter them. There is a lot of speculation in popular culture about UFOs, sightings, and mysterious signals, but we wanted to approach this scientifically. By working through the Drake Equation, using Monte Carlo simulations, and applying Bayesian reasoning, we attempted to put some tangible numbers to an otherwise nebulous question.
- How We Did It: The methodology we used isn’t about definitive answers but rather about understanding the range of possibilities. Each step of the Drake Equation brings with it huge uncertainties — how many habitable planets exist, how many develop life, and how many civilizations are sending signals into the cosmos. To handle this uncertainty, we turned to Monte Carlo simulations, which allowed us to account for a broad range of outcomes and calculate distributions instead of single estimates. Bayesian analysis then helped us refine these probabilities based on current evidence — or the lack thereof — providing more nuanced predictions about alien contact.
- What the Results Mean: The numbers might seem small at first glance, but they are significant in their implications. The odds of past contact (about 1 in 3,260) are low, which isn’t surprising given the lack of definitive evidence. Yet, these odds are not zero, and that in itself is worth noting — there is a chance, however small, that we have already encountered extraterrestrial life without realizing it.
- The probability of future contact is a bit more optimistic: around 1 in 667. While still a long shot, this suggests that if we continue searching, there is a small but tangible chance we could detect or communicate with alien civilizations at some point in the future. The future is uncertain, but with advancing technology and an ever-expanding field of study in astrobiology and space exploration, the possibility remains.
The Takeaway:
This analysis leaves us with a sobering but hopeful conclusion. The universe is vast, and the distances between stars — let alone civilizations — are staggering. The very structure of the cosmos, combined with the timescales involved in the rise and fall of civilizations, suggests that encounters are improbable but not impossible.
The true marvel here is not just in the numbers but in what they represent: the intersection of humanity’s curiosity and our capacity for rational, evidence-based exploration. We may be alone, or we may one day share a signal with another intelligent civilization. Either way, the work we’ve done to quantify the probabilities shows that the search itself is worthwhile. It reveals how much we still have to learn about the universe and our place in it.
While the odds may not be in our favor, the possibility of a future encounter — however remote — gives us reason to keep looking to the stars. The universe remains full of mysteries, and our journey to solve them continues. Whether or not we ever make contact, the search itself pushes the boundaries of science, philosophy, and our collective imagination.
This is where the work leaves us — not with concrete answers, but with profound questions that will continue to inspire curiosity, exploration, and wonder for generations to come. The search for extraterrestrial life is a search for understanding, not just of the cosmos, but of ourselves.
If you missed the previous parts, start here.
Unless otherwise noted, all images are by the author
Are We Alone? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Are We Alone?