Machine Learning Algorithms as a Mapping Between Spaces: From SVMs to Manifold Learning

Exploring the beauty of mapping between spaces in SVMs, autoencoders, and manifold learning (isomaps) algorithms

Introduction

In machine learning, understanding how algorithms process, interpret, and classify data relies heavily on the concept of “spaces.” In this context, a space is a mathematical construct where data points are positioned based on their features. Each dimension in the space represents a specific attribute or feature of the data, allowing algorithms to navigate a structured representation.

Feature Space and Input Space

The journey begins in the feature or input space, where each data point is a vector representing an instance in the dataset. To simplify, imagine an image where each pixel is a dimension in this space. The complexity and dimensionality of the space depend on the number and nature of the features. Working with high-dimensional spaces can be either enjoyable or frustrating for data practitioners.

Challenges in Low-dimensional Spaces

In low-dimensional spaces, not all relationships or patterns in the data are easily identifiable. Linear separability, which is the ability to divide classes with a simple linear boundary, is often unachievable. This limitation becomes more apparent in complex datasets where the interaction of features creates non-linear patterns that cannot be captured by simple linear models.

In this article, we will explore machine learning algorithms in the perspective of mapping and interaction between different spaces. We will start with support vector machines (SVMs) as an example of simplicity, then move on to autoencoders, and finally, we will discuss manifold learning and Isomaps.

Please note that the code examples in this article are for demonstration and may not be optimized. I encourage you to modify, improve and try the code with different datasets to deepen your understanding and gain further insights.

Support Vector Machines

Support Vector Machines (SVMs) are known machine learning algorithms that excel at classifying data. As we mentioned at the beginning:

In lower dimensions, linear separability is often impossible, which means it’s difficult to divide classes with a simple linear boundary.

SVMs overcomes this difficulty by transforming data into a higher-dimensional space, making it easier to separate and classify. To illustrate this, let’s look at an example. The code below generates synthetic data that is clearly not linearly separable in its original space.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles

# Generate synthetic data that is not linearly separable
X, y = make_circles(n_samples=100, factor=0.5, noise=0.05)

# Visualize the data
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Original 2D Data')
plt.show()

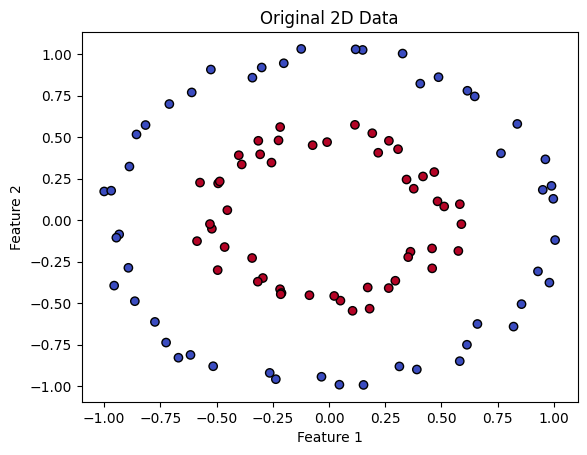
SVMs use a mapping between spaces to separate different classes. They lift the data from a lower dimensional space to a higher dimensional one. In this new space, SVMs find the optimal hyperplane, which is a decision boundary that separates the classes. It’s like finding the perfect line that divides groups in a two-dimensional graph, but in a more complex, multidimensional universe.

In the provided data, one class is close to the origin and another class is far from the origin. Let’s look at a typical example to understand how this data becomes separable when transformed into higher dimensions.

We will transform each 2D point (x, y) to a 3D point (x, y, z), where z = x² + y². The transformation adds a new third dimension based on the squared distance from the origin in the 2D space. Points that are farther from the origin in the 2D space will be higher in the 3D space because their squared distance is larger.

from mpl_toolkits.mplot3d import Axes3D

# Transform the 2D data to 3D for visualization
Z = X[:, 0]**2 + X[:, 1]**2  # Use squared distance from the origin as the third dimension

# Visualize the 3D data
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], Z, c=y, cmap=plt.cm.coolwarm)

# Set labels
ax.set_xlabel('Feature 1')
ax.set_ylabel('Feature 2')
ax.set_zlabel('Transformed Feature')

# Set the viewpoint
elevation_angle = 15  # Adjust this to change the up/down angle
azimuth_angle = 45  # Adjust this to rotate the plot
ax.view_init(elev=elevation_angle, azim=azimuth_angle)

plt.show()

You can notice from the output above that after this transformation, our data becomes linearly separable by a 2D hyperplane.

Another example is the effectiveness of drug dosages. A patient is only cured if the dosage falls within a certain range. Dosages that are too low or too high are ineffective. This scenario naturally creates a dataset that is not linearly separable, making it a good candidate for demonstrating how a polynomial kernel can help.

# Train the SVM model on the 2D data
svc = SVC(kernel='linear', C=1.0)
svc.fit(X, y)

# Create a function to plot decision boundary
def plot_svc_decision_function(model, plot_support=True):
    """Plot the decision function for a 2D SVC"""
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # create grid to evaluate model
    xx = np.linspace(xlim[0], xlim[1], 30)
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = model.decision_function(xy).reshape(XX.shape)

    # plot decision boundary and margins
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])
    # plot support vectors
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1],
                   s=300, linewidth=1, facecolors='none', edgecolors='k')

# Adjust the figure size for better visualization
plt.figure(figsize=(8, 5))

# Scatter plot for original dosage points
plt.scatter(dosages, np.zeros_like(dosages), c=y, cmap='bwr', marker='s', s=50, label='Original Dosages')

# Scatter plot for dosage squared points
plt.scatter(dosages, squared_dosages, c=y, cmap='bwr', marker='^', s=50, label='Squared Dosages')

# Calling the function to plot the SVM decision boundary
plot_svc_decision_function(svc)

# Expanding the limits to ensure all points are visible
plt.xlim(min(dosages) - 1, max(dosages) + 1)
plt.ylim(min(squared_dosages) - 10, max(squared_dosages) + 10)

# Adding labels, title and legend
plt.xlabel('Dosage')
plt.ylabel('Dosage Squared')
plt.title('SVM Decision Boundary with Original and Squared Dosages')
plt.legend()

# Display the plot
plt.show()

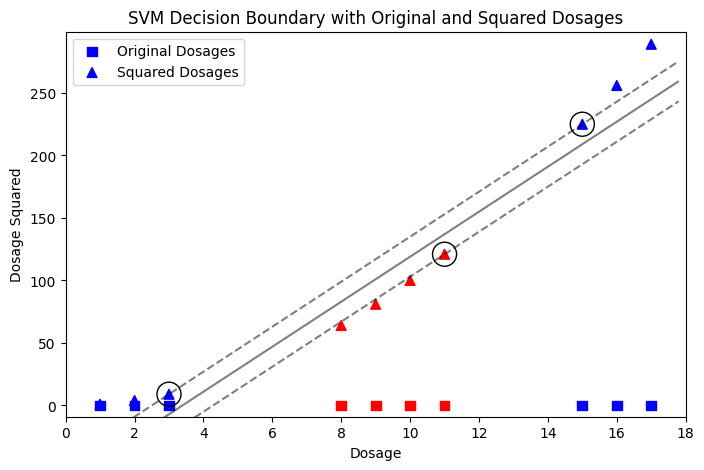
In the two examples above, we take advantage of our knowledge about the data. For instance, in first example we know that we have two classes: one close to the origin and another far from the origin. This is what the algorithm does through training and fine-tuning — it finds a suitable space where the data can be linearly separated.

The great thing here is that SVMs don’t map data into higher dimensions as this would be very complex computationally. Instead, they compute the relationship between the data as if it were in higher dimensions using the dot product. This is called the “Kernel trick.” I will explain SVM kernels in another article.

Autoencoders

Autoencoders are truly amazing and beautiful architectures that capture my imagination. They have a wide range of applications across various domains, utilizing diverse types of autoencoders.

They basically consist of an encoder and a decoder, the encoder takes your input and encode/compress it, a process in which we move from a high-dimensional space to a more compact, lower-dimensional one. What’s truly interesting is how the decoder then takes this condensed representation and reconstructs the original data in the higher-dimensional space. The natural question is: how is it possible to go back to the original space from a significantly reduced dimension?

Let’s consider an HD image with a resolution of 720×720 pixels. Storing and transmitting this image requires a lot of memory and bandwidth. Autoencoders solve this problem by compressing the image into a lower-dimensional space, like a 32×32 representation called the ‘bottleneck’. The encoder’s job is done at this point. The decoder takes over, trying to rebuild the original image from this compressed form.

This process is similar to sharing images on platforms like WhatsApp. The image is encoded to a lower quality for transmission and then decoded on the receiver’s end. The difference in quality between the original and received image is called ‘reconstruction error’, which is common in autoencoders.

In autoencoders, we can think of it as an interaction between 3 spaces:

1. The input space.
2. The latent representation space (the bottleneck).
3. The output space.

The beauty here is that we can see the autoencoder as something that operates in these 3 spaces. It takes advantage of the latent spaces to remove any noisy or unnecessary information from the input space, resulting in a very compact representation with core information about the input space. It does this by trying to mirror the input space in the output space, reducing the difference between the two spaces or the reconstruction error.

Convolutional Autoencoders: Encoding Complexity into Simplicity

The code below shows an example of a convolutional autoencoder, which is a type of autoencoders that works well with images. We will use the popular MNIST dataset[LeCun, Y., Cortes, C., & Burges, C.J. (1998). The MNIST Database of Handwritten Digits. Retrieved from TensorFlow, CC BY 4.0], which contains 28×28 pixel grayscale images of handwritten digits. The encoder plays a crucial role by reducing the dimensionality of the data from 784 elements to a smaller, more condensed form. The decoder then aims to reconstruct the original high-dimensional data from this lower-dimensional representation. However, this reconstruction is not perfect and some information is lost. The autoencoder overcomes this challenge by learning to prioritize the most important features of the data.

import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt

# Load MNIST dataset
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), 28, 28, 1))
x_test = x_test.reshape((len(x_test), 28, 28, 1))

# Define the convolutional autoencoder architecture
input_img = layers.Input(shape=(28, 28, 1))

# Encoder
x = layers.Conv2D(16, (3, 3), activation='relu', padding='same')(input_img)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
encoded = layers.MaxPooling2D((2, 2), padding='same')(x)

# Decoder
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(16, (3, 3), activation='relu', padding='same')(x)
x = layers.UpSampling2D((2, 2))(x)
decoded = layers.Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)

# Autoencoder model
autoencoder = tf.keras.Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder.fit(x_train, x_train, epochs=10, batch_size=64, validation_data=(x_test, x_test))

# Visualization
# Sample images
sample_images = x_test[:8]
# Reconstruct images
reconstructed_images = autoencoder.predict(sample_images)

# Plot original images and reconstructed images
fig, axes = plt.subplots(nrows=2, ncols=8, figsize=(14, 4))
for i in range(8):
    axes[0, i].imshow(sample_images[i].squeeze(), cmap='gray')
    axes[0, i].set_title("Original")
    axes[0, i].axis('off')
    axes[1, i].imshow(reconstructed_images[i].squeeze(), cmap='gray')
    axes[1, i].set_title("Reconstructed")
    axes[1, i].axis('off')
plt.show()

The output above shows how well the autoencoder works. It displays pairs of images: the original digit images and their reconstructions after encoding and decoding. This example proves that the encoder captures the essence of the data in a smaller form and the decoder can approximate the original image, even though some information is lost during compression.

Now, let’s go further and visualize the learned latent space (the bottleneck). We will use PCA and t-SNE, two techniques to reduce dimensions, to show the compressed data points on a 2D plane. This step is important because it helps us see how the autoencoder organizes the data in the latent space and shows any natural clusters of similar digits. We used PCA and t-SNE together just to compare how well they work.

# Encode all the test data
encoded_imgs = encoder.predict(x_test)

# Reduce dimensionality using PCA
pca = PCA(n_components=2)
pca_result = pca.fit_transform(encoded_imgs)

# Reduce dimensionality using t-SNE
tsne = TSNE(n_components=2, perplexity=30, n_iter=300)
tsne_result = tsne.fit_transform(encoded_imgs)



# Visualization using PCA
plt.figure(figsize=(20, 10))
plt.subplot(1, 2, 1)
plt.scatter(pca_result[:, 0], pca_result[:, 1], c=y_test, cmap=plt.cm.get_cmap("jet", 10))
plt.colorbar(ticks=range(10))
plt.title('PCA Visualization of Latent Space')

# Visualization using t-SNE
plt.subplot(1, 2, 2)
plt.scatter(tsne_result[:, 0], tsne_result[:, 1], c=y_test, cmap=plt.cm.get_cmap("jet", 10))
plt.colorbar(ticks=range(10))
plt.title('t-SNE Visualization of Latent Space')

plt.show()

Comparing the two resulted graphs, t-SNE is better than PCA at separating different classes of digits in the latent space visualization(it captures non-linearity). It creates distinct clusters with minimal overlap between classes. The autoencoder compresses images into a lower dimensional space but still captures enough information to distinguish between different digits, as shown in the t-SNE graph.

An important note here is that t-SNE is a non-linear technique used for visualizing high-dimensional data. It preserves local data structures, making it useful for identifying clusters and patterns visually. However, it is not typically used for feature reduction in machine learning.

But what does this autoencoder probably learn?

Generally speaking, one can say that an autoencoder like this learns the basic and simple edges and textures, moving to parts of the digits like loops and lines and how they are arranged, and finally understanding whole digits(hierarchical characteristics), all this while capturing the unique essence of each digit in a compact form. It can guess missing parts of an image and recognizes common patterns in how digits are written.

Manifold learning: The Blessing of Non-Uniformity

In a previous article titled Curse of Dimensionality: An Intuitive Exploration, I explored the concept of the “Curse of dimensionality”, which refers to the problems and challenges that arises when working with data in higher dimensions, making the job of ML algorithms harder in many ways.

Here come the manifold learning algorithms, driven by the blessing of non-uniformity, the uneven distribution or variation of data points within a given space or dataset.

The fundamental assumption underlying manifold learning is that high-dimensional data actually lies on or near a lower-dimensional manifold within the high-dimensional space. This concept is based on the idea that although the data might exist in a high-dimensional space due to the way it’s measured or recorded, the intrinsic dimensions that effectively describe the data and its structure are much lower.

Let’s generate the famous Swiss roll dataset and use it as an example of non-uniformity in higher-dimensional spaces. In its original form, this dataset looks like a chaotic mess of data points. But beneath this chaos, there is hidden order — a low-dimensional structure that includes the important features of the data. Manifold learning techniques, like Isomaps, take advantage of this non-uniformity. By mapping data points from the high-dimensional space to a lower-dimensional one, Isomap shows us the intrinsic shape of the Swiss roll. It keeps the richness of the original data while revealing the underlying structure — a 2D projection that captures the non-uniformity of the high-dimensional space:

import numpy as np
import matplotlib.pyplot as plt
from sklearn import manifold, datasets

# Generate a Swiss Roll dataset
X, color = datasets.make_swiss_roll(n_samples=1500)

# Apply Isomap for dimensionality reduction
iso = manifold.Isomap(n_neighbors=10, n_components=2)
X_iso = iso.fit_transform(X)

# Plot the 3D Swiss Roll
fig = plt.figure(figsize=(15, 8))

# Create a 3D subplot
ax = fig.add_subplot(121, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)

# Set the viewing angle
elevation_angle = 30  # adjust this for elevation
azimuthal_angle = 45  # adjust this for azimuthal angle
ax.view_init(elev=elevation_angle, azim=azimuthal_angle)

ax.set_title("Original Swiss Roll")

# Plot the 2D projection after Isomap
ax = fig.add_subplot(122)
ax.scatter(X_iso[:, 0], X_iso[:, 1], c=color, cmap=plt.cm.Spectral)
plt.axis('tight')
ax.set_title("2D projection by Isomap")

# Show the plots
plt.show()

Let’s look at the output above:

We have two colorful illustrations. On the left, there’s a 3D Swiss roll with a rainbow of colors that spiral together. It shows how each shade transitions into the next, marking a path through the roll.

Now, on the right. There’s a 2D spread of the same colors. Even though the shape has changed the order and flow of colors still tell the same story of the original data. The order and connections between points are preserved, as if the Swiss roll was carefully unrolled onto a flat surface so we can see the entire pattern at once.

Conclusion

This article started by exploring the concept of spaces, which are the mathematical constructs where data points are positioned based on their features/attributes. We examined how Support Vector Machines (SVMs) leverage the idea of mapping data into higher-dimensional spaces to address the challenge of non-linear separability in lower spaces.

Then we moved on to autoencoders, an elegant and truly beautiful architecture that maps between 3 spaces, the input space, that gets compressed to a much lower latent representation(the bottleneck), and then comes the decoder to take the lead aiming to reconstruct the original input from this lower representation while minimizing the reconstruction error.

We also explored manifold learning, and the blessing that we get from non-uniformity as a way to overcome the curse of dimensionality by simplifying complex datasets without losing important details.

If you made it this far, I would like to thank you for your time reading this, I hope you found it enjoyable and useful, please feel free to point out any mistakes or misconceptions in my article, your feedback and suggestions are also greatly appreciated.

Machine Learning Algorithms as a Mapping Between Spaces: From SVMs to Manifold Learning was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.