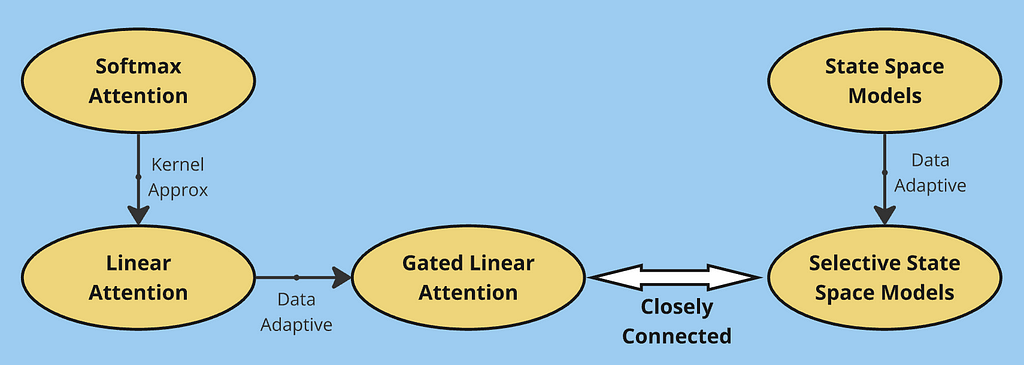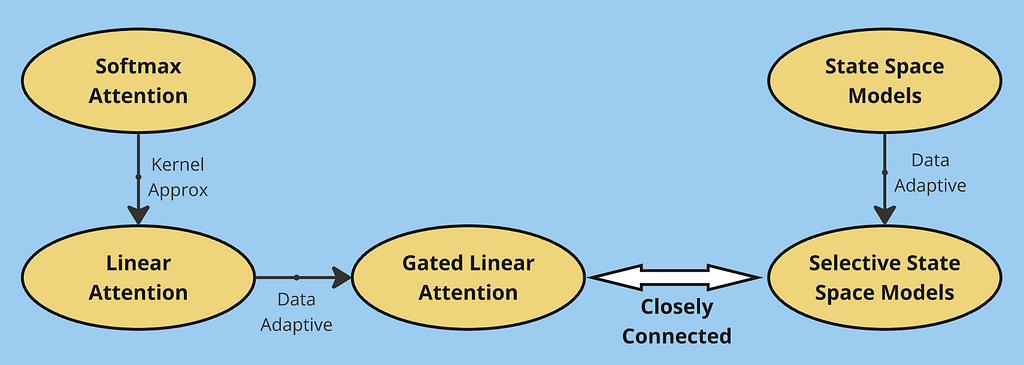
Breaking the quadratic barrier: modern alternatives to softmax attention
Large Languange Models are great but they have a slight drawback that they use softmax attention which can be computationally intensive. In this article we will explore if there is a way we can replace the softmax somehow to achieve linear time complexity.

Attention Basics
I am gonna assume you already know about stuff like ChatGPT, Claude, and how transformers work in these models. Well attention is the backbone of such models. If we think of normal RNNs, we encode all past states in some hidden state and then use that hidden state along with new query to get our output. A clear drawback here is that well you can’t store everything in just a small hidden state. This is where attention helps, imagine for each new query you could find the most relevant past data and use that to make your prediction. That is essentially what attention does.
Attention mechanism in transformers (the architecture behind most current language models) involve key, query and values embeddings. The attention mechanism in transformers works by matching queries against keys to retrieve relevant values. For each query(Q), the model computes similarity scores with all available keys(K), then uses these scores to create a weighted combination of the corresponding values(Y). This attention calculation can be expressed as:

This mechanism enables the model to selectively retrieve and utilize information from its entire context when making predictions. We use softmax here since it effectively converts raw similarity scores into normalized probabilities, acting similar to a k-nearest neighbor mechanism where higher attention weights are assigned to more relevant keys.
Okay now let’s see the computational cost of 1 attention layer,
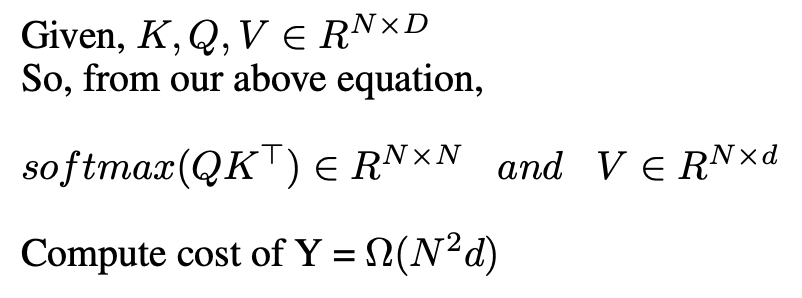
Softmax Drawback
From above, we can see that we need to compute softmax for an NxN matrix, and thus, our computation cost becomes quadratic in sequence length. This is fine for shorter sequences, but it becomes extremely computationally inefficient for long sequences, N=100k+.
This gives us our motivation: can we reduce this computational cost? This is where linear attention comes in.
Linear Attention
Introduced by Katharopoulos et al., linear attention uses a clever trick where we write the softmax exponential as a kernel function, expressed as dot products of feature maps φ(x). Using the associative property of matrix multiplication, we can then rewrite the attention computation to be linear. The image below illustrates this transformation:

Katharopoulos et al. used elu(x) + 1 as φ(x), but any kernel feature map that can effectively approximate the exponential similarity can be used. The computational cost of above can be written as,

This eliminates the need to compute the full N×N attention matrix and reduces complexity to O(Nd²). Where d is the embedding dimension and this in effect is linear complexity when N >>> d, which is usually the case with Large Language Models
Okay let’s look at the recurrent view of linear attention,

Okay why can we do this in linear attention and not in softmax? Well softmax is not seperable so we can’t really write it as product of seperate terms. A nice thing to note here is that during decoding, we only need to keep track of S_(n-1), giving us O(d²) complexity per token generation since S is a d × d matrix.
However, this efficiency comes with an important drawback. Since S_(n-1) can only store d² information (being a d × d matrix), we face a fundamental limitation. For instance, if your original context length requires storing 20d² worth of information, you’ll essentially lose 19d² worth of information in the compression. This illustrates the core memory-efficiency tradeoff in linear attention: we gain computational efficiency by maintaining only a fixed-size state matrix, but this same fixed size limits how much context information we can preserve and this gives us the motivation for gating.
Gated Linear Attention
Okay, so we’ve established that we’ll inevitably forget information when optimizing for efficiency with a fixed-size state matrix. This raises an important question: can we be smart about what we remember? This is where gating comes in — researchers use it as a mechanism to selectively retain important information, trying to minimize the impact of memory loss by being strategic about what information to keep in our limited state. Gating isn’t a new concept and has been widely used in architectures like LSTM
The basic change here is in the way we formulate Sn,
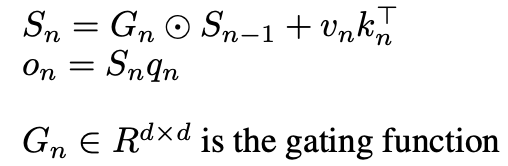
There are many choices for G all which lead to different models,

A key advantage of this architecture is that the gating function depends only on the current token x and learnable parameters, rather than on the entire sequence history. Since each token’s gating computation is independent, this allows for efficient parallel processing during training — all gating computations across the sequence can be performed simultaneously.
State Space Models
When we think about processing sequences like text or time series, our minds usually jump to attention mechanisms or RNNs. But what if we took a completely different approach? Instead of treating sequences as, well, sequences, what if we processed them more like how CNNs handle images using convolutions?
State Space Models (SSMs) formalize this approach through a discrete linear time-invariant system:
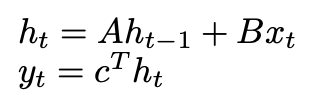
Okay now let’s see how this relates to convolution,
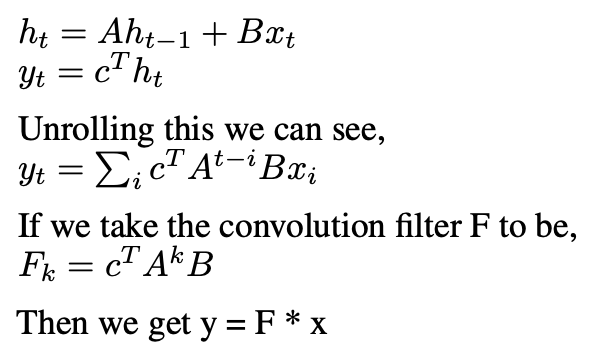
where F is our learned filter derived from parameters (A, B, c), and * denotes convolution.
H3 implements this state space formulation through a novel structured architecture consisting of two complementary SSM layers.

Here we take the input and break it into 3 channels to imitate K, Q and V. We then use 2 SSM and 2 gating to kind of imitate linear attention and it turns out that this kind of architecture works pretty well in practice.
Selective State Space Models
Earlier, we saw how gated linear attention improved upon standard linear attention by making the information retention process data-dependent. A similar limitation exists in State Space Models — the parameters A, B, and c that govern state transitions and outputs are fixed and data-independent. This means every input is processed through the same static system, regardless of its importance or context.
we can extend SSMs by making them data-dependent through time-varying dynamical systems:
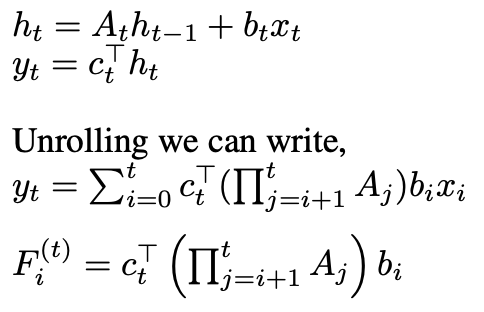
The key question becomes how to parametrize c_t, b_t, and A_t to be functions of the input. Different parameterizations can lead to architectures that approximate either linear or gated attention mechanisms.
Mamba implements this time-varying state space formulation through selective SSM blocks.

Mamba here uses Selective SSM instead of SSM and uses output gating and additional convolution to improve performance. This is a very high-level idea explaining how Mamba combines these components into an efficient architecture for sequence modeling.
Conclusion
In this article, we explored the evolution of efficient sequence modeling architectures. Starting with traditional softmax attention, we identified its quadratic complexity limitation, which led to the development of linear attention. By rewriting attention using kernel functions, linear attention achieved O(Nd²) complexity but faced memory limitations due to its fixed-size state matrix.
This limitation motivated gated linear attention, which introduced selective information retention through gating mechanisms. We then explored an alternative perspective through State Space Models, showing how they process sequences using convolution-like operations. The progression from basic SSMs to time-varying systems and finally to selective SSMs parallels our journey from linear to gated attention — in both cases, making the models more adaptive to input data proved crucial for performance.
Through these developments, we see a common theme: the fundamental trade-off between computational efficiency and memory capacity. Softmax attention excels at in-context learning by maintaining full attention over the entire sequence, but at the cost of quadratic complexity. Linear variants (including SSMs) achieve efficient computation through fixed-size state representations, but this same optimization limits their ability to maintain detailed memory of past context. This trade-off continues to be a central challenge in sequence modeling, driving the search for architectures that can better balance these competing demands.
To read more on this topics, i would suggest the following papers:
Acknowledgement
This blog post was inspired by coursework from my graduate studies during Fall 2024 at University of Michigan. While the courses provided the foundational knowledge and motivation to explore these topics, any errors or misinterpretations in this article are entirely my own. This represents my personal understanding and exploration of the material.
Linearizing Attention was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Linearizing Attention