ITT vs LATE: Estimating Causal Effects with IV in Experiments with Imperfect Compliance

Intuition, step-by-step script, and assumptions needed for the use of IV

In many experiments, not all individuals assigned to receive a treatment actually take it or use it. For example, a company may send discount coupons to customers, intending for them to use these coupons to make a purchase now, which could subsequently increase their future purchases. However, not all customers will redeem the coupon.

This scenario represents “imperfect compliance” (see here), where treatment assignment does not always lead to treatment uptake. To estimate the impact of offering the coupon on future customer purchases, we must distinguish between two main approaches:

• Intention to treat effect (ITT): Estimates the effect of being assigned to receive the coupon, regardless of whether it was used.
• Local average treatment effect (LATE): Estimates the effect of treatment among those who complied with the assignment — those who used the coupon because they were assigned to receive it.

This tutorial introduces the intuition behind these methods, their assumptions, and how to implement them using R (see script here). We will also discuss two-stage least squares (2SLS), the method used to estimate LATE.

Intuition

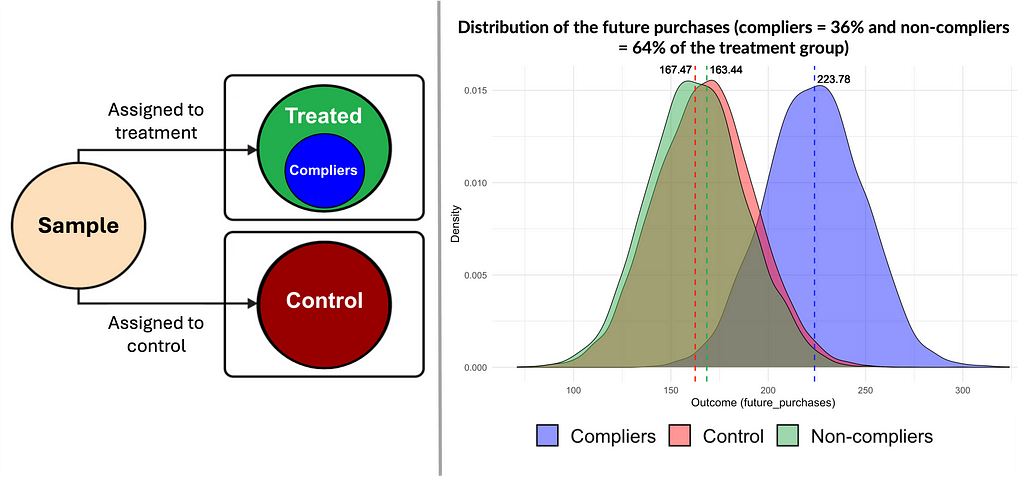
In experiments with imperfect compliance, treatment assignment (e.g., receiving a coupon) does not perfectly correspond to consuming the treatment (e.g., using the coupon). So simply comparing the treatment group to the control group may lead to misleading conclusions, as the effect of the treatment among those who took it (the blue group in the figure below) gets diluted within the larger treatment group (the green group).

To deal with this situation, we use two main approaches:

Intention-to-treat (ITT)

It measures the effect of being assigned to a treatment, regardless of whether individuals actually follow through with it. In our example, it compares the future average purchases of customers assigned to receive a coupon (treatment group) with those who were not (control group). This method is useful for understanding the effect of the assignment itself, but it may underestimate the treatment’s impact, as it includes individuals who did not use the coupon.

Local average treatment effect (LATE)

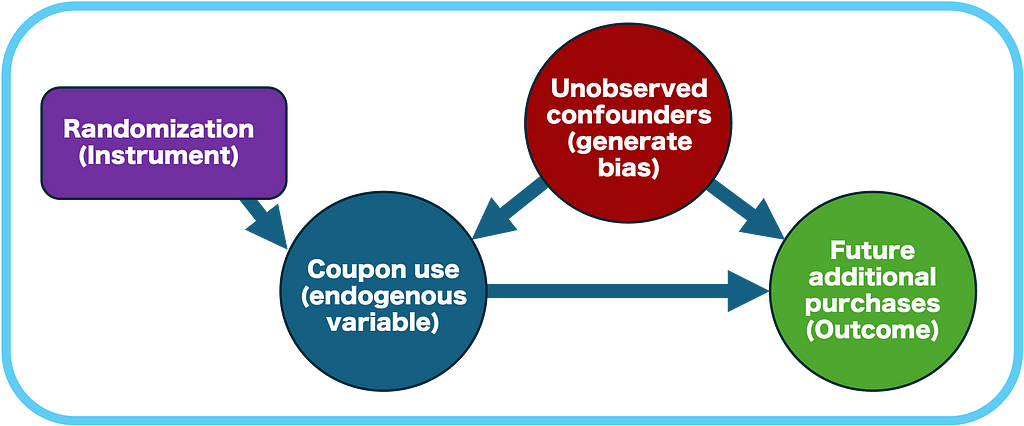
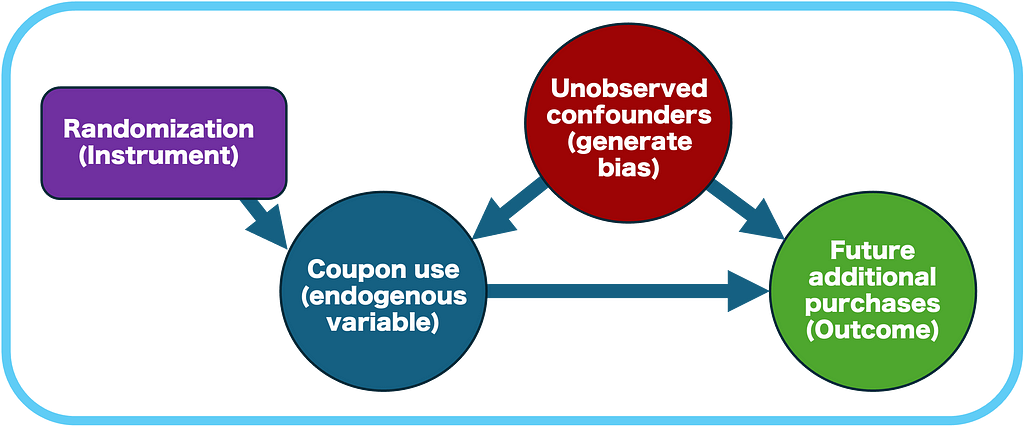
Here we use the instrumental variables (IV) method to estimate the local average treatment effect, which is the causal effect of treatment among those who complied with the assignment (“compliers”) — i.e., those who used the coupon because they were assigned to receive it. In summary:

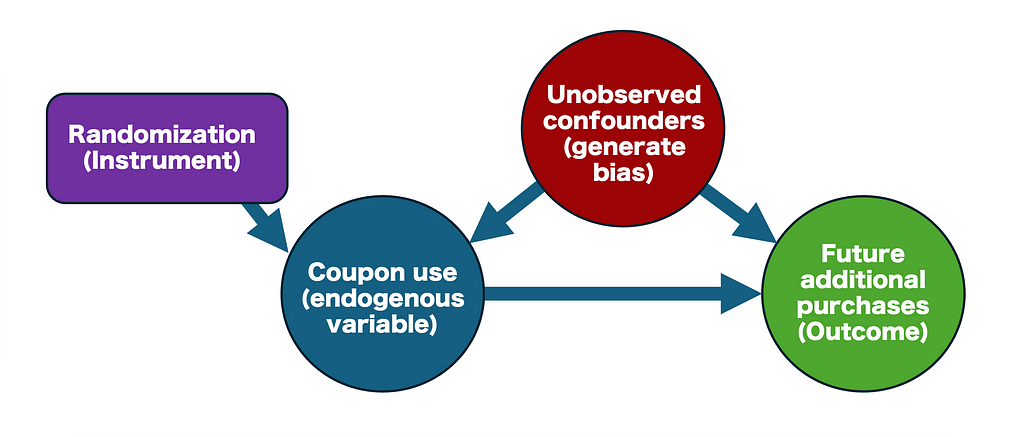
• The random assignment to treatment (receiving a coupon) is used as an instrumental variable that strongly predicts actual treatment uptake (using the coupon).
• The IV must meet specific assumptions (relevance, exogeneity, and exclusion restriction) that we will discuss in detail.
• The IV isolates the part of variation in coupon use that’s attributable to random assignment, eliminating the influence of unobserved factors that could bias the estimate (see more on “selection bias” here).
• The LATE estimates the effect of treatment by adjusting the impact of treatment assignment (ITT) for the compliance rate (the probability of using the coupon given that the customer was assigned).
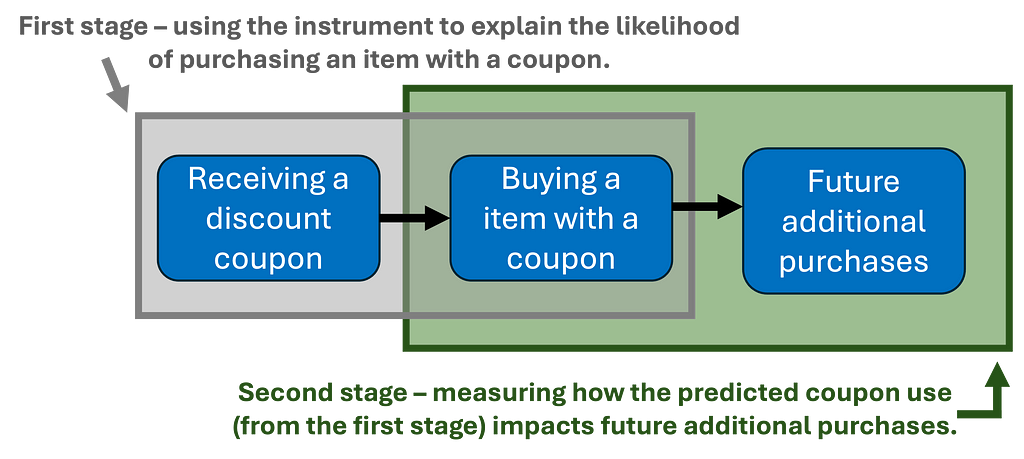
• It is estimated via two-stage least squares (2SLS), in which each stage is illustrated in the figure below. An intuitive explanation of this method is discussed in section 5 here.

Assumptions and limitations

While the ITT estimate can be obtained directly by using OLS , IV methods require strong assumptions to provide valid causal estimates. Fortunately, those assumptions tend to be met in the experimental scenario:

Instrument relevance

The instrumental variable (in this case, assignment to the treatment group) must be correlated with the endogenous variable whose effect on future purchases we want to measure (coupon usage). In other words, random assignment to receive a coupon should significantly increase the likelihood that a customer uses it. This is tested via the magnitude and statistical significance of the treatment assignment coefficient in the first stage regression.

Instrument exogeneity and exclusion restriction

The instrumental variable must be independent of any unobserved factors that influence the outcome (future purchases). It should impact the outcome only through its effect on the endogenous variable (coupon usage).

In simpler terms, the instrument should influence the outcome only by affecting coupon usage, and not through any other pathway.

In our scenario, the random assignment of coupons ensures that it is not correlated with any unobserved customer characteristics that could affect future purchases. Randomization also implies that the impact of being assigned a coupon will primarily depend on whether the customer chooses to use it or not.

Limitations and challenges

1. The LATE provides the causal effect only for “compliers” — customers who used the coupon because they received it, and this effect is specific to this group (local validity only). It cannot be generalized to all customers or those who used the coupon for other reasons.
2. When compliance rates are low (meaning only a small proportion of customers respond to the treatment), the estimated effect becomes less precise, and the findings are less reliable. Since the effect is based on a small number of compliers, it is also difficult to determine if the results are meaningful for the broader population.
3. The assumptions of exogeneity and exclusion restriction are not directly testable, meaning that we must rely on the experimental design or on theoretical arguments to support the validity of the IV implementation.

Hands-on with instrumental variables using R

Now that we understand the intuition and assumptions, we will apply these techniques in an example to estimate both ITT and LATE in R. We will explore the following scenario, reproduced in this R script:

An e-commerce company wants to assess whether the use of discount coupons increases future customer purchases. To circumvent selection bias, coupons were randomly sent to a group of customers, but not all recipients used them. Additionally, customers who did not receive a coupon had no access to it.

I simulated a dataset representing that situation:

• treatment: Half of the customers were randomly assigned to receive the coupon (treatment = 1) while the other half did not receive (treatment = 0).
• coupon_use: Among the individuals who received treatment, those who used the coupon to make a purchase are identified by coupon_use = 1.
• income and age: simulated covariates that follow a normal distribution.
• prob_coupon_use: To make this more realistic, the probability of coupon usage varies among those who received the coupons. Individuals with higher income and lower age tend to have a higher likelihood of using the coupons.
• future_purchases: The outcome, future purchases in R$, is also influenced by income and age.
• past_purchases: Purchases in R$ from previous months, before the coupon assignment. This should not be correlated with receiving or using a coupon after we control for the covariates.
• Finally, the simulated effect of coupon usage for customers who used the coupon is set to “true_effect <- 50“. This means that, on average, using the coupon increases future purchases by R$50 for those who redeemed it.

Verifying Assumptions

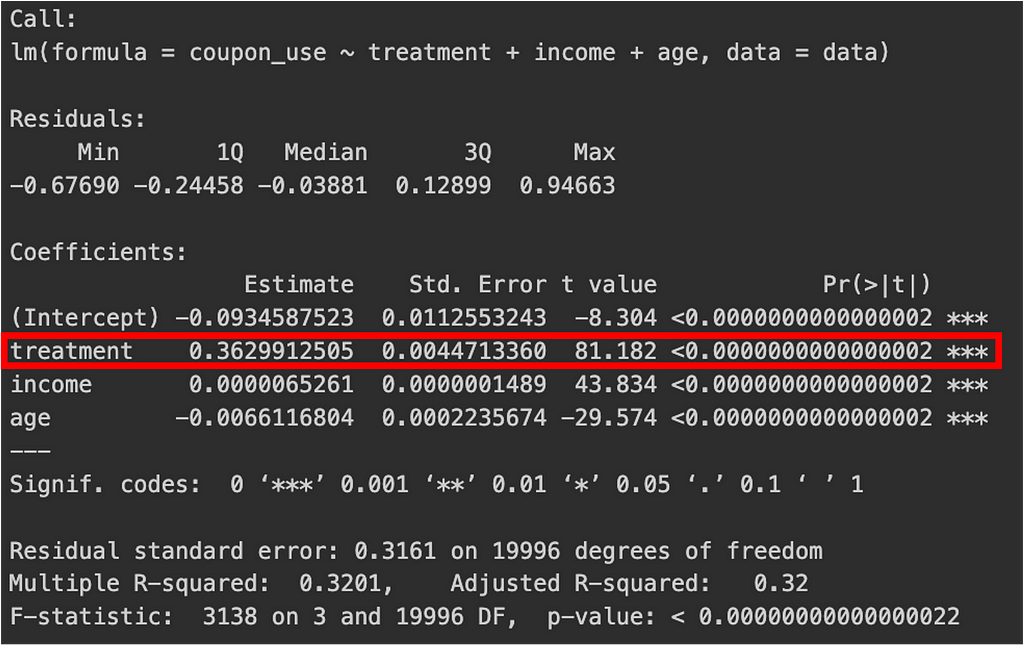
Instrument relevance: The first stage regression explains the relationship between belonging to the treatment group and the usage of the coupon. In this regression, the coefficient for “treatment” was 0.362, meaning that ~36% of the treatment group used the coupon. The p-value for this coefficient was < 0.01, with a t-statistic of 81.2 (substantial), indicating that treatment assignment (receiving a coupon) significantly influences coupon use.

Instrument exogeneity and exclusion restriction: By construction, since assignment is random, the instrument is not correlated with unobserved factors that affect future purchases. But in any case, these assumptions are indirectly testable via the two sets of results below:

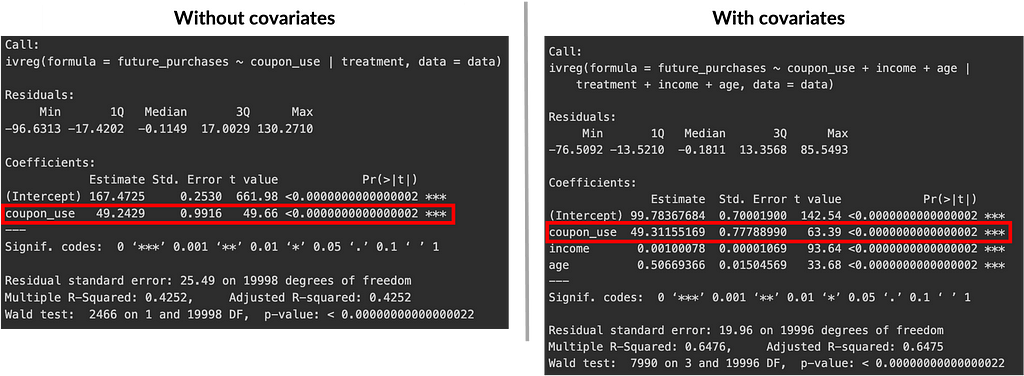
The first set includes regression results from the first (only in the script) and second stages (below), with and without covariates. These should yield similar results to support the idea that our instrument (coupon assignment) affects the outcome (future purchases) only through the endogenous variable (coupon use). Without covariates, the estimated effect was 49.24 with a p-value < 0.01, and with covariates, it was 49.31 with a p-value < 0.01.

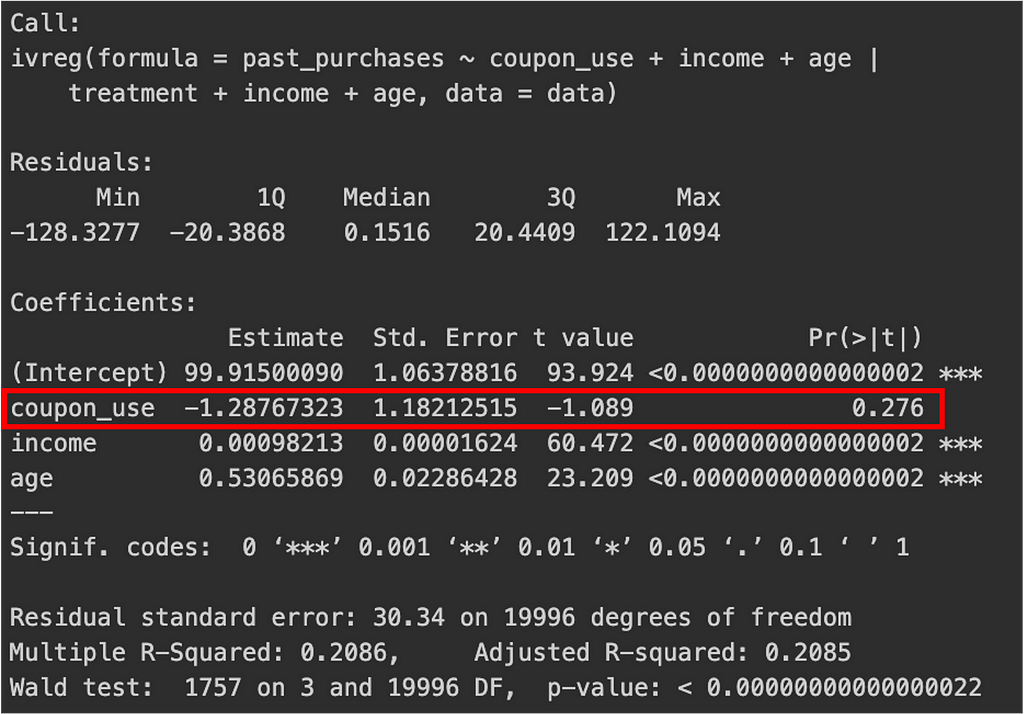
The second set involved a placebo test to determine whether the instrument affects past purchases (which it logically shouldn’t). This test suggests that the instrument does not have a direct effect on the outcome outside of its effect through the endogenous variable. The estimated effect, with or without covariates, was close to zero and not statistically significant.

LATE with two-stage least squares (2SLS)

Due to the nature of the indirect tests discussed above, we ended up anticipating the results of our main analysis, including the LATE (see the second figure of the subsection “Verifying Assumptions”). But now let’s go into more detail about this estimation process, which involves two steps using the 2SLS method:

1. First stage: We regress coupon usage on treatment assignment. This generates predicted values of coupon usage, isolating the portion attributable to random assignment.
2. Second stage: We take the predicted coupon usage from the first stage and regress it against future purchases. This step allows us to estimate the causal impact of coupon usage.

first_stage <- lm(coupon_use ~ treatment + income + age, data = data)
second_stage <- ivreg(future_purchases ~ coupon_use + income + age | treatment + income + age, data = data)

By applying the 2SLS method, we derive an unbiased estimate of the causal effect of coupon usage specifically for those who comply with the treatment, effectively filtering out the influence of random assignment.

Estimating causal effects

ITT estimate: It measures the average effect that offering a coupon has on customers’ future purchases. In our specific example, the coefficient for treatment was R$17.89 with a p-value < 0.01, while controlling for age and income. This indicates a significant effect of offering the coupon, although due to non-compliance, ITT will generally be lower than the true causal effect.

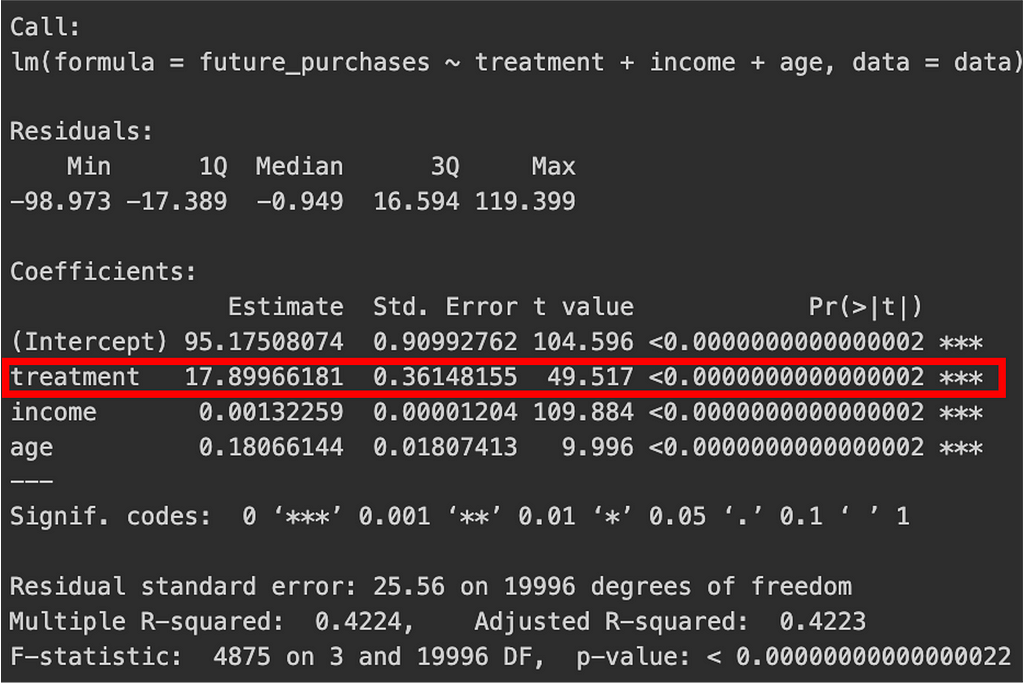
LATE estimate using IV: It represents the causal effect of coupon usage on future purchases among compliers (those who used the coupon because they received it). In our example, the estimated LATE was close to $50 (see the second figure in subsection “Verifying assumptions”), indicating that customers who complied by using the coupon saw their future purchases increase by roughly $50 compared to what would have happened without the coupon.

This result is larger than the ITT effect of R$17.89, as LATE focuses specifically on compliers, who are more likely to experience the true causal impact of using the coupon. Now you see how measuring LATE is important in experiments like this, helping us derive a more accurate understanding of the impact on individuals who actually use the treatment, and providing insights into the true efficacy of the intervention.

Just out of curiosity, run the following part of the script to learn that neither the difference in means between compliers and non-compliers, nor the difference between compliers and the control group, gives us the LATE simulated in the data — a point that many data professionals tend to overlook.

mean_compliers - mean_non_compliers # difference in means between compliers and non-compliers
mean_compliers - mean_control # difference in means between compliers and control

Insights to take home

Many data professionals focus only on the ITT estimate, often because it’s easier to explain or because they aren’t familiar with other estimands. However, the ITT effect can obscure the true impact on those who actually “consumed” the treatment. The LATE, on the other hand, provides a more accurate measure of the interventions effectiveness among compliers, offering insights that ITT alone cannot capture.

Although the instrumental variables (IV) approach may initially seem complex, random assignment in an experimental setup makes IV a powerful and reliable tool for isolating causal effects. Notice, however, that IV methods can also be applied beyond experimental contexts, provided the assumptions hold. For example, in a fuzzy regression discontinuity design (RDD), IV is a credible way to estimate local treatment effects, even though sharp RDD might appear more straightforward.

Thank you for reading. Follow me for more in this series 🙂

If you enjoyed this content and want to learn more about causal inference and econometrics, follow me here and on Linkedin, where I post about causal inference and career.

Would you like to support, me? Just share this with those who may be interested!

Recommended references

• Facure M. (2022). Causal Inference for the Brave and True, chapter 8 and chapter 9.
• Huntington-Klein N. (2021). The Effect: An Introduction to Research Design and Causality, chapter 19.

ITT vs LATE: Estimating Causal Effects with IV in Experiments with Imperfect Compliance was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.