Improving k-Means Clustering with Disentanglement

Learning the dataset class neighborhood structure improves clustering

An accompanying article for the paper “Improving k-Means Clustering with Disentangled Internal Representations” by A.F. Agarap and A.P. Azcarraga presented at the 2020 International Joint Conference on Neural Networks (IJCNN)

Background

Clustering is an unsupervised learning task that groups a set of objects in a way that the objects in a group share more similarities among them than those from other groups. It is a widely-studied task as its applications include but are not limited to its use in data analysis and visualization, anomaly detection, sequence analysis, and natural language processing.

Like other machine learning methods, clustering algorithms heavily rely on the choice of feature representation. In our work, we improve the quality of feature representation through disentanglement.

We define disentanglement as how far class-different data points from each other are, relative to class-similar data points. This is similar to the way the aforementioned term was treated in Frosst et al. (2019) So, maximizing disentanglement during representation learning means the distance among class-similar data points are minimized.

In doing so, it would preserve the class memberships of the examples from the dataset, i.e. how data points reside in the feature space as a function of their classes or labels. If the class memberships are preserved, we would have a feature representation space in which a nearest neighbor classifier or a clustering algorithm would perform well.

Clustering

Clustering is a machine learning task that finds the grouping of data points wherein the points in a group share more similarities among themselves relative to points in a different group.

Like other machine learning algorithms, the success of clustering algorithms relies on the choice of feature representation. One representation may be superior than another with respect to the dataset used. However, in deep learning, this is not the case since the feature representations are learned as an implicit task of a neural network.

Deep Clustering

And so, recent works such as Deep Embedding Clustering or DEC and Variational Deep Embedding or VADE in 2016, and ClusterGAN in 2018, took advantage of the feature representation learning capability of neural networks.

We will not discuss them in detail in this article, but the fundamental idea among these works is essentially the same, and that is to simultaneously learn the feature representations and the cluster assignments using a deep neural network. This approach is known as deep clustering.

Motivation

Can we preserve the class memberships of the data points in the dataset before clustering?

Although deep clustering methods learn the clustering assignment together with feature representations, what they do not explicitly set out to do is to preserve the class neighbourhood structure of the dataset. This serves as our motivation for our research, and that is can we preserve the class neighbourhood structure of the dataset and then perform clustering on the learned representation of a deep network.

In 2019, the Not Too Deep or N2D Clustering method was proposed wherein they learned a latent code representation of a dataset, in which they further searched for an underlying manifold using techniques such as t-SNE, Isomap, and UMAP. The resulting manifold is a clustering-friendly representation of the dataset. So, after manifold learning, they used the learned manifold as the dataset features for clustering. Using this approach, they were able to have a good clustering performance. The N2D is a relatively simpler approach compared to deep clustering algorithms, and we propose a similar approach.

Learning Disentangled Representations

We also use an autoencoder network to learn the latent code representation of a dataset, and then use the representation for clustering. We draw the line of difference on how we learn a more clustering-friendly representation. Instead of using manifold learning techniques, we propose to disentangle the learned representations of an autoencoder network.

To disentangle the learned representations, we use the soft nearest neighbour loss or SNNL which measures the entanglement of class-similar data points. What this loss function does is it minimizes the distances among class-similar data points in each of the hidden layer of a neural network. The work by Frosst, Papernot, and Hinton on this loss function used a fixed temperature value denoted by T. The temperature factor dictates how to control the importance given to the distances between pairs of points, for instance, at low temperatures, the loss is dominated by small distances while actual distances between widely separated representations become less relevant. They used SNNL for discriminative and generative tasks in their 2019 paper.

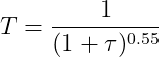
In our work, we used SNNL for clustering, and we introduce the use of an annealing temperature instead of a fixed temperature. Our annealing temperature is an inverse function with respect to the training epoch number which is denoted by τ.

Running a gradient descent on a randomly sampled and labelled 300 data points from a Gaussian distribution, we can see that using our annealing temperature for SNNL, we found faster disentanglement compared to using a fixed temperature. As we can see, even as early as the 20th epoch, the class-similar data points are more clustered together or entangled when using an annealing temperature than when using a fixed temperature, as it is also numerically shown by the SNNL value.

Our Method

So, our contributions are the use of SNNL for disentanglement of feature representations for clustering, the use of an annealing temperature for SNNL, and a simpler clustering approach compared to deep clustering methods.

Our method can be summarized in the following manner,

1. We train an autoencoder with a composite loss of binary cross entropy as the reconstruction loss, and the soft nearest neighbour loss as a regularizer. The SNNL for each hidden layer of the autoencoder is minimized to preserve the class neighbourhood structure of the dataset.
2. After training, we use the latent code representation of a dataset as the dataset features for clustering.

Clustering on Disentangled Representations

Our experiment configuration is as follows,

1. We used the MNIST, Fashion-MNIST, and EMNIST Balanced benchmark datasets. Each image in the datasets were flattened to a 784-dimensional vector. We used their ground-truth labels as the pseudo-clustering labels for measuring the clustering accuracy of our model.
2. We did not perform hyperparameter tuning or other training tricks due to computational constraints and to keep our approach simple.
3. Other regularizers like dropout and batch norm were omitted since they might affect the disentangling process.
4. We computed the average performance of our model across four runs, each run having a different random seed.

Clustering Performance

However, autoencoding and clustering are both unsupervised learning tasks, while we use SNNL, a loss function that uses labels to preserve the class neighbourhood structure of the dataset.

With this in mind, we simulated the lack of labelled data by using a small subset of the labelled training data of the benchmark datasets. The number of labelled examples we used were arbitrarily chosen.

We retrieved the reported clustering accuracy of DEC, VaDE, ClusterGAN, and N2D from literature as baseline results, and in the table above, we can see the summary of our findings where our approach outperformed the baseline models.

Note that these results are the best clustering accuracy among the four runs for each dataset since the baseline results from literature are also the reported best clustering accuracy by the respective authors.

Visualizing Disentangled Representations

To further support our findings, we visualized the disentangled representations by our network for each of the dataset.

For the EMNIST Balanced dataset, we randomly chose 10 classes to visualize for easier and cleaner visualization.

From these visualizations, we can see that the latent code representation for each dataset indeed became more clustering-friendly by having well-defined clusters as indicated by the cluster dispersion.

Training on Fewer Labelled Examples

We also tried training our model on fewer labelled examples.

In the figure above, we can see that even with fewer labelled training examples, the clustering performance on the disentangled representations is still on par with our baseline models from the literature.

This entails that in situations where labelled datasets is scarce, this method could be used to produce good results.

Conclusion

Compared to deep clustering methods, we employed a simpler clustering approach by using a composite loss of autoencoder reconstruction loss and soft nearest neighbor loss to learn a more clustering-friendly representation that improves the performance of a k-Means clustering algorithm.

Our expansion of the soft nearest neighbor loss used an annealing temperature which helps with faster and better disentanglement that helped improve the clustering performance on the benchmark datasets. Thus concluding our work.

Since the publication of our work, several other papers have built on the soft nearest neighbor loss, or were regarded to be quite similar. Most notably, the supervised contrastive (SupCon) learning paper from Google, but with the difference being the SupCon approach proposed normalization of embeddings, an increased use of data augmentation, a disposable contrastive head and two-stage training.

On the other hand, our work requires relatively lower hardware resources while achieving good results.

References

• Frosst, Nicholas, Nicolas Papernot, and Geoffrey Hinton. “Analyzing and improving representations with the soft nearest neighbor loss.” International conference on machine learning. PMLR, 2019.
• Goldberger, Jacob, et al. “Neighbourhood components analysis.” Advances in neural information processing systems. 2005.
• Khosla, Prannay, et al. “Supervised contrastive learning.” Advances in neural information processing systems 33 (2020): 18661–18673.
• Salakhutdinov, Ruslan, and Geoff Hinton. “Learning a nonlinear embedding by preserving class neighbourhood structure.” Artificial Intelligence and Statistics. 2007.

Improving k-Means Clustering with Disentanglement was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.