Handling feedback loops in recommender systems — Deep Bayesian Bandits

Handling Feedback Loops in Recommender Systems — Deep Bayesian Bandits

Understanding fundamentals of exploration and Deep Bayesian Bandits to tackle feedback loops in recommender systems

Introduction

Recommender system models are typically trained to optimize for user engagement like clicks and purchases. The well-meaning intention behind this is to favor items that the user has previously engaged with. However, this creates a feedback loop that over time can manifest as the “cold start problem”. Simply put, the items that have historically been popular for a user tend to continue to be favored by the model. In contrast, new but highly relevant items don’t receive much exposure. In this article, I introduce exploration techniques from the basics and ultimately explain Deep Bayesian Bandits, a highly-effective algorithm described in a paper by Guo, Dalin, et al [1].

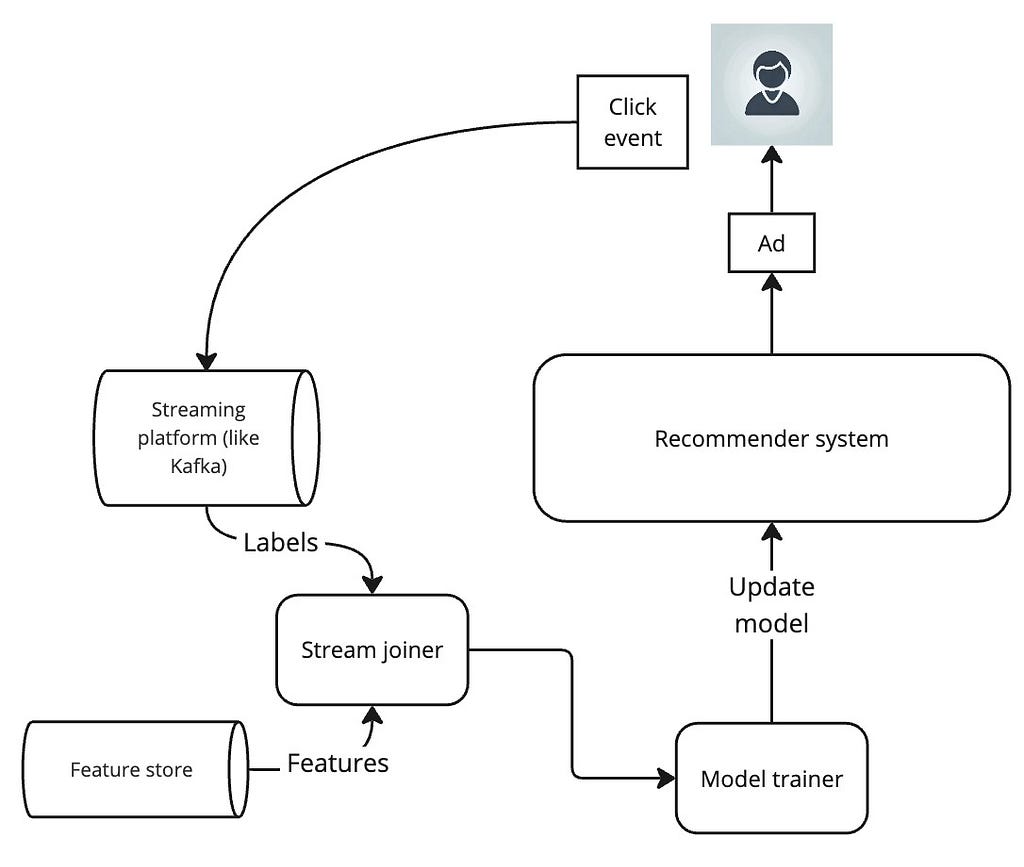
An ad recommender system

Let us use a simple ad recommender system as an example throughout this article.

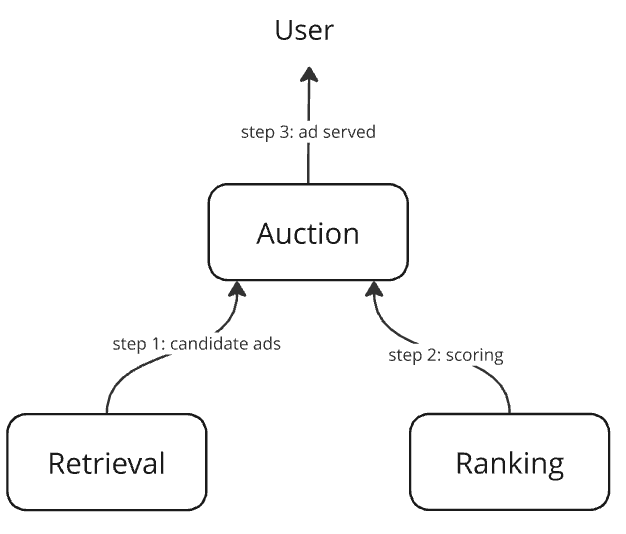
It is a three-component system

• Retrieval: a component to efficiently retrieve candidates for ranking
• Ranking: a deep neural network that predicts the click-through rate (CTR) as the score for an ad given a user
  score = predict_ctr(user features, ad features)
• Auction: a component that
  – retrieves candidate ads for the user
  – scores them using the ranking model
  – selects the highest-scored ad and returns it*

Our focus in this article will be exclusively on the ranking model.

*real-world auction systems also take the ad’s bid amount into account, but we ignore that for simplicity

Ranking model architecture

The ranking model is a deep neural network that predicts the click-through rate (CTR) of an ad, given the user and ad features. For simplicity, I propose a simple fully connected DNN below, but one could very well enrich it with techniques like wide-and-deep network, DCN, and DeepFM without any loss of applicability of the methods I explain in this article.

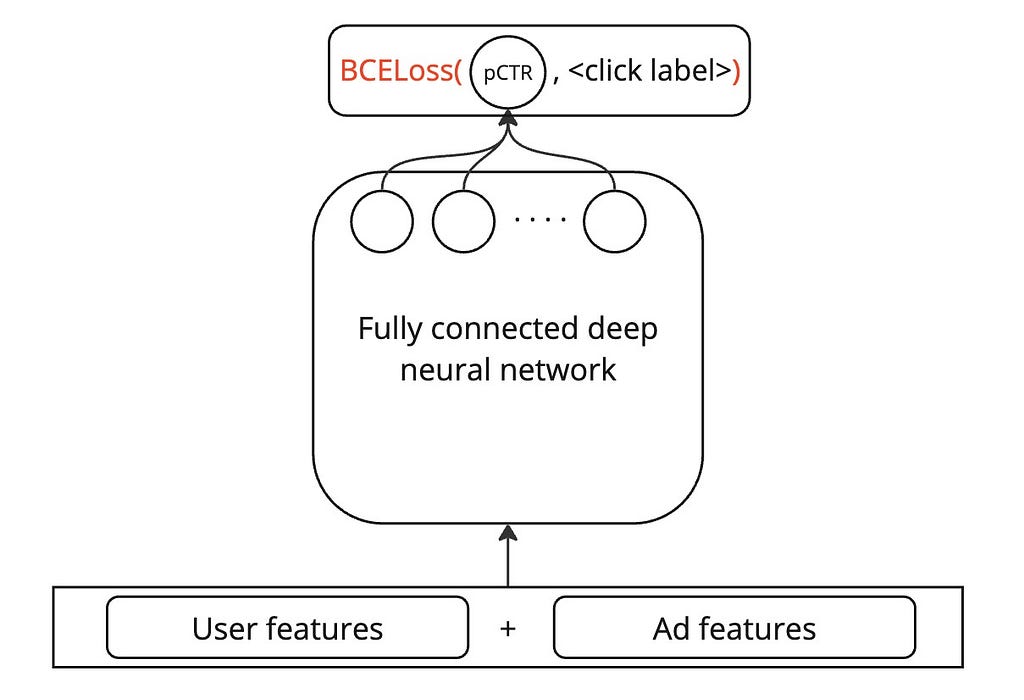
Training data

The ranking model is trained on data that comprises clicks as binary labels and, concatenation of user and ad features. The exact set of features used is unimportant to this article, but I have assumed that some advertiser brand-related features are present to help the model learn the user’s affinity towards brands.

The cold-start problem

Imagine we successfully trained our ranking model on our ads click dataset, and the model has learned that one of our users Jane loves buying bags from the bag company “Vogue Voyage”. But there is a new bag company “Radiant Clutch” in the market and they sell great bags. However, despite “Radiant Clutch” running ad campaigns to reach users like Jane, Jane never sees their ads. This is because our ranking model has so firmly learned that Jane likes bags from “Vogue Voyage”, that only their ads are shown to her. She sometimes clicks on them and when the model is further trained on these new clicks, it only strengthens the model’s belief. This becomes a vicious cycle leading to some items remaining in the dark.

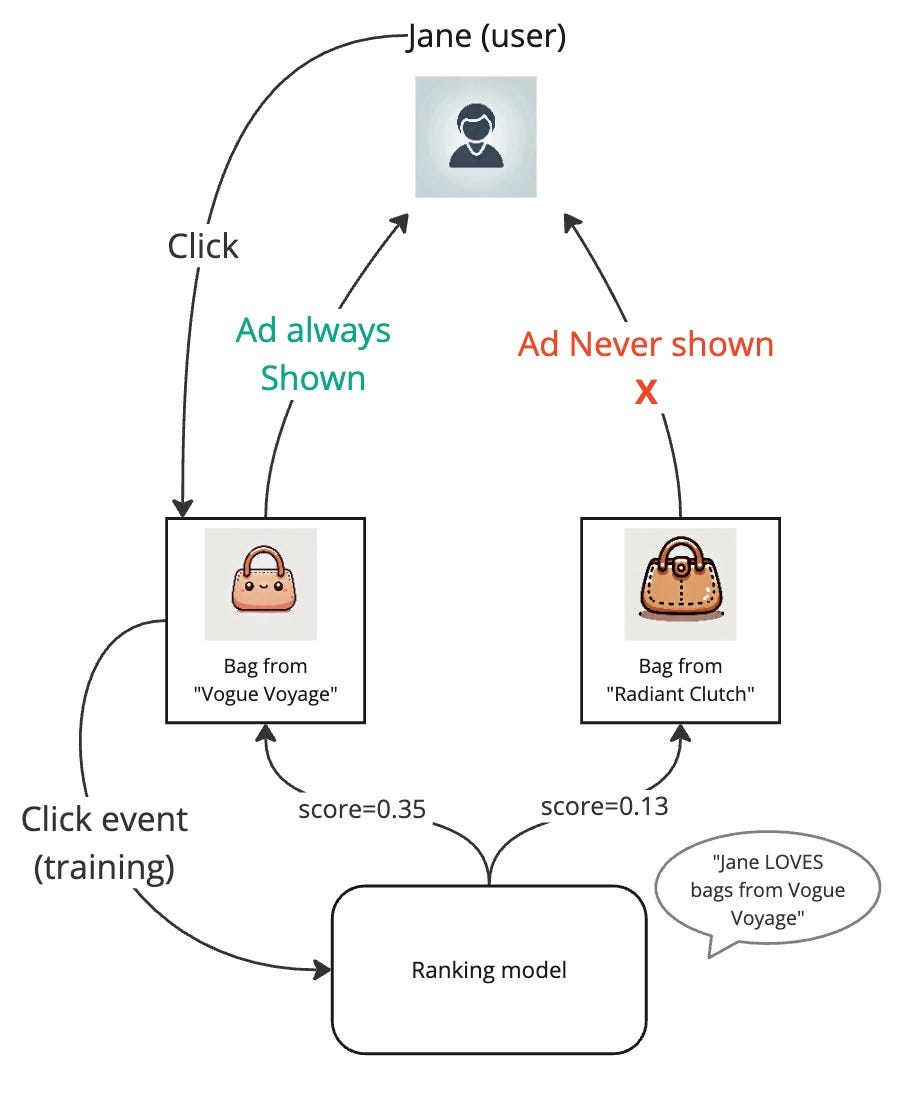
If we ponder about this, we’d realize that the model did not do anything wrong by learning that Jane likes bags from “Vogue Voyage”. But the problem is simply that the model is not being given a chance to learn about Jane’s interests in other companies’ bags.

Exploration vs exploitation

This is a great time to introduce the trade-off between exploration vs exploitation.

Exploitation: During ad auction, once we get our CTR predictions from our ranking model, we simply select the ad with the highest score. This is a 100% exploitation strategy because we are completely acting on our current best knowledge to achieve the greatest immediate reward.

Exploration: What our approach has been lacking is the willingness to take some risk and show an ad even if it wasn’t assigned the highest score. If we did that, the user might click on it and the ranking model when updated on this data would learn something new about it. But if we never take the risk, the model will never learn anything new. This is the motivation behind exploration.

Exploration vs exploitation is a balancing act. Too little exploration would leave us with the cold-start problem and too much exploration would risk showing highly irrelevant ads to users, thus losing user trust and money.

Exploration techniques

Now that we’ve set the stage for exploration, let us delve into some concrete techniques for controlled exploration.

ε-greedy policy

The idea here is simple. In our auction service, when we have the scores for all the candidate ads, instead of just taking the top-scored ad, we do the following

1. select a random number r in [0, 1)
2. if r < ε, select a random ad from our candidates (exploration)
3. else, select the top-scored ad (exploitation)

where ε is a constant that we carefully select in [0, 1) knowing that the algorithm will explore with ε probability and exploit with 1 — ε probability.

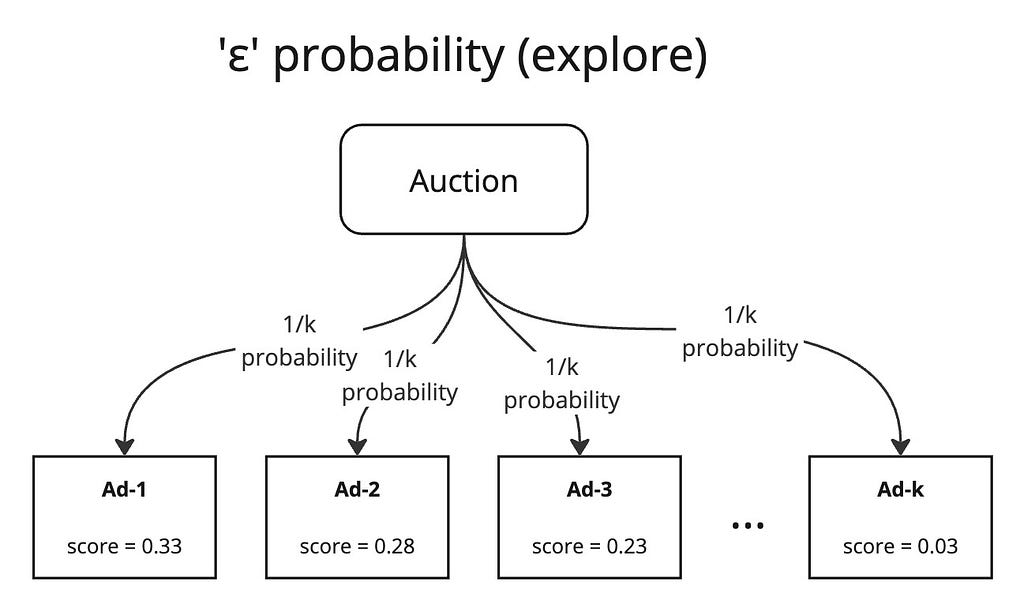
This is a very simple yet powerful technique. However, it can be too naive because when it explores, it completely randomly selects an ad. Even if an ad has an absurdly low pCTR prediction that the user has repeatedly disliked in the past, we might still show the ad. This can be a bit harsh and can lead to a serious loss in revenue and user trust. We can certainly do better.

Upper confidence bound (UCB)

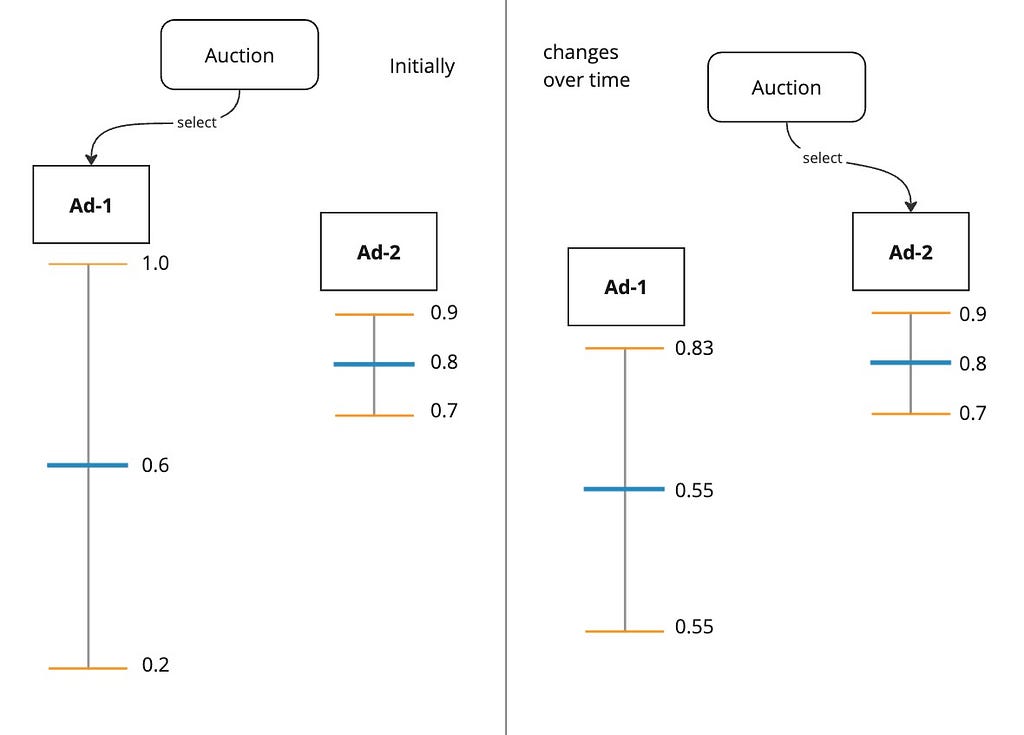
Our motivation for exploration was to ensure that all ad candidates have an opportunity to be shown to the user. But as we give some exposure to an ad, if the user still doesn’t engage with it, it becomes prudent to cut future exposure to it. So, we need a mechanism by which we select the ad based on both its score estimate and also the amount of exposure it has already received.

Imagine our ranking model could produce not just the CTR score but also a confidence interval for it*.

*how this is achieved is explained later in the article

Such a confidence interval is typically inversely proportional to the amount of exposure the ad has received because the more an ad is shown to the user, the more user feedback we have about it, which reduces the uncertainty interval.

During auction, instead of selecting the ad with the greatest pCTR, we select the ad with the highest upper confidence bound. This approach is called UCB. The philosophy here is “Optimism in the face of uncertainty”. This approach effectively takes into account both the ad’s score estimate and also the uncertainty around it.

Thompson sampling

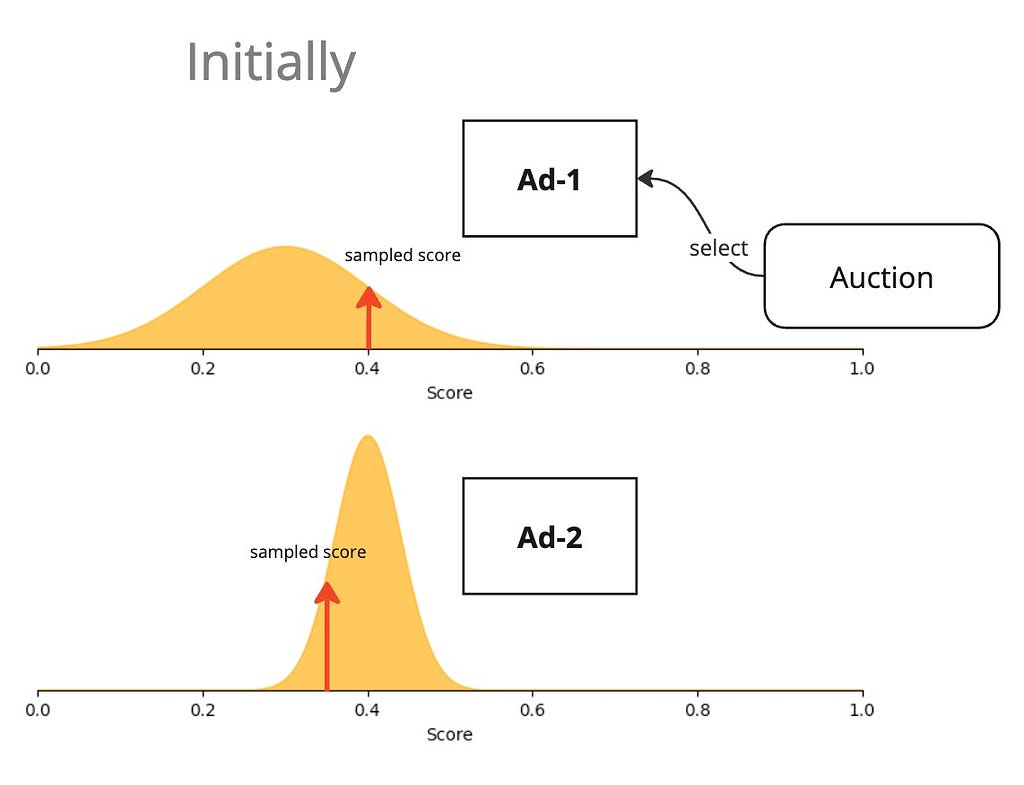
The UCB approach went with the philosophy of “(complete) optimism in the face of uncertainty”. Thompson sampling softens this optimism a little. Instead of using the upper confidence bound as the score of an ad, why not sample a score in the posterior distribution?

For this to be possible, imagine our ranking model could produce not just the CTR and the confidence interval but an actual score distribution*.

*how this is achieved is explained later in the article

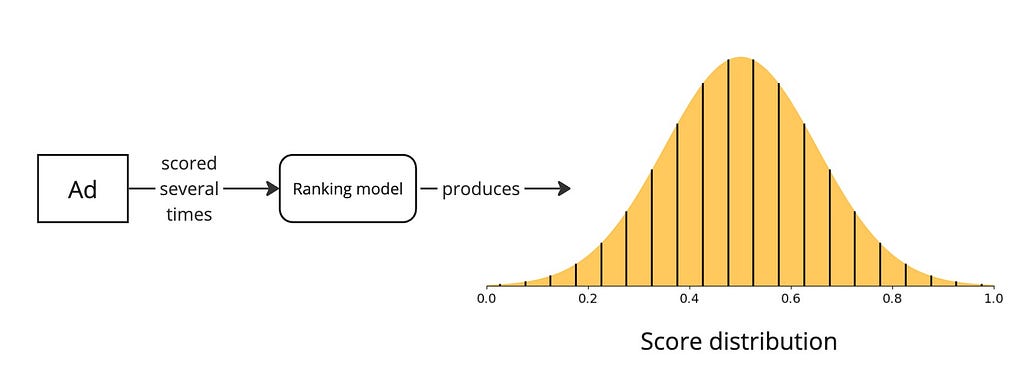
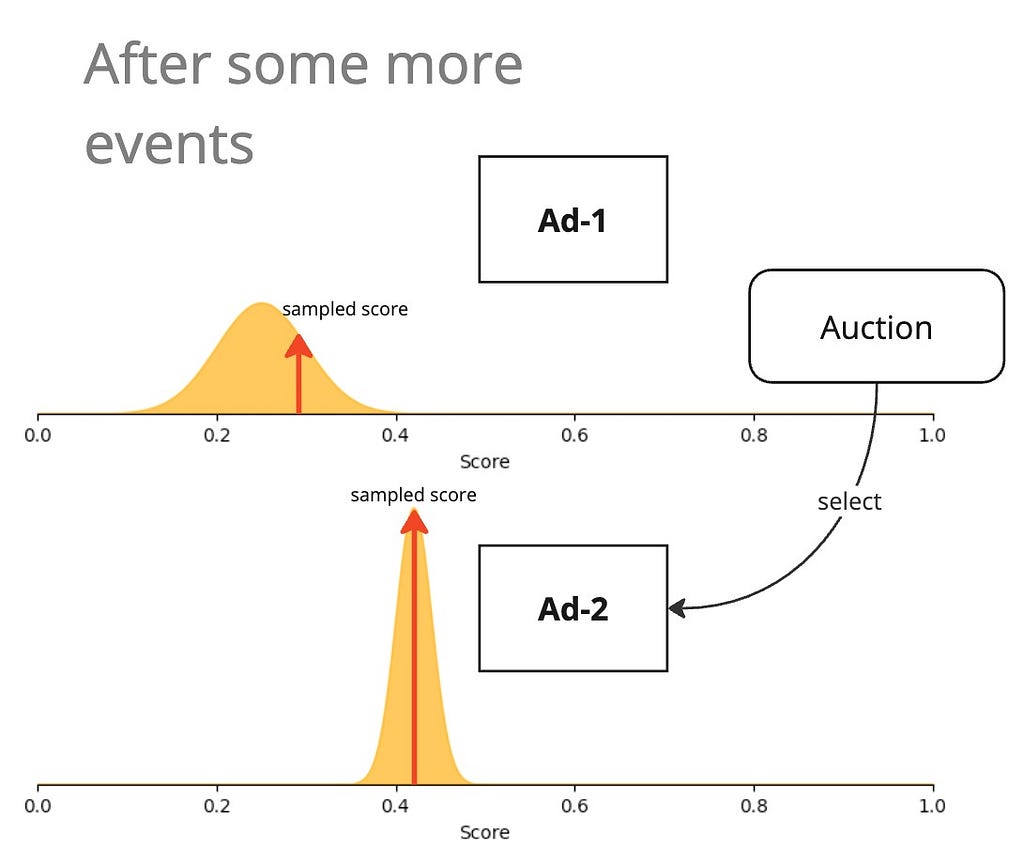
Then, we just sample a score from this distribution and use that as the score during auction.

Importance of updating the model

For the UCB and Thompson sampling techniques to work, we must update our models as often as possible. Only then will it be able to update its uncertainty estimates in response to user feedback. The ideal setup is a continuous learning setup where user feedback events are sent in near-real time to the model to update its weights. However, periodically statefully updating the weights of the model is also a viable option if continuous learning infrastructure is too expensive to set up.

Posterior approximation techniques

In the UCB and Thompson sampling approaches, I explained the idea of our model producing not just one score but an uncertainty measure as well (either as a confidence interval or a distribution of scores). How can this be possible? Our DNN can produce just one output after all! Here are the approaches discussed in the paper.

Bootstrapping

Bootstrapping in statistics simply means sampling with replacement. What this means for us is that we apply bootstrapping on our training dataset to create several closely related but slightly different datasets and train a separate model with each dataset. The models learned would thereby be slight variants of each other. If you have studied decision trees and bagging, you would already be familiar with the idea of training multiple related trees that are slight variants of each other.

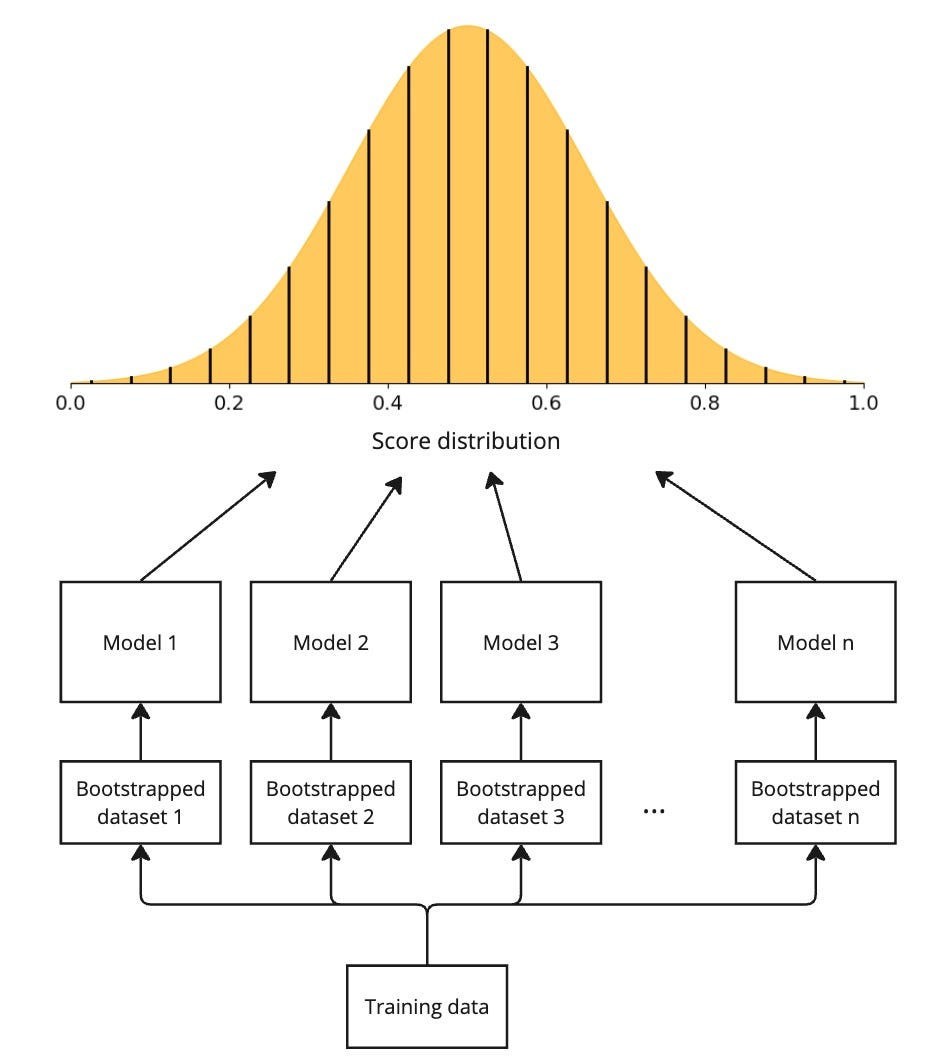
During auction, for each ad, we get one score from each bootstrapped model. This gives us a distribution of scores which is exactly what we wanted for Thompson sampling. We can also extract a confidence interval from the distribution if we choose to use UCB.

The biggest drawback with this approach is the sheer computational and maintenance overhead of training and serving several models.

Multi-head bootstrapping

To mitigate the costs of several bootstrapped models, this approach unifies the several models into one multi-head model with one head for each output.

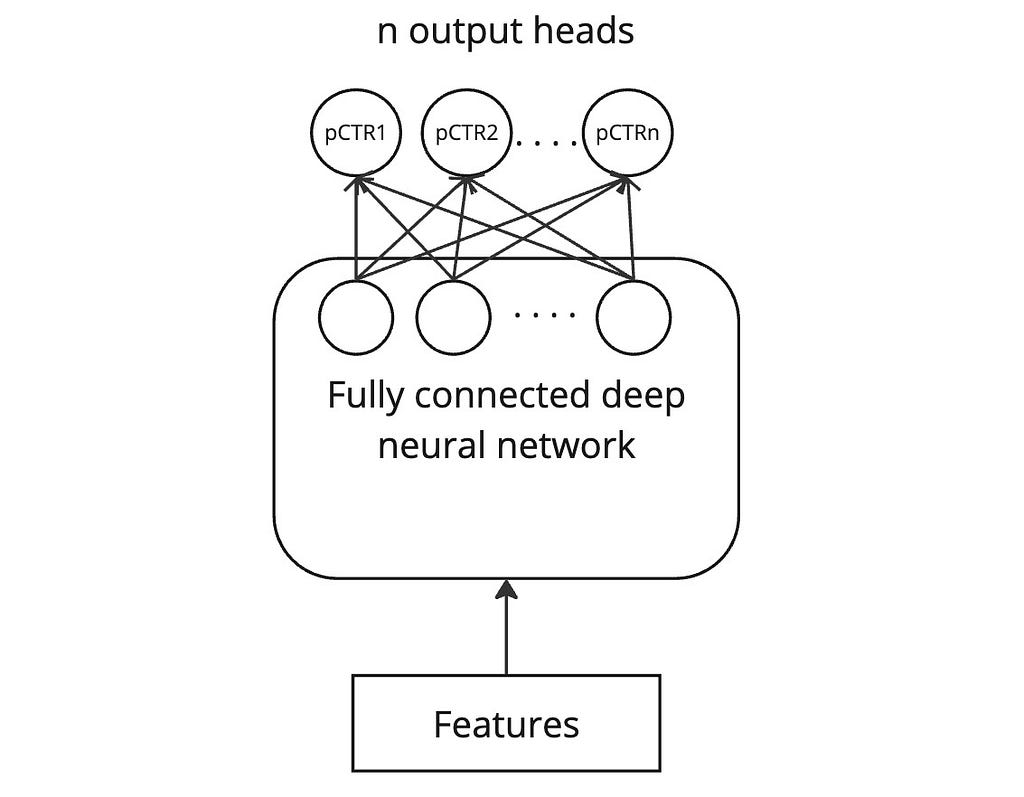
The key cost reduction comes from the fact that all the layers except the last are shared.

Training is done as usual on bootstrapped subsets of data. While each bootstrapped subset of data should be used to update the weights of all the shared layers, care must be taken to update the weight of just one output head with a subset of data.

Stochastic Gradient descent (SGD)

Instead of using separate bootstrapped datasets to train different models, we can just use one dataset, but train each model with SGD with random weight initialization thus utilizing the inherent stochasticity offered by SGD. Each model trained thus becomes a variant of the other.

Multi-head SGD

In the same way, using a multi-head architecture brought down the number of models trained with bootstrapping to one, we can use a multi-head architecture with SGD. We just have to randomly initialize the weights at each head so that upon training on the whole dataset, each head is learned to be a slight variant of the others.

Forward-propagation dropout

Dropout is a well-known regularization technique where during model training, some of the nodes of a layer are randomly dropped to prevent chances of overfitting. We borrow the same idea here except that we use it during forward propagation to create controlled randomness.

We modify our ranking model’s last layer to introduce dropout. Then, when we want to score an ad, we pass it through the model several times, each time getting a slightly different score on account of the randomness introduced by dropout. This gives us the distribution and confidence interval that we seek.

One significant disadvantage of this approach is that it requires several full forward passes through the network which can be quite costly during inference time.

Hybrid

In the hybrid approach, we perform a key optimization to give us the advantages of dropout and bootstrapping while bringing down the serving and training costs:

• With dropout applied to just the last-but-one layer, we don’t have to run a full forward pass several times to generate our score distribution. We can do one forward pass until the dropout layer and then do several invocations of just the dropout layer in parallel. This gives us the same effect as the multi-head model where each dropout output acts like a multi-head output.

Also, with dropout deactivating one or more nodes randomly, it serves as a Bernoulli mask on the higher-order features at its layer, thus producing an effect equivalent to bootstrapping with different subsets of the dataset.

Which approach works best?

Unfortunately, there is no easy answer. The best way is to experiment under the constraints of your problem and see what works best. But if the findings from the authors of the Deep Bayesian Bandits paper are anything to go by,

1. ε-greedy unsurprisingly gives the lowest CTR improvement due to its unsophisticated exploration, however, the simplicity and low-cost nature of it make it very alluring.
2. UCB generally outperformed Thompson sampling.
3. Bootstrap UCB gave the highest CTR return but was also the most computationally expensive due to the need to work with multiple models.
4. The hybrid model which relied on dropout at the penultimate layer needed more training epochs to perform well and was on par with SGD UCB’s performance but at lower computational cost.
5. The model’s PrAuc measured offline was inversely related to the CTR gain: this is an important observation that shows that offline performance can be easily attained by giving the model easier training data (for example, data not containing significant exploration) but that will not always translate to online CTR uplifts. This underscores the significance of robust online tests.

That said, the findings can be quite different for a different dataset and problem. Hence, real-world experimentation remains vital.

Conclusion

In this article, I introduced the cold-start problem created by feedback loops in recommender systems. Following the Deep Bayesian Bandits paper, we framed our ad recommender system as a k-arm bandit and saw many practical applications of reinforcement learning techniques to mitigate the cold-start problem. We also scratched the surface of capturing uncertainty in our neural networks which is a good segue into Bayesian networks.

[1] Guo, Dalin, et al. “Deep bayesian bandits: Exploring in online personalized recommendations.” Proceedings of the 14th ACM Conference on Recommender Systems. 2020.

Handling feedback loops in recommender systems — Deep Bayesian Bandits was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.