Using a GloVe embedding-based algorithm to achieve 100% accuracy on the popular party game “Codenames”
Introduction
Codenames is a popular party game for 2 teams of 2 players each, where each team consists of a spymaster and an operative. Each team is allocated a number of word cards on a game board. During each turn, the spymaster provides a word clue, and the number of word cards it corresponds to. The operative would then have to guess which words on the game board belong to his/her team. The objective is for the spymaster to provide good clues, such that the operative can use fewer number of turns to guess all the words, before the opponent team. In addition, there will be an “assassin” card, which upon being chosen by the operative, causes the team to lose immediately.
In this project, we are going to use a simple word vector algorithm using pre-trained word vectors in machine learning to maximize our accuracy in solving the game in as few tries as possible.
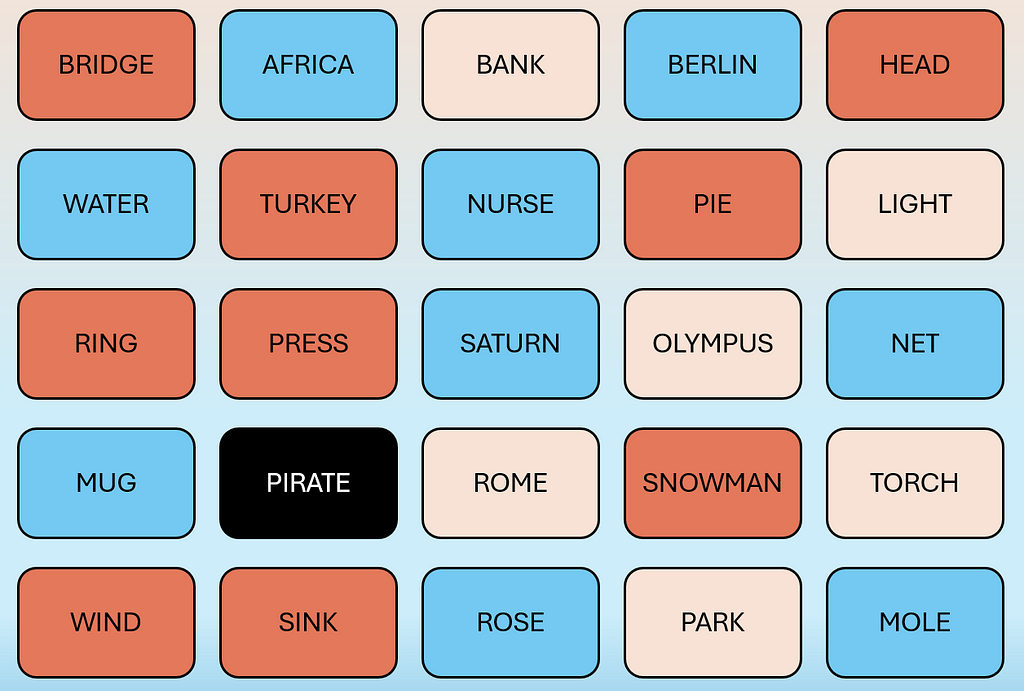
Below are examples of what the game board looks like:


In the card arrangement for the Spymaster, the color of each card represents Red Team, Blue Team, Neutral (Beige) and Assassin Card (Black).
Automating the spymaster and operative
We will be creating an algorithm that can take on both the roles of spymaster and operative and play the game by itself. In a board of 25 cards, there will be 9 “good” cards and 16 “bad” cards (including 1 “assassin” card).
Representing meaning with GloVe embeddings
In order for the spymaster to give good clues to the operative, our model needs to be able to understand the meaning of each word. One popular way to represent word meaning is via word embeddings. For this task, we will be using pre-trained GloVe embeddings, where each word is represented by a 100-dimensional vector.
We then score the similarity between two words using cosine similarity, which is the dot product of two vectors divided by their magnitudes:

Operative: Decoding Algorithm
During each turn, the operative receives a clue c, and an integer n representing the number of corresponding words to guess. In other words, the operator has to decode a {c, n} pair and choose n words one at a time without replacement, until a wrong word is reached and the turn ends.
Our decoder is a straightforward greedy algorithm: simply sort all the remaining words on the board based on cosine similarity with the clue word c, and pick the top n words based on similarity score.
Spymaster: Encoding Algorithm
On each turn, based on the remaining “good” and “bad” words, the spymaster has to pick n words and decide on a clue c to give to the operative. One assumption we make here is that the spymaster and operative agree on the decoding strategy mentioned above, and hence the operator will pick the optimal {c, n} that will maximize the number of correct words chosen.
At this point, we can make an observation that the clue c is an information bottleneck, because it has to summarize n words into a single word c for the operative to decode. The word vector of the encoded clue lies in the same vector space as each of the original word vectors.

Generating clue candidates
Word embeddings have the property of enabling us to represent composite meanings via the addition and subtraction of different word vectors. Given set of “good” words G and set of “bad” words B, we can use this property to obtain an “average” meaning of a “good” word, with reference to the “bad” words, by computing a normalized mean of the vectors, with “good” word vectors being added, and “bad” word vectors being subtracted. This average vector enables us to generate clue candidates:
glove = api.load("glove-wiki-gigaword-100")
good_words = [g_1, g_2, ..., g_n]
bad_words = [b_1, b_2, ..., b_n]
candidates = glove.most_similar(positive=good_words,negative=bad_words,topn=20)
Negative sampling
As the number of “bad” words usually exceeds the number of “good” words, we perform negative sampling, by randomly sampling an equal number of “bad” words compared to the “good” words in our computation of our average word vector. This also contributes to more randomness in the clues generated, which improves the diversity of clue candidates.
After we find the average word vector, we use the most_similar() function in Gensim to obtain the top closest words from the entire GloVe vocabulary with respect to the average word vector, based on cosine similarity.
Score function
Now, we have a method to generate candidates for clue c, given n words. However, we still have to decide which candidate c to pick, which n words to choose, and how to determine n.
Thereafter, we generate all possible combinations of k, k-1, …, 1 words from the k “good” words remaining on the board, as well as their respective clue word candidates c, working backwards from k. To pick the best {c, n}, we score all the candidates from each possible combination of the remaining “good” words, through the decoding algorithm. Then we obtain the maximum number of words guessed correct given clue c, count(c), since we know what strategy the operative will use.

Results
In each game, 25 words are sampled from a list of 400 common Codenames words. Overall, after 100 experiments, our method chooses the correct word 100% of the time, completing the game within an average of 1.98 turns, or 4.55 guesses per turn (for 9 correct words), taking at most 2 turns.

In other words, this algorithm takes two turns almost every game, except for a few exceptions where it guesses all the words in a single turn.
Let’s view a sample distribution of word embeddings of the clues and guesses we made.

Although the clues generated do provide some level of semantic summary of the words that the operative eventually guessed correctly, these relationships between clues and guesses may not be obvious from a human perspective. One way to make to clues more interpretable is to cap the maximum number of guesses per turn, which generates clues with better semantic approximation of the guesses.
Even so, our algorithm promotes a good clustering outcome for each of the words, to enable our decoder to get more words correct by providing good clues that lie close to the target words.
Conclusion
In conclusion, this greedy GloVe-based algorithm performs well as both the spymaster and operative in the Codenames game, by offering an effective way to encode and decode words via a clue and number.
In our model, the encoder and decoder share a common strategy, which works in similar ways as a shared encryption key. A possible limitation of this is that the encoder and decoder will not work as well separately, as a human player may not be able to interpret the generated clues as effectively.
Understanding the mechanics behind word embeddings and vector manipulation is a great way to get started in Natural Language Processing. It is interesting to see how simple methods can also perform well in such semantic clustering and classification tasks. To enhance the gameplay even further, one can consider using adding elements of reinforcement learning or training an autoencoder to achieve better results.
Github Repository: https://github.com/jzh001/codenames
References
- Koyyalagunta, D., Sun, A., Draelos, R. L., & Rudin, C. (2021). Playing codenames with language graphs and word embeddings. Journal of Artificial Intelligence Research, 71, 319–346. https://doi.org/10.1613/jair.1.12665
- Pennington, J., Socher, R., & Manning, C. (2014). Glove: Global vectors for word representation. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). https://doi.org/10.3115/v1/d14-1162
- Li, Y., Yan, X., & Shaw, C. (2022). Codenames AI https://xueweiyan.github.io/codenames-ai-website/
- Friedman, D., & Panigrahi, A. (2021). Algorithms for Codenames https://www.cs.princeton.edu/~smattw/Teaching/521FA21/FinalProjectReports/FriedmanPanigrahi.pdf
- Jaramillo, C., Charity, M., Canaan , R., & Togelius, J. (2020). Word Autobots: Using Transformers for Word Association in the Game Codenames. Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, 16(1), 231–237. https://doi.org/10.1609/aiide.v16i1.7435
Hacking “Codenames” with GloVe Embeddings was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Hacking “Codenames” with GloVe Embeddings
Go Here to Read this Fast! Hacking “Codenames” with GloVe Embeddings