Galactic Distances

How Far Are We from Alien Civilizations? (Part 4 of the Drake Equation Series)

Recap:

In our journey so far, we’ve walked through the Drake Equation to estimate how many civilizations might be “out there” in our galaxy. We’ve covered the stars, the planets that could support life, and how many might develop intelligent civilizations. In Part 3, we estimated how many of those civilizations are capable of communicating with us right now. Now, in Part 4, we’re facing the big question: How far away are they?

The Milky Way is vast. We know there could be thousands of civilizations out there, but the galaxy is 100,000 light-years across — so even if they exist, could we ever hear from them? This article explores the mind-bending distances between us and these potential civilizations, and what that means for our search for extraterrestrial life.

How Big is Space? Putting the Vastness of the Milky Way into Perspective

To put the vastness of space into perspective, let’s start by imagining the Milky Way galaxy, which spans about 100,000 light-years in diameter. Now, if we were to shrink the galaxy down to the size of Earth (with a diameter of about 12,742 kilometers), the relative size of Earth itself would become unimaginably small. In fact, Earth would be 742 billion times smaller in comparison — about the size of a single human red blood cell. This comparison illustrates just how immense our galaxy is and emphasizes the monumental challenge of exploring or communicating across such vast distances. Imagine the difficulty of trying to find a single red blood cell in a space the size of the Earth!

Step 8: Estimating the Distance to the Nearest Alien Civilization

The results from Part 3 suggested that there could be up to 2,363 alien civilizations communicating in our galaxy right now. But what does that mean in practical terms? If they’re out there, how close is the nearest one?

Why This Step Matters

Even if we know there are thousands of civilizations, distance is a huge hurdle. The farther away they are, the harder it is to detect their signals — or for them to detect ours. If we want to set realistic expectations for contacting these civilizations, we need to know how far away they are. And if they’re hundreds or even thousands of light-years away, it’s going to be tough to communicate in real time. Imagine sending a text, only to get a reply 2,000 years later!

Our Approach

We’re assuming that alien civilizations are randomly distributed throughout the Milky Way. This gives us a nice, even spread across the galaxy’s disk, which has a diameter of around 100,000 light-years and a thickness of 1,300 light-years.

This approach keeps things simple while acknowledging that we’re making some big assumptions. For example, we’re not considering galactic zones that might be more “life-friendly,” and we’re ignoring the idea that some regions might be barren. But for our purposes, this model gives us a solid foundation for calculating the average distance to the nearest civilization.

Code for Step 8: Calculating the Distance to the Nearest Alien Civilization

***********************************************************************
*Calculate the distance to the closest civilization assuming that they 
*are randomly distributed across the galaxy
***********************************************************************

data closest_civilization;
/* Set seed for reproducibility */
  call streaminit(123);

/* Define Parameters */
  %let num_civilizations = 2363;
  %let num_iterations = 100;

  %let galactic_radius = 50000;
  %let galactic_height = 1300;

/* Initialize variables */
  length iteration 8 distance 8;
  array distances[&num_iterations]

/* Calculate distances */
  do i = 1 to &num_iterations;
/* Generate random coordinates for civilizations */
    do j = 1 to &num_civilizations;
      x = rand("Uniform", -&galactic_radius, &galactic_radius);     
      y = rand("Uniform", -&galactic_radius, &galactic_radius);
      z = rand("Uniform", -&galactic_height, &galactic_height);

/* Calculate distance from Earth */
      distance = sqrt(x**2 + y**2 + z**2)

/* Update closest distance if applicable */
      if j = 1 then closest_distance = distance;    
      else if distance < closest_distance then closest_distance = distance; 
    end;

/* Store closest distance */
    distances[i] = closest_distance;  
  end;

/* Output distances to dataset */
  do iteration = 1 to &num_iterations;
    distance = distances[iteration];
    output;
  end;

/* Keep only the necessary variables */
  keep iteration distance;
run;

A Small Confession: I Cheated (and Gave Us Better Odds)

Alright, time for a little confession: the Earth isn’t actually sitting in the middle of the galaxy, despite how I set up the code to calculate the distance to the nearest alien civilization. In reality, we’re about three-quarters of the way toward the edge of the Milky Way. If I had placed the Earth where it truly belongs, the average distance to alien civilizations on the far side of the galaxy would be much greater. But by “cheating” and moving us to the galactic center, I’ve inadvertently decreased the average distance to potential neighbors — and, in turn, increased our odds of contact. So yes, this biased approach works in our favor, but I’m sure you won’t mind if I made the cosmos feel a little cozier!

Breaking Down the Code: Calculating the Distance to the Nearest Civilization

This code is designed to simulate and calculate the distance from Earth to the nearest alien civilization, assuming that civilizations are randomly distributed throughout the Milky Way galaxy. Let’s walk through the key components and logic of the code.

Overview of the Key Variables

• num_civilizations: This is set to 2,363, which is the number of civilizations we estimated in Part 3 to be communicating at the same time as us. This parameter is the foundation of our calculation, as we want to figure out how far the closest of these civilizations might be from us.
• galactic_radius and galactic_height: These parameters define the size of the Milky Way. The galaxy is modeled as a disk, 100,000 light-years in diameter (which gives us a radius of 50,000 light-years) and 1,300 light-years thick.
• num_iterations: The code will run 100 iterations of the simulation, meaning it will randomly distribute the civilizations and recalculate the distance multiple times to get a range of possible distances to the nearest civilization.

Setting Up the Simulation

• Random Seeding (call streaminit(123)): This is for reproducibility. By setting a seed value (123), we ensure that every time we run this code, we get the same random values, making the results consistent across multiple runs.
• Random Galactic Coordinates: Each alien civilization is randomly placed in the galaxy by generating random (x, y, z) coordinates, with x and y representing the positions within the galaxy’s disk (radius), and z representing the position relative to the height of the galaxy (its thickness). The rand(“Uniform”,…) function generates random values within the specified ranges:
• The x and y coordinates are picked from a range of -50,000 to +50,000 light-years to cover the full width of the galaxy.
• The z coordinate is picked from a range of -1,300 to +1,300 light-years to represent the galaxy’s thickness.

Calculating Distance from Earth

The next section of the code calculates the distance from Earth (located at the origin, [0, 0, 0]) to each randomly positioned alien civilization using the 3D distance formula:

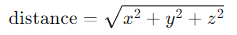
This formula calculates the straight-line distance from Earth to each civilization based on its random galactic coordinates.

Finding the Closest Civilization

Now that we have the distances, the code checks which one is the closest:

• First Civilization: On the first iteration (when j = 1), the first calculated distance is stored as the closest distance, because at this point, there’s nothing to compare it to.
• Subsequent Civilizations: For each additional civilization, the code compares its distance to the previously stored closest distance. If the new distance is smaller, it updates the value of closest_distance.

Storing and Outputting the Results

• Storing the Closest Distance: The closest distance found in each iteration is stored in the array distances[]. This allows us to keep track of the closest civilization for each simulation run.
• Output the Distances: The do loop at the end outputs the distance data for each iteration, so we can analyze the distribution of these results. It’s essentially producing a dataset of distances for all 100 simulation runs.

What This Code Is Doing

This simulation is creating random galactic coordinates for 2,363 civilizations in each iteration, calculating the distance to Earth for each one, and identifying the closest civilization. It repeats this process 100 times, giving us a range of possible distances to the nearest alien civilization based on the assumptions we’ve made.

Why This Matters

This is a crucial step in understanding the practical challenge of contacting extraterrestrial civilizations. Even if there are thousands of civilizations, the closest one could still be far beyond our reach. By simulating random distributions, we get an idea of the minimum distance we’d need to cover to contact another civilization — which sets realistic expectations for the search for extraterrestrial life.

Output and Explanation: Distance to the Nearest Civilization

Now for the results! After running the simulation, we get the following estimates for the distance to the nearest alien civilization, based on our earlier calculations:

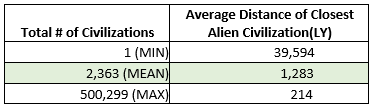
• Minimum Number of Civilizations (1): 39,594 light-years away.
• Mean Number of Civilizations (2,363): 1,283 light-years away.
• Maximum Number of Civilizations (500,299): 214 light-years away.

What Does This Tell Us?

• The Closest Possible Civilization: If we take the optimistic scenario where there are half a million alien civilizations, the nearest one would be just over 200 light-years away. This is within a range that we could theoretically detect with current technology, but it’s still a long shot.
• The Most Likely Scenario: With our mean estimate of 2,363 civilizations, the nearest one is likely around 1,283 light-years away. For perspective, that means a signal we send today wouldn’t reach them for over a millennium — and we wouldn’t get a reply until another millennium had passed!
• The Worst-Case Scenario: If there’s only one other civilization out there, it could be nearly 40,000 light-years away, making contact almost impossible.

Why This Matters

Even with the exciting possibility of thousands of alien civilizations, the sheer distances between us are daunting. On average, we’re looking at over 1,000 light-years to the nearest civilization, which means that communication is a long shot — at least with our current technology. But that doesn’t mean the search is hopeless. It just means we need to adjust our expectations and think about more indirect ways to detect signs of intelligent life.

Step 9: Traveling the Cosmic Distances — The Role of Relativity

So, let’s say we somehow knew where an alien civilization was located. How long would it take to reach them? This is where things get even more mind-bending — because when you’re talking about interstellar distances, you have to think about Einstein’s theory of special relativity.

Understanding the Lorentz Factor

At the heart of special relativity is the Lorentz Factor. This concept explains how time and space behave as objects approach the speed of light, and it’s key to understanding how interstellar travel might work.

Here’s the formula:

Where:

• v is the velocity of the spacecraft (or any object moving through space).
• c is the speed of light.

What this equation tells us is that as an object’s velocity v gets closer to the speed of light c, the Lorentz Factor γ grows larger. This leads to two key effects:

• Time Dilation: Time slows down for the travelers on the spacecraft. If you’re zooming through space at close to light speed, you experience less time than those on Earth. So, a trip that takes thousands of years from Earth’s perspective might only feel like a few years to the travelers.
• Length Contraction: The distance to your destination appears shorter. As you approach the speed of light, distances seem to shrink for the people on the spacecraft.

Now, let’s apply this to our scenario.

Code for Step 9: Calculating Travel Time and the Lorentz Factor

***************************************************************;
*How long is the travel time given different distances and     ;
*different "% of speed of light"                               ;
***************************************************************;

/* Constants */
data _null_;
    speed_of_light = 299792.458; /* km/s */
    distance_ly = 100; /* Light years */
    distance_km = distance_ly * 9.461 * 10**12; /* Conversion to kilometers */
    travel_distance = distance_km;
    travel_time = travel_distance / (0.9 * speed_of_light); /* Convert to seconds and reduce top speed of ship 
                  to % of the speed of light*/

    put "Travel Distance (km): " distance_km;
    put "Travel Time (seconds): " travel_time;

    velocity = travel_distance / travel_time;

    lorentz_factor = 1 / sqrt(1 - (velocity**2 / (speed_of_light**2)));
    proper_time_sp = travel_time / lorentz_factor; /* unit of time experienced on spaceship */
    time_dilation_sp = proper_time_sp / (365.25 * 24 * 60 * 60); /* converting to years */
    time_earth = travel_time / (365.25 * 24 * 60 * 60); /* converting to years */

    put "Velocity: " velocity;
    put "Lorentz Factor: " lorentz_factor;
    put "Proper Time (Spaceship): " proper_time_sp " seconds";
    put "Time Dilation (Spaceship): " time_dilation_sp " years";
    put "Time (Earth): " time_earth " years";
run;

Breaking Down the Code: Calculating Travel Time and Time Dilation

This code is designed to calculate how long it would take a spacecraft to travel between Earth and the nearest alien civilization at a fraction of the speed of light. It also calculates the time dilation experienced by the travelers due to Einstein’s theory of special relativity. Let’s break it down step by step to understand how these calculations work and why they’re important.

Constants and Basic Calculations

1. Speed of Light:

• The speed of light, denoted as speed_of_light, is a well-known constant set at 299,792.458 km/s. This is the maximum speed limit for any object according to the laws of physics, and it forms the basis for our travel calculations.

2. Distance to the Closest Civilization:

• We set the distance to the nearest civilization (distance_ly) at 1,283 light years (a placeholder value). This number represents the distance we estimated in earlier steps, based on the distribution of civilizations.

3. Convert Distance to Kilometers:

• Since the speed of light is in km/s, we need to convert the distance from light years to kilometers:

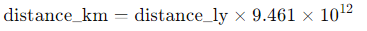
A light year is approximately 9.461 trillion kilometers, so this conversion gives us the total distance in kilometers, which is crucial for the travel time calculation.

Calculating Travel Time

1. Fraction of the Speed of Light:

• The example below calculates the travel time based on a ship traveling at 1% of the speed of light. The formula used for travel time is:

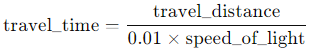
This formula converts the total distance to the time it would take the spacecraft to cover that distance at 1% of the speed of light. The output is in seconds, which gives us the most precise calculation.

2. Print Travel Distance and Time:

• The program outputs the total distance (in kilometers) and travel time (in seconds) to give us a sense of the scale we’re dealing with.

Special Relativity and Time Dilation

In this part of the code, we’re revisiting Einstein’s theory of special relativity, focusing on time dilation as it relates to interstellar travel. We previously discussed the Lorentz Factor, which plays a crucial role in determining how time slows down for objects moving at speeds close to the speed of light.

But why are we using the Lorentz Factor here?

Why the Lorentz Factor Matters

In the context of interstellar travel, as a spacecraft’s velocity approaches the speed of light, the Lorentz Factor increases dramatically. This has two significant effects:

1. Time Dilation: The time experienced by the crew aboard the spacecraft would be much shorter than the time experienced by observers on Earth. In essence, while the journey might take centuries or millennia from Earth’s perspective, only a few years could pass for the crew.
2. Perception of Distance: The faster the spacecraft travels, the shorter the distance appears to those on board. This contraction of space, caused by the Lorentz Factor, means that the crew would perceive the journey as much shorter than the actual distance across space.

Impact on Travel Time

By incorporating the Lorentz Factor, the code allows us to calculate two important results:

• Proper Time on the Spaceship: The amount of time the crew would experience while traveling across vast distances. Thanks to time dilation, this will be significantly shorter than the time that passes on Earth.
• Time on Earth: The total time it would take from an Earth-bound perspective to reach a distant alien civilization. Even at high speeds, the journey could span centuries or longer.

This is why the Lorentz Factor is critical: it lets us understand how time and space behave at relativistic speeds, giving us a glimpse into the effects that would make long-distance space travel more manageable for the travelers, though still incredibly challenging from an Earth-bound perspective.

Final Output

The code outputs several key insights:

• Velocity: The spacecraft’s speed as it approaches a percentage of the speed of light.
• Lorentz Factor: How much time dilation is occurring due to the spacecraft’s speed.
• Proper Time: The journey’s duration as experienced by the crew.
• Time on Earth: How much time would pass for those remaining on Earth while the journey is undertaken.

Why This Matters

This section highlights the staggering complexity of interstellar travel. Even though the crew would experience a much shorter journey thanks to time dilation, the distance between Earth and potential alien civilizations remains immense. The Lorentz Factor illustrates how the laws of physics influence not only the speed of travel but also the perception of time and distance. While time dilation offers a potential advantage for long-distance voyages, the journey to a distant civilization remains a monumental task, requiring technology far beyond what we currently possess.

Output and Explanation: Traveling the Cosmic Distances

Now, we’ve come to the moment of truth — understanding just how long it would take to reach the nearest alien civilization given the vast distances of space and different travel speeds.

Travel Time to the Nearest Civilization

We’ve assumed that the nearest alien civilization is 1,283 light-years away, based on our earlier estimates. Here’s where things get fascinating. The travel time varies dramatically depending on how fast the spacecraft is traveling relative to the speed of light. Let’s explore these numbers:

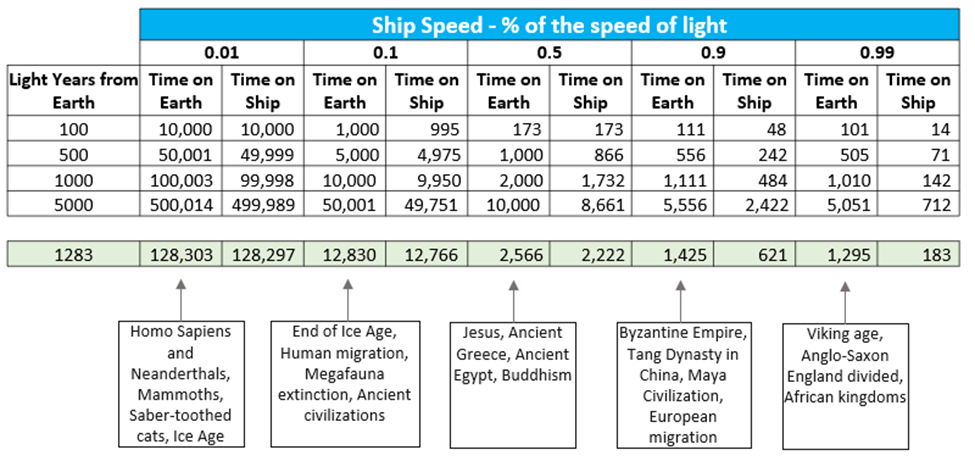
• At 1% the Speed of Light: The journey would take a staggering 128,303 years from Earth’s perspective. To put that into context, Homo sapiens would have been living alongside Neanderthals and saber-toothed cats during the Ice Age if this trip had started that long ago!
• At 10% the Speed of Light: The trip would still take 12,830 years from Earth’s point of view — that’s around the time of the end of the Ice Age, when humans began migrating and megafauna like mammoths were going extinct.
• At 50% the Speed of Light: We start seeing more manageable numbers. The journey would take 2,566 years from Earth’s perspective, which means that when the spacecraft left, humanity would have been in the time of Jesus, ancient Greece, Egypt, and the rise of Buddhism.
• At 90% the Speed of Light: Now we’re getting somewhere! The trip would take 1,425 years from Earth’s perspective. Think about that: when the travelers set off, the Byzantine Empire was at its height, the Tang Dynasty ruled China, and the Maya civilization was flourishing.
• At 99% the Speed of Light: The journey now takes just 1,295 years from Earth’s perspective. To put that in context, Vikings were sailing the seas, and Anglo-Saxon kingdoms were being established in what is now England.

But there’s more. These figures show time from Earth’s point of view, but for the astronauts on the spacecraft, time dilation caused by traveling at near-light speeds means they’ll experience much less time passing.

Why Time Dilation is Crucial

As the spacecraft approaches the speed of light, time dilation becomes an extraordinary advantage for the travelers:

• At 50% the Speed of Light, while 2,566 years would pass on Earth, the crew would only experience 2,222 years.
• At 90% the Speed of Light, while 1,425 years would pass on Earth, the crew would only feel 621 years passing. That’s enough for the journey to span multiple human generations, but it makes the idea of interstellar travel more feasible — at least for those aboard the spacecraft.
• At 99% the Speed of Light, this becomes even more dramatic. While the journey would take 1,295 years from Earth’s perspective, the crew would only experience 183 years.

The effect of time dilation means that, for the crew, the journey might feel much shorter, even though centuries or millennia would pass back home on Earth. This is why special relativity is so important in understanding the feasibility of interstellar travel. It’s not just about how long the trip takes — it’s about how time itself is experienced differently depending on the speed you’re traveling at.

Why This Matters

This simulation demonstrates that interstellar travel may be possible, but it’s not without enormous challenges. Time dilation offers an advantage to the crew on the spacecraft, but the vast distances mean that even at near-light speeds, the journey could take centuries or more from Earth’s perspective.

The interplay of distance, speed, and time reveals just how difficult — but also fascinating — it would be to travel across the cosmos. While the travelers may experience only a few hundred years, their destination could still be over a millennium away from Earth’s perspective. This provides a striking reminder of the immense scales involved when contemplating the possibility of contacting alien civilizations.

Transition to Part 5: The Final Challenge — Have We Ever Encountered Alien Life?

Now that we’ve tackled the vast distances between civilizations, we face our final challenge: Could we have already encountered alien life and not known it? Or more excitingly, what are the odds we will encounter alien life in the future? In Part 5, we’ll dive into these probabilities, exploring past and future encounters, and what they mean for the future of humanity and the search for extraterrestrial intelligence.

Stay tuned for the grand finale of the Drake Equation series!

Next in the series: Are We Alone?: The Real Odds of Encountering Alien Life? (Part 5 of the Drake Equation Series). Or, if you missed the previous part, go back here.

Unless otherwise noted, all images are by the author

Galactic Distances was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.