For early ML Engineers and Data Scientists, to understand memory fundamentals, parallel execution, and how code is written for CPU and GPU.

This article aims to explain the fundamentals of parallel computing. We start with the basics, including understanding shared vs. distributed architectures and communication within these systems. We will explore GPU architecture and how coding elements (using C++ Kokkos) help map architectural principles to code implementation. Finally, we will measure performance metrics (speedup) using the runtime data obtained from running the Kokkos code on both CPU and GPU architectures for vector-matrix multiplication, one of the most common operations in the machine learning domain.
The central theme of the article is exploring and answering questions. It may seem like a lengthy journey, but it will be worth it. Let’s get started!
Fundamentals of System Architecture
I get that parallel computing saves time by running multiple operations at once. But I’ve heard that system time is different from human time or wall-clock time. How is it different?
The smallest unit of time in computing is called a clock tick. It represents the minimum time required to perform an operation, such as fetching data, executing computations, or during communication. A clock tick technically refers to the change of state necessary for an instruction. The state can be processor state, data state, memory state, or control signals. In one clock tick, a complete instruction, part of an instruction, or multiple instructions may be executed.
CPU allows for a limited number of state changes per second. For example, a CPU with 3GHz clock speed allows for 3 billion changes of state per second. There is a limit to the allowable clock speed because each clock tick generates heat, and excessive speed can damage the CPU chip due to the heat generated.
Therefore, we want to utilize the available capacity by using parallel computing methodologies. The purpose is to hide memory latency (the time it takes for the first data to arrive from memory), increase memory bandwidth (the amount of data transferred per unit of time), and enhance compute throughput (the tasks performed in a clock tick).
To compare performance, such as when calculating efficiency of a parallel program, we use wall-clock time instead of clock ticks, since it includes all real-time overheads like memory latency and communication delays, that cannot be directly translated to clock ticks.
What does the architecture of a basic system look like?
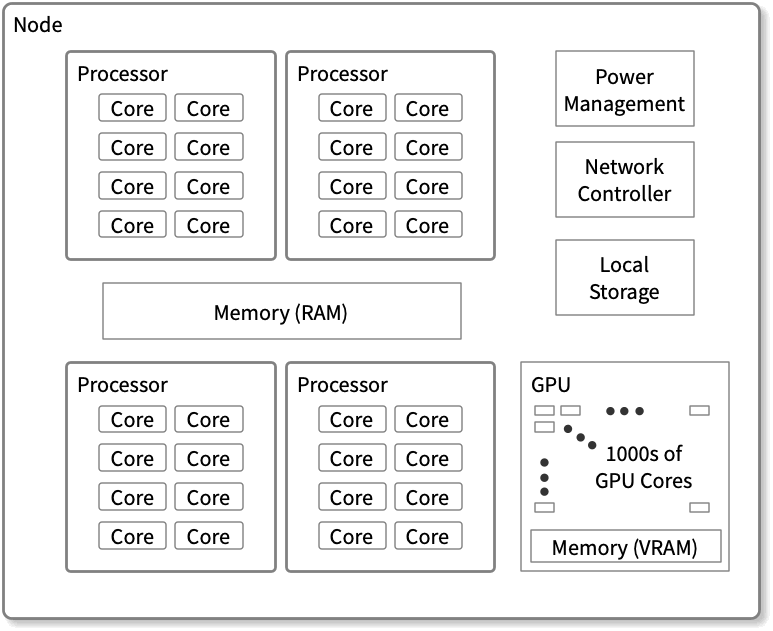
A system can consist of a single processor, a node, or even a cluster. Some of the physical building blocks of a system are —
- Node — A physical computer unit that has several processor chips. Multiple nodes combine to form a cluster.
- Processor Chips — Chips contain multiple processing elements called cores.
- Core — Each core is capable of running an independent thread of execution.
In set terms, a node can have a one-to-many relationship with processor chips, and each processor chip can have a one-to-many relationship with cores. The image below gives a visual description of a node with processors and cores.
The non-physical components of a system include threads and processes —
- Thread — Thread is a sequence of CPU instructions that operating system treats as a single unit for scheduling and execution purposes.
- Process — In computing, a process is a coherent unit of resource allocation, including memory, file handlers, ports and devices. A single process may manage resources for several threads. Threads can be modelled as components of a process.
So, do threads run on cores on the same system, or can they be spread across different systems for a single program? And in either case, how do they communicate? How’s memory handled for these threads ? Do they share it, or do they each get their own separate memory?
A single program can execute across multiple cores on the same or different systems/ nodes. The design of the system and the program determines whether it aligns with the desired execution strategy.
When designing a system, three key aspects must be considered: execution (how threads run), memory access (how memory is allocated to these threads), and communication (how threads communicate, especially when they need to update the same data). It’s important to note that these aspects are mostly interdependent.
Execution
Serial execution — This uses a single thread of execution to work on a single data item at any time.
Parallel execution — In this, more than one thing happens simultaneously. In computing, this can be —
- One worker — A single thread of execution operating on multiple data items simultaneously (vector instructions in a CPU). Imagine a single person sorting a deck of cards by suit. With four suits to categorize, the individual must go through the entire deck to organize the cards for each suit.
- Working Together — Multiple threads of execution in a single process. It is equivalent to multiple people working together to sort a single deck of cards by suit.
- Working Independently — Multiple processes can work on the same problem, utilizing either the same node or multiple nodes. In this scenario, each person would be sorting their deck of cards.
- Any combination of the above.
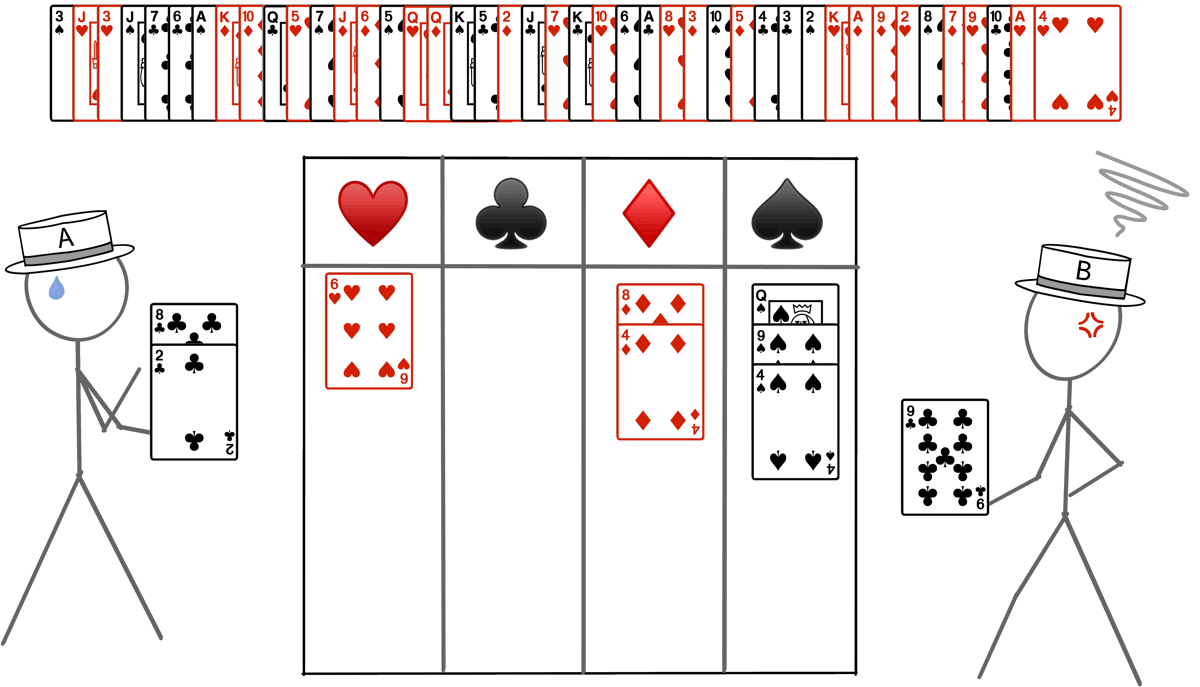
for the clubs suit, so Worker B is temporarily blocked. Ref: Cornell Virtual Workshop
Memory Access
- Shared Memory — When a program runs on multiple cores (a single multithreaded process) on the same system, each thread within the process has access to memory in the same virtual address space.
- Distributed Memory — A distributed memory design is employed when a program utilizes multiple processes (whether on a single node or across different nodes). In this architecture, each process owns a portion of the data, and other processes must send messages to the owner to update their respective parts. Even when multiple processes run on a single node, each has its own virtual memory space. Therefore, such processes should use distributed memory programming for communication.
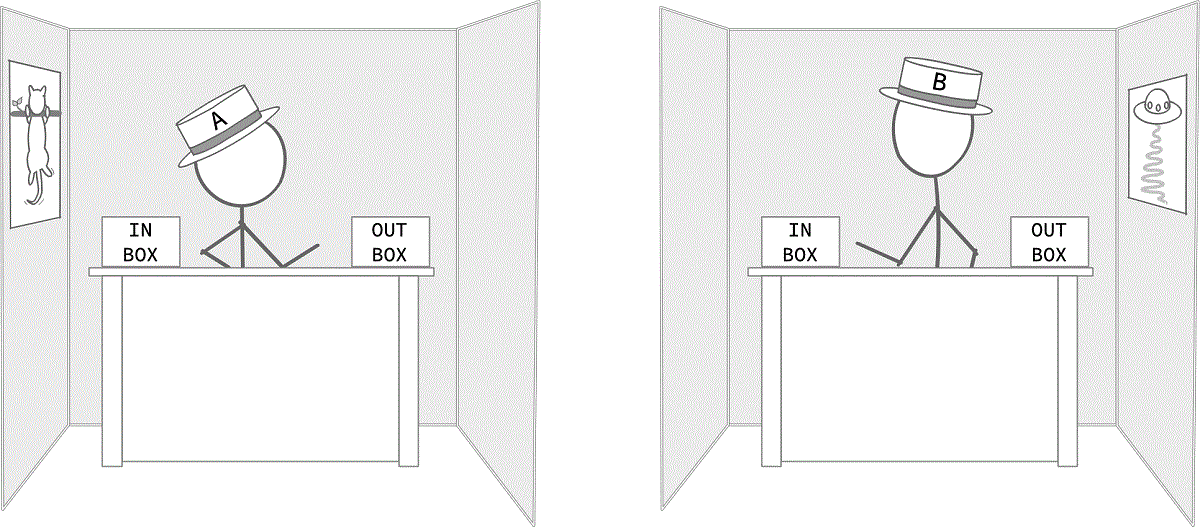
- Hybrid Strategy — Multithreaded processes that can run on the same or different nodes, designed to use multiple cores on a single node through shared memory programming. At the same time, they can employ distributed memory strategies to coordinate with processes on other nodes. Imagine multiple people or threads working in multiple cubicles in the image above. Workers in the same cubicle communicate using shared memory programming, while those in different cubicles interact through distributed memory programming.
Communication
The communication mechanism depends on the memory architecture. In shared memory architectures, application programming interfaces like OpenMP (Open Multi-Processing) enable communication between threads that share memory and data. On the other hand, MPI (Message Passing Interface) can be used for communication between processes running on the same or different nodes in distributed memory architectures.
Parallelization Strategy and Performance
How can we tell if our parallelization strategy is working effectively?
There are several methods, but here, we discuss efficiency and speedup. In parallel computing, efficiency refers to the proportion of available resources that are actively utilized during a computation. It is determined by comparing the actual resource utilization against the peak performance, i.e., optimal resource utilization.
Actual processor utilization refers to the number of floating point operations (FLOP) performed over a specific period.
Peak performance assumes that each processor core executes the maximum possible FLOPs during every clock cycle.
Efficiency for parallel code is the ratio of actual floating-point operations per second (FLOPS) to the peak possible performance.
Speedup is used to assess efficiency and is measured as:
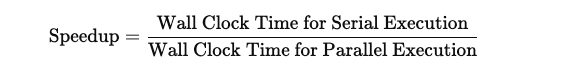
Speedup cannot be greater than the number of parallel resources when programs are limited by computing speed of the processors.
Using speedup, parallel efficiency is measured as :
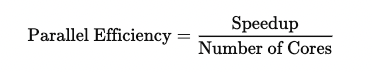
Suppose the serial execution of code took 300 seconds. After parallelizing the tasks using 50 cores, the overall wall-clock time for parallel execution was 6 seconds. In this case, the speedup can be calculated as the wall-clock time for serial execution divided by the wall-clock time for parallel execution, resulting in a speedup of 300s/6s = 50. We get parallel efficiency by dividing the speedup by the number of cores, 50/50 = 1. This is an example of the best-case scenario: the workload is perfectly parallelized, and all cores are utilized efficiently.
Will adding more computing units constantly improve performance if the data size or number of tasks increases?
Only sometimes. In parallel computing, we have two types of scaling based on the problem size or the number of parallel tasks.
Strong Scaling — Increasing the number of parallel tasks while keeping the problem size constant. However, even as we increase the number of computational units (cores, processors, or nodes) to process more tasks in parallel, there is an overhead associated with communication between these units or the host program, such as the time spent sending and receiving data.
Ideally, the execution time decreases as the number of parallel tasks increases. However, if the code doesn’t get faster with strong scaling, it could indicate that we’re using too many tasks for the amount of work being done.
Weak Scaling — In this, problem size increases as the number of tasks increase, so computation per task remains constant. If your program has good weak scaling performance, you can run a problem twice as large on twice as many nodes in the same wall-clock time.
There are restrictions around what we can parallelize since some operations can’t be parallelized. Is that right?
Yes, parallelizing certain sequential operations can be quite challenging. Parallelizing depends on multiple instruction streams and/or multiple data streams.
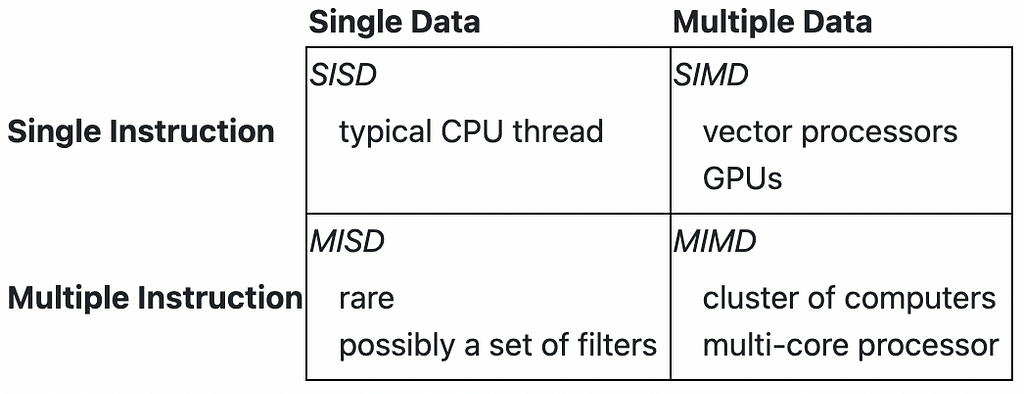
To understand what can be parallelized, let’s look at SIMD in CPUs, which is achieved using vectorization.
Vectorization is a programming technique in which operations are applied to entire arrays at once rather than processing individual elements one by one. It is achieved using the vector unit in processors, which includes vector registers and vector instructions.
Consider a scenario where we iterate over an array and perform multiple operations on a single element within a for loop. When the data is independent, writing vectorizable code becomes straightforward; see the example below:
do i, n
a(i) = b(i) + c(i)
d(i) = e(i) + f(i)
end do
In this loop, each iteration is independent — meaning a(i) is processed independently of a(i+1) and so on. Therefore, this code is vectorizable, that will allow multiple elements of array a to be computed in parallel using elements from b and c, as demonstrated below:
b: | b(i) | b(i+1) | b(i+2) | b(i+3) | ... |
c: | c(i) | c(i+1) | c(i+2) | c(i+3) | ... |
------------------------------------------------
Vectorized Addition (SIMD)
Vector Register 1 (loaded with b values):
| b(i) | b(i+1) | b(i+2) | b(i+3) | ... |
Vector Register 2 (loaded with c values):
| c(i) | c(i+1) | c(i+2) | c(i+3) | ... |
------------------------------------------------
Result in Vector Register 3:
| a(i) | a(i+1) | a(i+2) | a(i+3) | ... |
Modern compilers are generally capable of analyzing such loops and transforming them into sequences of vector operations. Problem arises when an operation in one iteration depends upon the result of a previous iteration. In this case, automatic vectorization might lead to incorrect results. This situation is known as a data dependency.
Data dependencies commonly encountered in scientific code are –
Read After Write (RAW) — Not Vectorizable
do i, n
a(i) = a(i-1) +b(i)
Write After Read (WAR) — Vectorizable
do i, n
a(i) = a(i+1) +b(i)
Write After Write (WAW) — Not Vectorizable
do i, n
a(i%2) = a(i+1) +b(i)
Read After Read (RAR) — Vectorizable
do i, n
a(i) = b(i%2) + c(i)
Adhering to certain standard rules for vectorization — such as ensuring independent assignments in loop iterations, avoiding random data access, and preventing dependencies between iterations — can help write vectorizable code.
GPU architecture and cross-architectural code
When data increases, it makes sense to parallelize as many parallelizable operations as possible to create scalable solutions, but that means we need bigger systems with lots of cores. Is that why we use GPUs? How are they different from CPUs, and what leads to their high throughput?
YES!
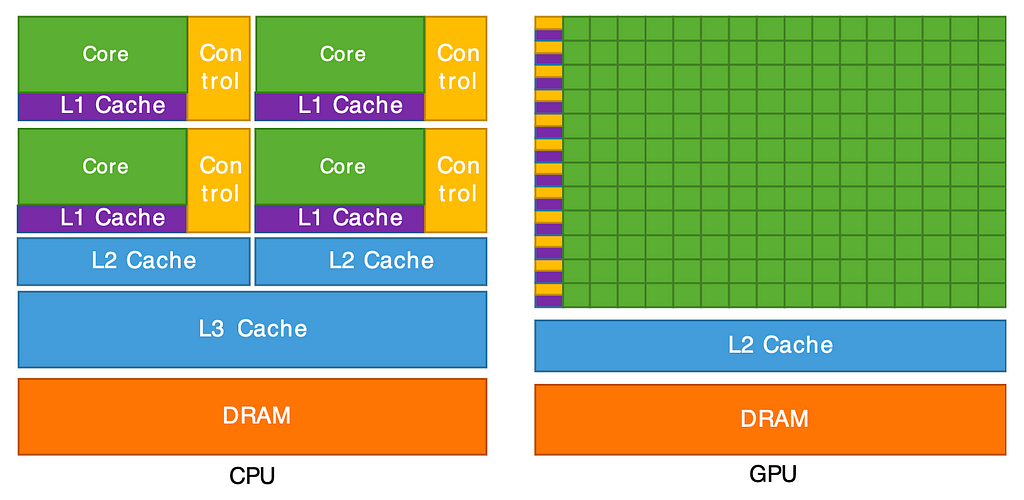
GPUs (Graphics processing units) have many more processor units (green) and higher aggregate memory bandwidth (the amount of data transferred per unit of time) as compared to CPUs, which, on the other hand, have more sophisticated instruction processing and faster clock speed. As seen above, CPUs have more cache memory than GPUs. However, CPUs have fewer arithmetic logic units (ALUs) and floating point units (FPUs) than GPUs. Considering these points, using CPUs for complex workflow and GPUs for computationally intensive tasks is intuitive.
GPUs are designed to produce high computational throughput using their massively parallel architecture. Their computational potential can be measured in billions of floating point operations per second (GFLOPS). GPU hardware comes in the form of standard graphic cards (NVIDIA quad), High-end accelerator cards (NVIDIA Tesla), etc.
Two key properties of the graphics pipeline that enable parallelization and, thus, high throughput are —
- Independence of Objects — A typical graphics scene consists of many independent objects; each object can be processed separately without dependencies on the others.
- Uniform Processing Steps — The sequence of processing steps is the same for all objects.
So, multiple cores of GPUs work on different data at the same time, executing computations in parallel like a SIMD (Single Instruction Multiple Data) architecture. How are tasks divided between cores? Does each core run a single thread like in the CPU?
In a GPU, Streaming Multiprocessors (SMs) are similar to cores in a CPU. Cores in GPUs are similar to vector lanes in CPUs. SMs are the hardware units that house cores.
When a function or computation, referred as a kernel, is executed on the GPU, it is often broken down into thread blocks. These thread blocks contain multiple threads; each SM can manage many threads across its cores. If there are more thread blocks than SMs, multiple thread blocks can be assigned to a single SM. Also, multiple threads can run on a single core.
Each SM further divides the thread blocks into groups called warps, with each warp consisting of 32 threads. These threads execute the same stream of instructions on different data elements, following a Single Instruction, Multiple Data (SIMD) model. The warp size is set to 32 because, in NVIDIA’s architecture, CUDA cores are grouped into sets of 32. This enables all threads in a warp to be processed together in parallel by the 32 CUDA cores, achieving high efficiency and optimized resource utilization.
In SIMD (Single Instruction, Multiple Data), a single instruction acts uniformly on all data elements, with each data element processed in exactly the same way. SIMT (Single Instruction, Multiple Threads), which is commonly used in GPUs, relaxes this restriction. In SIMT, threads can be activated or deactivated so that instruction and data are processed in active threads; however, the local data remains unchanged on inactive threads.
I want to understand how we can code to use different architectures. Can similar code work for both CPU and GPU architectures? What parameters and methods can we use to ensure that the code efficiently utilizes the underlying hardware architecture, whether it’s CPUs or GPUs?
Code is generally written in high-level languages like C or C++ and must be converted into binary code by a compiler since machines cannot directly process high-level instructions. While both GPUs and CPUs can execute the same kernel, as we will see in the example code, we need to use directives or parameters to run the code on a specific architecture to compile and generate an instruction set for that architecture. This approach allows us to use architecture-specific capabilities. To ensure compatibility, we can specify the appropriate flags for the compiler to produce binary code optimized for the desired architecture, whether it is a CPU or a GPU.
Various coding frameworks, such as SYCL, CUDA, and Kokkos, are used to write kernels or functions for different architectures. In this article, we will use examples from Kokkos.
A bit about Kokkos — An open-source C++ programming model for performance portability for writing Kernels: it is implemented as a template library on top of CUDA, OpenMP, and other backends and aims to be descriptive, in the sense that we define what we want to do rather than prescriptive (how we want to do it). Kokkos Core provides a programming model for parallel algorithms that uses many-core chips and shares memory across those cores.
A kernel has three components —
- Pattern — Structure of the computation: for, scan, reduction, task-graph
- Execution policy — How computations are executed: static scheduling, dynamic scheduling, thread teams.
- Computational Body — Code which performs each unit of work. e.g., loop body
Pattern and policy drive computational body. In the example below, used just for illustration, ‘for’ is the pattern, the condition to control the pattern (element=0; element<n; ++element) is the policy, and the computational body is the code executed within the pattern
for (element=0; element<n; ++element){
total = 0;
for(qp = 0; qp < numQPs; ++qp){
total += dot(left[element][qp], right[element][qp]);
}
elementValues[element] = total;
}
The Kokkos framework allows developers to define parameters and methods based on three key factors: where the code will run (Execution Space), what memory resources will be utilized (Memory Space), and how data will be structured and managed (Data Structure and Data management).
We primarily discuss how to write the Kokkos kernel for the vector-matrix product to understand how these factors are implemented for different architectures.
But before that, let’s discuss the building blocks of the kernel we want to write.
Memory Space —
Kokkos provides a range of memory space options that enable users to control memory management and data placement on different computing platforms. Some commonly used memory spaces are —
- HostSpace — This memory space represents the CPU’s main memory. It is used for computations on the CPU and is typically the default memory space when working on a CPU-based system.
- CudaSpace — CudaSpace is used for NVIDIA GPUs with CUDA. It provides memory allocation and management for GPU devices, allowing for efficient data transfer and computation.
- CudaUVMSpac — For Unified Virtual Memory (UVM) systems, such as those on some NVIDIA GPUs, CudaUVMSpace enables the allocation of memory accessible from both the CPU and GPU without explicit data transfers. Cuda runtime automatically handles data movement at a performance hit.
It is also essential to discuss memory layout, which refers to the organization and arrangement of data in memory. Kokkos provides several memory layout options to help users optimize their data storage for various computations. Some commonly used memory layouts are —
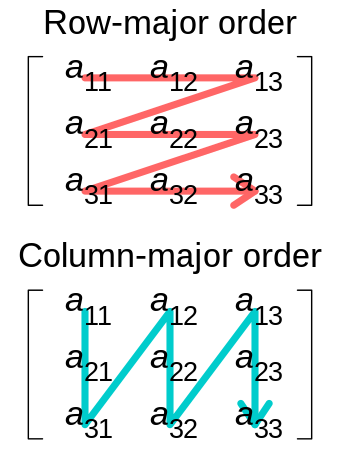
- LayoutRight (also known as Row-Major) is the default memory layout for multi-dimensional arrays in C and C++. In LayoutRight, the rightmost index varies most rapidly in memory. If no layout is chosen, the default layout for HostSpace is LayoutRight.
- LayoutLeft (also known as Column-Major) — In LayoutLeft, the leftmost index varies most rapidly in memory. If no layout is chosen, the default layout for CudaSpace is LayoutLeft.
In the programmatic implementation below, we defined memory space and layout as macros based on the compiler flag ENABLE_CUDA, which will be True if we want to run our code on GPU and False for CPU.
// ENABLE_CUDA is a compile time argument with default value true
#define ENABLE_CUDA true
// If CUDA is enabled, run the kernel on the CUDA (GPU) architecture
#if defined(ENABLE_CUDA) && ENABLE_CUDA
#define MemSpace Kokkos::CudaSpace
#define Layout Kokkos::LayoutLeft
#else
// Define default values or behavior when ENABLE_CUDA is not set or is false
#define MemSpace Kokkos::HostSpace
#define Layout Kokkos::LayoutRight
#endif
Data Structure and Data Management —
Kokkos Views — In Kokkos, a “view” is a fundamental data structure representing one-dimensional and multi-dimensional arrays, which can be used to store and access data efficiently. Kokkos views provide a high-level abstraction for managing data and is designed to work seamlessly with different execution spaces and memory layouts.
// View for a 2d array of data type double
Kokkos::View<double**> myView("myView", numRows, numCols);
// Access Views
myView(i, j) = 42.0;
double value = myView(i, j);
Kokkos Mirroring technique for data management — Mirrors are views of equivalent arrays residing in possible different memory spaces, which is when we need data in both CPU and GPU architecture. This technique is helpful for scenarios like reading data from a file on the CPU and subsequently processing it on the GPU. Kokkos’ mirroring creates a mirrored view of the data, allowing seamless sharing between the CPU and GPU execution spaces and facilitating data transfer and synchronization.
To create a mirrored copy of the primary data, we can use Kokkos’ create_mirror_view() function. This function generates a mirror view in a specified execution space (e.g., GPU) with the same data type and dimensions as the primary view.
// Intended Computation -
// <y, A*x> = y^T * A * x
// Here:
// y and x are vectors.
// A is a matrix.
// Allocate y, x vectors and Matrix A on device
typedef Kokkos::View<double*, Layout, MemSpace> ViewVectorType;
typedef Kokkos::View<double**, Layout, MemSpace> ViewMatrixType;
// N and M are number of rows and columns
ViewVectorType y( "y", N );
ViewVectorType x( "x", M );
ViewMatrixType A( "A", N, M );
// Create host mirrors of device views
ViewVectorType::HostMirror h_y = Kokkos::create_mirror_view( y );
ViewVectorType::HostMirror h_x = Kokkos::create_mirror_view( x );
ViewMatrixType::HostMirror h_A = Kokkos::create_mirror_view( A );
// Initialize y vector on host.
for ( int i = 0; i < N; ++i ) {
h_y( i ) = 1;
}
// Initialize x vector on host.
for ( int i = 0; i < M; ++i ) {
h_x( i ) = 1;
}
// Initialize A matrix on host.
for ( int j = 0; j < N; ++j ) {
for ( int i = 0; i < M; ++i ) {
h_A( j, i ) = 1;
}
}
// Deep copy host views to device views.
Kokkos::deep_copy( y, h_y );
Kokkos::deep_copy( x, h_x );
Kokkos::deep_copy( A, h_A );
Execution Space —
In Kokkos, the execution space refers to the specific computing environment or hardware platform where parallel operations and computations are executed. Kokkos abstracts the execution space, enabling code to be written in a descriptive manner while adapting to various hardware platforms.
We discuss two primary execution spaces —
- Serial: The Serial execution space is a primary and portable option suitable for single-threaded CPU execution. It is often used for debugging, testing, and as a baseline for performance comparisons.
- Cuda: The Cuda execution space is used for NVIDIA GPUs and relies on CUDA technology for parallel processing. It enables efficient GPU acceleration and management of GPU memory.
Either the ExecSpace can be defined, or it can be determined dynamically based on the Memory space as below:
// Execution space determined based on MemorySpace
using ExecSpace = MemSpace::execution_space;
How can we use these building blocks to write an actual kernel? Can we use it to compare performance between different architectures?
For the purpose of writing a kernel and performance comparison, we use following computation:
<y, A*x> = y^T * (A * x)
Here:
y and x are vectors.
A is a matrix.
<y, A*x> represents the inner product or dot product of vectors y
and the result of the matrix-vector multiplication A*x.
y^T denotes the transpose of vector y.
* denotes matrix-vector multiplication.
The kernel for this operation in Kokkos —
// Use a RangePolicy.
typedef Kokkos::RangePolicy<ExecSpace> range_policy;
// The below code is run for multiple iterations across different
// architectures for time comparison
Kokkos::parallel_reduce( "yAx", range_policy( 0, N ),
KOKKOS_LAMBDA ( int j, double &update ) {
double temp2 = 0;
for ( int i = 0; i < M; ++i ) {
temp2 += A( j, i ) * x( i );
}
update += y( j ) * temp2;
}, result );
For the above kernel, parallel_reduce serves as the pattern, range_policy defines the policy, and the actual operations constitute the computational body.
I executed this kernel on a TACC Frontera node which has an NVIDIA Quadro RTX 5000 GPU. The experiments were performed with varying values of N, which refers to the lengths of the vectors y and x, and the number of rows in matrix A. Computation was performed 100 times to get notable results, and the execution time of the kernel was recorded for both Serial (Host) and CUDA execution spaces. I used ENABLE_CUDA compiler flag to switch between execution environments: True for GPU/CUDA execution space and False for CPU/serial execution space. The results of these experiments are presented below, with the corresponding speedup.
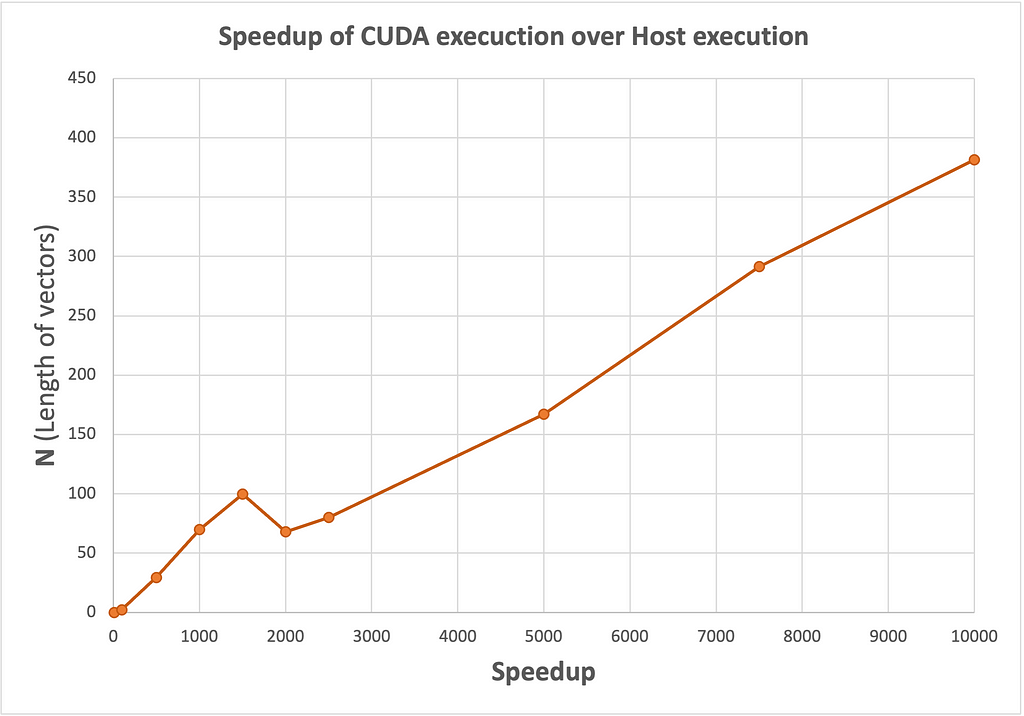
We notice that the speedup increases significantly with the size of N, indicating that the CUDA implementation becomes increasingly advantageous for larger problem sizes.
That’s all for now! I hope this article has been helpful in getting started on the right foot in exploring the domain of computing. Understanding the basics of the GPU architecture is crucial, and this article introduces one way of writing cross-architectural code that I experimented with. However, there are several methods and technologies worth exploring.
While I’m not a field expert, this article reflects my learning journey from my brief experience working at TACC in Austin, TX. I welcome feedback and discussions, and I would be happy to assist if you have any questions or want to learn more. Please refer to the excellent resources below for further learning. Happy computing!
I want to acknowledge that this article draws from three primary sources. The first is the graduate-level course SDS394: Scientific and Technical Computing at UT Austin, which provided essential background knowledge on single-core multithreaded systems. The second is the Cornell Virtual Workshop: Parallel Programming Concepts and High Performance Computing (https://cvw.cac.cornell.edu/parallel), which is a great resource to learn about parallel computing. The Kokkos code implementation is primarily based on available at https://github.com/kokkos/kokkos-tutorials. These are all amazing resources for anyone interested in learning more about parallel computing.
References/Resources:
- GitHub – VictorEijkhout/TheArtofHPC_pdfs: All pdfs of Victor Eijkhout’s Art of HPC books and courses
- Frontera – TACC HPC Documentation
- Cornell Virtual Workshop: Parallel Programming Concepts and High Performance Computing
- Cornell Virtual Workshop: Understanding GPU Architecture
- Cornell Virtual Workshop: Vectorization
- GitHub – kokkos/kokkos-tutorials: Tutorials for the Kokkos C++ Performance Portability Programming Ecosystem
- Kokkos Lecture Series
From Parallel Computing Principles to Programming for CPU and GPU Architectures was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
From Parallel Computing Principles to Programming for CPU and GPU Architectures