
Design, modelling, and simulation of real-world AI systems to improve performance on object detection tasks using finite state machines.

Background
Problem understanding
Recently, I came across one of the great cases of using Raspberry Pi and Python for creating a computer vision-based system for object detection. In short, one guy created a device that keeps the neighbor’s chickens away from his property. After following the Reddit thread, it became apparent that the problem is quite pervasive and not limited to certain bird species, if at all. The top rated comments include:
“I need one of these for the ducks my neighbor feeds and then they sh*t all over my lawn.” — Light_Beard
“I need this for cats in my yard at night.” — Buddha_
“Does it work on kids on Halloween? Asking for a friend.” — HardPawns
Well, one might argue that the problem is not that important and quite legitimately suggest simply asking the neighbors to sort out those hens. However, this is clearly not an engineer’s way to tackle this. Suppose you had already built an AI-assisted bird detection system equipped with a water blaster to chase unwelcome hens away from the yard. The caveat is that its operating version does not perform as well as expected, resulting in still noticeable water usage for sprinkling and lawn cleanup. Hence, chickens run and water bills remain lofty. How to address the challenge?
Model-based engineering for complex systems
Here, we are about to tackle this real-world problem by designing a computational model to simulate the complete chicken-on-the-lawn cycle and later optimize its parameters so that we can reduce water consumption. To do so, we will employ different techniques, including those from automata theory and randomized algorithms.
In particular, this article focuses on modelling and simulation aspects so that you learn how to describe behavior of a real system and design a finite state machine reflecting its dynamics. Then, you will explore the path of implementing such systems in Python and discover ways to leverage computer vision-based models by optimizing its performance on object detection. This should be fun!
Disclaimer: This work is a part of the “Bird by Bird using Deep Learning” series and is devoted to modelling and simulation of real-life systems for computer vision applications using finite automata. All actors, states, events and outputs are the products of the FSM design process for educational purposes only. Any resemblance to actual persons, birds, or real events is purely coincidental.
Introducing the related work
Finite state machines for modelling and simulation
Finite-state machine (FSM) or finite automaton is a mathematical model that can be used to represent and analyse dynamic behavior of a system by describing it through discrete states, transitions between those states, and a set of rules triggering these transitions.
The history of FSM traces back to the mid-20th century, marked by pivotal milestones in automata theory and the theory of computation. Early contributions by luminaries such as Alan Turing and John von Neumann laid the foundation, but it was in the 1950s and 1960s that FSM took a significant leap forward. Notably, Edward F. Moore and George H. Mealy independently introduced two primary types of FSMs, Moore and Mealy machines, respectively.
These FSM types differ in their approach: Moore machines determine next states based solely on the current state, while the Mealy ones associate outputs with the current state and input, offering enhanced adaptability. Originally used in digital circuits, FSMs, in particular Mealy machines, with their responsiveness to external input signals, have become widespread in the design of complex systems that accompany our daily lives.
FSMs are found in both hardware and software applications. Look around — almost all electronic and computing devices have some sort of finite automata — from vending machines to CPUs, from basic electronic devices to programmable logical controllers for smart home automation. They are also taken in software and game development and, of course, can be used to create adaptive AI-assisted systems for real-time object detection.
Discrete math strikes back
At its core, a deterministic finite automaton includes states, inputs, and a transition function. States represent distinct conditions of the system, while inputs trigger switches between states. The transition function defines rules of how the machine transitions between states. Mathematically, such state machine can be represented using a 5-tuple, denoted as M=(Q, Σ, δ, q₀, F), where:
- Q is a set of states representing distinct configurations of the system.
- Σ is a set of inputs consisting of events that trigger state changes.
- Transition function δ governs how the system switches between states given an input (δ:Q×Σ→Q).
- Initial State q₀ is a starting state of the system to be initialized with, where q₀∈Q.
- F is a subset of Q (F⊆Q) consisting of final states.
This way, for any given state and specific input symbol, there is a unique next state determined by the transition function δ, which is typically represented by a state transition table or diagram, specifying transitions given a combination of the current state and inputs.
FSM design process
The design process of an FSM involves identifying the states (and inputs if applicable), defining the transition function, as well as specifying the initial and final states. The following methodology can be employed for translating complex systems into comprehensible models, aiding in the further analysis, design, and implementation phases. A 5-step FSM design process includes:
- Understanding the problem, analyse the structure of the system.
- Defining key components for a conceptual model to be designed.
- Creating a state diagram or defining a state-transition table.
- Implementing the machine’s states, inputs and outputs, transition logic.
- Testing and experimentally validating the FSM.
This iterative process allows to design a concise representation of the real system’s behavior, allowing for approximations and refinements along the process. For instance, after implementing an FSM (Step 4), you may want to further verify and update the specifications (Steps 2–3), same applies to moving from the experimentation (Step 5) back to the problem definition (Step 1), in order to create a working model that is sufficiently detailed and useful to solve a particular problem.
State machine example
Let us take a simple case of the chicken-on-the-lawn scenario, where a bird can either be present on the lawn or not, as a function of external stimuli initiated by the engineer, who, in turn, can either rest or chase away unwelcome guests trespassing on his property. Thus, the controlling object (the engineer) is intended to compensate for the uncertainty of the independent actors (chickens) parameters. In the given example, the set of final states F includes only one state in which the system terminates, say at the end of the day when there are no chickens around. In this way:
- Q = {q₀, q₁, q₂, ⊙}: Set of states representing No-/Chicken.
- Σ = {α₀, α₁, α₂}: Set of input events — Engineer Rest/Chase, and Sunset.
- F = {⊙} contains the final state representing the end of the day.
Figure 1 provides a state transition diagram consisting of nodes (states) connected by edges (next-state transitions), with the labels above the arcs specifying input events triggering the transitions.
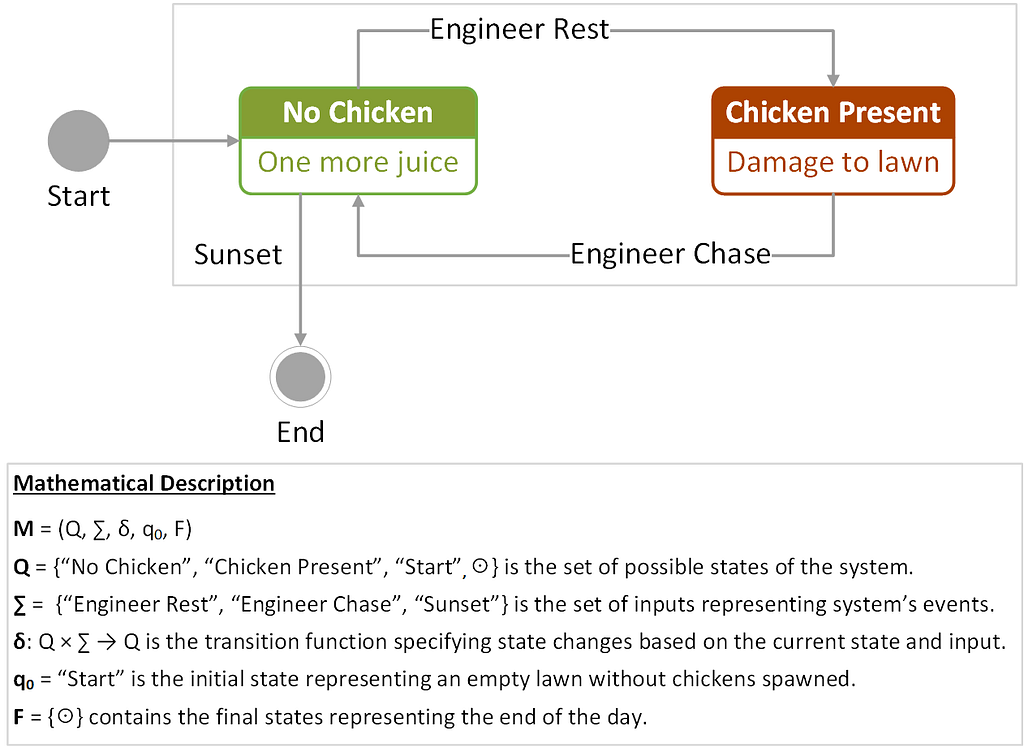
This representation captures the binary nature of the problem, in which a chicken can either be present or not on the lawn. The system responds to the events triggered by the engineer or the sunset. In the diagram, the initial and final states are indicated by circles. The transition function δ for this FSM can also be written in a tabular form, showing state transitions and control actions for the system, as shown in Table 1.
Table 1. State-transition table for the chicken-on-the-lawn FSM example
+========================+========================+========================+
| Current State | Input Event | Next State |
+========================+========================+========================+
| q₀ ≡ ”No Bird” | α₀ ≡ ”Engineer Rest” | q₁ |
+------------------------+------------------------+------------------------+
| q₁ ≡ ”Bird Present” | α₁ ≡ ”Engineer Chase” | q₀ |
+------------------------+------------------------+------------------------+
| q₀ | α₂ ≡ ”Sunset” | ⊙ |
+------------------------+------------------------+------------------------+
Thus, by completing five straightforward steps we designed a simple state machine. Now that everything has been explained, let’s finally create an FSM-based model representing our challenge with birds on the lawn.
On dealing with the birds-on-the-lawn challenge
What they do on the lawn
As you have learnt in the previous section, finite automata can be used to model almost any process. Imagine you have some chickens hopping around in your backyard this afternoon. What are they doing? Just observe. They’re always moving, singing, or interacting. They’re often flying, probing, or eating. On some occasions, they’re displaying, or doing something that draws our attention, like those neighbor’s chickens messing up with the grass, but let’s set those particulars aside for now. Well, eventually, all the birds are s***ing (nothing personal, feathery ones). For the FSM design, we won’t get into the finer details, instead distilling essential components with logic for our simulation. Let the FSM take water adventures to the next level of play!
System description
Concerning the chickens, here, we are going to describe the system to reflect our down-to-earth scenario in order to optimize parameters of the object detection system and reduce water costs for lawn cleaning. For the reference, take another look at the previous FSM example. This simple machine differs from the real-life system in some particular aspects. First, we want to actualize the controlling object to include an AI-based device aimed at detecting and repelling birds, this time by means of a high-pressure water sprinkler gun (so the engineer can “self-loop” into the rest state).
Second, we will need to update and/or extend the set of possible states, events, and transitions reflecting complexity of the updated system’s setup. For the latter, why don’t we consider additional bird categories that can be recognized by a computer vision model (e.g., turkeys) thus being potential independent actors for our FSM. Moreover, assuming that bird size varies across species, an irrigation control system would need a more intense water flow and/or pressure to successfully chase a bulky turkey off the lawn than it would for a chicken. Hereafter, for brevity’s sake, we will refer to the chicken-and-turkey-on-the-lawn problem as the CaT problem.
Conceptual modelling
In order to model scenarios where the object detection system has to monitor, classify, and interact with objects trespassing on the property, we will define states, events, and transitions that represent the different aspects of this situation. Our goal is to capture the various states the object detection system and chickens can be in, as well as the events that trigger state transitions.
For the logic design scenarios, consider that at any given moment a bird can enter the yard, mess up with the lawn (or not), and leave the property either for its own or if it was successfully detected and chased away by the AI-based lawn security system. Now, let’s define some main components of the FSM simulation.
States represent possible conditions reflecting the CaT scenarios:
- For hopping targets: Spawn and Intrusion statuses, Attacking and its result, Leaving the lawn.
- For the AI system: Detection State, Sprinkling State.
- Initial state “Start” relates to the entry point of the simulation.
- Final state “End” denotes the termination point of the simulation.
Transitions govern how the system switches between states based on inputs. For instance, the AI model may overlook a bird and miss the sprinkling process, thus, resulting in a number of consequences for the lawn. Here are some other scenarios and conditions we can anticipate:
- From “Intrusion” to “Target Detected” on the “Detection” event.
- From “Target Detected” to “Bird Leaves” events through the sequence of “Sprinkling” and “Hit” events after an intruded bird has been detected and hit by the water sprinkler successfully.
- From “Bird Present” to “Attack”, in case the system has failed at target detection and prediction steps, while the bird was actually on the lawn. The same event shall take place under the conditions that the bird-intruder was detected, but the shot was missed by the system.
This way, the FSM will dynamically progress from one state to another as the AI system interacts with the chickens hopping around. To make task easier and less error-prone, we create a combined state transition and conditions table:
Table 2. FSM inputs describing the events triggering state changes
+====+==================================+==================+================+
| ID | Input Description | Defence System | Enemy Tactics |
| | | Operation Mode | and Waypoints |
+====+==================================+==================+================+
| X₁ | Bird is present on the lawn | | Hopping |
+----+----------------------------------+ Object detection +----------------+
| X₂ | Bird intrudes the lawn | | Start hopping |
+----+----------------------------------+------------------+----------------+
| X₃ | AI-powered detector spots a bird | Start sprinkling | Hopping (still)|
+----+----------------------------------+------------------+----------------+
| X₄ | Bird is hit successfully¹ | | |
+----+----------------------------------+ - | Intimidation |
| X₅ | Target is susceptible² | | |
+----+----------------------------------+------------------+----------------+
| X₆ | Bird spoiled the lawn | | Hopping merrily|
+----+----------------------------------+ Object detection +----------------+
| X₇ | Bird leaves the lawn | | Retreat |
+----+----------------------------------+------------------+----------------+
| X₈ | Simulation period ends (sunset) | - | - |
+----+----------------------------------+------------------+----------------+
ID - input identifier
¹ - aiming and sprinkling modules operated correctly
² - water flow rate is strong enough to chase the bird away
State transition tables
Now, after identifying states and events, we’ll write a combined state transition table with Boolean expressions for the next states. In table 3, we see how the inputs described in Table 2 steer the transitions between the simulation states.
Table 3. FSM state transition table with next-stage transition logic
+========================+========================+========================+
| Current State | Transition Formula | Next State |
+========================+========================+========================+
| Start | TRUE | Spawn |
+------------------------+------------------------+------------------------+
| | X₁ ∨ X₂ | Intrusion |
| |------------------------+------------------------+
| Spawn | ¬X₁ ∧ ¬X₂ | Empty lawn |
+ |------------------------+------------------------+
| | X₈ | End |
+------------------------+------------------------+------------------------+
| | X₃ | Target detected |
| Intrusion |------------------------+------------------------+
| | ¬X₃ | Not detected |
+------------------------+------------------------+------------------------+
| | X₃ | Target detected |
| Empty lawn |------------------------+------------------------+
| | ¬X₃ | Not detected |
+------------------------+------------------------+------------------------+
| Target detected | TRUE | Sprinkling |
+------------------------+------------------------+------------------------+
| | X₁ | Attacking |
| Not detected |------------------------+------------------------+
| | ¬X₁ | Not attacked |
+------------------------+------------------------+------------------------+
| | ¬X₁ ∨ ¬X₄ ∨ ¬X | Miss |
| Sprinkling |------------------------+------------------------+
| | X₁ ∧ X₄ ∧ X₅ | Hit |
+------------------------+------------------------+------------------------+
| | ¬X₁ | Spawn |
| Miss |------------------------+------------------------+
| | X₁ | Attacking |
+------------------------+------------------------+------------------------+
| Hit | TRUE | Bird leaves |
+------------------------+------------------------+------------------------+
| | ¬X₆ | Not attacked |
| Attacking |------------------------+------------------------+
| | X₆ | Bird attacked |
+------------------------+------------------------+------------------------+
| | ¬X₇ | Spawn |
| Not attacked |------------------------+------------------------+
| | X₇ | Bird leaves |
+------------------------+------------------------+------------------------+
| | ¬X₇ | Spawn |
| Bird attacked |------------------------+------------------------+
| | X₇ | Bird leaves |
+------------------------+------------------------+------------------------+
| Bird leaves | TRUE | Spawn |
+------------------------+------------------------+------------------------+
In most cases, a single input determines the next state. However, we have to consider a number of conditions simultaneously for switching from “Spawn” or “Sprinkling”. You could also notice that for some states, transitions don’t depend on the external information, like for “Start” or “Hit”. These states are either special (as “Start”) or trigger auxiliary actions. The latter don’t have a direct influence on the story we simulate (i.e. in that regard, they can be combined with the subsequent states) but are important for gathering simulation statistics.
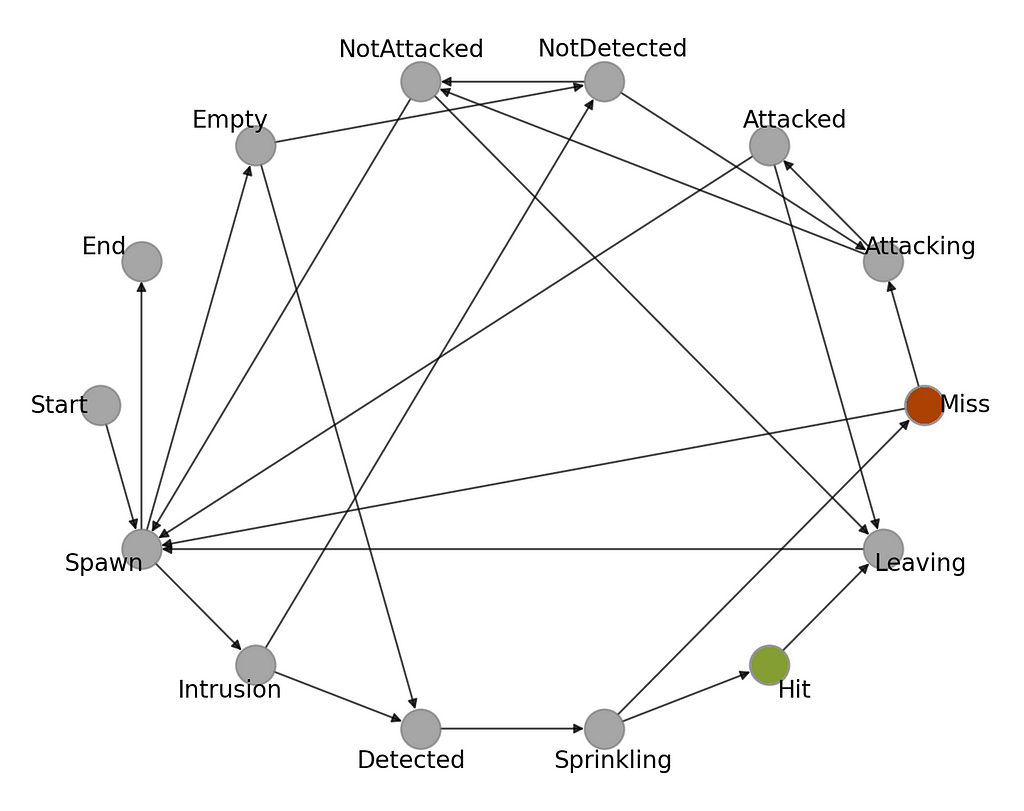
Finally, let’s look at its visual representation. Figure 3 presents the state transition graph corresponding to the CaT system going through during its lifetime. You can probably see the connection already. Moving forward with the following article, you will learn how to implement this FSM in Python and how to use it to optimize parameters of the AI-assisted bird detection system in order to reduce water cost.
Conclusions
In this article, we explored how to apply finite state machines in practice to build a model for addressing the CaT problem, allowing for high-level problem analysis and solution design.
We have described complex yard processes by applying the FSM formalism to individual actors and the interactions between them, thereby creating a holistic view of the internal dynamics of the real-world situation, in which we had to deal with neighborhood birds trespassing on the property.
This allowed us to create a simulation that reflects, among other things, the operation of the AI-assisted security system equipped with a water pressure controller for sprinkling and aimed at object detection and chasing away unwelcome guests spoiling the lawn.
What’s next?
In the upcoming series of articles, we will further investigate the topic of simulation of real-life scenarios using FSMs and its practical applications for addressing a non-analytic optimization problem of water cost reduction.
Specifically, the next article will feature a Python tutorial from which you will learn how to implement an FSM-driven simulation from scratch as well as how to employ it as a part of a stochastic optimization pipeline. Based on the simulation created, we then examine how to leverage it for improving the resource efficiency of our lawn security system by applying Monte-Carlo and eXplainable AI (XAI) techniques to optimize performance of a computer vision-based subsystem for bird detection.
Interested to keep it on? Stay updated on more materials at — https://github.com/slipnitskaya/caltech-birds-advanced-classification and https://medium.com/@slipnitskaya.
References
- Moore, Edward F. “Gedanken-experiments on sequential machines.” Automata studies 34 (1956): 129–153.
- Mealy, George H. “A method for synthesizing sequential circuits.” The Bell System Technical Journal 34.5 (1955): 1045–1079.
- Sipser, M. “Introduction to the Theory of Computation.” 2nd ed., Thomson Course Technology (2006).
Finite Automata Simulation for Leveraging AI-Assisted Systems was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Finite Automata Simulation for Leveraging AI-Assisted Systems
Go Here to Read this Fast! Finite Automata Simulation for Leveraging AI-Assisted Systems
