Estimating Individualized Treatment Rules Using Outcome Weighted Learning

A non-parametric approach for fitting personalized treatments to patients

In many diseases, different patients will react differently to different treatments. A drug that is beneficial for some patients may not work for other patients with different characteristics. Therefore, healthcare can significantly improve by treating patients based on their characteristics, rather than treating all patients with the same treatment.

In this article, I will try to show you how we can train a machine-learning model to learn the optimal personalized treatment.

This article is about the field of personalized health care, but the results can be used in any field. For example: Different people will react differently to different ads on social media, so, in cases where there are multiple ads for the same product, how do you choose which ad to show to which viewers?

This method is useful in any case where you have to give a treatment but you can only give one treatment to every individual in the sample and therefore you have no way of knowing how that individual would respond to the other treatments.

Let’s formalize the problem

An experiment was performed to compare two (or more) treatments. We’ll name them T = 1,2… A vector of covariates X represents every patient. Every patient i with a covariates vector Xᵢ, that was given a treatment Tᵢ has a recorded response to the treatment, Rᵢ.

For example, let’s assume that you want to test 3 different drugs for diabetes, we’ll name these drugs “1”, “2”, “3”.

We have a patient named Esther, she is 64 years old, she’s been diagnosed with diabetes 8 years ago, she weighs 65 kilos and her height is 1.54 meters. Esther has received drug “1” and her blood sugar was reduced by 10 points after being given the new drug.

In our example, the data point we have on Esther is X = {Female, 64 years old, 8 years since diagnosis, 65 kg, 1.54 meters}, T = “1”, R = 10.

In this setting, we would like to learn an optimal decision rule D(x), that assigns a treatment “1”, “2”, or “3” to every patient to optimize the outcome for that patient.

The old way of solving this problem was to model the outcome as a function of the data and the treatment and denote the predicted outcome as f(X,T). Once we have a model we can create a decision rule D(x): we compute f(X,1), f(X,2), and f(X,3) and give the patient the drug that maximizes their expected outcome.

This solution can work when we have a fairly good understanding of the underlying model that created the data. In this case, all we need is some finetuning to find the best parameters for our case.

However, if the model is bad then our results will be bad, regardless of the amount of data at hand.

Can we come up with a decision rule that is not parametric and does not assume any prior knowledge of the relationship between the data and the treatment result?

The answer is yes, we can use machine learning to find a decision rule that does not make any assumptions about the relationship between the response and the treatment!

Solving with a non-parametric approach using Outcome Weighted Learning

The way to solve this problem is to solve a classification problem where the labels are the treatments given in the experiment and every data point i is weighted by Rᵢ/π(Tᵢ|Xᵢ), where π(Tᵢ|Xᵢ) is the propensity of getting treatment Tᵢ, given that you have the characteristics Xᵢ, which can be computed from the data.

This makes sense because we try to follow the experiment’s results, but only where it worked best. The reason we divide by the propensities is to correct the category size bias. If you’ve learned some reinforced learning then this whole process should look familiar to you.

Here is an example of an owl classifier using SVM. You can feel free to use any classifier you like.

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import svm

def owl_classifier(X_train, T, R, kernel, gamma):
  n = len(T)
  pi = np.zeroes(n) #Initialize pi as a vector of zeroes
  probs = LogisticRegression().fit(X_train, T).predict_proba(X_train)#This is a n*unique(T) matrix that gives every person the probability of getting each treatment
  for t in np.unique(T):
    pi += probs[,t]*(T==t) #Every data point is assigned the probability of getting the treatment that it got, given the covariates
  clf = svm.SVC(kernel = kernel, gamma = gamma) # initialize an svm classifier, the parameters need to be found by cross validation
  clf.fit(X_train, T, sample_weight = R/pi) # fit the classifier with the treatments as labels and R/pi as sample weights
    

Simulation to test the OWL method

Simulating data can test the owl method. We create the reward function so that we know what the optimal treatment is for every patient. We can then train the OWL classifier on the data and check how well it fits the optimal classifier.

For example:

I created 50 features that are all sampled from a U([-1,1]) distribution. I gave the patients one of three treatments {1,2,3} at random, uniformly.

The response function is sampled from a N(μ, 1) distribution, where μ = (X₁ + X₂)*I(T=1) + (X₁ — X₂)*I(T=2) + (X₂-X₁)*I(T=3)

# This code block creates the data for the simulation
import numpy as np

n_train = 500 # I purposely chose a small training set to simulate a medical trial
n_col = 50 # This is the number of features
n_test = 1000
X_train = np.random.uniform(low = -1, high = 1, size = (n_train, n_col))
T = np.random.randint(3, size = n_train) # Treatments given at random uniformly
R_mean = (X_train[:,0]+X_train[:,1])*(T==0) + (X_train[:,0]-X_train[:,1])*(T==1) + (X_train[:,1]-X_train[:,0])*(T==2)
R = np.random.normal(loc = R_mean, scale = .1) # The stanadard deviation can be tweaked
X_test = np.random.uniform(low = -1 , high = 1, size = (n_test, n_col))

# The optimal classifier can be deduced from the design of R
optimal_classifier = (1-(X_test[:,0] >0)*(X_test[:,1]>0))*((X_test[:,0] > X_test[:,1]) + 2*(X_test[:,1] > X_test[:,0]))

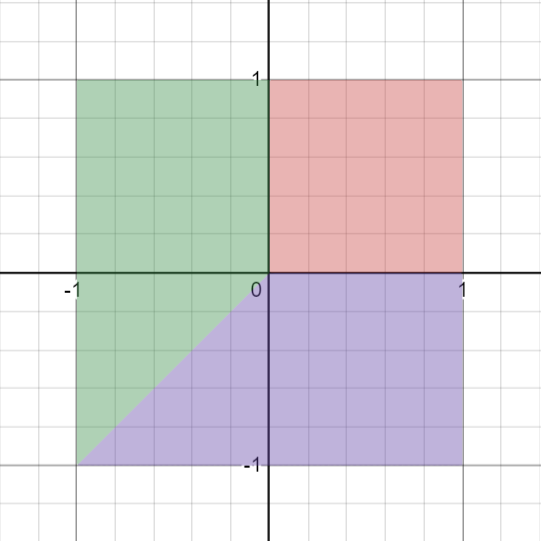
It is not hard to see that the optimal treatment regime is to give treatment 1 if both X₁ and X₂ are positive. If they are both negative, give treatment 2 if X₂<X₁ and give treatment 3 if X₁<X₂. If X₁ is positive and X₂ is negative, give treatment 2. If X₂ is positive and X₁ is negative, give treatment 3.

Or we can show this with an image. These are the different ranges of the optimal treatment, shown for ranges of X₁, X₂:

I sampled 500 data points with 50 features and the reward function that I described above. I fit an OWL classifier with a Gaussian (‘rbf’) kernel and got the following classifications, which I visualized for values of X₁, X₂:

# Code for the plot 
import seaborn as sns

kernel = 'rbf'
gamma = 1/X_train.shape[1] 
# gamma is a hyperparameter that has to be found by cross validation but this is a good place to start
D = owl_classifier(X_train, T, R, kernel, gamma)
prediction = D.predict(X_test)
sns.scatterplot(x = X_test[:,0], y = X_test[:,1], c = prediction )

In case you missed what happened here: The data was composed of 2 features that affected the response and 48 features of noise. The model managed to learn the effect of the two important features without us modeling this relationship in any way!

This is just one simple example, I made the reward function depend on X₁ and X₂ so that it’s easy to understand and visualize but you can feel free to use other examples and try out different classifiers.

Conclusion

Outcome-weighted learning can be used to learn an optimal treatment in cases where we only see one treatment per patient in the training data, without having to model the response as a function of the features and the treatment.

There is some math that I dropped out from this article that justifies this whole process, I did not just make this up from the top of my head.

Future research on this topic should include:

1. Exploitation vs. exploration: Even after we learned a treatment rule, it’s still beneficial to sometimes explore options that are considered not optimal according to our model. The model can be wrong.
2. Sequential treatment: when there is a sequence of treatments, each one of them changes the state of the patient. The solution for the whole sequence should be found via dynamic programming.
3. Design: in this article, I just assumed the treatments were given according to a given rule. Perhaps we can find some design that can improve the learning process.

Estimating Individualized Treatment Rules Using Outcome Weighted Learning was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.