Entity Type Prediction with Relational Graph Convolutional Network (PyTorch)

This post proposes a Python setup for entity type prediction on heterogenous graphs, using the Relational Graph Convolutional Network (R-GCN). The setup uses the RGCNConv module from PyTorch. The code discussed in this post can be found on GitHub. Before we dive into the setup in Python, knowledge graphs and the R-GCN model will be explained.

Knowledge Graphs

A (knowledge) graph is a relational data representation, expressing relations between entities. The Resource Description Framework (RDF) is a common framework to describe and store relational data [1]. A subject (entity), predicate (relation) and object (entity) are the components of the RDF-triple. In a graph, the entities are the nodes, and the predicates are the relational connections between the nodes. In this post, entities and nodes as well as predicates and relations, are used interchangeably. An example of a subject-predicate-object RDF-triple is: Tarantino directed Kill Bill. An entity in the graph can have a type denoted with an rdf:type predicate. Looking at the RDF-triple example, entity types can be assigned as: Tarentino rdf:type director, Kill Bill rdf:type movie.

To create a knowledge graph, commonly, the data is collected or added with the use of manually, semi-automated and automated methods. DBPedia, Wikidata and Yago are examples of constructed knowledge graphs and are impressive considering their size and collection efforts. However, the problem of incompleteness and missing data remains in these graphs. Missing data, regarding graphs, entails missing RDF-triples in the graph [2]. The aim of entity type prediction is to complement an entity with an rdf:type predicate and its label. Entity type prediction for graph nodes, is a transductive learning task, as the training and evaluation data both are encountered by the model. The rdf:type predicates and labels are pruned, while the graph nodes, for which the prediction is made, remain part of the training data [3].

Graphs that contain multiple entity and relation types are called heterogeneous graphs. Significant research has been conducted on modeling heterogeneous graphs for relation type and entity type prediction. On these tasks, a well-performing model is the Relational Graph Convolutional Network (R- GCN)[4]. The R-GCN model contains relation/predicate specific weights. Besides these weights, other trainable parameters are the entity vector representations (or embeddings). The entity embeddings are comparable to word embeddings. If one would visualize word embeddings into vector space, one would find that the words queen and woman lie closer to each other. For man and king holds the same. When visualizing entity embeddings in a vector space, entities are closer to each other if they are more similar.

R-GCN

In this section we discuss how the R-GCN model operates. First, the message passing framework of the Graph Convolution Network (GCN) is discussed. Message passing means propagating node features by exchanging information between adjacent nodes. The R-GCN’s core operation is comparable to the message passing framework of the GCN. Secondly we dive into the message passing of the R-GCN model.

The GCN model learns the vector representations of the entities in the graph. These representations are input for the model and can be updated with backpropagation. The mechanism for GCN relies on a message passing framework, where through the edges messages get passed which update the node representation. The message passing framework can be achieved by matrix multiplications, where the message passing for a single GCN layer in directed graphs is [5]:

Here X is the vector representation matrix, indicating the features for each node. The relation specific weights are denoted by W. σ is a non-linearity and A is a normalized Laplacian adjacency matrix of the graph. The operation of equation 1 is called message passing as the information of neighboring entities is passed to update the representation of each entity. The message passing framework enables backpropagation to update weights (W) and the entity representation (X). Looking at a single node update with GCN, we rewrite Equation 1 as [5]:

The output vector hi is the updated representation for node i. Ni are the representations of incoming edge neighbors. Ni is used to calculate the average of the sum of vector representations of the neighbors of i. The average is multiplied by the current representation xi of the to-be-updated node i and a weight matrix W. Then, a non-linearity σ is applied. hi is the new node representation, constructed from neighboring vector representations and the previous node representation of i.

The R-GCN model extends GCN to learn node representations on heterogeneous graphs [5]. R-GCN accounts for different relations and the directions of edges (incoming and outgoing) for node representation updates. The message passing operation of a single R-GCN layer with multiple relations can be derived from Equation 1 as [5]:

Here, the adjacency matrix Ar describes the edge connections between the nodes. For each relation r∈R in the graph there exists a relation specific weight matrix Wr. The update for a single entity vi is derived from the massage passing framework of the R-GCN layer (Equation 3) as [4]:

Ni is the set of neighboring nodes connected via incoming and outgoing edges. Wr is the relation specific weight and hj is a neighboring node. The sum of each neighboring vector representation multiplied by the relation specific weight of the connected edge, is taken into account for the node update. Furthermore, W0 is a special weight added to each node that functions as a self-loop. Node i is updated by taking the neighboring node representations into account as well as the current representation of i itself. Therefore, stacking two R-GCN layers, the node representation at layer l is taken into account for updating the same node at layer l+1. ci,r is a regularization term which can be modified according to the desired implementation [4].

Python Setup

In this chapter a python setup is discussed. The entire code, including the setup and run commands can be found on GitHub.

Graph triple storage

Let’s first dive into the data structure of a graph and its triple stores. A common file type to store graph data is the ‘N-triple’ format with the file extension ‘.nt’. Figure 1 displays an example graph file (example.nt) and Figure 2 is the visualization of the graph data.

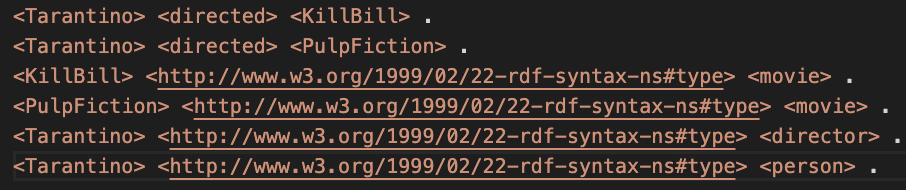
For the sake of clarity in the visualization of example.nt, it was decided to indicate the rdf:type relation with a dotten line. In Figure 2 we see that Tarantino has two type labels and Kill Bill and Pulp Fiction have only one. We will see that this is important to decide for an activation and loss function later on.

Storing nodes, relations and node labels

To create and store important graph information we created the Graph class in graph.py.

import torch

from collections import defaultdict
from torch import Tensor

class Graph:

    RDF_TYPE = '<http://www.w3.org/1999/02/22-rdf-syntax-ns#type>'

    def __init__(self) -> None:
        self.graph_triples: list = None
        self.node_types: dict = defaultdict(set)
        self.enum_nodes: dict = None
        self.enum_relations: dict = None
        self.enum_classes: list = None
        self.edge_index: Tensor = None
        self.edge_type: Tensor = None

The rdf:type relation is hard coded to later remove it from the relation set. Furthermore, variables are created to store important graph information. To use the graph data, we need to parse the ‘.nt’ file and store its contents. There are libraries, like ‘RDFLib’ that can help with this and offer other graph functionalities. However, I found that ‘RDFLib’ does not scale well with larger graphs. Therefore, new code was created to parse the file. To read and store the RDF-triples from a ‘.nt’ file, the function below in the Graph class was created.

def get_graph_triples(self, file_path: str) -> None:
     with open(file_path, 'r') as file:
          self.graph_triples = file.read().splitlines()

The above function stores a list of strings in self.graph_triples: [ ‘<entity> <predicate> <entity> .’,…,‘<entity> <predicate> <entity> .’]. The next step is to store all distinct graph nodes and predicates and to store the node labels.

def init_graph(self, file_path: str) -> None:
    '''intialize graph object by creating and storing important graph variables'''
    
    # give the command to store the graph triples
    self.get_graph_triples(file_path)
    
    # variables to store all entities and predicates
    subjects = set()
    predicates = set()
    objects = set()
    
    # object that can later be printed to get insignt in class (im)balance
    class_count = defaultdict(int)

    # loop over each graph triple and split 2 times on space:' '
    for triple in self.graph_triples:
        triple_list = triple[:-2].split(' ', maxsplit=2)

        # skip triple if there is a blank lines in .nt files
        if triple_list != ['']:
            s, p, o = triple_list[0].lower(), triple_list[1].lower(), triple_list[2].lower()

            # add nodes and predicates
            subjects.add(s)
            predicates.add(p)
            objects.add(o)

             # check if subject is a valid entity and check if predicate is rdf:type
            if str(s).split('#')[0] != 'http://swrc.ontoware.org/ontology' 
                and str(p) == self.RDF_TYPE.lower():
                    class_count[str(o)] += 1
                    self.node_types[s].add(o)

    # create a list with all nodes and then enumerate the nodes
    nodes = list(subjects.union(objects))
    self.enum_nodes = {node: i for i, node in enumerate(sorted(nodes))}

    # remove the rdf:type relations since we would like to predict the types
    # and enumerate the relations and save as dict
    predicates.remove(self.RDF_TYPE)
    self.enum_relations = {rel: i for i, rel in enumerate(sorted(predicates))}

    # enumereate classes
    self.enum_classes = {lab: i for i, lab in enumerate(class_count.keys())}

    # if you want to: print class occurence dict to get insight in class (im)balance
    # print(class_count)

In self.node_types the label(s) for each node are stored. The value for each node is the set of labels. Later this dictionary is used to vectorize node labels. Now, let’s look at the loop over self.graph_triples. We create a triple_list with triple[:-2].split(‘ ‘, maxsplit=2). In triple_list we now have: [‘<entity>’, ‘<predicate>’, ‘<entity>’]. The subject, predicate and object are stored in the designated subjects, predicates and objects sets. Then, if the subject was a valid entity with an rdf:type predicate and type label, the node and its label are added with self.node_types[s].add(o).

From the subjects, predicates and objects sets, the dictionaries self.enum_nodes and self.enum_relations are created, which store nodes and predicates as keys respectively. In these dictionaries the keys are enumerated with integers and stored as the value for each key. The rdf:type relation is removed from the predicates set before storing the numbered relations in self.enum_relations. This is done because we do not want our model to train for the rdf:type relation. Otherwise, through the rdf:type relation the node embedding will be influence and taken into account for each node update. This is prohibited as it would result in information leakage for the prediction task.

Creating edge_index and edge_type

With the stored graph nodes and relations we can create the edge_index and edge_type tensors. The edge_index is a tensor that indicates which nodes are connected. The edge_type tensor stores by which relation the nodes are connected. Importantly to note, to allow the model to pass messages in two directions, the edge_index and edge_type also include the inverse of each edge [4][5]. This enables to update each node representation by incoming and outgoing edges. The code to create the edge_index and edge_type is displayed below.

def create_edge_data(self):
    '''create edge_index and edge_type'''

    edge_list: list = []

    for triple in self.graph_triples:
        triple_list = triple[:-2].split(" ", maxsplit=2)
        if triple_list != ['']:
            s, p, o = triple_list[0].lower(), triple_list[1].lower(), triple_list[2].lower()
            
            # if p is RDF_TYPE, it is not stored
            if self.enum_relations.get(p) != None:
    
                # create edge list and also add inverse edge of each edge
                src, dst, rel = self.enum_nodes[s], self.enum_nodes[o], self.enum_relations[p]
                edge_list.append([src, dst, 2 * rel])
                edge_list.append([dst, src, 2 * rel + 1])
    
    edges = torch.tensor(edge_list, dtype=torch.long).t() # shape(3, (2*number_of_edges - #RDFtype_edges))
    self.edge_index = edges[:2] 
    self.edge_type = edges[2]

In the code above, we start with looping over the graph triples like before. Then we check if the predicate p can be found. If not, the predicate is the rdf:type predicate and this predicate is not stored. Therefore, the triple is not included in the edge data. If the predicate is stored in self.enum_relations the corresponding integers for the subject, predicate and object are assigned to src, dst and rel respectively. The edges and inverse edges are added to edge_list . Distinctive integers for each non-inverse relation are created with 2*rel. For the inverse edge the distinctive integer for the inverse relation is created with 2*rel+1 .

Create training data

Below the class TrainingData of trainingdata.py is displayed. This class creates and stores training, validation and test data for the entity type prediction task.

import torch

from dataclasses import dataclass
from sklearn.model_selection import train_test_split

from graph import Graph

@dataclass
class TrainingData:
    '''class to create and store training data'''
    x_train = None
    y_train = None
    x_val = None
    y_val = None
    x_test = None
    y_test = None

    def create_training_data(self, graph: Graph) -> None:
        train_indices: list = []
        train_labels:list = []

        for node, types in graph.node_types.items():
            # create list with zeros
            labels = [0 for _ in range(len(graph.enum_classes.keys()))]
            for t in types:
                # Assing 1.0 to correct index with class number
                labels[graph.enum_classes[t]] = 1.0
            train_indices.append(graph.enum_nodes[node])
            train_labels.append(labels)
        
        # create the train, val en test splits
        x_train, x_test, y_train, y_test = train_test_split(train_indices,
                                                            train_labels,
                                                            test_size=0.2,
                                                            random_state=1,
                                                            shuffle=True) 
        x_train, x_val, y_train, y_val = train_test_split(x_train,
                                                          y_train,
                                                          test_size=0.25,
                                                          random_state=1,
                                                          shuffle=True)

        self.x_train = torch.tensor(x_train)
        self.x_test = torch.tensor(x_test) 
        self.x_val = torch.tensor(x_val)
        self.y_val = torch.tensor(y_val)
        self.y_train = torch.tensor(y_train)
        self.y_test = torch.tensor(y_test)

To create the training data train_test_split from sklearn.model_selection is used. Importantly to note, is that in the training data, only node indices are include which have an entity type denoted. This is important for interpreting the overall performance of the model.

RGCNConv

In model.py a model setup is proposed with layers from PyTorch. Below, a copy of the code is included:

import torch

from torch import nn
from torch import Tensor, LongTensor
from torch_geometric.nn import RGCNConv


class RGCNModel(nn.Module):
    def __init__ (self, num_nodes: int,
                        emb_dim: int,
                        hidden_l: int,
                        num_rels: int,
                        num_classes: int) -> None:
    
        super(RGCNModel, self).__init__()
        self.embedding = nn.Embedding(num_nodes, emb_dim)
        self.rgcn1 = RGCNConv(in_channels=emb_dim,
                            out_channels=hidden_l,
                            num_relations=num_rels,
                            num_bases=None)
        self.rgcn2 = RGCNConv(in_channels=hidden_l,
                            out_channels=num_classes,
                            num_relations=num_rels,
                            num_bases=None)

        # intialize weights
        nn.init.kaiming_uniform_(self.rgcn1.weight, mode='fan_out', nonlinearity='relu')
        nn.init.kaiming_uniform_(self.rgcn2.weight, mode='fan_out', nonlinearity='relu')

    def forward(self, edge_index: LongTensor, edge_type: LongTensor) -> Tensor:
        x = self.rgcn1(self.embedding.weight, edge_index, edge_type)
        x = torch.relu(x)
        x = self.rgcn2(x, edge_index, edge_type)
        x = torch.sigmoid(x)
        return x

Besides the RGCNConv layers of PyTorch, the nn.Embedding layer is utilized. This layer creates an embedding tensor with a gradient. As the embedding tensor contains a gradient, it will be updated in backpropagation.

Two layers of R-GCN with a ReLU activation in between are used. This setup is proposed in literature[4][5]. As explained earlier, stacking two layers allows for node updates that take the node representations over two hops into account. The output of the first R-GCN layer contains updated node representations for each adjacent node. Through passing the update of the first layer, the node update of the second layers includes the updated representations of the first layers. Therefore, each node is updated with information over two hops.

In the forward pass, the Sigmoid activation is used over the output of the second R-GCN layer, because entities can have multiple type labels (multi-label classification). Each type class should be predicted for separately. In the case that multiple labels can be predicted, the Sigmoid activation is desired as we want to make a prediction for each label independently. We do not only predict the most likely label, the Softmax would be a better option.

Train the R-GCN model

To train the R-GCN model, the ModelTrainer class was created in train.py. __init__ stores the model and training parameters. Furthermore, the functions train_model() and compute_f1() are part of the class:

import torch

from sklearn.metrics import f1_score
from torch import nn, Tensor
from typing import List, Tuple

from graph import Graph
from trainingdata import TrainingData
from model import RGCNModel
from plot import plot_results

class ModelTrainer:
    def __init__(self,
                model: nn.Module,
                epochs: int,
                lr: float,
                weight_d: float) -> None:

        self.model = model
        self.epochs = epochs
        self.lr = lr
        self.weight_d = weight_d

    def compute_f1(self, graph: Graph, x: Tensor, y_true: Tensor) -> float:
        '''evaluate the model with the F1 samples metric'''
        pred = self.model(graph.edge_index, graph.edge_type)
        pred = torch.round(pred)
        y_pred = pred[x]
        # f1_score function does not accept torch tensor with gradient
        y_pred = y_pred.detach().numpy()
        f1_s = f1_score(y_true, y_pred, average='samples', zero_division=0)
        return f1_s
    
    def train_model(self, graph: Graph, training_data: TrainingData) -> Tuple[List[float]]:
        '''loop to train pytorch R-GCN model'''

        optimizer = torch.optim.Adam(self.model.parameters(), lr=self.lr, weight_decay=self.weight_d)
        loss_f = nn.BCELoss()

        f1_ss: list = []
        losses: list = []
    
        for epoch in range(self.epochs):
            
            # evaluate the model
            self.model.eval()
            f1_s = self.compute_f1(graph, training_data.x_val, training_data.y_val)
            f1_ss.append(f1_s)
            
            # train the model
            self.model.train()
            optimizer.zero_grad()
            out = self.model(graph.edge_index, graph.edge_type)
            output = loss_f(out[training_data.x_train], training_data.y_train)
            output.backward()
            optimizer.step()
            l = output.item()
            losses.append(l)
            
            # every tenth epoch print loss and F1 score
            if epoch%10==0:
                l = output.item()
                print(f'Epoch: {epoch}, Loss: {l:.4f}n',
                    f'F1 score on validation set:{f1_s:.2f}')

        return losses, f1_ss,

Let’s discuss some important aspects of train_model() . For calculating the loss, the Binary Cross Entropy Loss (BCELoss) calculation is used. BCELoss is a suitable loss calculation for multi-label classification combined with a Sigmoid activation on the output layer as it calculates the loss over each predicted label and the true label separately. Therefore, it treats each output unit of our model independently. This is desired as a node could have multiple entity types (Figure 2: Tarantino is a person and a director). However, if the graph only contained nodes with one entity type, the Softmax with a Categorical Cross Entropy Loss would be a better choice.

Another important aspect, is the evaluation of the prediction performance. The F1-score is a suitable metric as there are multiple classes to predict, which may occur in an imbalanced fashion. Imbalanced data means that some classes are represented more than others. The imbalanced data could result in a skewed performance of the model as only a few type classes may be predicted well. Therefore, it is desired to include the precision and recall in the performance evaluation which the F1-score does. The f1_score() of sklearn.metrics is used. To account for the imbalanced data distribution the method weighted-F1-score is used. The F1 score is calculated for each label separately. Then the F1 scores are averaged considering the proportion for each label in the dataset, resulting in the weighted-F1-score.

Start training

In the data folder on Github, are an example graph (example.nt) and a larger graph, called AIFB[7] (AIFB.nt). This dataset, amongst others, is used more often in research[5][6] on R-GCNs. To start training of the model, the following code is included in train.py:

if __name__=='__main__':
    file_path = './data/AIFB.nt' # adjust to use another dataset
    graph = Graph()
    graph.init_graph(file_path)
    graph.create_edge_data()
    graph.print_graph_statistics()

    training_data = TrainingData()
    training_data.create_training_data(graph)
    
    # training parameters
    emb_dim = 50
    hidden_l = 16
    epochs = 51
    lr = 0.01
    weight_d = 0.00005

    model = RGCNModel(len(graph.enum_nodes.keys()),
                        emb_dim,
                        hidden_l,
                        2*len(graph.enum_relations.keys())+1, # remember the inverse relations in the edge data
                        len(graph.enum_classes.keys()))

    trainer = ModelTrainer(model, epochs, lr, weight_d)
    losses, f1_ss = trainer.train_model(graph, training_data)
    
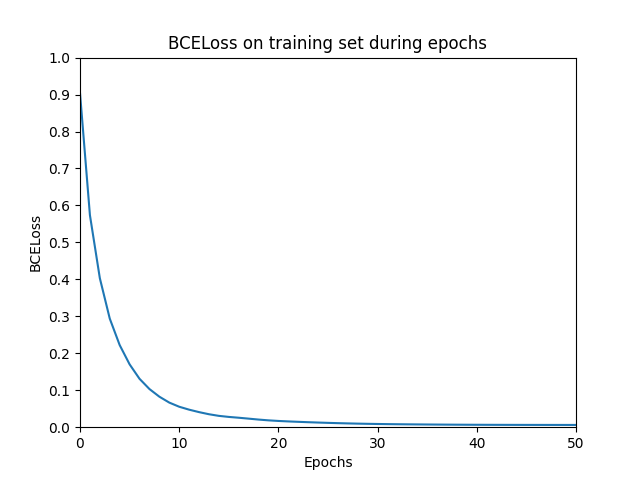
    plot_results(epochs, losses, title='BCELoss on trainig set during epochs', y_label='Loss')
    plot_results(epochs, f1_ss, title='F1 score on validation set during epochs', y_label='F1 samples')

    # evaluate model on test set and print result
    f1_s_test = trainer.compute_f1(graph, training_data.x_test, training_data.y_test)
    print(f'F1 score on test set = {f1_s_test}')

To setup an environment and run the code I refer to the readme in the repository on GitHub. Running the code will yield two plots: one with the BCELoss on the training set and one with the F1 score on the validation set.

If you have any comments or questions, please get in touch!

Remarks

1. rdf:type is used to create node labels. Literature[4][5] proposes a different prediction task with other labels that cannot be found in the AIFB graph itself. However the main principles, like creating the edge_index, edge_type and the prediction setup remain the same.
2. Functions to parse the graph data work for some specific graphs that I tested with. However, when using this code for other graphs, one should keep in mind the syntax of the input graph.
3. Training/model parameters such as learning rate, epochs, hidden layer and weight decay are found in literature[4][5].

References

[1] Manola, F., Miller, E., McBride, B.: RDF primer, W3C recommendation (2004), https://www.w3.org/TR/REC-rdf-syntax/

[2] Tiwari, S., Al-Aswadi, F.N., Gaurav, D.: Recent trends in knowledge graphs: theory and practice. Soft Computing 25(13), 8337–8355 (2021). https://doi.org/10.1007/s00500-021-05756-8

[3] Liu, W., Chang, S.F.: Robust multi-class transductive learning with graphs. In: 2009 IEEE Conference on Computer Vision and Pattern Recognition. pp. 381–388 (2009). https://doi.org/10.1109/CVPR.2009.5206871

[4] Schlichtkrull, M., Kipf, T.N., Bloem, P., van den Berg, R., Titov, I., Welling, M.: Modeling Relational Data with Graph Convolutional Networks. In: Gangemi, A., Navigli, R., Vidal, M.E., Hitzler, P., Troncy, R., Hollink, L., Tordai, A., Alam, M. (eds.) The Semantic Web. pp. 593–607. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93417-4 38

[5] Thanapalasingam, T., van Berkel, L., Bloem, P., Groth, P.: Rela- tional Graph Convolutional Networks: A Closer Look. arXiv preprint arXiv:2107.10015 (2021). https://doi.org/10.48550/ARXIV.2107.10015

[6] Bloehdorn, S., Sure, Y.: Kernel Methods for Mining Instance Data in On- tologies. In: The Semantic Web, pp. 58–71. Springer, Berlin, Heidelberg (2007)

Entity Type Prediction with Relational Graph Convolutional Network (PyTorch) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.