De-biasing Treatment Effects with Double Machine Learning

Causal AI, exploring the integration of causal reasoning into machine learning

What is this series of articles about?

Welcome to my series on Causal AI, where we will explore the integration of causal reasoning into machine learning models. Expect to explore a number of practical applications across different business contexts.

In the last article we explored making Causal Discovery work in real-world business settings. This time we will cover de-biasing treatment effects with Double Machine Learning.

If you missed the last article on Causal Discovery, check it out here:

Making Causal Discovery work in real-world business settings

Introduction

This article will demonstrate why Double Machine Learning is an essential part of the Causal AI toolbox:

Expect to gain a deep understanding of:

• Average treatment effects (ATE)
• The challenges of using Linear Regression to estimate ATE
• Double Machine Learning and how it overcomes the challenges Linear Regression faces
• A worked case study in Python illustrating how to apply Double Machine Learning.

The full notebook can be found here:

causal_ai/notebooks/estimating average treatment effects with double machine learning.ipynb at main · raz1470/causal_ai

Average Treatment Effects (ATE)

ATE

ATE is the average impact of a treatment or intervention on a population. We can calculate it by comparing the average change in a chosen metric between a treatment and control group.

For example, consider a marketing team is running a promotion. The treatment group consists of customers who receive an offer, while the control group consists of customers who didn’t. We can calculate ATE comparing the average number of orders in the treatment and control group.

Potential outcomes framework

The potential outcomes framework was developed by Donald Rubin and has become a foundational concept in causal inference. Lets try and understand it using the example above from the marketing team.

1. Treatment assignment: Each customer has two potential outcomes, the outcome of being in the treatment group (sent offer) and the outcome of being in the control group (not sent offer). However, only one potential outcome is observed for each customer.
2. Counterfactuals: The potential outcome which is not observed is a counterfactual e.g. what would have happened if this customer was in the control group (not sent offer).
3. Causal effect: The causal effect of a treatment is the difference between the potential outcomes under different treatment conditions (sent off vs not sent offer).
4. Estimation: Causal effects can be estimated using experimental or observational data using a range of causal techniques.

Several assumptions are made to help ensure the estimated effects are valid:

• Stable Unit Treatment Value Assumption (SUTVA): The potential outcome for any customer is unaffected by the treatment assignment of other customers.
• Positivity: For any combination of features, there must be some probability that a customer could receive either treatment or control
• Ignorability: All confounders which effects both treatment and outcome are observed.

Experimental data

Estimating ATE with experimental data is relatively straightforward.

Randomised Controlled Trials (RCTs) or AB tests are designed to randomly assign participants to treatment and control groups. This ensures that any differences in outcomes can be attributed to the treatment effect rather than pre-existing characteristics of the participants.

Back to the example from the marketing team. If they randomly split customers between the treatment and control group, the average difference in orders is the causal effect of the offer sent.

Observational data

Estimating ATE using observational data is more challenging.

The most common challenge is confounding variables which effect both the treatment and outcome. Failure to control for confounders will lead to biased estimates of the treatment effect. We will come back to this later in the article in the worked case study.

Other challenges include:

• Selection bias — The treatment assignment is influenced by factors related to the outcome.
• Heterogenous treatment effects — The treatment effect varies across different subgroups of the population.

Estimating ATE using Linear Regression

Overview

Linear regression can be used to estimate ATE using observational data. The treatment (T) and control features (X) are included as variables in the model.

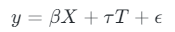
The coefficient of the treatment variable is the ATE — the average change in the outcome variable associated with a unit change in the treatment variable, while keeping control features constant.

Data-generating process

We can use a simple data-generating process with one outcome, treatment and confounder to illustrate how we can use linear regression to estimate ATE.

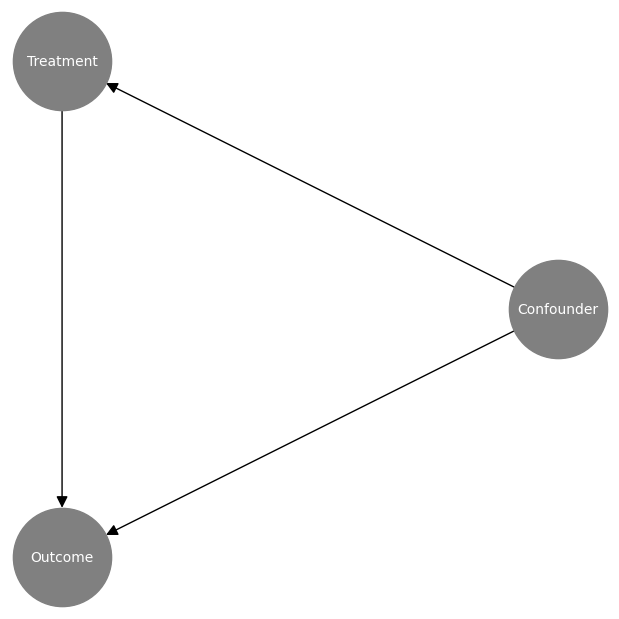
First of all we can visualise the causal graph:

# Create node lookup variables
node_lookup = {0: 'Confounder',
               1: 'Treatment',
               2: 'Outcome'                                                                                       
 }

total_nodes = len(node_lookup)

# Create adjacency matrix - this is the base for our graph
graph_actual = np.zeros((total_nodes, total_nodes))

# Create graph using expert domain knowledge
graph_actual[0, 1] = 1.0 # Confounder -> Treatment
graph_actual[0, 2] = 1.0 # Confounder -> Outcome
graph_actual[1, 2] = 1.0 # Treatment -> Outcome
     
plot_graph(input_graph=graph_actual, node_lookup=node_lookup)

And then we can create samples using the simple data-generating process. Pay close attention to the coefficient of the treatment variable (0.75) — this is our ground truth ATE.

np.random.seed(123)

# Create dataframe with a confounder, treatment and outcome
df = pd.DataFrame(columns=['Confounder', 'Treatment', 'Outcome'])
df['Confounder'] = np.random.normal(loc=100, scale=25, size=1000)
df['Treatment'] = np.random.normal(loc=50, scale=10, size=1000) + 0.50 * df['Confounder']
df['Outcome'] = 0.25 * df['Confounder'] + 0.75 * df['Treatment'] + np.random.normal(loc=0, scale=5, size=1000)

sns.pairplot(df, corner=True)

Linear regression

We can then train a linear regression model and extract the coefficient of the treatment variable — We can see that it correctly estimates the ATE (0.75).

# Set target and features
y = df['Outcome']
X = df[['Confounder', 'Treatment']]

# Train model 
model = RidgeCV()
model = model.fit(X, y)

# Extract the treatment coefficient
ate_lr = round(model.coef_[1], 2)

print(f'The average treatment effect using Linear Regression is: {ate_lr}')

Challenges

Linear regression can be a very effective method for estimating ATE. However, there are some challenges to be aware of:

• It struggles when we have high-dimensional data.
• The “nuisance parameters” (the control features which are a “nuisance” to estimate) may be too complex for linear regression to estimate.
• It assumes the treatment effect is constant across different subgroups of the population (e.g. no heterogeneity).
• Assumes no unobserved confounders.
• Assumes that the treatment effect is linear.

Double Machine Learning (DML)

Overview

Double Machine Learning is a causal method first introduced in 2017 in the paper “Double/Debiased Machine Learning for Treatment and Structural Parameters”:

Double/Debiased Machine Learning for Treatment and Causal Parameters

It aims to reduce bias and improve the estimation of causal effects in situations where we have high-dimensional data and/or complex nuisance parameters.

It is inspired by the Frisch-Waugh-Lovell theorem, so let’s start by understanding this.

Frisch-Waugh-Lovell theorem

The FWL theorem is used to decompose the effects of multiple regressors on an outcome variable, allowing us to isolate effects of interest.

Imagine you had two sets of features, X1 and X2. You could estimate the model parameters using linear regression like we did before. However, you can also get the same parameter for X1 by following these steps:

1. Use X2 only to predict the outcome
2. Use X2 only to predict X1
3. Calculate the residuals from the outcome model (step 1) and feature model (step 2)
4. Regress the residuals of the outcome model on the residuals of the feature model to estimate the parameter for X1

At first glance this can be quite hard to follow, so let’s try it out in Python to illustrate. We use the same data as before, but take the treatment column as X1 and the confounder column as X2:

# Set treatment, outcome and confounder samples
treatment = df['Treatment'].to_numpy().reshape(-1,1)
outcome = df['Outcome'].to_numpy().reshape(-1,1)
confounder = df['Confounder'].to_numpy().reshape(-1,1)

# Train treatment model and calculate residuals
treatment_model = RidgeCV()
treatment_model = treatment_model.fit(confounder, treatment)
treatment_pred = treatment_model.predict(confounder)
treatment_residuals = treatment - treatment_pred

# Train outcome model and calculate residuals
outcome_model = RidgeCV()
outcome_model = outcome_model.fit(confounder, outcome)
outcome_pred = outcome_model.predict(confounder)
outcome_residuals = outcome - outcome_pred

# Train residual model and calculate average treatment effect
final_model = RidgeCV()
final_model = final_model.fit(treatment_residuals, outcome_residuals)
ate_dml = round(final_model.coef_[0][0], 2)

print(f'The average treatment effect is: {ate_fwl}')

We can see that it correctly estimates the coefficient of the treatment variable (0.75).

Double Machine Learning

Double Machine Learning builds upon FWL by isolating the effects of treatment and control features and by using flexible machine learning models.

The first stage is often referred to an orthogonalization as the nuisance parameters are estimated independently of the treatment effect estimation.

First stage:

• Treatment model (de-biasing): Machine learning model used to estimate the probability of treatment assignment (often referred to as propensity score). The treatment model residuals are then calculated.
• Outcome model (de-noising): Machine learning model used to estimate the outcome using just the control features. The outcome model residuals are then calculated.

Second stage:

• The treatment model residuals are used to predict the outcome model residuals.

The coefficient of the second stage model is the ATE. It is worth noting that the second stage model is a linear model, meaning we are assuming our treatment effect is linear (this is why we call DML a partially linear model).

Rather than code it up ourselves we can use the Microsoft package EconML. EconML has a wide range of Causal ML techniques implemented including a number of implementations of DML:

Welcome to econml’s documentation! – econml 0.15.0 documentation

# Train DML model
dml = LinearDML(discrete_treatment=False)
dml.fit(df['Outcome'].to_numpy().reshape(-1,1), T=df['Treatment'].to_numpy().reshape(-1,1), X=None, W=df['Confounder'].to_numpy().reshape(-1,1))

# Calculate average treatment effect
ate_dml = round(dml.ate()[0], 2)

print(f'The average treatment effect using the DML is: {ate_dml}')

We again can see that it correctly estimates the coefficient of the treatment variable (0.75).

Marketing Case Study

Background

The Marketing team send attractive offers to selected customers. They don’t currently hold out a randomly selected sample of customers to measure the impact of the offers.

The Data Science team is asked to estimate how the offers affect customer orders.

Confounding bias

Naively comparing customers who were and weren’t sent offers is biased. This is driven by confounding factors:

• Customers who opt-out of email can’t receive an offer – this population is less engaged and less likely to order.
• The CRM team target customers based on their order history — order history effects how likely you are to order again.

Data generating process

We set up a data generating process with the following characteristics:

• Difficult nuisance parameters
• Simple treatment effect (no heterogeneity)

The X features are customer characteristics taken before the treatment:

T is a binary flag indicating whether the customer received the offer.

np.random.seed(123)

# Set number of observations
n=100000

# Set number of features
p=10

# Create features
X = np.random.uniform(size=n * p).reshape((n, -1))

# Nuisance parameters
b = (
    np.sin(np.pi * X[:, 0] * X[:, 1])
    + 2 * (X[:, 2] - 0.5) ** 2
    + X[:, 3]
    + 0.5 * X[:, 4]
    + X[:, 5] * X[:, 6]
    + X[:, 7] ** 3
    + np.sin(np.pi * X[:, 8] * X[:, 9])
)

# Create binary treatment
T = np.random.binomial(1, expit(b))

# Set treatment effect
tau = 0.75

# Calculate outcome
y = b + T * tau + np.random.normal(size=n)

The data generating process python code is based on the synthetic data creator from Ubers Causal ML package. Being able to create realistic synthetic data is crucial when it comes to assessing causal inference methods so I highly recommend you check it out:

causalml/causalml/dataset/regression.py at master · uber/causalml

Linear Regression

We start by using linear regression to estimate the ATE. Our expectation is that it will struggle to capture the nuisance parameters and then potentially mis-specify the treatment effect.

# Append features and treatment
X_T = np.append(X, T.reshape(-1, 1), axis=1)

# Train linear regression model 
model = RidgeCV()
model = model.fit(X_T, y)
y_pred = model.predict(X_T)

# Extract the treatment coefficient
ate_lr = round(model.coef_[-1], 2)

print(f'The average treatment effect using Linear Regression is: {ate_lr}')

Double Machine Learning

We then train a DML model using LightGBM as flexible first stage models. This should allow us to capture the difficult nuisance parameters whilst correctly calculating the treatment effect.

np.random.seed(123)

# Train DML model using flexible stage 1 models
dml = LinearDML(model_y=LGBMRegressor(), model_t=LGBMClassifier(), discrete_treatment=True)
dml.fit(y, T=T, X=None, W=X)

# Calculate average treatment effect
ate_dml = round(dml.ate(), 2)

print(f'The average treatment effect using the DML is: {ate_dml}')

Comparison

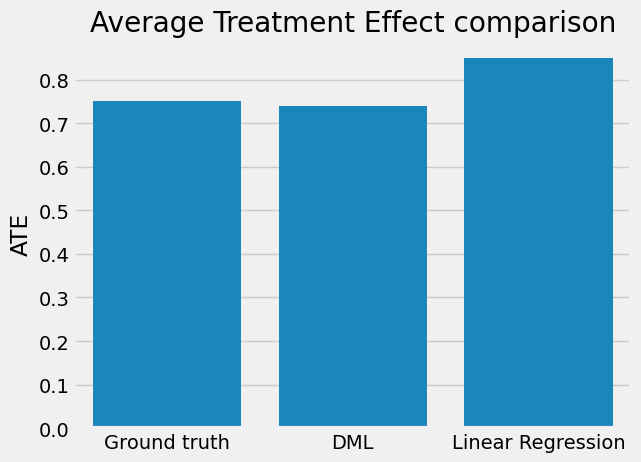
When we compare the results, we observe that linear regression gives us a biased estimate whilst DML is very close to the ground truth. This really shows the power of DML!

# Plot comparison of results
categories = ['Ground truth', 'DML', 'Linear Regression']
sns.barplot(x=categories, y=[tau, ate_dml, ate_lr])
plt.ylabel('ATE')
plt.title('Average Treatment Effect comparison')
plt.show()

Other methods

There a several other causal methods which we can use to estimate ATE (a lot of which are implemented in both EconML and CausalML packages):

• Propensity score matching (PSM)
• Inverse-propensity score matching (IPSM)
• S-Learner
• T-Learner
• Doubly-Robust Learner (DR)
• Instrument variable learner (IV)

If you want to delve into these methods further, I would recommend starting with the S-Learner and T-Learner (often referred to as meta-learners). A couple of key learnings to help you start to work out when and where you could apply them:

• When your treatment is binary, and your treatment and control size is equally balanced, the T-Learner is often a simpler alternative to DML.
• When your treatment is continuous, and you suspect the treatment effect may be non-linear, the S-Learner may be more appropriate than DML.
• Meta-learners can struggle with regularization bias (particularly the S-learner) — When we do see DML outperform meta-learners, this is usually the reason.

Follow me if you want to continue this journey into Causal AI — In the next article we will explore how we can estimate Conditional Average Treatment Effects (CATE) with Double Machine Learning to help us personalise treatments at a customer level.

De-biasing Treatment Effects with Double Machine Learning was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.