Category: Technology
-
Samsung expands its AI Home technology to new appliances, and there’s one I’m beelining for at CES
This tiny Mirumi robot straps to your bag and looks around.Samsung expands its AI Home technology to new appliances, and there’s one I’m beelining for at CESSamsung expands its AI Home technology to new appliances, and there’s one I’m beelining for at CES -
Loads of fresh content is coming to Warhammer 40,000: Space Marine 2 in 2025
Everything you need to know about Warhammer 40,000: Space Marine 2 in 2025.Originally appeared here:
Loads of fresh content is coming to Warhammer 40,000: Space Marine 2 in 2025 -

Wake Up Dead Man: A Knives Out Mystery: everything we know so far about Netflix’s Knives Out 3 movie
 Here’s what we know so far about Wake Up Dead Man: A Knives Out Mystery ahead of its arrival on Netflix.Wake Up Dead Man: A Knives Out Mystery: everything we know so far about Netflix’s Knives Out 3 movieWake Up Dead Man: A Knives Out Mystery: everything we know so far about Netflix’s Knives Out 3 movie
Here’s what we know so far about Wake Up Dead Man: A Knives Out Mystery ahead of its arrival on Netflix.Wake Up Dead Man: A Knives Out Mystery: everything we know so far about Netflix’s Knives Out 3 movieWake Up Dead Man: A Knives Out Mystery: everything we know so far about Netflix’s Knives Out 3 movie -

The Samsung Galaxy Watch 8 could bring the Classic model back
 An industry database suggests one of Samsung’s 2025 smartwatches will be the Galaxy 8 Classic.
An industry database suggests one of Samsung’s 2025 smartwatches will be the Galaxy 8 Classic.Go Here to Read this Fast! The Samsung Galaxy Watch 8 could bring the Classic model back
Originally appeared here:
The Samsung Galaxy Watch 8 could bring the Classic model back -
US Treasury declares ‘major incident’ after apparent state-sponsored Chinese hack
Documents reportedly stolen in security breach targeting the US Treasury Department.Originally appeared here:
US Treasury declares ‘major incident’ after apparent state-sponsored Chinese hack -
Paradigm Shifts of Eval in the Age of LLM
Paradigm Shifts of Eval in the Age of LLMs
LLMs requires some subtle, conceptually simple, yet important changes in the way we think about evaluation
I’ve been building evaluation for ML systems throughout my career. As head of data science at Quora, we built eval for feed ranking, ads, content moderation, etc. My team at Waymo built eval for self-driving cars. Most recently, at our fintech startup Coverbase, we use LLMs to ease the pain of third-party risk management. Drawing from these experiences, I’ve come to recognize that LLMs requires some subtle, conceptually simple, yet important changes in the way we think about evaluation.
The goal of this blog post is not to offer specific eval techniques to your LLM application, but rather to suggest these 3 paradigm shifts:
- Evaluation is the cake, no longer the icing.
- Benchmark the difference.
- Embrace human triage as an integral part of eval.
I should caveat that my discussion is focused on LLM applications, not foundational model development. Also, despite the title, much of what I discuss here is applicable to other generative systems (inspired by my experience in autonomous vehicles), not just LLM applications.
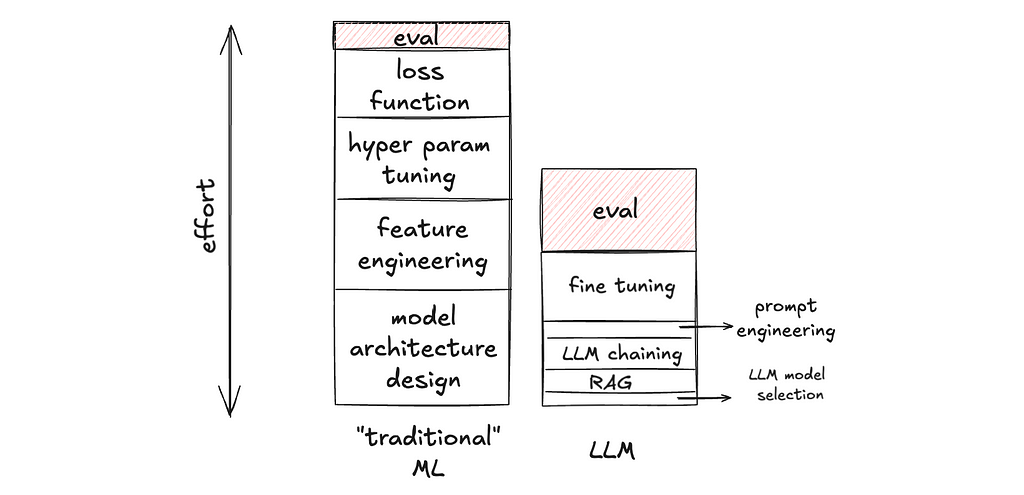
1. Evaluation is the cake, no longer the icing.
Evaluation has always been important in ML development, LLM or not. But I’d argue that it is extra important in LLM development for two reasons:
a) The relative importance of eval goes up, because there are lower degrees of freedom in building LLM applications, making time spent non-eval work go down. In LLM development, building on top of foundational models such as OpenAI’s GPT or Anthropic’s Claude models, there are fewer knobs available to tweak in the application layer. And these knobs are much faster to tweak (caveat: faster to tweak, not necessarily faster to get it right). For example, changing the prompt is arguably much faster to implement than writing a new hand-crafted feature for a Gradient-Boosted Decision Tree. Thus, there is less non-eval work to do, making the proportion of time spent on eval go up.

b) The absolute importance of eval goes up, because there are higher degrees of freedom in the output of generative AI, making eval a more complex task. In contrast with classification or ranking tasks, generative AI tasks (e.g. write an essay about X, make an image of Y, generate a trajectory for an autonomous vehicle) can have an infinite number of acceptable outputs. Thus, the measurement is a process of projecting a high-dimensional space into lower dimensions. For example, for an LLM task, one can measure: “Is output text factual?”, “Does the output contain harmful content?”, “Is the language concise?”, “Does it start with ‘certainly!’ too often?”, etc. If precision and recall in a binary classification task are loss-less measurements of those binary outputs (measuring what you see), the example metrics I listed earlier for an LLM task are lossy measurements of the output text (measuring a low-dimensional representation of what you see). And that is much harder to get right.
This paradigm shift has practical implications on team sizing and hiring when staffing a project on LLM application.
2. Benchmark the difference.
This is the dream scenario: we climb on a target metric and keep improving on it.
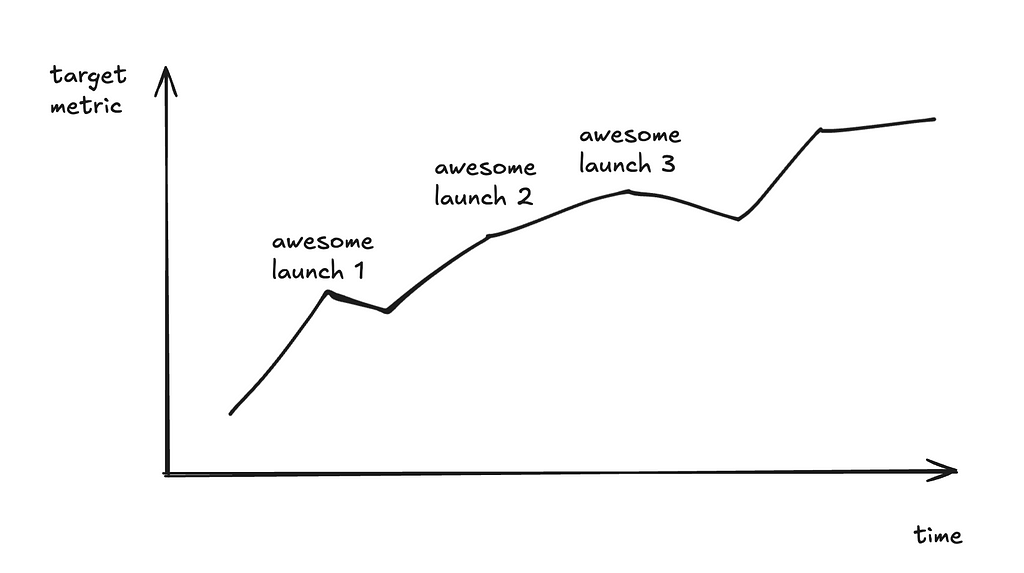
The reality?
You can barely draw more than 2 consecutive points in the graph!
These might sound familiar to you:
After the 1st launch, we acquired a much bigger dataset, so the new metric number is no longer an apple-to-apple comparison with the old number. And we can’t re-run the old model on the new dataset — maybe other parts of the system have upgraded and we can’t check out the old commit to reproduce the old model; maybe the eval metric is an LLM-as-a-judge and the dataset is huge, so each eval run is prohibitively expensive, etc.
After the 2nd launch, we decided to change the output schema. For example, previously, we instructed the model to output a yes / no answer; now we instruct the model to output yes / no / maybe / I don’t know. So the previously carefully curated ground truth set is no longer valid.
After the 3rd launch, we decided to break the single LLM calls into a composite of two calls, and we need to evaluate the sub-component. We need new datasets for sub-component eval.
….
The point is the development cycle in the age of LLMs is often too fast for longitudinal tracking of the same metric.
So what is the solution?
Measure the delta.
In other words, make peace with having just two consecutive points on that graph. The idea is to make sure each model version is better than the previous version (to the best of your knowledge at that point in time), even though it is quite hard to know where its performance stands in absolute terms.
Suppose I have an LLM-based language tutor that first classifies the input as English or Spanish, and then offers grammar tips. A simple metric can be the accuracy of the “English / Spanish” label. Now, say I made some changes to the prompt and want to know whether the new prompt improves accuracy. Instead of hand-labeling a large data set and computing accuracy on it, another way is to just focus on the data points where the old and new prompts produce different labels. I won’t be able to know the absolute accuracy of either model this way, but I will know which model has higher accuracy.
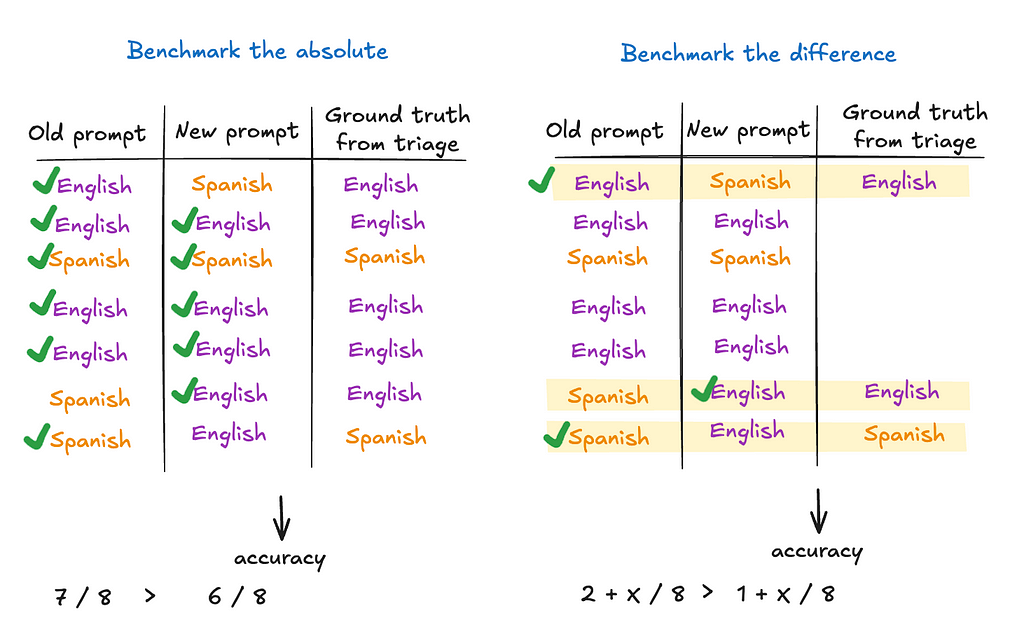
I should clarify that I am not saying benchmarking the absolute has no merits. I am only saying we should be cognizant of the cost of doing so, and benchmarking the delta — albeit not a full substitute — can be a much more cost-effective way to get a directional conclusion. One of the more fundamental reasons for this paradigm shift is that if you are building your ML model from scratch, you often have to curate a large training set anyway, so the eval dataset can often be a byproduct of that. This is not the case with zero-shot and few-shots learning on pre-trained models (such as LLMs).
As a second example, perhaps I have an LLM-based metric: we use a separate LLM to judge whether the explanation produced in my LLM language tutor is clear enough. One might ask, “Since the eval is automated now, is benchmarking the delta still cheaper than benchmarking the absolute?” Yes. Because the metric is more complicated now, you can keep improving the metric itself (e.g. prompt engineering the LLM-based metric). For one, we still need to eval the eval; benchmarking the deltas tells you whether the new metric version is better. For another, as the LLM-based metric evolves, we don’t have to sweat over backfilling benchmark results of all the old versions of the LLM language tutor with the new LLM-based metric version, if we only focus on comparing two adjacent versions of the LLM language tutor models.
Benchmarking the deltas can be an effective inner-loop, fast-iteration mechanism, while saving the more expensive way of benchmarking the absolute or longitudinal tracking for the outer-loop, lower-cadence iterations.
3. Embrace human triage as an integral part of eval.
As discussed above, the dream of carefully triaging a golden set once-and-for-all such that it can be used as an evergreen benchmark can be unattainable. Triaging will be an integral, continuous part of the development process, whether it is triaging the LLM output directly, or triaging those LLM-as-judges or other kinds of more complex metrics. We should continue to make eval as scalable as possible; the point here is that despite that, we should not expect the elimination of human triage. The sooner we come to terms with this, the sooner we can make the right investments in tooling.
As such, whatever eval tools we use, in-house or not, there should be an easy interface for human triage. A simple interface can look like the following. Combined with the point earlier on benchmarking the difference, it has a side-by-side panel, and you can easily flip through the results. It also should allow you to easily record your triaged notes such that they can be recycled as golden labels for future benchmarking (and hence reduce future triage load).
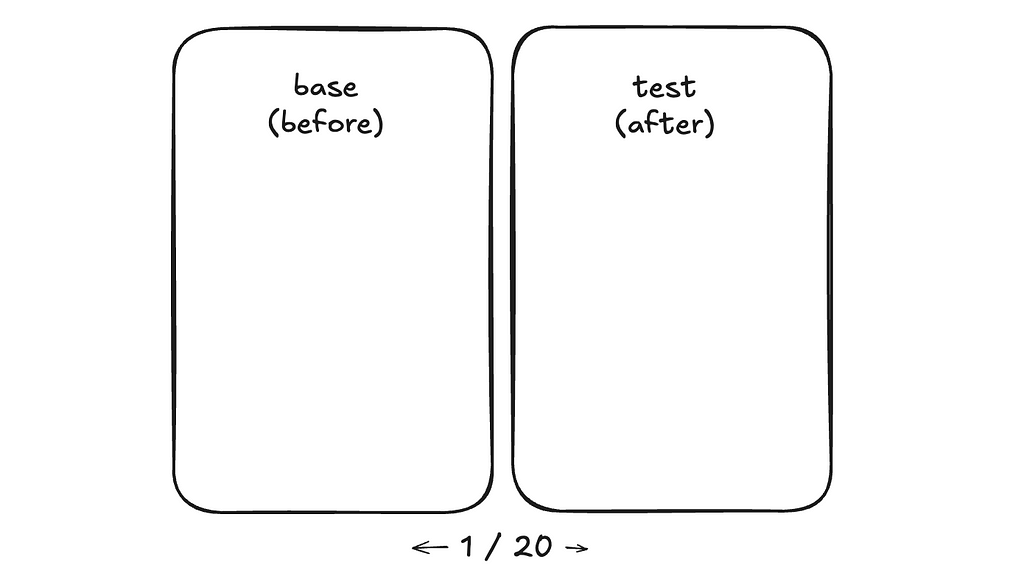
A more advanced version ideally would be a blind test, where it is unknown to the triager which side is which. We’ve repeatedly confirmed with data that when not doing blind testing, developers, even with the best intentions, have subconscious bias, favoring the version they developed.
These three paradigm shifts, once spotted, are fairly straightforward to adapt to. The challenge isn’t in the complexity of the solutions, but in recognizing them upfront amidst the excitement and rapid pace of development. I hope sharing these reflections helps others who are navigating similar challenges in their own work.
Paradigm Shifts of Eval in the Age of LLM was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Paradigm Shifts of Eval in the Age of LLMGo Here to Read this Fast! Paradigm Shifts of Eval in the Age of LLM
-
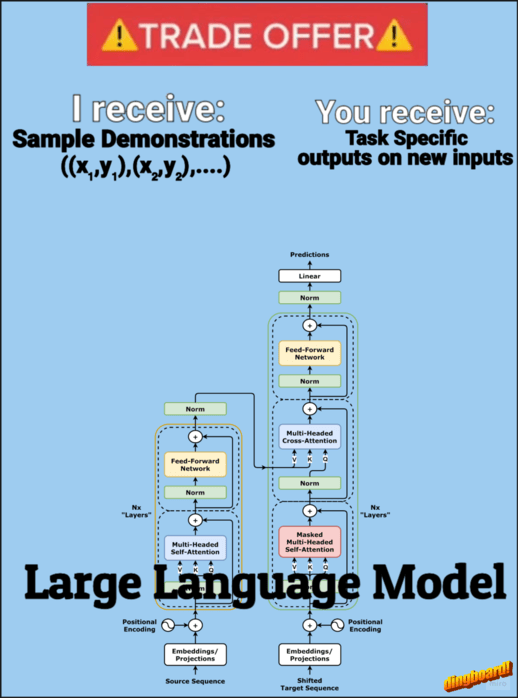
The Math Behind In-Context Learning
From attention to gradient descent: unraveling how transformers learn from examples
In-context learning (ICL) — a transformer’s ability to adapt its behavior based on examples provided in the input prompt — has become a cornerstone of modern LLM usage. Few-shot prompting, where we provide several examples of a desired task, is particularly effective at showing an LLM what we want it to do. But here’s the interesting part: why can transformers so easily adapt their behavior based on these examples? In this article, I’ll give you an intuitive sense of how transformers might be pulling off this learning trick.

Source: Image by Author (made using dingboard) This will provide a high-level introduction to potential mechanisms behind in-context learning, which may help us better understand how these models process and adapt to examples.
The core goal of ICL can be framed as: given a set of demonstration pairs ((x,y) pairs), can we show that attention mechanisms can learn/implement an algorithm that forms a hypothesis from these demonstrations to correctly map new queries to their outputs?
Softmax Attention
Let’s recap the basic softmax attention formula,

Source: Image by Author We’ve all heard how temperature affects model outputs, but what’s actually happening under the hood? The key lies in how we can modify the standard softmax attention with an inverse temperature parameter. This single variable transforms how the model allocates its attention — scaling the attention scores before they go through softmax changes the distribution from soft to increasingly sharp. This would slightly modify the attention formula as,
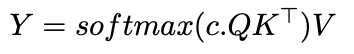
Source: Image by Author Where c is our inverse temperature parameter. Consider a simple vector z = [2, 1, 0.5]. Let’s see how softmax(c*z) behaves with different values of c:
When c = 0:
- softmax(0 * [2, 1, 0.5]) = [0.33, 0.33, 0.33]
- All tokens receive equal attention, completely losing the ability to discriminate between similarities
When c = 1:
- softmax([2, 1, 0.5]) ≈ [0.59, 0.24, 0.17]
- Attention is distributed proportionally to similarity scores, maintaining a balance between selection and distribution
When c = 10000 (near infinite):
- softmax(10000 * [2, 1, 0.5]) ≈ [1.00, 0.00, 0.00]
- Attention converges to a one-hot vector, focusing entirely on the most similar token — exactly what we need for nearest neighbor behavior
Now here’s where it gets interesting for in-context learning: When c is tending to infinity, our attention mechanism essentially becomes a 1-nearest neighbor search! Think about it — if we’re attending to all tokens except our query, we’re basically finding the closest match from our demonstration examples. This gives us a fresh perspective on ICL — we can view it as implementing a nearest neighbor algorithm over our input-output pairs, all through the mechanics of attention.
But what happens when c is finite? In that case, attention acts more like a Gaussian kernel smoothing algorithm where it weights each token proportional to their exponential similarity.
We saw that Softmax can do nearest neighbor, great, but what’s the point in knowing that? Well if we can say that the transformer can learn a “learning algorithm” (like nearest neighbor, linear regression, etc.), then maybe we can use it in the field of AutoML and just give it a bunch of data and have it find the best model/hyperparameters; Hollmann et al. did something like this where they train a transformer on many synthetic datasets to effectively learn the entire AutoML pipeline. The transformer learns to automatically determine what type of model, hyperparameters, and training approach would work best for any given dataset. When shown new data, it can make predictions in a single forward pass — essentially condensing model selection, hyperparameter tuning, and training into one step.
In 2022, Anthropic released a paper where they showed evidence that induction head might constitute the mechanism for ICL. What are induction heads? As stated by Anthropic — “Induction heads are implemented by a circuit consisting of a pair of attention heads in different layers that work together to copy or complete patterns.”, simply put what the induction head does is given a sequence like — […, A, B,…, A] it will complete it with B with the reasoning that if A is followed by B earlier in the context, it is likely that A is followed by B again. When you have a sequence like “…A, B…A”, the first attention head copies previous token info into each position, and the second attention head uses this info to find where A appeared before and predict what came after it (B).
Recently a lot of research has shown that transformers could be doing ICL through gradient descent (Garg et al. 2022, Oswald et al. 2023, etc) by showing the relation between linear attention and gradient descent. Let’s revisit least squares and gradient descent,

Source: Image by Author Now let’s see how this links with linear attention
Linear Attention
Here we treat linear attention as same as softmax attention minus the softmax operation. The basic linear attention formula,
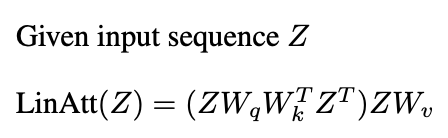
Source: Image by Author Let’s start with a single-layer construction that captures the essence of in-context learning. Imagine we have n training examples (x₁,y₁)…(xₙ,yₙ), and we want to predict y_{n+1} for a new input x_{n+1}.

Source: Image by Author This looks very similar to what we got with gradient descent, except in linear attention we have an extra term ‘W’. What linear attention is implementing is something known as preconditioned gradient descent (PGD), where instead of the standard gradient step, we modify the gradient with a preconditioning matrix W,
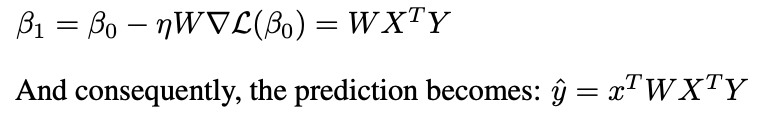
Source: Image by Author What we have shown here is that we can construct a weight matrix such that one layer of linear attention will do one step of PGD.
Conclusion
We saw how attention can implement “learning algorithms”, these are algorithms where basically if we provide lots of demonstrations (x,y) then the model learns from these demonstrations to predict the output of any new query. While the exact mechanisms involving multiple attention layers and MLPs are complex, researchers have made progress in understanding how in-context learning works mechanistically. This article provides an intuitive, high-level introduction to help readers understand the inner workings of this emergent ability of transformers.
To read more on this topic, I would suggest the following papers:
In-context Learning and Induction Heads
What Can Transformers Learn In-Context? A Case Study of Simple Function Classes
Transformers Learn In-Context by Gradient Descent
Transformers learn to implement preconditioned gradient descent for in-context learning
Acknowledgment
This blog post was inspired by coursework from my graduate studies during Fall 2024 at University of Michigan. While the courses provided the foundational knowledge and motivation to explore these topics, any errors or misinterpretations in this article are entirely my own. This represents my personal understanding and exploration of the material.
The Math Behind In-Context Learning was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The Math Behind In-Context LearningGo Here to Read this Fast! The Math Behind In-Context Learning
-

The Key to Smarter Models: Tracking Feature Histories

Capture context and improve predictions with historical data
Originally appeared here:
The Key to Smarter Models: Tracking Feature HistoriesGo Here to Read this Fast! The Key to Smarter Models: Tracking Feature Histories
-
LG announced its new lineup of ‘Hybrid AI’ Gram laptops, and they’re thinner than ever
LG’s 2025 Gram Pro laptops include the company’s first-ever Copilot+ PC, armed with the ‘Lunar Lake’ Intel Core Ultra processor.LG announced its new lineup of ‘Hybrid AI’ Gram laptops, and they’re thinner than everLG announced its new lineup of ‘Hybrid AI’ Gram laptops, and they’re thinner than ever -
3 great British crime shows to watch on New Year’s Eve
It’s almost 2025, so why don’t you ring in the new year with these three great British crime shows?Go Here to Read this Fast! 3 great British crime shows to watch on New Year’s Eve
Originally appeared here:
3 great British crime shows to watch on New Year’s Eve