
Originally appeared here:
Deploy a Microsoft Teams gateway for Amazon Q, your business expert
Go Here to Read this Fast! Deploy a Microsoft Teams gateway for Amazon Q, your business expert

Originally appeared here:
Deploy a Microsoft Teams gateway for Amazon Q, your business expert
Go Here to Read this Fast! Deploy a Microsoft Teams gateway for Amazon Q, your business expert
Large language models have been around for several years, but it wasn’t until 2023 that their presence became truly ubiquitous both within and outside machine learning communities. Previously opaque concepts like fine-tuning and RAG have gone mainstream, and companies big and small have been either building or integrating LLM-powered tools into their workflows.
As we look ahead at what 2024 might bring, it seems all but certain that these models’ footprint is poised to grow further, and that alongside exciting innovations, they’ll also generate new challenges for practitioners. The standout posts we’re highlighting this week point at some of these emerging aspects of working with LLMs; whether you’re relatively new to the topic or have already experimented extensively with these models, you’re bound to find something here to pique your curiosity.
As always, the range and depth of topics our authors covered in recent weeks is staggering—here’s a representative sample of must-reads:
Thank you for supporting the work of our authors! If you’re feeling inspired to join their ranks, why not write your first post? We’d love to read it.
Until the next Variable,
TDS Team
The New Frontiers of LLMs: Challenges, Solutions, and Tools was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The New Frontiers of LLMs: Challenges, Solutions, and Tools
Go Here to Read this Fast! The New Frontiers of LLMs: Challenges, Solutions, and Tools
Another opportunity to explore even more useful functionalities of pandas
Originally appeared here:
Level Up Your Pandas Game with These 15 Hidden Gems
Go Here to Read this Fast! Level Up Your Pandas Game with These 15 Hidden Gems


A remarkable new AI system called AlphaGeometry recently solved difficult high school-level math problems that stump most humans. By…
Originally appeared here:
The Future is Neuro-Symbolic: How AI Reasoning is Evolving
Go Here to Read this Fast! The Future is Neuro-Symbolic: How AI Reasoning is Evolving



Enriching network events with IP geolocation information is a crucial task, especially for organizations like the Canadian Centre for Cyber Security, the national CSIRT of Canada. In this article, we will demonstrate how to optimize Spark SQL joins, specifically focusing on scenarios involving non-equality conditions — a common challenge when working with IP geolocation data.
As cybersecurity practitioners, our reliance on enriching network events with IP geolocation databases necessitates efficient strategies for handling non-equi joins. While numerous articles shed light on various join strategies supported by Spark, the practical application of these strategies remains a prevalent concern for professionals in the field.
David Vrba’s insightful article, “About Joins in Spark 3.0”, published on Towards Data Science, serves as a valuable resource. It explains the conditions guiding Spark’s selection of specific join strategies. In his article, David briefly suggests that optimizing non-equi joins involves transforming them into equi-joins.
This write-up aims to provide a practical guide for optimizing the performance of a non-equi JOIN, with a specific focus on joining with IP ranges in a geolocation table.
To exemplify these optimizations, we will revisit the geolocation table introduced in our previous article.
+----------+--------+---------+-----------+-----------+
| start_ip | end_ip | country | city | owner |
+----------+--------+---------+-----------+-----------+
| 1 | 2 | ca | Toronto | Telus |
| 3 | 4 | ca | Quebec | Rogers |
| 5 | 8 | ca | Vancouver | Bell |
| 10 | 14 | ca | Montreal | Telus |
| 19 | 22 | ca | Ottawa | Rogers |
| 23 | 29 | ca | Calgary | Videotron |
+----------+--------+---------+-----------+-----------+
To illustrate Spark’s execution of an equi-join, we’ll initiate our exploration by considering a hypothetical scenario. Suppose we have a table of events, each event being associated with a specific ownerdenoted by the event_owner column.
+------------+--------------+
| event_time | event_owner |
+------------+--------------+
| 2024-01-01 | Telus |
| 2024-01-02 | Bell |
| 2024-01-03 | Rogers |
| 2024-01-04 | Videotron |
| 2024-01-05 | Telus |
| 2024-01-06 | Videotron |
| 2024-01-07 | Rogers |
| 2024-01-08 | Bell |
+------------+--------------+
Let’s take a closer look at how Spark handles this equi-join:
SELECT
*
FROM
events
JOIN geolocation
ON (event_owner = owner)
In this example, the equi-join is established between the events table and the geolocation table. The linking criterion is based on the equality of the event_owner column in the events table and the owner column in the geolocation table.
As explained by David Vrba in his blog post:
Spark will plan the join with SMJ if there is an equi-condition and the joining keys are sortable
Spark will execute a Sort Merge Join, distributing the rows of the two tables by hashing the event_owner on the left side and the owner on the right side. Rows from both tables that hash to the same Spark partition will be processed by the same Spark task—a unit of work. For example, Task-1 might receive:
+----------+-------+---------+-----------+-----------+
| start_ip | end_ip| country | city | owner |
+----------+-------+---------+-----------+-----------+
| 1 | 2 | ca | Toronto | Telus |
| 10 | 14 | ca | Montreal | Telus |
+----------+-------+---------+-----------+-----------+
+------------+--------------+
| event_time | event_owner |
+------------+--------------+
| 2024-01-01 | Telus |
| 2024-01-05 | Telus |
+------------+--------------+
Notice how Task-1 handles only a subset of the data. The join problem is divided into multiple smaller tasks, where only a subset of the rows from both the left and right sides is required. Furthermore, the left and right side rows processed by Task-1 have to match. This is true because every occurrence of “Telus” will hash to the same partition, regardless of whether it comes from the events or geolocation tables. We can be certain that no other Task-X will have rows with an owner of “Telus”.
Once the data is divided as shown above, Spark will sort both sides, hence the name of the join strategy, Sort Merge Join. The merge is performed by taking the first row on the left and testing if it matches the right. Once the rows on the right no longer match, Spark will pull rows from the left. It will keep dequeuing each side until no rows are left on either side.
Now that we have a better understanding of how equi-joins are performed, let’s contrast it with a non-equi join. Suppose we have events with an event_ip, and we want to add geolocation information to this table.
+------------+----------+
| event_time | event_ip |
+------------+----------+
| 2024-01-01 | 6 |
| 2024-01-02 | 14 |
| 2024-01-03 | 18 |
| 2024-01-04 | 27 |
| 2024-01-05 | 9 |
| 2024-01-06 | 23 |
| 2024-01-07 | 15 |
| 2024-01-08 | 1 |
+------------+----------+
To execute this join, we need to determine the IP range within which the event_ip falls. We accomplish this with the following condition:
SELECT
*
FROM
events
JOIN geolocation
ON (event_ip >= start_ip and event_ip <= end_ip)
Now, let’s consider how Spark will execute this join. On the right side (the geolocation table), there is no key by which Spark can hash and distribute the rows. It is impossible to divide this problem into smaller tasks that can be distributed across the compute cluster and performed in parallel.
In a situation like this, Spark is forced to employ more resource-intensive join strategies. As stated by David Vrba:
If there is no equi-condition, Spark has to use BroadcastNestedLoopJoin (BNLJ) or cartesian product (CPJ).
Both of these strategies involve brute-forcing the problem; for every row on the left side, Spark will test the “between” condition on every single row of the right side. It has no other choice. If the table on the right is small enough, Spark can optimize by copying the right-side table to every task reading the left side, a scenario known as the BNLJ case. However, if the left side is too large, each task will need to read both the right and left sides of the table, referred to as the CPJ case. In either case, both strategies are highly costly.
So, how can we improve this situation? The trick is to introduce an equality in the join condition. For example, we could simply unroll all the IP ranges in the geolocation table, producing a row for every IP found in the IP ranges.
This is easily achievable in Spark; we can execute the following SQL to unroll all the IP ranges:
SELECT
country,
city,
owner,
explode(sequence(start_ip, end_ip)) AS ip
FROM
geolocation
The sequence function creates an array with the IP values from start_ip to end_ip. The explode function unrolls this array into individual rows.
+---------+---------+---------+-----------+
| country | city | owner | ip |
+---------+---------+---------+-----------+
| ca | Toronto | Telus | 1 |
| ca | Toronto | Telus | 2 |
| ca | Quebec | Rogers | 3 |
| ca | Quebec | Rogers | 4 |
| ca | Vancouver | Bell | 5 |
| ca | Vancouver | Bell | 6 |
| ca | Vancouver | Bell | 7 |
| ca | Vancouver | Bell | 8 |
| ca | Montreal | Telus | 10 |
| ca | Montreal | Telus | 11 |
| ca | Montreal | Telus | 12 |
| ca | Montreal | Telus | 13 |
| ca | Montreal | Telus | 14 |
| ca | Ottawa | Rogers | 19 |
| ca | Ottawa | Rogers | 20 |
| ca | Ottawa | Rogers | 21 |
| ca | Ottawa | Rogers | 22 |
| ca | Calgary | Videotron | 23 |
| ca | Calgary | Videotron | 24 |
| ca | Calgary | Videotron | 25 |
| ca | Calgary | Videotron | 26 |
| ca | Calgary | Videotron | 27 |
| ca | Calgary | Videotron | 28 |
| ca | Calgary | Videotron | 29 |
+---------+---------+---------+-----------+
With a key on both sides, we can now execute an equi-join, and Spark can efficiently distribute the problem, resulting in optimal performance. However, in practice, this scenario is not realistic, as a genuine geolocation table often contains billions of rows.
To address this, we can enhance the efficiency by increasing the coarseness of this mapping. Instead of mapping IP ranges to each individual IP, we can map the IP ranges to segments within the IP space. Let’s assume we divide the IP space into segments of 5. The segmented space would look something like this:
+---------------+-------------+-----------+
| segment_start | segment_end | bucket_id |
+---------------+-------------+-----------+
| 1 | 5 | 0 |
| 6 | 10 | 1 |
| 11 | 15 | 2 |
| 16 | 20 | 3 |
| 21 | 25 | 4 |
| 26 | 30 | 5 |
+---------------+-------------+-----------+
Now, our objective is to map the IP ranges to the segments they overlap with. Similar to what we did earlier, we can unroll the IP ranges, but this time, we’ll do it in segments of 5.
SELECT
country,
city,
owner,
explode(sequence(start_ip / 5, end_ip / 5)) AS bucket_id
FROM
geolocations
We observe that certain IP ranges share a bucket_id. Ranges 1–2 and 3–4 both fall within the segment 1–5.
+----------+--------+---------+-----------+-----------+-----------+
| start_ip | end_ip | country | city | owner | bucket_id |
+----------+--------+---------+-----------+-----------+-----------+
| 1 | 2 | ca | Toronto | Telus | 0 |
| 3 | 4 | ca | Quebec | Rogers | 0 |
| 5 | 8 | ca | Vancouver | Bell | 1 |
| 10 | 14 | ca | Montreal | Telus | 2 |
| 19 | 22 | ca | Ottawa | Rogers | 3 |
| 19 | 22 | ca | Ottawa | Rogers | 4 |
| 23 | 29 | ca | Calgary | Videotron | 4 |
| 23 | 29 | ca | Calgary | Videotron | 5 |
+----------+--------+---------+-----------+-----------+-----------+
Additionally, we notice that some IP ranges are duplicated. The last two rows for the IP range 23–29 overlap with segments 20–25 and 26–30. Similar to the scenario where we unrolled individual IPs, we are still duplicating rows, but to a much lesser extent.
Now, we can utilize this bucketed table to perform our join.
SELECT
*
FROM
events
JOIN geolocation
ON (
event_ip / 5 = bucket_id
AND event_ip >= start_ip
AND event_ip <= end_ip
)
The equality in the join enables Spark to perform a Sort Merge Join (SMJ) strategy. The “between” condition eliminates cases where IP ranges share the same bucket_id.
In this illustration, we used segments of 5; however, in reality, we would segment the IP space into segments of 256. This is because the global IP address space is overseen by the Internet Assigned Numbers Authority (IANA), and traditionally, IANA allocates address space in blocks of 256 IPs.
Analyzing the IP ranges in a genuine geolocation table using the Spark approx_percentile function reveals that most records have spans of less than 256, while very few are larger than 256.
SELECT
approx_percentile(
end_ip - start_ip,
array(0.800, 0.900, 0.950, 0.990, 0.999, 0.9999),
10000)
FROM
geolocation
This implies that most IP ranges are assigned a bucket_id, while the few larger ones are unrolled, resulting in the unrolled table containing approximately an extra 10% of rows.
A query executed with a genuine geolocation table might resemble the following:
WITH
b_geo AS (
SELECT
explode(
sequence(
CAST(start_ip / 256 AS INT),
CAST(end_ip / 256 AS INT))) AS bucket_id,
*
FROM
geolocation
),
b_events AS (
SELECT
CAST(event_ip / 256 AS INT) AS bucket_id,
*
FROM
events
)
SELECT
*
FROM
b_events
JOIN b_geo
ON (
b_events.bucket_id = b_geo.bucket_id
AND b_events.event_ip >= b_geo.start_ip
AND b_events.event_ip <= b_geo.end_ip
);
In conclusion, this article has presented a practical demonstration of converting a non-equi join into an equi-join through the implementation of a mapping technique that involves segmenting IP ranges. It’s crucial to note that this approach extends beyond IP addresses and can be applied to any dataset characterized by bands or ranges.
The ability to effectively map and segment data is a valuable tool in the arsenal of data engineers and analysts, providing a pragmatic solution to the challenges posed by non-equality conditions in Spark SQL joins.
Performant IPv4 Range Spark Joins was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Performant IPv4 Range Spark Joins
Go Here to Read this Fast! Performant IPv4 Range Spark Joins

The image above is not just an appealing visual that drew you to this article (despite its length), but it also represents a potential journey of the SGD algorithm in search of a global minimum. In this journey, it navigates rocky paths where the height symbolizes the loss. If this doesn’t sound clear now, don’t worry, it will be by the end of this article.
Index:
· 1: Understanding the Basics
∘ 1.1: What is Gradient Descent
∘ 1.2: The ‘Stochastic’ in Stochastic Gradient Descent
· 2: The Mechanics of SGD
∘ 2.1: The Algorithm Explained
∘ 2.2: Understanding Learning Rate
· 3: SGD in Practice
∘ 3.1: Implementing SGD in Machine Learning Models
∘ 3.2: SGD in Sci-kit Learn and Tensorflow
· 4: Advantages and Challenges
∘ 4.1: Why Choose SGD?
∘ 4.2: Overcoming Challenges in SGD
· 5: Beyond Basic SGD
∘ 5.1: Variants of SGD
∘ 5.2: Future of SGD
· Conclusion

In machine learning , Gradient Descent is a star player. It’s an optimization algorithm used to minimize a function by iteratively moving towards the steepest descent as defined by the negative of the gradient. Like in the picture, imagine you’re at the top of a mountain, and your goal is to reach the lowest point. Gradient Descent helps you find the best path down the hill.
The beauty of Gradient Descent is its simplicity and elegance. Here’s how it works, you start with a random point on the function you’re trying to minimize, for example a random starting point on the mountain. Then, you calculate the gradient (slope) of the function at that point. In the mountain analogy, this is like looking around you to find the steepest slope. Once you know the direction, you take a step downhill in that direction, and then you calculate the gradient again. Repeat this process until you reach the bottom.
The size of each step is determined by the learning rate. However, if the learning rate is too small, it might take a long time to reach the bottom. If it’s too large, you might overshoot the lowest point. Finding the right balance is key to the success of the algorithm.
One of the most appealing aspects of Gradient Descent is its generality. It can be applied to almost any function, especially those where an analytical solution is not feasible. This makes it incredibly versatile in solving various types of problems in machine learning, from simple linear regression to complex neural networks.
Stochastic Gradient Descent (SGD) adds a twist to the traditional gradient descent approach. The term ‘stochastic’ refers to a system or process that is linked with a random probability. Therefore, this randomness is introduced in the way the gradient is calculated, which significantly alters its behavior and efficiency compared to standard gradient descent.
In traditional batch gradient descent, you calculate the gradient of the loss function with respect to the parameters for the entire training set. As you can imagine, for large datasets, this can be quite computationally intensive and time-consuming. This is where SGD comes into play. Instead of using the entire dataset to calculate the gradient, SGD randomly selects just one data point (or a few data points) to compute the gradient in each iteration.
Think of this process as if you were again descending a mountain, but this time in thick fog with limited visibility. Rather than viewing the entire landscape to decide your next step, you make your decision based on where your foot lands next. This step is small and random, but it’s repeated many times, each time adjusting your path slightly in response to the immediate terrain under your feet.
This stochastic nature of the algorithm provides several benefits:
However, the stochastic nature also introduces variability in the path to convergence. The algorithm doesn’t smoothly descend towards the minimum; rather, it takes a more zigzag path, which can sometimes make the convergence process appear erratic.
Stochastic Gradient Descent (SGD) might sound complex, but its algorithm is quite straightforward when broken down. Here’s a step-by-step guide to understanding how SGD works:
Initialization (Step 1)
First, you initialize the parameters (weights) of your model. This can be done randomly or by some other initialization technique. The starting point for SGD is crucial as it influences the path the algorithm will take.
Random Selection (Step 2)
In each iteration of the training process, SGD randomly selects a single data point (or a small batch of data points) from the entire dataset. This randomness is what makes it ‘stochastic’.
Compute the Gradient (Step 3)
Calculate the gradient of the loss function, but only for the randomly selected data point(s). The gradient is a vector that points in the direction of the steepest increase of the loss function. In the context of SGD, it tells you how to tweak the parameters to make the model more accurate for that particular data point.

Here, ∇θJ(θ) represents the gradient of the loss function J(θ) with respect to the parameters θ. This gradient is a vector of partial derivatives, where each component of the vector is the partial derivative of the loss function with respect to the corresponding parameter in θ.
Update the Parameters (Step 4)
Adjust the model parameters in the opposite direction of the gradient. Here’s where the learning rate η plays a crucial role. The formula for updating each parameter is:

where:
The learning rate determines the size of the steps you take towards the minimum. If it’s too small, the algorithm will be slow; if it’s too large, you might overshoot the minimum.
Repeat until convergence (Step 5)
Repeat steps 2 to 4 for a set number of iterations or until the model performance stops improving. Each iteration provides a slightly updated model.
Ideally, after many iterations, SGD converges to a set of parameters that minimize the loss function, although due to its stochastic nature, the path to convergence is not as smooth and may oscillate around the minimum.
One of the most crucial hyperparameters in the Stochastic Gradient Descent (SGD) algorithm is the learning rate. This parameter can significantly impact the performance and convergence of the model. Understanding and choosing the right learning rate is a vital step in effectively employing SGD.
What is Learning Rate?
At this point you should have an idea of what learning rate is, but let’s better define it for clarity. The learning rate in SGD determines the size of the steps the algorithm takes towards the minimum of the loss function. It’s a scalar that scales the gradient, dictating how much the weights in the model should be adjusted during each update. If you visualize the loss function as a valley, the learning rate decides how big a step you take with each iteration as you walk down the valley.
Too High Learning Rate
If the learning rate is too high, the steps taken might be too large. This can lead to overshooting the minimum, causing the algorithm to diverge or oscillate wildly without finding a stable point.
Think of it as taking leaps in the valley and possibly jumping over the lowest point back and forth.
Too Low Learning Rate
On the other hand, a very low learning rate leads to extremely small steps. While this might sound safe, it significantly slows down the convergence process.
In a worst-case scenario, the algorithm might get stuck in a local minimum or even stop improving before reaching the minimum.
Imagine moving so slowly down the valley that you either get stuck or it takes an impractically long time to reach the bottom.
Finding the Right Balance
The ideal learning rate is neither too high nor too low but strikes a balance, allowing the algorithm to converge efficiently to the global minimum.
Typically, the learning rate is chosen through experimentation and is often set to decrease over time. This approach is called learning rate annealing or scheduling.
Learning Rate Scheduling
Learning rate scheduling involves adjusting the learning rate over time. Common strategies include:
Link to the full code (Jupyter Notebook): https://github.com/cristianleoo/models-from-scratch-python/blob/main/sgd.ipynb
Implementing Stochastic Gradient Descent (SGD) in machine learning models is a practical step that brings the theoretical aspects of the algorithm into real-world application. This section will guide you through the basic implementation of SGD and provide tips for integrating it into machine learning workflows.
Now let’s consider a simple case of SGD applied to Linear Regression:
class SGDRegressor:
def __init__(self, learning_rate=0.01, epochs=100, batch_size=1, reg=None, reg_param=0.0):
"""
Constructor for the SGDRegressor.
Parameters:
learning_rate (float): The step size used in each update.
epochs (int): Number of passes over the training dataset.
batch_size (int): Number of samples to be used in each batch.
reg (str): Type of regularization ('l1' or 'l2'); None if no regularization.
reg_param (float): Regularization parameter.
The weights and bias are initialized as None and will be set during the fit method.
"""
self.learning_rate = learning_rate
self.epochs = epochs
self.batch_size = batch_size
self.reg = reg
self.reg_param = reg_param
self.weights = None
self.bias = None
def fit(self, X, y):
"""
Fits the SGDRegressor to the training data.
Parameters:
X (numpy.ndarray): Training data, shape (m_samples, n_features).
y (numpy.ndarray): Target values, shape (m_samples,).
This method initializes the weights and bias, and then updates them over a number of epochs.
"""
m, n = X.shape # m is number of samples, n is number of features
self.weights = np.zeros(n)
self.bias = 0
for _ in range(self.epochs):
indices = np.random.permutation(m)
X_shuffled = X[indices]
y_shuffled = y[indices]
for i in range(0, m, self.batch_size):
X_batch = X_shuffled[i:i+self.batch_size]
y_batch = y_shuffled[i:i+self.batch_size]
gradient_w = -2 * np.dot(X_batch.T, (y_batch - np.dot(X_batch, self.weights) - self.bias)) / self.batch_size
gradient_b = -2 * np.sum(y_batch - np.dot(X_batch, self.weights) - self.bias) / self.batch_size
if self.reg == 'l1':
gradient_w += self.reg_param * np.sign(self.weights)
elif self.reg == 'l2':
gradient_w += self.reg_param * self.weights
self.weights -= self.learning_rate * gradient_w
self.bias -= self.learning_rate * gradient_b
def predict(self, X):
"""
Predicts the target values using the linear model.
Parameters:
X (numpy.ndarray): Data for which to predict target values.
Returns:
numpy.ndarray: Predicted target values.
"""
return np.dot(X, self.weights) + self.bias
def compute_loss(self, X, y):
"""
Computes the loss of the model.
Parameters:
X (numpy.ndarray): The input data.
y (numpy.ndarray): The true target values.
Returns:
float: The computed loss value.
"""
return (np.mean((y - self.predict(X)) ** 2) + self._get_regularization_loss()) ** 0.5
def _get_regularization_loss(self):
"""
Computes the regularization loss based on the regularization type.
Returns:
float: The regularization loss.
"""
if self.reg == 'l1':
return self.reg_param * np.sum(np.abs(self.weights))
elif self.reg == 'l2':
return self.reg_param * np.sum(self.weights ** 2)
else:
return 0
def get_weights(self):
"""
Returns the weights of the model.
Returns:
numpy.ndarray: The weights of the linear model.
"""
return self.weights
Let’s break it down into smaller steps:
Initialization (Step 1)
def __init__(self, learning_rate=0.01, epochs=100, batch_size=1, reg=None, reg_param=0.0):
self.learning_rate = learning_rate
self.epochs = epochs
self.batch_size = batch_size
self.reg = reg
self.reg_param = reg_param
self.weights = None
self.bias = None
The constructor (__init__ method) initializes the SGDRegressor with several parameters:
Fit the Model(Step 2)
def fit(self, X, y):
m, n = X.shape # m is number of samples, n is number of features
self.weights = np.zeros(n)
self.bias = 0
for _ in range(self.epochs):
indices = np.random.permutation(m)
X_shuffled = X[indices]
y_shuffled = y[indices]
for i in range(0, m, self.batch_size):
X_batch = X_shuffled[i:i+self.batch_size]
y_batch = y_shuffled[i:i+self.batch_size]
gradient_w = -2 * np.dot(X_batch.T, (y_batch - np.dot(X_batch, self.weights) - self.bias)) / self.batch_size
gradient_b = -2 * np.sum(y_batch - np.dot(X_batch, self.weights) - self.bias) / self.batch_size
if self.reg == 'l1':
gradient_w += self.reg_param * np.sign(self.weights)
elif self.reg == 'l2':
gradient_w += self.reg_param * self.weights
self.weights -= self.learning_rate * gradient_w
self.bias -= self.learning_rate * gradient_b
This method fits the model to the training data. It starts by initializing weights as a zero vector of length n (number of features) and bias to zero. The model’s parameters are updated over a number of epochs through SGD.
Random Selection and Batches(Step 3)
for _ in range(self.epochs):
indices = np.random.permutation(m)
X_shuffled = X[indices]
y_shuffled = y[indices]
In each epoch, the data is shuffled, and batches are created to update the model parameters using SGD.
Compute the Gradient and Update the parameters (Step 4)
gradient_w = -2 * np.dot(X_batch.T, (y_batch - np.dot(X_batch, self.weights) - self.bias)) / self.batch_size
gradient_b = -2 * np.sum(y_batch - np.dot(X_batch, self.weights) - self.bias) / self.batch_size
Gradients for weights and bias are computed in each batch. These are then used to update the model’s weights and bias. If regularization is used, it’s also included in the gradient calculation.
Repeat and converge (Step 5)
def predict(self, X):
return np.dot(X, self.weights) + self.bias
The predict method calculates the predicted target values using the learned linear model.
Compute Loss (Step 6)
def compute_loss(self, X, y):
return (np.mean((y - self.predict(X)) ** 2) + self._get_regularization_loss()) ** 0.5
It calculates the mean squared error between the predicted values and the actual target values y. Additionally, it incorporates the regularization loss if regularization is specified.
Regularization Loss Calculation (Step 7)
def _get_regularization_loss(self):
if self.reg == 'l1':
return self.reg_param * np.sum(np.abs(self.weights))
elif self.reg == 'l2':
return self.reg_param * np.sum(self.weights ** 2)
else:
return 0
This private method computes the regularization loss based on the type of regularization (l1 or l2) and the regularization parameter. This loss is added to the main loss function to penalize large weights, thereby avoiding overfitting.
Now, while the code above is very useful for educational purposes, data scientists definitely don’t use it on a daily basis. Indeed, we can directly call SGD with few lines of code from popular libraries such as scikit learn (machine learning) or tensorflow (deep learning).
SGD for linear regression in scikit-learn
from sklearn.linear_model import SGDRegressor
# Create and fit the model
model = SGDRegressor(max_iter=1000)
model.fit(X, y)
# Making predictions
predictions = model.predict(X)
SGD regressor is directly called from sklearn library, and follows the same structure of other algorithms in the same library.
The parameter ‘max_iter’ is the number of epochs (rounds). By specifying max_iter to 1000 we will make the algorithm update the linear regression weights and bias 1000 times.
Neural Network with SGD optimization in Tensorflow
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
# Create a simple neural network model
model = Sequential([
Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
Dense(1)
])
sgd = SGD(learning_rate=0.01)
# Compile the model with SGD optimizer
model.compile(optimizer=sgd, loss='categorical_crossentropy', metrics=['accuracy'])
# Train the model
model.fit(X, y, epochs=10)
In this code we are defining a Neural Network with one Dense Layer and 64 nodes. However, besides the specifics of the neural network, here we are again calling SGD with just two lines of code:
from tensorflow.keras.optimizers import SGD
sgd = SGD(learning_rate=0.01)
Efficiency with Large Datasets:
Scalability: One of the primary advantages of SGD is its efficiency in handling large-scale data. Since it updates parameters using only a single data point (or a small batch) at a time, it is much less memory-intensive than algorithms requiring the entire dataset for each update.
Speed: By frequently updating the model parameters, SGD can converge more quickly to a good solution, especially in cases where the dataset is enormous.
Flexibility and Adaptability:
Online Learning: SGD’s ability to update the model incrementally makes it well-suited for online learning, where the model needs to adapt continuously as new data arrives.
Handling Non-Static Datasets: For datasets that change over time, SGD’s incremental update approach can adjust to these changes more effectively than batch methods.
Overcoming Challenges of Local Minima:
The stochastic nature of SGD helps it to potentially escape local minima, a significant challenge in many optimization problems. The random fluctuations allow the algorithm to explore a broader range of the solution space.
General Applicability:
SGD can be applied to a wide range of problems and is not limited to specific types of models. This general applicability makes it a versatile tool in the machine learning toolbox.
Simplicity and Ease of Implementation:
Despite its effectiveness, SGD remains relatively simple to understand and implement. This ease of use is particularly appealing for those new to machine learning.
Improved Generalization:
By updating the model frequently with a high degree of variance, SGD can often lead to models that generalize better on unseen data. This is because the algorithm is less likely to overfit to the noise in the training data.
Compatibility with Advanced Techniques:
SGD is compatible with a variety of enhancements and extensions, such as momentum, learning rate scheduling, and adaptive learning rate methods like Adam, which further improve its performance and versatility.
While Stochastic Gradient Descent (SGD) is a powerful and versatile optimization algorithm, it comes with its own set of challenges. Understanding these hurdles and knowing how to overcome them can greatly enhance the performance and reliability of SGD in practical applications.
Choosing the Right Learning Rate
Selecting an appropriate learning rate is crucial for SGD. If it’s too high, the algorithm may diverge; if it’s too low, it might take too long to converge or get stuck in local minima.
Use a learning rate schedule or adaptive learning rate methods. Techniques like learning rate annealing, where the learning rate decreases over time, can help strike the right balance.
Dealing with Noisy Updates
The stochastic nature of SGD leads to noisy updates, which can cause the algorithm to be less stable and take longer to converge.
Implement mini-batch SGD, where the gradient is computed on a small subset of the data rather than a single data point. This approach can reduce the variance in the updates.
Risk of Local Minima and Saddle Points
In complex models, SGD can get stuck in local minima or saddle points, especially in high-dimensional spaces.
Use techniques like momentum or Nesterov accelerated gradients to help the algorithm navigate through flat regions and escape local minima.
Sensitivity to Feature Scaling
SGD is sensitive to the scale of the features, and having features on different scales can make the optimization process inefficient.
Normalize or standardize the input features so that they are on a similar scale. This practice can significantly improve the performance of SGD.
Hyperparameter Tuning
SGD requires careful tuning of hyperparameters, not just the learning rate but also parameters like momentum and the size of the mini-batch.
Utilize grid search, random search, or more advanced methods like Bayesian optimization to find the optimal set of hyperparameters.
Overfitting
Like any machine learning algorithm, there’s a risk of overfitting, where the model performs well on training data but poorly on unseen data.
Use regularization techniques such as L1 or L2 regularization, and validate the model using a hold-out set or cross-validation.
Stochastic Gradient Descent (SGD) has several variants, each designed to address specific challenges or to improve upon the basic SGD algorithm in certain aspects. These variants enhance SGD’s efficiency, stability, and convergence rate. Here’s a look at some of the key variants:
Mini-Batch Gradient Descent
This is a blend of batch gradient descent and stochastic gradient descent. Instead of using the entire dataset (as in batch GD) or a single sample (as in SGD), it uses a mini-batch of samples.
It reduces the variance of the parameter updates, which can lead to more stable convergence. It can also take advantage of optimized matrix operations, which makes it more computationally efficient.
Momentum SGD
Momentum is an approach that helps accelerate SGD in the relevant direction and dampens oscillations. It does this by adding a fraction of the previous update vector to the current update.
It helps in faster convergence and reduces oscillations. It is particularly useful for navigating the ravines of the cost function, where the surface curves much more steeply in one dimension than in another.
Nesterov Accelerated Gradient (NAG)
A variant of momentum SGD, Nesterov momentum is a technique that makes a more informed update by calculating the gradient of the future approximate position of the parameters.
It can speed up convergence and improve the performance of the algorithm, particularly in the context of convex functions.
Adaptive Gradient (Adagrad)
Adagrad adapts the learning rate to each parameter, giving parameters that are updated more frequently a lower learning rate.
It’s particularly useful for dealing with sparse data and is well-suited for problems where data is scarce or features have very different frequencies.
RMSprop
RMSprop (Root Mean Square Propagation) modifies Adagrad to address its radically diminishing learning rates. It uses a moving average of squared gradients to normalize the gradient.
It works well in online and non-stationary settings and has been found to be an effective and practical optimization algorithm for neural networks.
Adam (Adaptive Moment Estimation)
Adam combines ideas from both Momentum and RMSprop. It computes adaptive learning rates for each parameter.
Adam is often considered as a default optimizer due to its effectiveness in a wide range of applications. It’s particularly good at solving problems with noisy or sparse gradients.
Each of these variants has its own strengths and is suited for specific types of problems. Their development reflects the ongoing effort in the machine learning community to refine and enhance optimization algorithms to achieve better and faster results. Understanding these variants and their appropriate applications is crucial for anyone looking to delve deeper into machine learning optimization techniques.
As we delve into the future of Stochastic Gradient Descent (SGD), it’s clear that this algorithm continues to evolve, reflecting the dynamic and innovative nature of the field of machine learning. The ongoing research and development in SGD focus on enhancing its efficiency, accuracy, and applicability to a broader range of problems. Here are some key areas where we can expect to see significant advancements:
Automated Hyperparameter Tuning
There’s increasing interest in automating the process of selecting optimal hyperparameters, including the learning rate, batch size, and other SGD-specific parameters.
This automation could significantly reduce the time and expertise required to effectively deploy SGD, making it more accessible and efficient.
Integration with Advanced Models
As machine learning models become more complex, especially with the growth of deep learning, there’s a need to adapt and optimize SGD for these advanced architectures.
Enhanced versions of SGD that are tailored for complex models can lead to faster training times and improved model performance.
Adapting to Non-Convex Problems
Research is focusing on making SGD more effective for non-convex optimization problems, which are prevalent in real-world applications.
Improved strategies for dealing with non-convex landscapes could lead to more robust and reliable models in areas like natural language processing and computer vision.
Decentralized and Distributed SGD
With the increase in distributed computing and the need for privacy-preserving methods, there’s a push towards decentralized SGD algorithms that can operate over networks.
This approach can lead to more scalable and privacy-conscious machine learning solutions, particularly important for big data applications.
Quantum SGD
The advent of quantum computing presents an opportunity to explore quantum versions of SGD, leveraging quantum algorithms for optimization.
Quantum SGD has the potential to dramatically speed up the training process for certain types of models, though this is still largely in the research phase.
SGD in Reinforcement Learning and Beyond
Adapting and applying SGD in areas like reinforcement learning, where the optimization landscapes are different from traditional supervised learning tasks.
This could open new avenues in developing more efficient and powerful reinforcement learning algorithms.
Ethical and Responsible AI
There’s a growing awareness of the ethical implications of AI models, including those trained using SGD.
Research into SGD might also focus on ensuring that models are fair, transparent, and responsible, aligning with broader societal values.
As we wrap up our exploration of Stochastic Gradient Descent (SGD), it’s clear that this algorithm is much more than just a method for optimizing machine learning models. It stands as a testament to the ingenuity and continuous evolution in the field of artificial intelligence. From its basic form to its more advanced variants, SGD remains a critical tool in the machine learning toolkit, adaptable to a wide array of challenges and applications.
If you liked the article please leave a clap, and let me know in the comments what you think about it!
Stochastic Gradient Descent: Math and Python Code was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Stochastic Gradient Descent: Math and Python Code
Go Here to Read this Fast! Stochastic Gradient Descent: Math and Python Code



If you, like me, ventured into the world of data science (be it through college or one of the countless online courses), you may have harbored the dream of creating an ML/AI software product that people can use. A product just like those our CS friends seem to code up effortlessly.
But if you ever tried your hand at full-stack web development, you’d soon face the seemingly insurmountable hurdles of configuration, deployment, terminal commands and servers and so on.

I know this all too well, having spent countless hours floundering helplessly, which only deepened my inferiority complex that I’d never manage to craft a functioning software app.
But exactly one year ago, on the 21st of January, a weekend unexpectedly made free by passport-troubles and a cancelled trip, I embarked on a journey to make an AI app. It was a journey that led me to unexpected places — teaming up with a co-founder halfway across the world, joining a San Francisco startup accelerator, and eventually growing to thousands of users with a significant annual revenue (check out my app, Podsmart! we summarize podcasts).
But most importantly, it was a journey full of frustrations, backtracking, mistakes and rework. It was about navigating the bewildering world of software development without a formal CS/SWE background.
So, looking back at the past year building my first software product, I’ve compiled a guide of some technical tips — this is for any data science enthusiast who wants to build a functional web app serving thousands of users.
This guide is born from my struggles and learnings over a year, and represents advice I would have loved to tell my one-year-younger self.
Disclaimer: These tips are from my specific personal experiences, and may work differently for others. I also do not have any relationship or affiliation with any of the tools recommended here.
· What you want to build
· The dangers of YouTube web development tutorials
∘ Tip #1: Use Next.js instead of React
∘ Tip #2: Opt for Tailwind CSS instead of Bootstrap for styling
· The trappings of the data science mindset
∘ Tip #3: Choose FastAPI over Flask for your backend, and rigorously define response models
∘ Tip #4: Use TypeScript instead of JavaScript
· About deployment…
∘ Tip #5: Use Modal for GPU backend
∘ Tip #6: Use AWS Lambda for backend deployment and Vercel for frontend
· Making life easier
∘ Tip #7: don’t build your own landing page using React
∘ Tip #8: Firebase + Stripe for user authentication and payments
∘ Tip #9: Implement Sentry for error monitoring
· Conclusion
To build said functional web app, you need a web interface (frontend or client) for users to interact with, as well as a server (backend) which does data processing, data storage, and calling the ML/AI models.
(You might have heard of Streamlit. It’s great for the simplest demos, but it really lacks the customizability to make a viable production app)
As a data scientist, many aspects of software development fill me with trepidation, such as the prospect of wasting days on broken configuration. Nothing is more frustrating than seeing something break and not know why it broke and how to fix it.
As a result, I relied desperately on walkthrough-style tutorials, especially on YouTube, that depicted the entire process, from start to end, of setting up a React project, deploying a backend or website etc.
Looking back, there are two main downsides to this:
Firstly, confusion at multiple conflicting and potentially outdated tutorials (for instance, as newer versions of React come out). This has often led to me following a tutorial until realizing it no longer works.
Secondly, most tutorials are aimed at building cool classroom demos which are beginner-friendly. Hence, they use frameworks and reinforce coding patterns which have a low performance ceiling, which will be lacking for production and scaling. On hindsight, I’ve picked up many bad coding habits from YouTube tutorials, that are now obstacles to further developing my app as a live product serving thousands of users.
Since you learn best from failures, this process, though frustrating, was a massive learning experience for me throughout the year. Hopefully you can save lots of time learning from my failures.

Many YouTube tutorials advocate for React, and I initially followed suit.
However, eventually I wanted to improve my site’s SEO performance — which is crucial to gaining more users. React’s limitations, such as inability to change meta tags dynamically, and lack of server-side rendering, were frustrating, necessitating a tedious change to Next.js. After switching, the differences in performance were just night-and-day.

Some people say React is more beginner-friendly, but there are lots of Next.js templates online, for example by Vercel (Next.js creators), especially AI applications. Next.js is really the modern web framework used for nearly every AI application.
Embarking on my front-end UI journey, I initially, and somewhat naively, followed the herd of frontend tutorials, towards Bootstrap. Its allure? The promise of ease with ready-made components like dropdowns and accordions.

However, after a while, I realized that my website just looked … really ugly, especially when compared to the sleek, modern AI demo pages out there. There was this unmistakable ‘Bootstrap look’ — a sort of aesthetic stubbornness that resisted customization, entangled in a web of confusingly named CSS classes. So eventually, I once again bit the bullet and redid my entire frontend with Tailwind CSS, taking 3 whole days.
If you’ve ever seen an AI demo page with a modern and clean UI, it’s highly likely they used Tailwind CSS.

Initially, I was intimidated by Tailwind — its long component definitions brimming with what seemed like cryptic utility classes appeared anything but beginner-friendly… I thought that Tailwind lacked pre-built components and it would be onerous to memorize the utility classes. However, this couldn’t be more untrue! There are many great UI component libraries built on Tailwind CSS — I used Flowbite React (it has all the components I need!)
As a data science student, I’ve grown to love Python with its minimalist, powerful code syntax. Python’s type-inference spared me the tedium of defining types for every variable (a task I found cumbersome, especially in languages I encountered in intro CS classes like Java).
Hence, I used JavaScript for my frontend and Python for my backend, avoiding defining the types of my API endpoints unless necessary.
However, as my app grew in complexity, tons of unexpected type errors between my frontend and backend eroded my coding productivity. I’m finally understanding my CS friends’ insistence on the importance of explicit types. It turns out, the meticulous detail in type definition isn’t just pedantic — it’s essential.
If you search for Python backend tutorials on YouTube, most videos would point you to Flask. Just like how a broken clock is right twice a day, I somehow happened to choose FastAPI as my Python backend, which was definitely correct decision on hindsight.
(Though hilariously, I had totally disregarded the benefit of FastAPI. Until only recently, I didn’t understand the need to define Pydantic classes for POST requests and thought it more of a hassle than a help.)
FastAPI has several game-changing benefits:

But the most important thing is FastAPI’s type annotations.
This ensures that each route has outputs of a consistent data structure. But to unleash the full power of this feature, we need to…
For the longest time, I’ve manually written my frontend fetcher methods (once again learning from full-stack tutorials), hence adding new routes to my app was a long and error-prone process.
You can hence imagine my shock when my big-tech SWE friend told me that you can auto-generate Typescript client code using your API specification. (see here for more FastAPI’s documentation, one such package is openapi-typescript-codegen)

In an instant, I realized that this would solve two major challenges simultaneously: removing my manual and error-prone client fetcher writing, and ensuring type consistency between my backend and frontend. This significantly reduced the persistent type errors that were undermining my app’s reliability.
Of course, having type constraints for your backend routes only helps if your frontend enforces those type constraints — which naturally requires TypeScript.
Hence, I’m currently undergoing the arduous process of defining response models for my FastAPI backend, and converting my frontend from JavaScript to TypeScript, a process that you can avoid if you start with FastAPI and TypeScript from the start!
Through my data science / ML classes, I’ve grown used to hopping onto Google Colab, pressing play, and voila, the code runs. So, it’s no surprise that the very thought of deployment fills me with dread. But as the founder of the Buildspace accelerator puts it, you need to “GTFOL” (Get The F Off Localhost) to make your software apps accessible to the world. Hence, I naturally wanted the deployment to be as painless as possible.
If you want to deploy your own models (e.g. ML models, image recognition, Whisper for transcription, or more recently, open-source LLMs like Llama), you will need a GPU cloud provider to host your model.
My advice is to choose Modal and never look back.
Modal stands out with its superb documentation and learning resources, complete with up-to-date sample code for the latest applications — from fine-tuning open-source LLMs to serving LLM chatbots, and more.
I actually started my entire podcast-transcribing app forking Modal’s sample audio-transcription code, and so it isn’t an exaggeration to say that without Modal I wouldn’t have built my app.

Modal shines in its user-friendliness (and coming from someone who loathes deployment, that’s saying a lot). Just write cloud functions on my local code editor, and deploy it using one terminal command. Its dashboard is so user-friendly (especially compared to AWS), allowing me to track my app’s usage, analyze performance, and trace errors very easily.
Last of all, Modal serves as my escape valve when it comes to functionality that Lambda doesn’t have, or is tedious to implement, e.g. file storage (this will come in useful in the next point…) and scheduling functions.
When hosting my Python backend, I was confused over whether to use Amazon EC2 or AWS Lambda. My app requires the storage of audio files (which could get big), and since Lambda’s serverless architecture isn’t meant to store files (it had 2 GB of ephemeral storage, but it isn’t persistent), I had thought I had to use Amazon EC2. However, EC2 was much more cumbersome to configure, and being an always-on dedicated instance, it would be much more expensive and difficult to scale.
This is where Modal’s free file storage came into the rescue, and I was able to structure my backend to be compatible with Lambda, while downloading and storing files when needed on Modal.
Thankfully, this video was really good, and following their instructions exactly enabled me to successfully deploy my backend.
For my frontend, Vercel was all I needed. The process was hassle-free and, aside from domain name costs, entirely free.
The last 3 miscellaneous tips that would save you from wasting massive amounts of time in development…
Yet another mistake I did because all those full-stack tutorials fooled me into thinking I had to code my own landing page with React. Sure, you can (and I did), but there’s a low ceiling of performance and aesthetics — precisely the important traits you need for a successful landing page.
React is only better for custom functionality like the actual AI app interface. For the landing page with purely static content, you should instead, use no-code site builders like Webflow or Framer to rapidly build landing pages (and outsource landing page creation to your designer so you can work on other things!)
When it comes to user authentication, the number of options and tutorials out there can once again be overwhelming. I needed a solution that not only handled authentication but also integrated with a payment system to control access based on user subscription status.
After spending days trying and failing to use several different authentication solutions e.g. auth0, I found that Stripe + Firebase worked well. Firebase has a Stripe integration that updates users’ subscription status upon successful payment, and Firebase’s React client does client-side authentication, and Python client does server access control well. Following these two videos (here and here) enabled me to successfully implement this on my app.
For months, I had no clue what bugs users encountered with my app in production. Only when myself or a user spots a bug, do I comb through AWS Cloudwatch interface to try to find the backend bug.

This continued until my co-founder introduced me to Sentry, a tool for performance monitoring and error tracking of cloud apps. It’s really easy to initialize for your frontend and backend, and you can even integrate it with Slack to get instant error notifications. Just be careful not to deplete your free plan’s monthly error budget on a trivial but frequent error like authentication timeout. That’s what happened to me — and I had to subscribe to the paid plan to find logs for the important bugs I actually wanted to solve.
Bonus Tip #10: don’t try to build a web app using Spotify’s API! I wasted my app for 2 months assuming I could integrate Spotify’s API to allow users to load their saved podcasts. But to productionize this, you need to apply for a quota extension request, which takes more than a month for Spotify to review. And they’ll probably reject the application anyway if your app involves any AI/ML model (despite my app not actually using Spotify data to train any model, the wording that is prohibited in their Developer Policy).
Thank you for reading this technical guide! I hope this guide demystifies some aspects of web app development for fellow data science enthusiasts.
If you found this post helpful, let me know in the comments what other topics related to data science and AI you’d like me to explore!
Lastly, I’d love for you to check out my app — Podsmart transcribes and summarizes podcasts and YouTube videos to help you discover knowledge from the audio medium, saving busy intellectuals hours of listening. We’re expanding our team and looking for frontend and backend developers, reach out if you’re interested.
From Data Scientist to AI Developer: Lessons Building an Generative AI Web App in 2023 was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
From Data Scientist to AI Developer: Lessons Building an Generative AI Web App in 2023
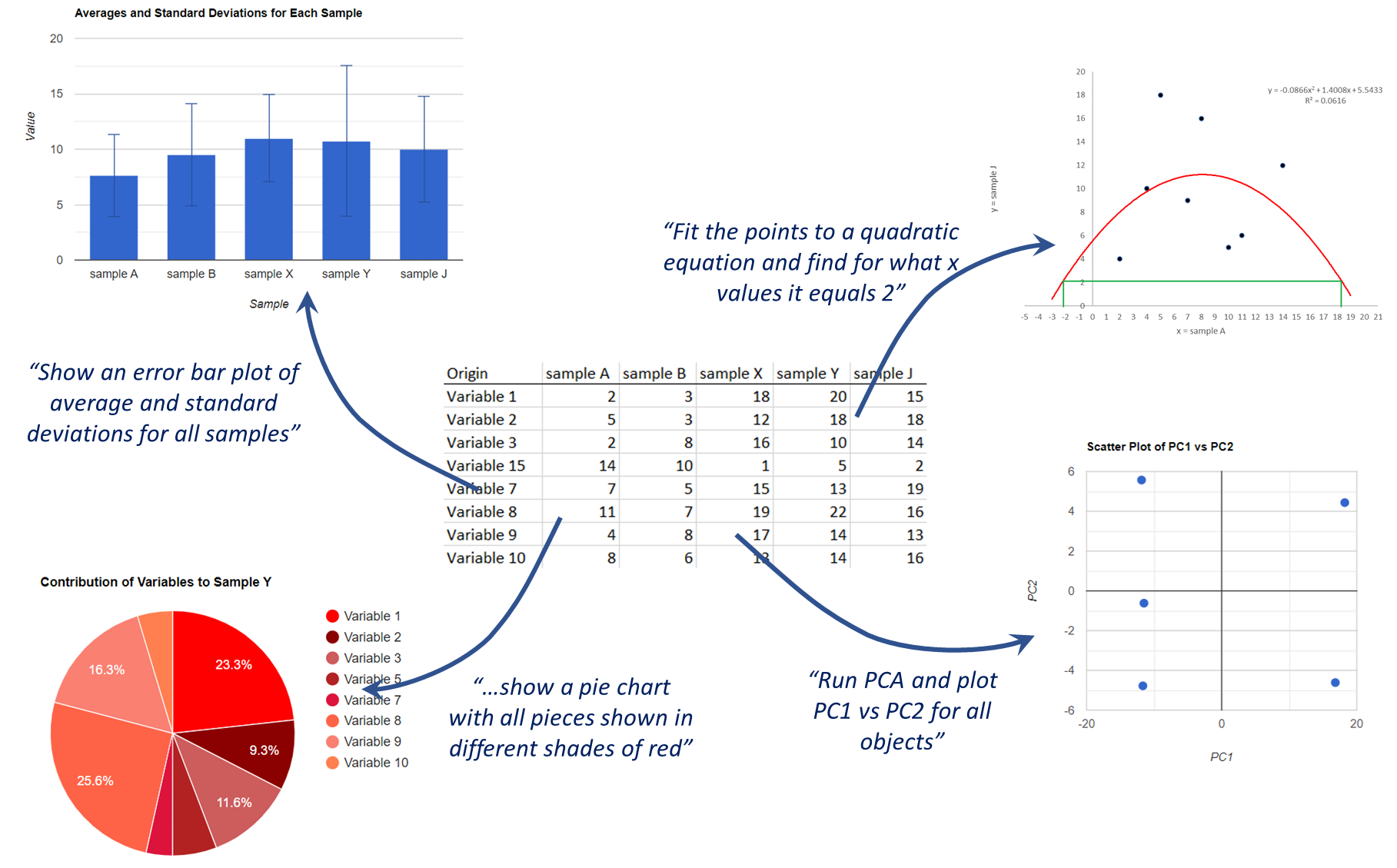
LucianoSphere (Luciano Abriata, PhD)
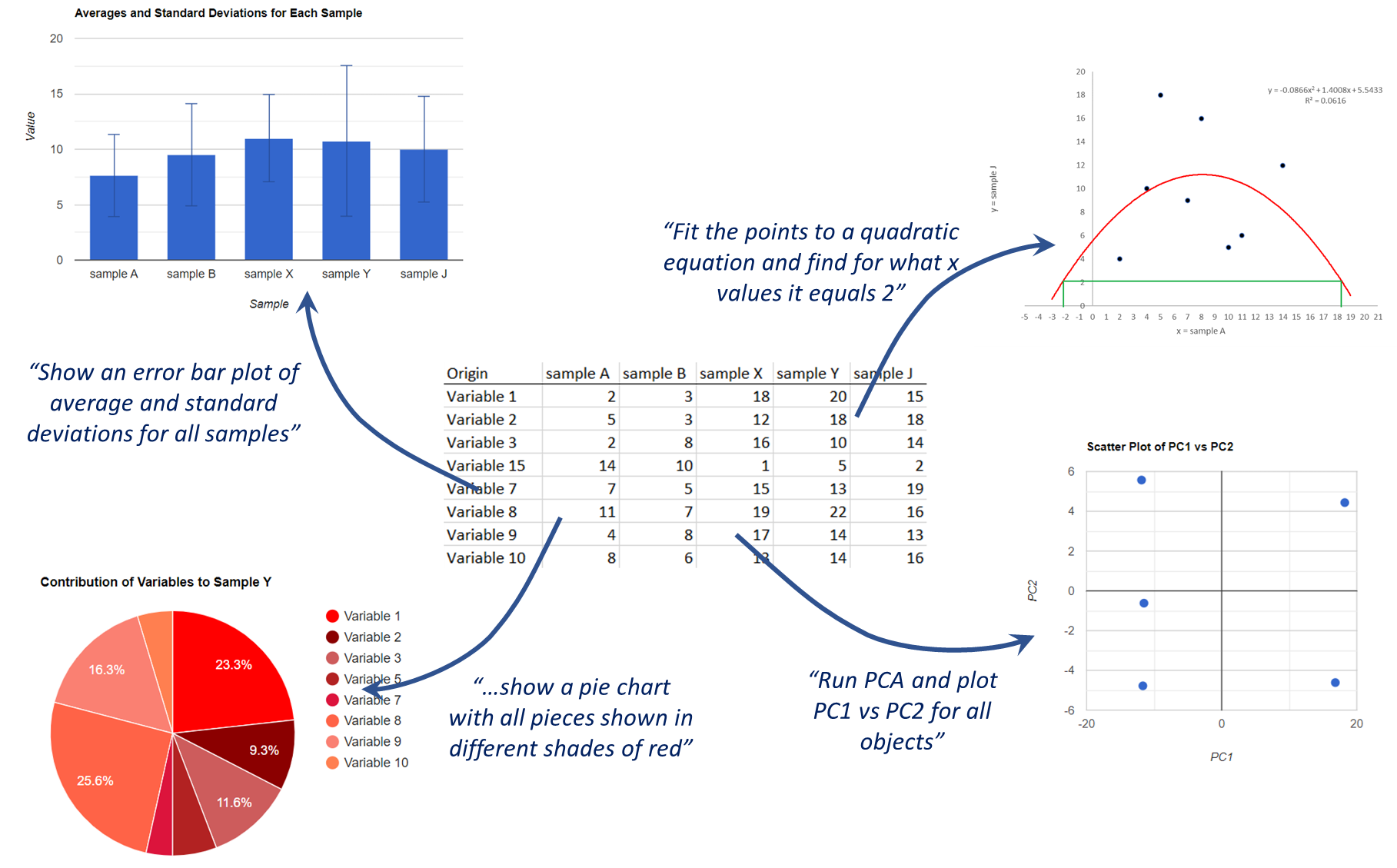
Getting LLMs to analyze and plot data for you, right in your web browser
Originally appeared here:
Powerful Data Analysis and Plotting via Natural Language Requests by Giving LLMs Access to…
Discover the concepts and basic methods of causal machine learning applied in Python
Originally appeared here:
Introduction to Causal Inference with Machine Learning in Python
Go Here to Read this Fast! Introduction to Causal Inference with Machine Learning in Python
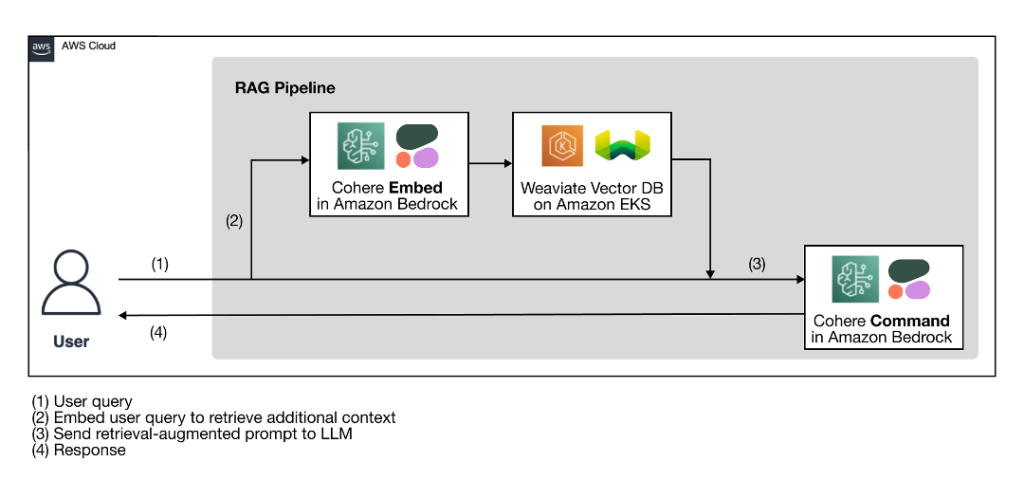
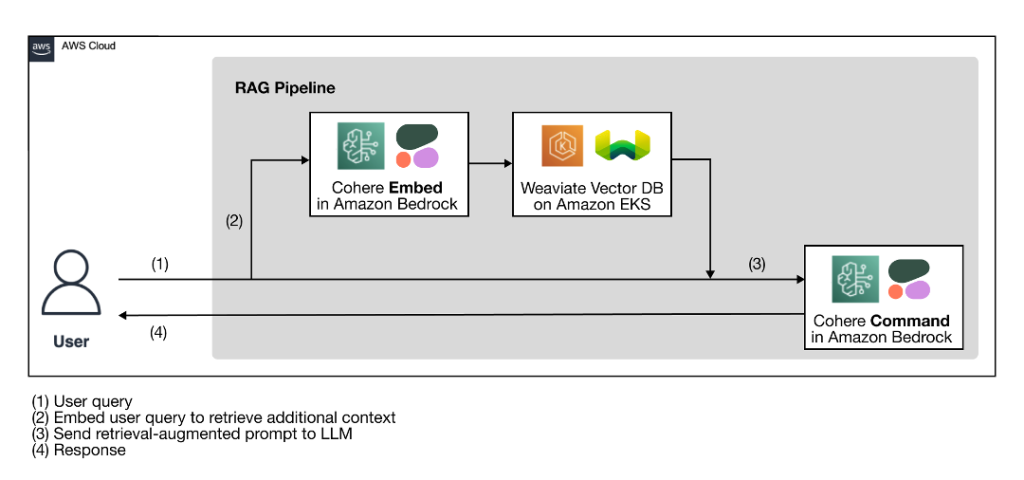
Originally appeared here:
Build enterprise-ready generative AI solutions with Cohere foundation models in Amazon Bedrock and Weaviate vector database on AWS Marketplace