
Originally appeared here:
Build private and secure enterprise generative AI applications with Amazon Q Business using IAM Federation
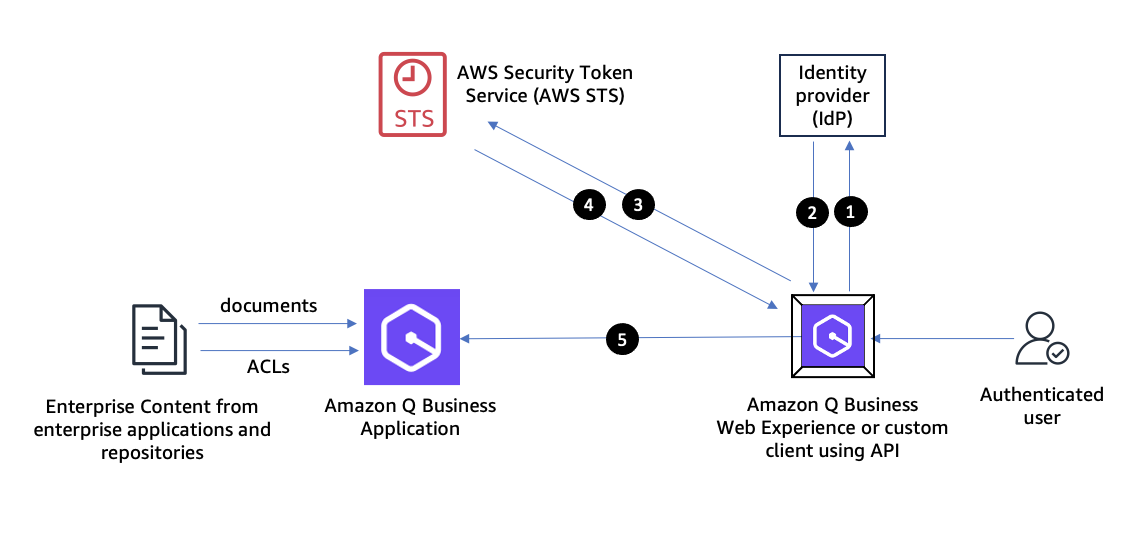

Originally appeared here:
Build private and secure enterprise generative AI applications with Amazon Q Business using IAM Federation
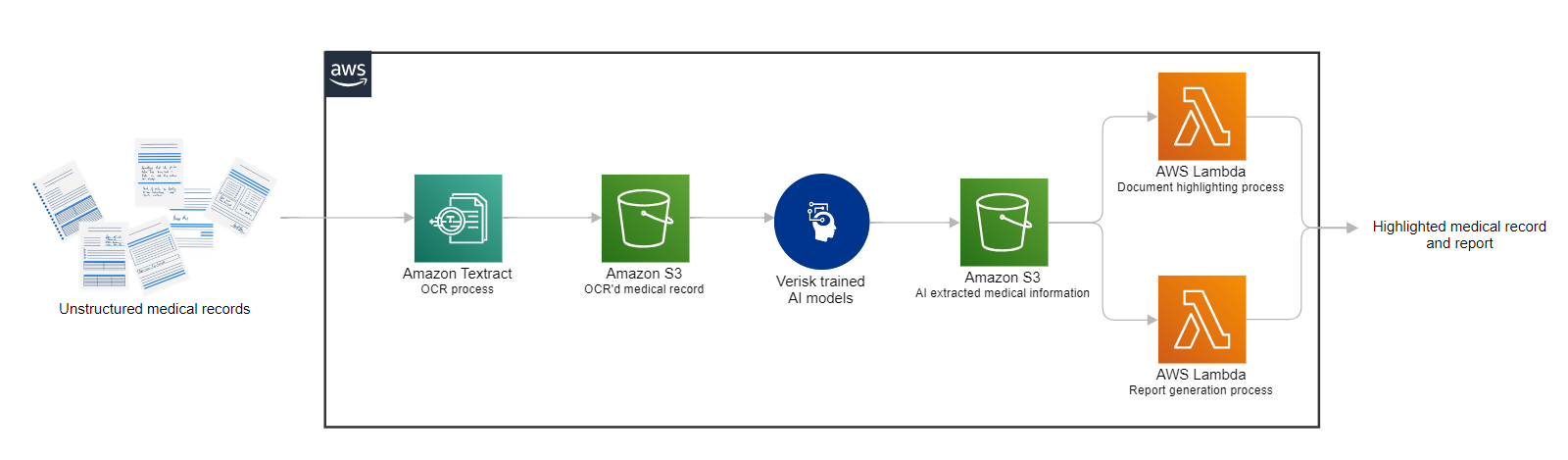

Originally appeared here:
Unleashing the power of generative AI: Verisk’s Discovery Navigator revolutionizes medical record review



Reinforcement learning is a domain in machine learning that introduces the concept of an agent learning optimal strategies in complex environments. The agent learns from its actions, which result in rewards, based on the environment’s state. Reinforcement learning is a challenging topic and differs significantly from other areas of machine learning.
What is remarkable about reinforcement learning is that the same algorithms can be used to enable the agent adapt to completely different, unknown, and complex conditions.
Note. To fully understand the concepts included in this article, it is highly recommended to be familiar with concepts discussed in previous articles.
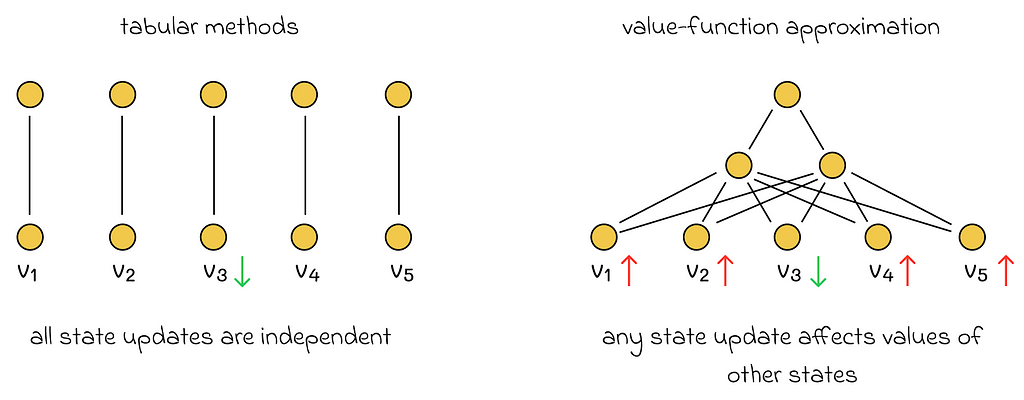
Up until now, we have only been discussing tabular reinforcement learning methods. In this context, the word “tabular” indicates that all possible actions and states can be listed. Therefore, the value function V or Q is represented in the form of a table, while the ultimate goal of our algorithms was to find that value function and use it to derive an optimal policy.
However, there are two major problems regarding tabular methods that we need to address. We will first look at them and then introduce a novel approach to overcome these obstacles.
This article is based on Chapter 9 of the book “Reinforcement Learning” written by Richard S. Sutton and Andrew G. Barto. I highly appreciate the efforts of the authors who contributed to the publication of this book.
The first aspect that has to be clear is that tabular methods are only applicable to problems with a small number of states and actions. Let us recall a blackjack example where we applied the Monte Carlo method in part 3. Despite the fact that there were only 200 states and 2 actions, we got good approximations only after executing several million episodes!
Imagine what colossal computations we would need to perform if we had a more complex problem. For example, if we were dealing with RGB images of size 128 × 128, then the total number of states would be 3 ⋅ 256 ⋅ 256 ⋅ 128 ⋅ 128 ≈ 274 billion. Even with modern technological advancements, it would be absolutely impossible to perform the necessary computations to find the value function!
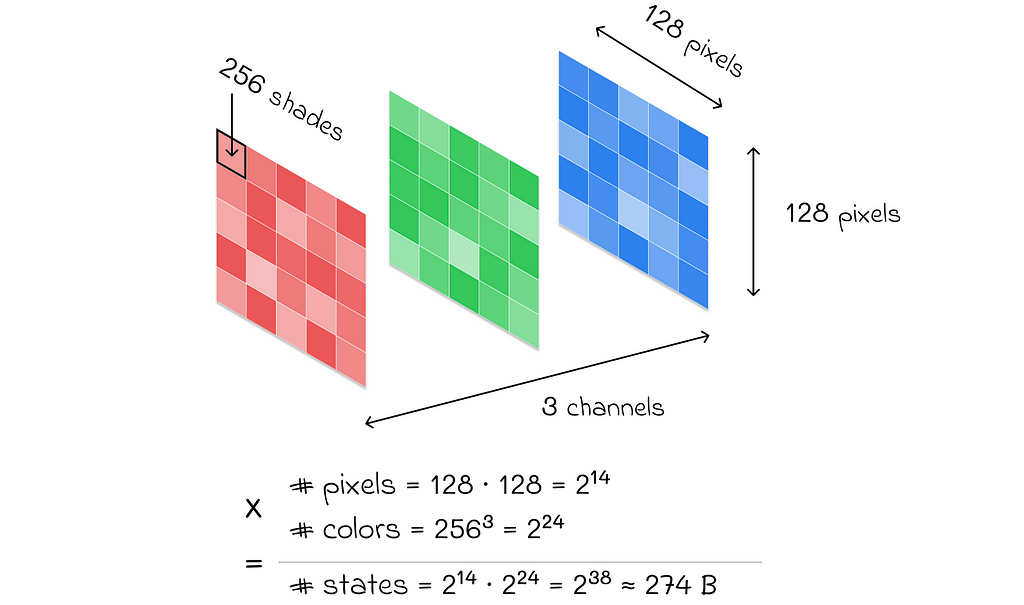
In reality, most environments in reinforcement learning problems have a huge number of states and possible actions that can be taken. Consequently, value function estimation with tabular methods is no longer applicable.
Even if we imagine that there are no problems regarding computations, we are still likely to encounter states that are never visited by the agent. How can standard tabular methods evaluate v- or q-values for such states?
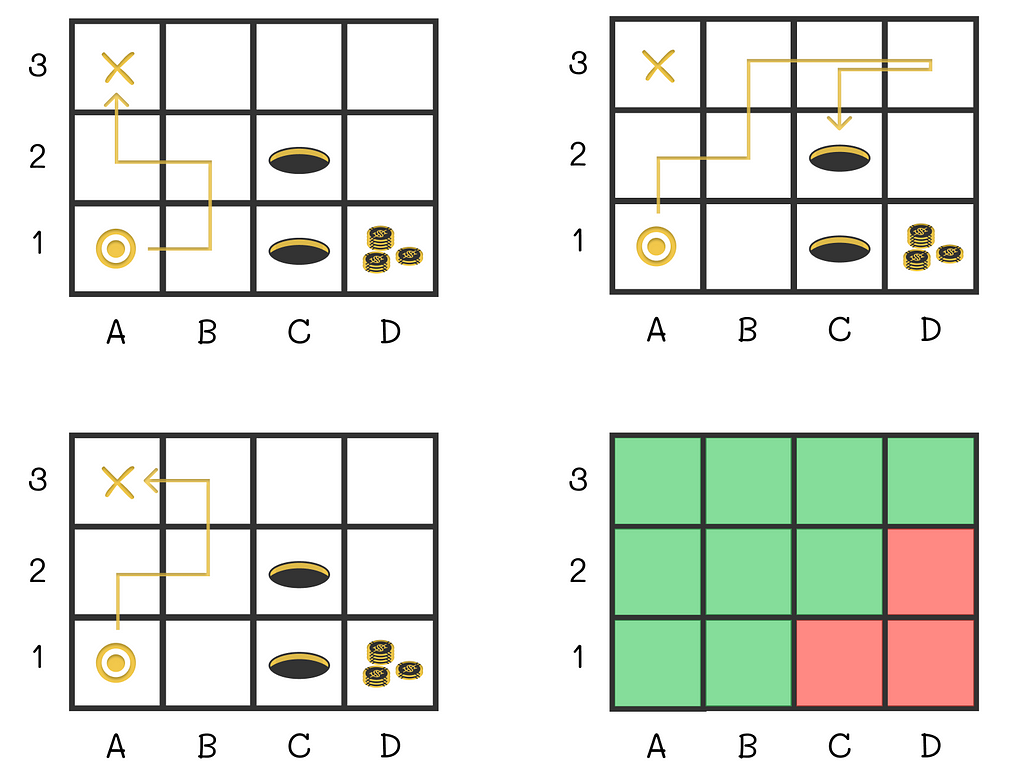
This article will propose a novel approach based on supervised learning that will efficiently approximate value functions regardless the number of states and actions.
The idea of value-function approximation lies in using a parameterized vector w that can approximate a value function. Therefore, from now on, we will write the value function v̂ as a function of two arguments: state s and vector w:
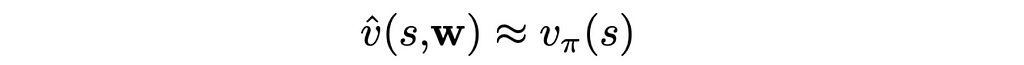
Our objective is to find v̂ and w. The function v̂ can take various forms but the most common approach is to use a supervised learning algorithm. As it turns out, v̂ can be a linear regression, decision tree, or even a neural network. At the same time, any state s can be represented as a set of features describing this state. These features serve as an input for the algorithm v̂.
Why are supervised learning algorithms used for v̂?
It is known that supervised learning algorithms are very good at generalization. In other words, if a subset (X₁, y₁) of a given dataset D for training, then the model is expected to also perform well for unseen examples X₂.
At the same time, we highlighted above the generalization problem for reinforcement learning algorithms. In this scenario, if we apply a supervised learning algorithm, then we should no longer worry about generalization: even if a model has not seen a state, it would still try to generate a good approximate value for it using available features of the state.
Let us return to the maze and show an example of how the value function can look. We will represent the current state of the agent by a vector consisting of two components:
For v, we can use the scalar product of s and w. Assuming that the agent is currently located at cell B1, the value function v̂ will take the form shown in the image below:
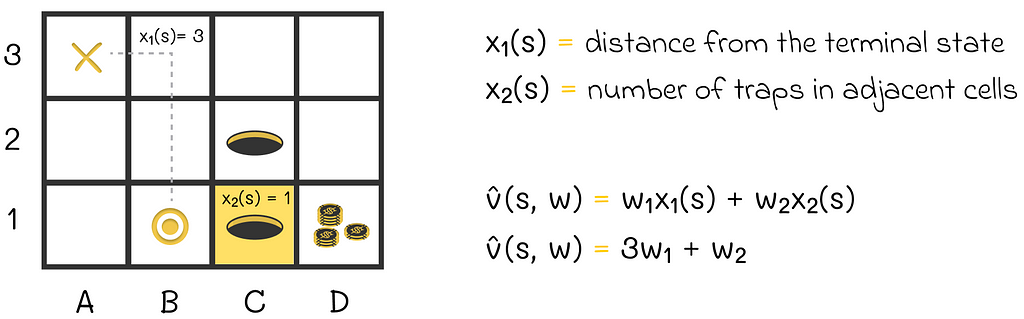
With the presented idea of supervised learning, there are two principal difficulties we have to address:
1. Learned state values are no longer decoupled. In all previous algorithms we discussed, an update of a single state did not affect any other states. However, now state values depend on vector w. If the vector w is updated during the learning process, then it will change the values of all other states. Therefore, if w is adjusted to improve the estimate of the current state, then it is likely that estimations of other states will become worse.
2. Supervised learning algorithms require targets for training that are not available. We want a supervised algorithm to learn the mapping between states and true value functions. The problem is that we do not have any true state values. In this case, it is not even clear how to calculate a loss function.
We cannot completely get rid of the first problem, but what we can do is to specify how much each state is important to us. This can be done by creating a state distribution that maps every state to its importance weight.
This information can then be taken into account in the loss function.
Most of the time, μ(s) is chosen proportionally to how often state s is visited by the agent.
Assuming that v̂(s, w) is differentiable, we are free to choose any loss function we like. Throughout this article, we will be looking at the example of the MSE (mean squared error). Apart from that, to account for the state distribution μ(s), every error term is scaled by its corresponding weight:
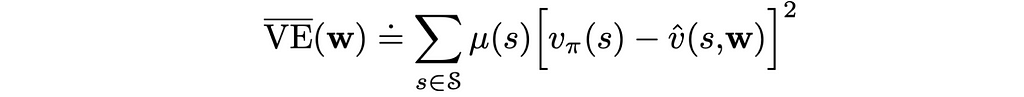
In the shown formula, we do not know the true state values v(s). Nevertheless, we will be able to overcome this issue in the next section.
After having defined the loss function, our ultimate goal becomes to find the best vector w that will minimize the objective VE(w). Ideally, we would like to converge to the global optimum, but in reality, the most complex algorithms can guarantee convergence only to a local optimum. In other words, they can find the best vector w* only in some neighbourhood of w.
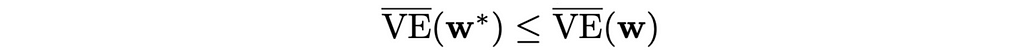
Despite this fact, in many practical cases, convergence to a local optimum is often enough.
Stochastic-gradient methods are among the most popular methods to perform function approximation in reinforcement learning.
Let us assume that on iteration t, we run the algorithm through a single state example. If we denote by wₜ a weight vector at step t, then using the MSE loss function defined above, we can derive the update rule:
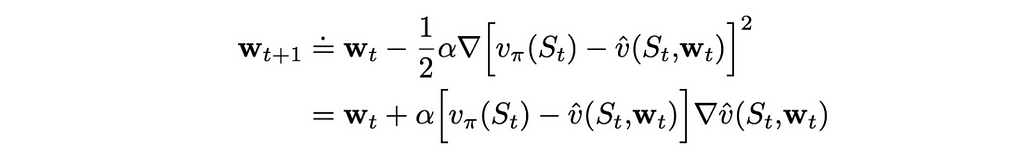
We know how to update the weight vector w but what can we use as a target in the formula above? First of all, we will change the notation a little bit. Since we cannot obtain exact true values, instead of v(S), we are going to use another letter U, which will indicate that true state values are approximated.
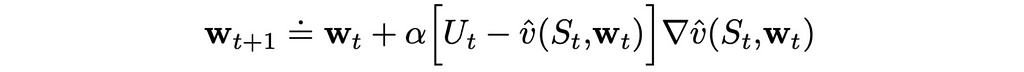
The ways the state values can be approximated are discussed in the following sections.
Monte Carlo is the simplest method that can be used to approximate true values. What makes it great is that the state values computed by Monte Carlo are unbiased! In other words, if we run the Monte Carlo algorithm for a given environment an infinite number of times, then the averaged computed state values will converge to the true state values:
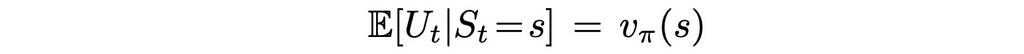
Why do we care about unbiased estimations? According to theory, if target values are unbiased, then SGD is guaranteed to converge to a local optimum (under appropriate learning rate conditions).
In this way, we can derive the Gradient Monte Carlo algorithm, which uses expected returns Gₜ as values for Uₜ:

Once the whole episode is generated, all expected returns are computed for every state included in the episode. The respective expected returns are used during the weight vector w update. For the next episode, new expected returns will be calculated and used for the update.
As in the original Monte Carlo method, to perform an update, we have to wait until the end of the episode, and that can be a problem in some situations. To overcome this disadvantage, we have to explore other methods.
At first sight, bootstrapping seems like a natural alternative to gradient Monte Carlo. In this version, every target is calculated using the transition reward R and the target value of the next state (or n steps later in the general case):
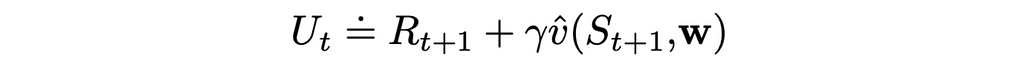
However, there are still several difficulties that need to be addressed:
The good news is that both of these problems can be overcome with semi-gradient methods.
Despite losing important convergence guarantees, it turns out that using bootstrapping under certain constraints on the value function (discussed in the next section) can still lead to good results.
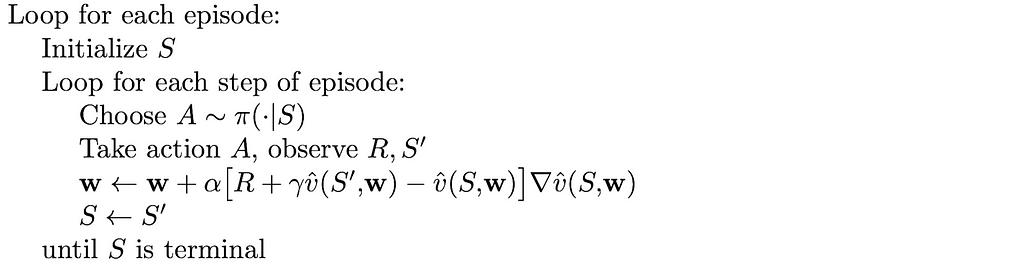
As we have already seen in part 5, compared to Monte Carlo methods, bootstrapping offers faster learning, enabling it to be online and is usually preferred in practice. Logically, these advantages also hold for gradient methods.
Let us look at a particular case where the value function is a scalar product of the weight vector w and the feature vector x(s):
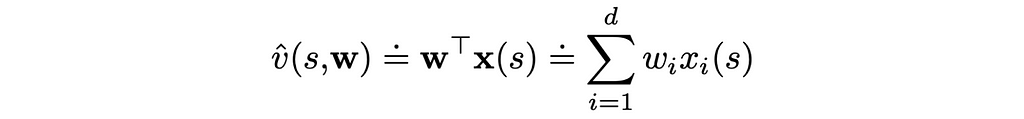
This is the simplest form the value function can take. Furthermore, the gradient of the scalar product is just the feature vector itself:
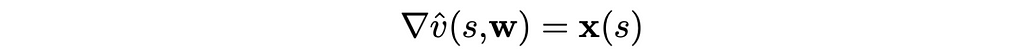
As a result, the update rule for this case is extremely simple:
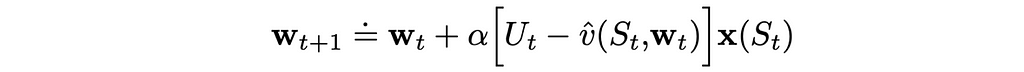
The choice of the linear function is particularly attractive because, from the mathematical point of view, value approximation problems become much easier to analyze.
Instead of the SGD algorithm, it is also possible to use the method of least squares.
The choice of the linear function makes the optimization problem convex. Therefore, there is only one optimum.
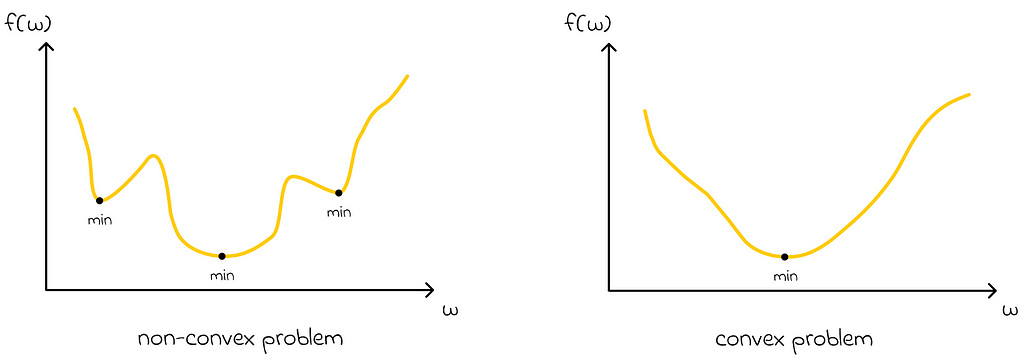
In this case, regarding gradient Monte Carlo (if its learning rate α is adjusted appropriately), an important conclusion can be made:
Since the gradient Monte Carlo method is guaranteed to converge to a local optimum, it is automatically guaranteed that the found local optimum will be global when using the linear value approximation function.
According to theory, under the linear value function, gradient one-step TD algorithms also converge. The only subtlety is that the convergence point (which is called the TD fixed point) is usually located near the global optimum. Despite this, the approximation quality with the TD fixed point if often enough in most tasks.
In this article, we have understood the scalability limitations of standard tabular algorithms. This led us to the exploration of value-function approximation methods. They allow us to view the problem from a slightly different angle, which elegantly transforms the reinforcement learning problem into a supervised machine learning task.
The previous knowledge of Monte Carlo and bootstrapping methods helped us elaborate their respective gradient versions. While gradient Monte Carlo comes with stronger theoretical guarantees, bootstrapping (especially the one-step TD algorithm) is still a preferred method due to its faster convergence.
All images unless otherwise noted are by the author.
Reinforcement Learning, Part 7: Introduction to Value-Function Approximation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Reinforcement Learning, Part 7: Introduction to Value-Function Approximation
How to implement semantic chunking and gain better results.
Originally appeared here:
Why Does Position-Based Chunking Lead to Poor Performance in RAGs?
Go Here to Read this Fast! Why Does Position-Based Chunking Lead to Poor Performance in RAGs?
Retrieval Augmented Generation (RAG) has dominated the discussion around making Gen AI applications useful since ChatGPT’s advent exploded the AI hype. The idea is simple. LLMs become especially useful once we connect them to our private data. A foundational model, that everyone has access to, combined with our domain-specific data as the secret sauce results in a potent, unique tool. Just like in the human world, AI systems seem to develop into an economy of experts. General knowledge is a useful base, but expert knowledge will work out your AI system’s unique selling proposition.
Recap: RAG itself does not yet describe any specific architecture or method. It only depicts the augmentation of a given generation task with an arbitrary retrieval method. The original RAG paper (Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks by Lewis et. al.) compares a two-tower embedding approach with bag-of-words retrieval.
Text Embedding-based retrieval has been described in many occurrences. It already allows our LLM application to answer questions based on the content of a given knowledge base extremely reliably. The core strength of Text2Vec retrieval remains: Extracting a given fact represented in the embedded knowledge base and formulating an answer to the user query that is grounded using that extracted fact. However, text embedding search also comes with major challenges. Usually, every text embedding represents one specific chunk from the unstructured dataset. The nearest neighbor search finds embeddings that represent chunks semantically similar to the incoming user query. That also means the search is semantic but still highly specific. Thus candidate quality is highly dependent on query quality. Furthermore, embeddings represent the content mentioned in your knowledge base. This does not represent cases in which you are looking to answer questions that require an abstraction across documents or concepts within a document in your knowledge base.
For example, imagine a knowledge base containing the bios of all past Nobel Peace Prize winners. Asking the Text2Vec-RAG system “Who won the Nobel Peace Prize 2023?” would be an easy question to answer. This fact is well represented in the embedded document chunks. Thus the final answer can be grounded in the correct context. On the other hand, the RAG system might struggle by asking “Who were the most notable Nobel Peace Prize winners of the last decade?”. We might be successful after adding more context such as “Who were the most notable Nobel Peace Prize winners fighting against the Middle East conflict?”, but even that will be a difficult one to solve solely based on text embeddings (given the current quality of embedding models). Another example is whole dataset reasoning. For example, your user might be interested in asking your LLM application “What are the top 3 topics that recent Nobel Peace Prize winners stood up for?”. Embedded chunks do not allow reasoning across documents. Our nearest neighbor search is looking for a specific mention of “the top 3 topics that recent Nobel Peace Prize winners stood up for” in the knowledge base. If this is not included in the knowledge base, any purely text-embedding-based LLM application will struggle and most likely fail to answer this question correctly and especially exhaustively.
We need an alternative retrieval method that allows us to answer these “Global”, aggregative questions in addition to the “Local” extractive questions. Welcome to Graph RAG!
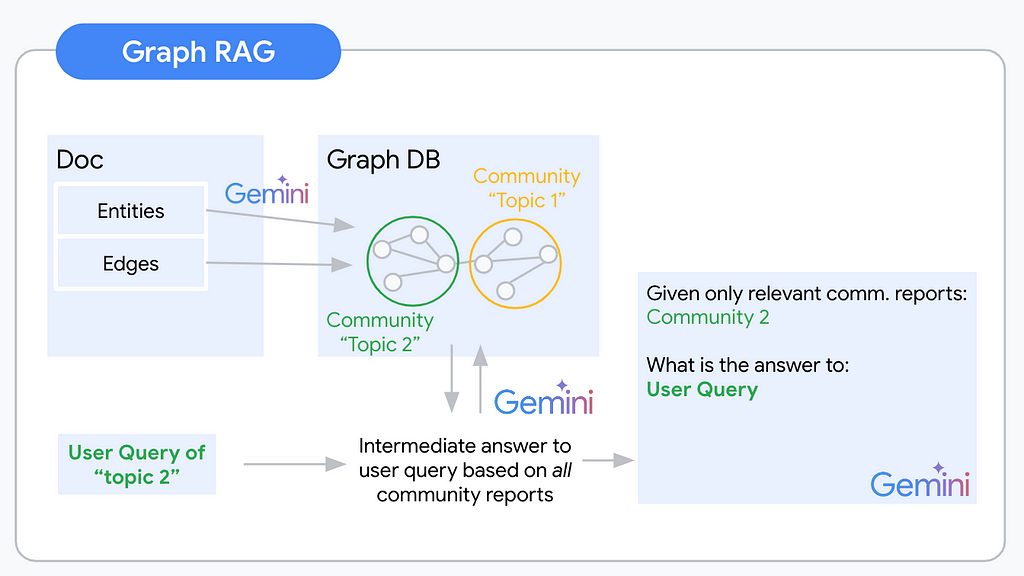
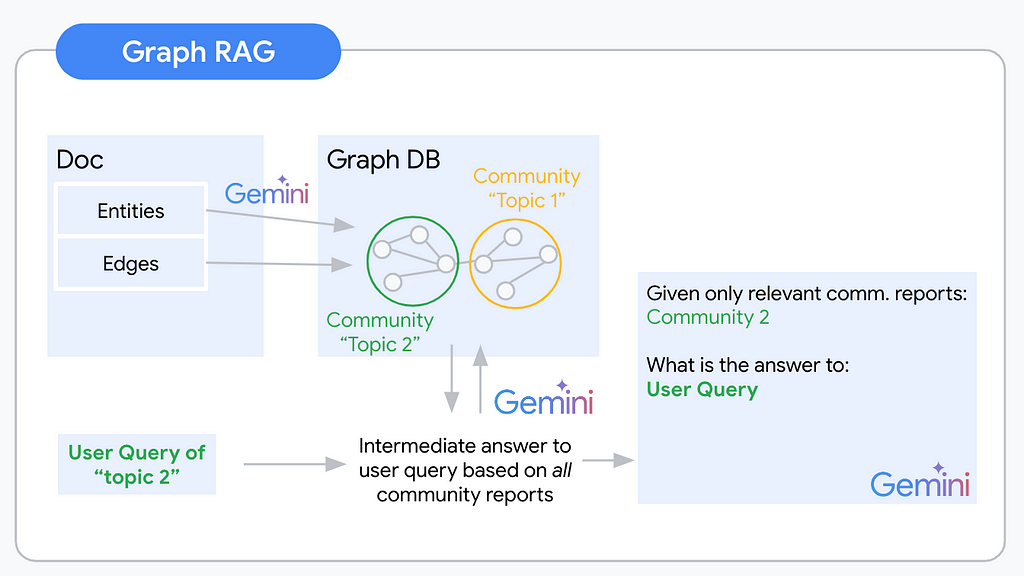
Knowledge Graphs are a semi-structured, hierarchical approach to organizing information. Once information is organized as a graph we can infer information about specific nodes, but also their relationships and neighbors. The graph structure allows reasoning on a global dataset level because nodes and the connections between them can span across documents. Given this graph, we can also analyze neighboring nodes and communities of nodes that are more tightly connected within each other than they are to other nodes. A community of nodes can be expected to roughly cover one topic of interest. Abstracting across the community nodes and their connections can give us an abstract understanding of concepts within this topic. Graph RAG uses this understanding of communities within a knowledge graph to propose context for a given user query.
A Graph RAG pipeline will usually follow the following steps:

The process of building abstracted understanding for our unstructured knowledge base begins with extracting the nodes and edges that will build your knowledge graph. You automate this extraction via an LLM. The biggest challenge of this step is deciding which concepts and relationships are relevant to include. To give an example for this highly ambiguous task: Imagine you are extracting a knowledge graph from a document about Warren Buffet. You could extract his holdings, place of birth, and many other facts as entities with respective edges. Most likely these will be highly relevant information for your users. (With the right document) you could also extract the color of his tie at the last board meeting. This will (most likely) be irrelevant to your users. It is crucial to specify the extraction prompt to the application use case and domain. This is because the prompt will determine what information is extracted from the unstructured data. For example, if you are interested in extracting information about people, you will need to use a different prompt than if you are interested in extracting information about companies.
The easiest way to specify the extraction prompt is via multishot prompting. This involves giving the LLM multiple examples of the desired input and output. For instance, you could give the LLM a series of documents about people and ask it to extract the name, age, and occupation of each person. The LLM would then learn to extract this information from new documents. A more advanced way to specify the extraction prompt is through LLM fine-tuning. This involves training the LLM on a dataset of examples of the desired input and output. This can cause better performance than multishot prompting, but it is also more time-consuming.
Here is the Microsoft graphrag extraction prompt.
You designed a solid extraction prompt and tuned your LLM. Your extraction pipeline works. Next, you will have to think about storing these results. Graph databases (DB) such as Neo4j and Arango DB are the straightforward choice. However, extending your tech stack by another db type and learning a new query language (e.g. Cypher/Gremlin) can be time-consuming. From my high-level research, there are also no great serverless options available. If handling the complexity of most Graph DBs was not enough, this last one is a killer for a serverless lover like myself. There are alternatives though. With a little creativity for the right data model, graph data can be formatted as semi-structured, even strictly structured data. To get you inspired I coded up graph2nosql as an easy Python interface to store and access your graph dataset in your favorite NoSQL db.
The data model defines a format for Nodes, Edges, and Communities. Store all three in separate collections. Every node, edge, and community finally identify via a unique identifier (UID). Graph2nosql then implements a couple of essential operations needed when working with knowledge graphs such as adding/removing nodes/edges, visualizing the graph, detecting communities, and more.

Once the graph is extracted and stored, the next step is to identify communities within the graph. Communities are clusters of nodes that are more tightly connected than they are to other nodes in the graph. This can be done using various community detection algorithms.
One popular community detection algorithm is the Louvain algorithm. The Louvain algorithm works by iteratively merging nodes into communities until a certain stopping criterion is met. The stopping criterion is typically based on the modularity of the graph. Modularity is a measure of how well the graph is divided into communities.
Other popular community detection algorithms include:
Now use the resulting communities as a base to generate your community reports. Community reports are summaries of the nodes and edges within each community. These reports can be used to understand graph structure and identify key topics and concepts within the knowledge base. In a knowledge graph, every community can be understood to represent one “topic”. Thus every community might be a useful context to answer a different type of questions.
Aside from summarizing multiple nodes’ information, community reports are the first abstraction level across concepts and documents. One community can span over the nodes added by multiple documents. That way you’re building a “global” understanding of the indexed knowledge base. For example, from your Nobel Peace Prize winner dataset, you probably extracted a community that represents all nodes of the type “Person” that are connected to the node “Nobel Peace prize” with the edge description “winner”.
A great idea from the Microsoft Graph RAG implementation are “findings”. On top of the general community summary, these findings are more detailed insights about the community. For example, for the community containing all past Nobel Peace Prize winners, one finding could be some of the topics that connected most of their activism.
Just as with graph extraction, community report generation quality will be highly dependent on the level of domain and use case adaptation. To create more accurate community reports, use multishot prompting or LLM fine-tuning.
Here the Microsoft graphrag community report generation prompt.
At query time you use a map-reduce pattern to first generate intermediate responses and a final response.
In the map step, you combine every community-userquery pair and generate an answer to the user query using the given community report. In addition to this intermediate response to the user question, you ask the LLM to evaluate the relevance of the given community report as context for the user query.
In the reduce step you then order the relevance scores of the generated intermediate responses. The top k relevance scores represent the communities of interest to answer the user query. The respective community reports, potentially combined with the node and edge information are the context for your final LLM prompt.
Text2vec RAG leaves obvious gaps when it comes to knowledge base Q&A tasks. Graph RAG can close these gaps and it can do so well! The additional abstraction layer via community report generation adds significant insights into your knowledge base and builds a global understanding of its semantic content. This will save teams an immense amount of time screening documents for specific pieces of information. If you are building an LLM application it will enable your users to ask the big questions that matter. Your LLM application will suddenly be able to seemingly think around the corner and understand what is going on in your user’s data instead of “only” quoting from it.
On the other hand, a Graph RAG pipeline (in its raw form as described here) requires significantly more LLM calls than a text2vec RAG pipeline. Especially the generation of community reports and intermediate answers are potential weak points that are going to cost a lot in terms of dollars and latency.
As so often in search you can expect the industry around advanced RAG systems to move towards a hybrid approach. Using the right tool for a specific query will be essential when it comes to scaling up RAG applications. A classification layer to separate incoming local and global queries could for example be imaginable. Maybe the community report and findings generation is enough and adding these reports as abstracted knowledge into your index as context candidates suffices.
Luckily the perfect RAG pipeline is not solved yet and your experiments will be part of the solution. I would love to hear about how that is going for you!
Graph RAG — A conceptual introduction was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Graph RAG — A conceptual introduction
Go Here to Read this Fast! Graph RAG — A conceptual introduction

Originally appeared here:
Index your Atlassian Confluence Cloud contents using the Amazon Q Confluence Cloud connector for Amazon Q Business
You have probably seen or interacted with a graph whether you realize it or not. Our world is composed of relationships. Who we know, how we interact, how we transact — graphs structure information in a way that makes these inherent relationships explicit.
Analytically speaking, knowledge graphs provide the most intuitive means to synthesize and represent connections within and across datasets for analysis. A knowledge graph is a technical artifact “that presents data visually as entities and the relationships between them.” It gives an analyst a digital model of a problem. And it looks something like this…

This article discusses what makes a great graph and answers some common questions pertaining to their technical implementation.
Graphs can represent almost anything where there is interaction or exchange. Entities (or nodes) can be people, companies, documents, geographic locations, bank accounts, crypto wallets, physical assets, etc. Edges (or links) can represent conversations, phone calls, e-mails, academic citations, network packet transfer, ad impressions and conversions, financial transactions, personal relationships, etc.
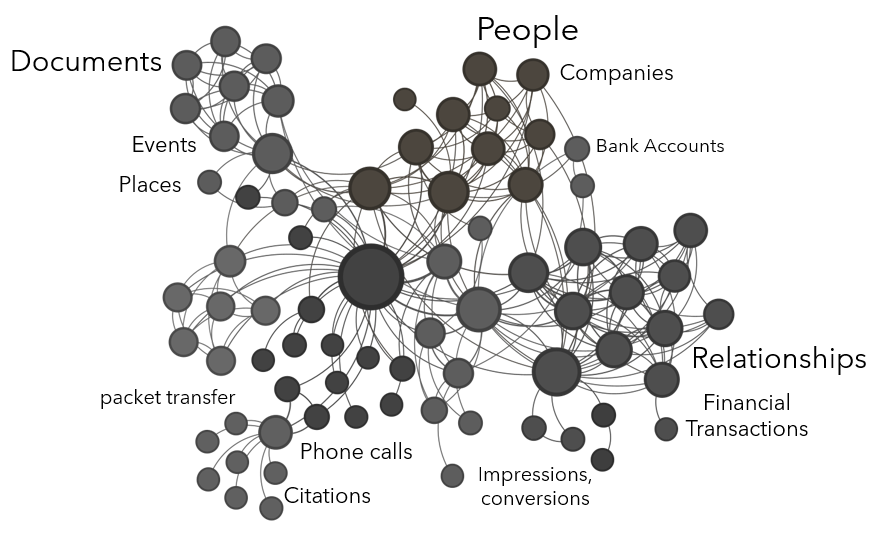
The domain of graph-based solutions includes an analytical environment (often powered by a graph database), graph analytic techniques, and graph visualization techniques. Graphs, like most analytic tools, require specific use cases. Graphs can be used to visualize connections within and across datasets, to discover latent connections, to simulate the dissemination of information or model contagion, to model network traffic or social behavior, to identify most influential actors in a social network, and many other use cases. Who is using the graph? What are these users trying to accomplish analytically and/or visually? Are they exploring an organization’s data? Are they answering specific questions? Are they analyzing, modeling, simulating, predicting? Understanding the use cases the graph-based solution needs to address is the first step to establishing the purpose of the graph and identifying the graph’s domain.
Probably the biggest mistake in implementing graph-based solutions is the attempt to create the master graph. One Graph to Rule Them All. In other words, all enterprise data in one graph. Graph is not a Master Data Management (MDM) solution nor is it a replacement for a data warehouse, even if the organization has a scalable graph database in place. The most successful graphs represent a given domain of analytic inquiry. For example, a financial intelligence graph may contain companies, beneficial ownership structures, financial transactions, financial institutions, and high net worth individuals. A pattern-of-life locational graph may contain high-volume signals data such as IP addresses and mobile phone data, alongside physical locations, technical assets, and individuals. Once a graph’s purpose and domain are clear, architects can move on to the data available and/or required to construct the graph.
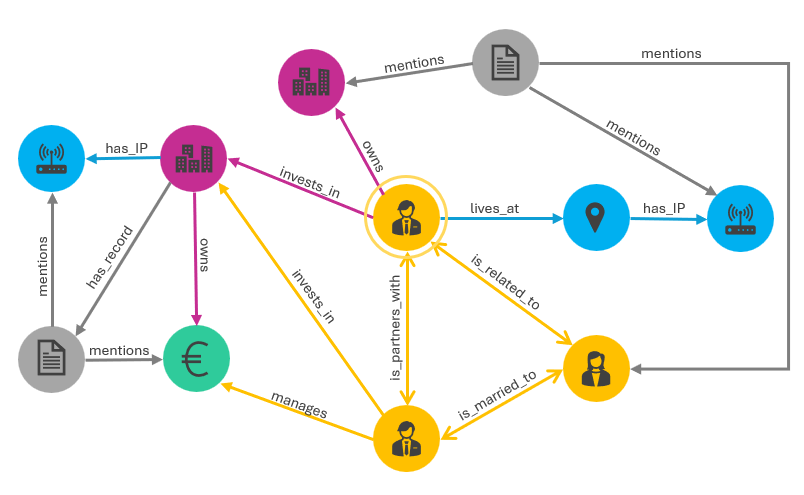
A graph that lives in a graph database will have a schema that dictates its structure. In other words, the schema will specify the types of entities that exist in the graph and the relationships that are permitted between them. One benefit of a graph database over other database types is that the schema is flexible and can be updated as new data, entities, and relationship types are added to the graph over time. Graph data engineers make many decisions when designing a graph database to represent the ontology — the conceptual structure of a dataset — in a schema that makes sense for the graph being created. If the data are well understood in the organization, frequently the graph architecting process can begin with schema creation, but if the nature of the graph and inclusive datasets is more exploratory, ontology design may be required first.
Consider the sample schema in the image below. There are five entity types: people (yellow), physical and virtual locations (blue), documents (gray), companies (pink), and financial accounts (green). Between entities, several relationship types are permitted, e.g., “is_related_to”, “mentions”, and “invests_in”. This is a directed graph meaning that the directionality of the relationship has meaning, i.e., two people are_married_to each other (bidirectional link) and a person lives_at a place (directed link).
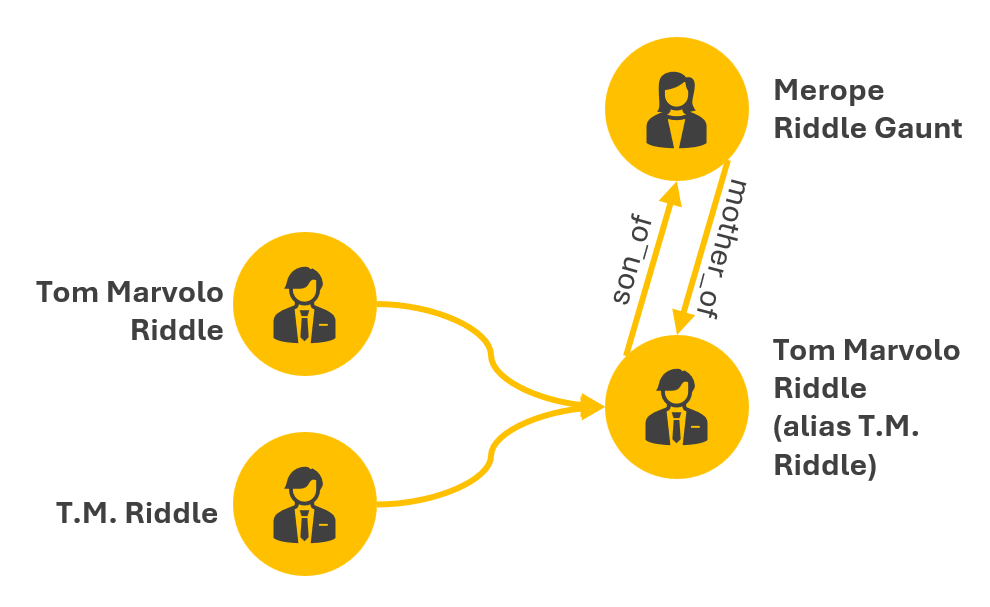
Connections between entities across datasets may not always be explicit in the data. Simply importing two datasets into a graph environment could result in many nodes with no connections between them.
Consider a medical dataset that has a Tom Marvolo Riddle entry and a voter registration dataset that has a T.M. Riddle entry and a Merope Riddle Gaunt entry. In the medical dataset, Merope Gaunt is listed as Tom Riddle’s mother. In the voter registration dataset, there are no family members described. How do the Tom Marvolo Riddle and T.M. Riddle entries get deduplicated when merging the datasets in the graph?, i.e., there should not be two separate nodes in the graph for Tom Riddle and T.M. Riddle as they are the same person. How do Tom Riddle and Merope Gaunt get connected, and how is their connection specified as in the image below?, e.g., connected, related, mother/son? Is the relationship weighted?
These questions require not only a data engineering team to specify the graph schema and implement the graph’s design, but also some sort of entity resolution process, which I have written about previously.
Graph data are pre-joined in graph data storage, meaning that one-hop queries run faster than in traditional databases, e.g., query Tom Riddle and see all of his immediate connections. Analytical operations on graphs, however, are quite slow, e.g., ‘show me the shortest path between Tom Riddle and Minerva McGonagall’, or ‘which character has the highest eigenvector centrality in Harry Potter and the Half Blood Prince’? As a general rule, latency in graph operations increases exponentially with graph density (a ratio of existing connections in the graph to all possible connections in the graph). Most graph visualization tools struggle to render several tens of thousands of nodes on screen.
If an organization is pursuing scalable graph solutions for multiple concurrent analyst users, a bespoke graph data architecture is required. This includes a scalable graph database, several graph data engineering processes, and a front-end visualization tool.
Once a graph solution is built, one of the biggest challenges is how to maintain it. Connecting five datasets in a graph database and rendering the resultant graph analysis environment produces a snapshot in time. What is the periodicity of those datasets and how frequently does the graph need to be updated, i.e., weekly, monthly, quarterly, real-time? Are data overwritten or appended? Are removed entities removed from the graph or persisted? How are the updated datasets provided, i.e., delta tables, the entire dataset provided again? If there are temporal elements to the data, how are they represented?
Graphs are beautiful. They are human-intuitive, compelling, and highly visual. Conceptually, they are deceptively simple. Gather some datasets, specify the relationships between the datasets, merge data together, a graph is born. Analyze the graph, render pretty pictures. But the data engineering challenges associated with architecting a scalable graph-based solution are not trivial.
Tool and technology selection, schema design, graph data engineering, approaches to entity resolution and data deduplication, and architecting well for intended use are just some of the challenges. The important thing is to have a true graph team at the helm of designing an enterprise graph-based solution. A graph visualization capability does not a graph solution make. And a simple point-and-click self-serve software might work for a single analyst user, but is a far cry from an organizationally-relevant graph analytics environment. Graph data engineers, methodologists, and solution architects with graph experience are required to build a high-fidelity graph-based solution in light of all the challenges mentioned above.
I’ve seen graphs change many real-world analytic organizations. Regardless of the analytic domain, so much of an analyst’s work is manual. Numerous technology products exist that attempt to automate analyst workflows or create point-and-click solutions. Despite these efforts, the fundamental problem remains — the data an analyst requires are rarely readily accessible through one interface, much less interconnected and ready for iterative exploration. Data are provisioned to analysts through a variety of platforms, Application Programming Interfaces (APIs), and query tools, all of which require varying levels of technical acumen to access. It is then up to the analyst to manually synthesize the data and draw meaningful analytic conclusions.
Graph-based solutions comingle all an analyst’s relevant data together in one place and represents it intuitively. This gives the analyst the ability to quickly click through the entities and connections as appropriate for analysis. I have personally helped teams build anti-money laundering solutions, target bad actors and illicit financial transactions, interdict migrants lost at sea, track the movement of illegal substance, address illegal wildlife trafficking, and predict migration routes all with graph-based solutions. Unlocking the power of graph solutions for analytic enterprises begins with building a great graph — a solid foundation on which to build stronger, more impactful analytic inquiry.
What It Takes To Build a Great Graph was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
What It Takes To Build a Great Graph
Go Here to Read this Fast! What It Takes To Build a Great Graph
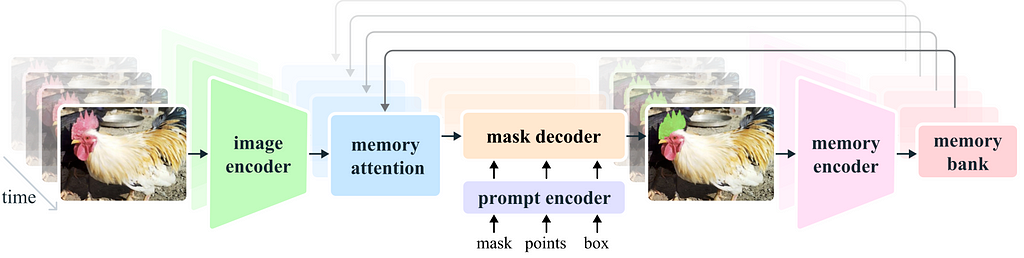

SAM2 (Segment Anything 2) is a new model by Meta aiming to segment anything in an image without being limited to specific classes or domains. What makes this model unique is the scale of data on which it was trained: 11 million images, and 11 billion masks. This extensive training makes SAM2 a powerful starting point for training on new image segmentation tasks.
The question you might ask is if SAM can segment anything why do we even need to retrain it? The answer is that SAM is very good at common objects but can perform rather poorly on rare or domain-specific tasks.
However, even in cases where SAM gives insufficient results, it is still possible to significantly improve the model’s ability by fine-tuning it on new data. In many cases, this will take less training data and give better results then training a model from scratch.
This tutorial demonstrates how to fine-tune SAM2 on new data in just 60 lines of code (excluding comments and imports).
The full training script of the can be found in:

The main way SAM works is by taking an image and a point in the image and predicting the mask of the segment that contains the point. This approach enables full image segmentation without human intervention and with no limits on the classes or types of segments (as discussed in a previous post).
The procedure for using SAM for full image segmentation:
While SAM can also utilize other inputs like masks or bounding boxes, these are mainly relevant for interactive segmentation involving human input. For this tutorial, we’ll focus on fully automatic segmentation and will only consider single points input.
More details on the model are available on the project website.
The SAM2 can be downloaded from:
If you don’t want to copy the training code, you can also download my forked version that already contains the TRAIN.py script.
Follow the installation instructions on the github repository.
In general, you need Python >=3.11 and PyTorch.
In addition, we will use OpenCV this can be installed using:
pip install opencv-python
You also need to download the pre-trained model from:
https://github.com/facebookresearch/segment-anything-2?tab=readme-ov-file#download-checkpoints
There are several models you can choose from all compatible with this tutorial. I recommend using the small model which is the fastest to train.
The next step is to download the dataset that will be used to fine-tune the model. For this tutorial, we will use the LabPics1 dataset for segmenting materials and liquids. You can download the dataset from this URL:
https://zenodo.org/records/3697452/files/LabPicsV1.zip?download=1
The first thing we need to write is the data reader. This will read and prepare the data for the net.
The data reader needs to produce:
Lets start by loading dependencies:
import numpy as np
import torch
import cv2
import os
from sam2.build_sam import build_sam2
from sam2.sam2_image_predictor import SAM2ImagePredictor
Next we list all the images in the dataset:
data_dir=r"LabPicsV1//" # Path to LabPics1 dataset folder
data=[] # list of files in dataset
for ff, name in enumerate(os.listdir(data_dir+"Simple/Train/Image/")): # go over all folder annotation
data.append({"image":data_dir+"Simple/Train/Image/"+name,"annotation":data_dir+"Simple/Train/Instance/"+name[:-4]+".png"})
Now for the main function that will load the training batch. The training batch includes: One random image, all the segmentation masks belong to this image, and a random point in each mask:
def read_batch(data): # read random image and its annotaion from the dataset (LabPics)
# select image
ent = data[np.random.randint(len(data))] # choose random entry
Img = cv2.imread(ent["image"])[...,::-1] # read image
ann_map = cv2.imread(ent["annotation"]) # read annotation
# resize image
r = np.min([1024 / Img.shape[1], 1024 / Img.shape[0]]) # scalling factor
Img = cv2.resize(Img, (int(Img.shape[1] * r), int(Img.shape[0] * r)))
ann_map = cv2.resize(ann_map, (int(ann_map.shape[1] * r), int(ann_map.shape[0] * r)),interpolation=cv2.INTER_NEAREST)
# merge vessels and materials annotations
mat_map = ann_map[:,:,0] # material annotation map
ves_map = ann_map[:,:,2] # vessel annotaion map
mat_map[mat_map==0] = ves_map[mat_map==0]*(mat_map.max()+1) # merged map
# Get binary masks and points
inds = np.unique(mat_map)[1:] # load all indices
points= []
masks = []
for ind in inds:
mask=(mat_map == ind).astype(np.uint8) # make binary mask
masks.append(mask)
coords = np.argwhere(mask > 0) # get all coordinates in mask
yx = np.array(coords[np.random.randint(len(coords))]) # choose random point/coordinate
points.append([[yx[1], yx[0]]])
return Img,np.array(masks),np.array(points), np.ones([len(masks),1])
The first part of this function is choosing a random image and loading it:
ent = data[np.random.randint(len(data))] # choose random entry
Img = cv2.imread(ent["image"])[...,::-1] # read image
ann_map = cv2.imread(ent["annotation"]) # read annotation
Note that OpenCV reads images as BGR while SAM expects images as RGB, using […,::-1] to change the image from BGR to RGB.
Note that OpenCV reads images as BGR while SAM expects RGB images. By using […,::-1] we change the image from BGR to RGB.
SAM expects the image size to not exceed 1024, so we are going to resize the image and the annotation map to this size.
r = np.min([1024 / Img.shape[1], 1024 / Img.shape[0]]) # scalling factor
Img = cv2.resize(Img, (int(Img.shape[1] * r), int(Img.shape[0] * r)))
ann_map = cv2.resize(ann_map, (int(ann_map.shape[1] * r), int(ann_map.shape[0] * r)),interpolation=cv2.INTER_NEAREST)
An important point here is that when resizing the annotation map (ann_map) we use INTER_NEAREST mode (nearest neighbors). In the annotation map, each pixel value is the index of the segment it belongs to. As a result, it’s important to use resizing methods that do not introduce new values to the map.
The next block is specific to the format of the LabPics1 dataset. The annotation map (ann_map) contains a segmentation map for the vessels in the image in one channel, and another map for the materials annotation in a different channel. We going to merge them into a single map.
mat_map = ann_map[:,:,0] # material annotation map
ves_map = ann_map[:,:,2] # vessel annotaion map
mat_map[mat_map==0] = ves_map[mat_map==0]*(mat_map.max()+1) # merged map
What this gives us is a a map (mat_map) in which the value of each pixel is the index of the segment to which it belongs (for example: all cells with value 3 belong to segment 3). We want to transform this into a set of binary masks (0/1) where each mask corresponds to a different segment. In addition, from each mask, we want to extract a single point.
inds = np.unique(mat_map)[1:] # list of all indices in map
points= [] # list of all points (one for each mask)
masks = [] # list of all masks
for ind in inds:
mask = (mat_map == ind).astype(np.uint8) # make binary mask for index ind
masks.append(mask)
coords = np.argwhere(mask > 0) # get all coordinates in mask
yx = np.array(coords[np.random.randint(len(coords))]) # choose random point/coordinate
points.append([[yx[1], yx[0]]])
return Img,np.array(masks),np.array(points), np.ones([len(masks),1])
This is it! We got the image (Img), a list of binary masks corresponding to segments in the image (masks), and for each mask the coordinate of a single point inside the mask (points).

Now lets load the net:
sam2_checkpoint = "sam2_hiera_small.pt" # path to model weight
model_cfg = "sam2_hiera_s.yaml" # model config
sam2_model = build_sam2(model_cfg, sam2_checkpoint, device="cuda") # load model
predictor = SAM2ImagePredictor(sam2_model) # load net
First, we set the path to the model weights in: sam2_checkpoint parameter. We downloaded the weights earlier from here. “sam2_hiera_small.pt” refer to the small model but the code will work for any model you choose. Whichever model you choose you need to set the corresponding config file in the model_cfg parameter. The config files are already located in the sub folder “sam2_configs/” of the main repository.
Before setting training parameters we need to understand the basic structure of the SAM model.
SAM is composed of three parts:
1) Image encoder, 2) Prompt encoder, 3) Mask decoder.
The image encoder is responsible for processing the image and creating the embedding that represents the image. This part consists of a VIT transformer and is the largest component of the net. We usually don’t want to train it, as it already gives good representation and training will demand lots of resources.
The prompt encoder processes the additional input to the net, in our case the input point.
The mask decoder takes the output of the image encoder and prompt encoder and produces the final segmentation masks. In general, we want to train only the mask decoder and maybe the prompt encoder. These parts are lightweight and can be fine-tuned fast with a modest GPU.
We can enable the training of the mask decoder and prompt encoder by setting:
predictor.model.sam_mask_decoder.train(True) # enable training of mask decoder
predictor.model.sam_prompt_encoder.train(True) # enable training of prompt encoder
Next, we define the standard adamW optimizer:
optimizer=torch.optim.AdamW(params=predictor.model.parameters(),lr=1e-5,weight_decay=4e-5)
We also going to use mixed precision training which is just a more memory-efficient training strategy:
scaler = torch.cuda.amp.GradScaler() # set mixed precision
Now lets build the main training loop. The first part is reading and preparing the data:
for itr in range(100000):
with torch.cuda.amp.autocast(): # cast to mix precision
image,mask,input_point, input_label = read_batch(data) # load data batch
if mask.shape[0]==0: continue # ignore empty batches
predictor.set_image(image) # apply SAM image encoder to the image
First we cast the data to mix precision for efficient training:
with torch.cuda.amp.autocast():
Next, we use the reader function we created earlier to read training data:
image,mask,input_point, input_label = read_batch(data)
We take the image we loaded and pass it through the image encoder (the first part of the net):
predictor.set_image(image)
Next, we process the input points using the net prompt encoder:
mask_input, unnorm_coords, labels, unnorm_box = predictor._prep_prompts(input_point, input_label, box=None, mask_logits=None, normalize_coords=True)
sparse_embeddings, dense_embeddings = predictor.model.sam_prompt_encoder(points=(unnorm_coords, labels),boxes=None,masks=None,)
Note that in this part we can also input boxes or masks but we are not going to use these options.
Now that we encoded both the prompt (points) and the image we can finally predict the segmentation masks:
batched_mode = unnorm_coords.shape[0] > 1 # multi mask prediction
high_res_features = [feat_level[-1].unsqueeze(0) for feat_level in predictor._features["high_res_feats"]]
low_res_masks, prd_scores, _, _ = predictor.model.sam_mask_decoder(image_embeddings=predictor._features["image_embed"][-1].unsqueeze(0),image_pe=predictor.model.sam_prompt_encoder.get_dense_pe(),sparse_prompt_embeddings=sparse_embeddings,dense_prompt_embeddings=dense_embeddings,multimask_output=True,repeat_image=batched_mode,high_res_features=high_res_features,)
prd_masks = predictor._transforms.postprocess_masks(low_res_masks, predictor._orig_hw[-1])# Upscale the masks to the original image resolution
The main part in this code is the model.sam_mask_decoder which runs the mask_decoder part of the net and generates the segmentation masks (low_res_masks) and their scores (prd_scores).
These masks are in lower resolution than the original input image and are resized to the original input size in the postprocess_masks function.
This gives us the final prediction of the net: 3 segmentation masks (prd_masks) for each input point we used and the masks scores (prd_scores). prd_masks contains 3 predicted masks for each input point but we only going to use the first mask for each point. prd_scores contains a score of how good the net thinks each mask is (or how sure it is in the prediction).
Now we have the net predictions we can calculate the loss. First, we calculate the segmentation loss, which means how good the predicted mask is compared to the ground true mask. For this, we use the standard cross entropy loss.
First we need to convert prediction masks (prd_mask) from logits into probabilities using the sigmoid function:
prd_mask = torch.sigmoid(prd_masks[:, 0])# Turn logit map to probability map
Next we convert the ground truth mask into a torch tensor:
prd_mask = torch.sigmoid(prd_masks[:, 0])# Turn logit map to probability map
Finally, we calculate the cross entropy loss (seg_loss) manually using the ground truth (gt_mask) and predicted probability maps (prd_mask):
seg_loss = (-gt_mask * torch.log(prd_mask + 0.00001) - (1 - gt_mask) * torch.log((1 - prd_mask) + 0.00001)).mean() # cross entropy loss
(we add 0.0001 to prevent the log function from exploding for zero values).
In addition to the masks, the net also predicts the score for how good each predicted mask is. Training this part is less important but can be useful . To train this part we need to first know what is the true score of each predicted mask. Meaning, how good the predicted mask actually is. We are going to do it by comparing the GT mask and the corresponding predicted mask using intersection over union (IOU) metrics. IOU is simply the overlap between the two masks, divided by the combined area of the two masks. First, we calculate the intersection between the predicted and GT mask (the area in which they overlap):
inter = (gt_mask * (prd_mask > 0.5)).sum(1).sum(1)
We use threshold (prd_mask > 0.5) to turn the prediction mask from probability to binary mask.
Next, we get the IOU by dividing the intersection by the combined area (union) of the predicted and gt masks:
iou = inter / (gt_mask.sum(1).sum(1) + (prd_mask > 0.5).sum(1).sum(1) - inter)
We going to use the IOU as the true score for each mask, and get the score loss as the absolute difference between the predicted scores and the IOU we just calculated.
score_loss = torch.abs(prd_scores[:, 0] - iou).mean()
Finally, we merge the segmentation loss and score loss (giving much higher weight to the first):
loss = seg_loss+score_loss*0.05 # mix losses
Once we get the loss everything is completely standard. We calculate backpropogation and update weights using the optimizer we made earlier:
predictor.model.zero_grad() # empty gradient
scaler.scale(loss).backward() # Backpropogate
scaler.step(optimizer)
scaler.update() # Mix precision
We also want to save the trained model once every 1000 steps:
if itr%1000==0: torch.save(predictor.model.state_dict(), "model.torch") # save model
Since we already calculated the IOU we can display it as a moving average to see how well the model prediction are improving over time:
if itr==0: mean_iou=0
mean_iou = mean_iou * 0.99 + 0.01 * np.mean(iou.cpu().detach().numpy())
print("step)",itr, "Accuracy(IOU)=",mean_iou)
And that it, we have trained/ fine-tuned the Segment-Anything 2 in less than 60 lines of code (not including comments and imports). After about 25,000 steps you should see major improvement .
The model will be saved to “model.torch”.
You can find the full training code at:
To see how to load and use the model we just trained check the next section.
Now that the model as been fine-tuned, let’s use it to segment an image.
We going to do this using the following steps:
The full code for doing that is available at:
First, we load the dependencies and cast the weights to float16 this makes the model much faster to run (only possible for inference).
import numpy as np
import torch
import cv2
from sam2.build_sam import build_sam2
from sam2.sam2_image_predictor import SAM2ImagePredictor
# use bfloat16 for the entire script (memory efficient)
torch.autocast(device_type="cuda", dtype=torch.bfloat16).__enter__()
Next, we load a sample image and a mask of the image region we want to segment (download image/mask):
image_path = r"sample_image.jpg" # path to image
mask_path = r"sample_mask.png" # path to mask, the mask will define the image region to segment
def read_image(image_path, mask_path): # read and resize image and mask
img = cv2.imread(image_path)[...,::-1] # read image as rgb
mask = cv2.imread(mask_path,0) # mask of the region we want to segment
# Resize image to maximum size of 1024
r = np.min([1024 / img.shape[1], 1024 / img.shape[0]])
img = cv2.resize(img, (int(img.shape[1] * r), int(img.shape[0] * r)))
mask = cv2.resize(mask, (int(mask.shape[1] * r), int(mask.shape[0] * r)),interpolation=cv2.INTER_NEAREST)
return img, mask
image,mask = read_image(image_path, mask_path)
Sample 30 random points inside the region we want to segment:
num_samples = 30 # number of points/segment to sample
def get_points(mask,num_points): # Sample points inside the input mask
points=[]
for i in range(num_points):
coords = np.argwhere(mask > 0)
yx = np.array(coords[np.random.randint(len(coords))])
points.append([[yx[1], yx[0]]])
return np.array(points)
input_points = get_points(mask,num_samples)
Load the standard SAM model (same as in training)
# Load model you need to have pretrained model already made
sam2_checkpoint = "sam2_hiera_small.pt"
model_cfg = "sam2_hiera_s.yaml"
sam2_model = build_sam2(model_cfg, sam2_checkpoint, device="cuda")
predictor = SAM2ImagePredictor(sam2_model)
Next, Load the weights of the model we just trained (model.torch):
predictor.model.load_state_dict(torch.load("model.torch"))
Run the fine-tuned model to predict a segmentation mask for every point we selected earlier:
with torch.no_grad(): # prevent the net from caclulate gradient (more efficient inference)
predictor.set_image(image) # image encoder
masks, scores, logits = predictor.predict( # prompt encoder + mask decoder
point_coords=input_points,
point_labels=np.ones([input_points.shape[0],1])
)
Now we have a list of predicted masks and their scores. We want to somehow stitch them into a single consistent segmentation map. However, many of the masks overlap and might be inconsistent with each other.
The approach to stitching is simple:
First we will sort the predicted masks according to their predicted scores:
masks=masks[:,0].astype(bool)
shorted_masks = masks[np.argsort(scores[:,0])][::-1].astype(bool)
Now lets create an empty segmentation map and occupancy map:
seg_map = np.zeros_like(shorted_masks[0],dtype=np.uint8)
occupancy_mask = np.zeros_like(shorted_masks[0],dtype=bool)
Next, we add the masks one by one (from high to low score) to the segmentation map. We only add a mask if it’s consistent with the masks that were previously added, which means only if the mask we want to add has less than 15% overlap with already occupied areas.
for i in range(shorted_masks.shape[0]):
mask = shorted_masks[i]
if (mask*occupancy_mask).sum()/mask.sum()>0.15: continue
mask[occupancy_mask]=0
seg_map[mask]=i+1
occupancy_mask[mask]=1
And this is it.
seg_mask now contains the predicted segmentation map with different values for each segment and 0 for the background.
We can turn this into a color map using:
rgb_image = np.zeros((seg_map.shape[0], seg_map.shape[1], 3), dtype=np.uint8)
for id_class in range(1,seg_map.max()+1):
rgb_image[seg_map == id_class] = [np.random.randint(255), np.random.randint(255), np.random.randint(255)]
And display:
cv2.imshow("annotation",rgb_image)
cv2.imshow("mix",(rgb_image/2+image/2).astype(np.uint8))
cv2.imshow("image",image)
cv2.waitKey()

The full inference code is available at:
That’s it, we have trained and tested SAM2 on a custom dataset. Other than changing the data-reader, this should work for any dataset. In many cases, this should be enough to give a significant improvement in performance.
If this is not the case, there is more we can do: Since we only fine-tuned the final part of the net (mask-decoder) we gave it a limited capacity to learn. The main part of SAM2 is the image encoder. This is the bulk part of the net and fine-tuning it will take more data and a stronger GPU, but will give the net more room for improvement.
You can train this part by adding the command:
predictor.model.image_encoder.train(True)
Note that in this case, you will also need to scan the SAM2 code for “no_grad” commands and remove them (“ no_grad” blocks the gradient collection, which saves memory but prevents training).
Finally, SAM2 can also segment and track objects in videos, but fine-tuning this part is for another time.
Copyright: All images for the post are taken from the SAM2 GIT repository (under Apache license), and LabPics dataset (under MIT license). This tutorial code and nets are available under the Apache license.
Train/Fine-Tune Segment Anything 2 (SAM 2) in 60 Lines of Code was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Train/Fine-Tune Segment Anything 2 (SAM 2) in 60 Lines of Code
Go Here to Read this Fast! Train/Fine-Tune Segment Anything 2 (SAM 2) in 60 Lines of Code

Originally appeared here:
Snowflake Arctic models are now available in Amazon SageMaker JumpStart
Go Here to Read this Fast! Snowflake Arctic models are now available in Amazon SageMaker JumpStart