
Originally appeared here:
Improve RAG performance using Cohere Rerank
Go Here to Read this Fast! Improve RAG performance using Cohere Rerank
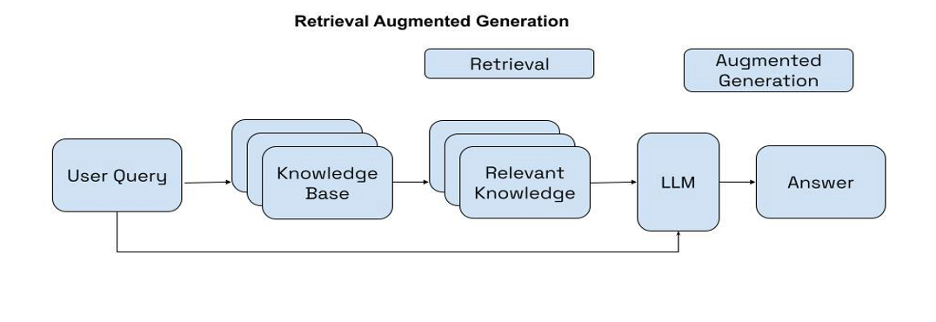

Originally appeared here:
Improve RAG performance using Cohere Rerank
Go Here to Read this Fast! Improve RAG performance using Cohere Rerank

I recently read a September 4th thread on Bluesky by Dr. Johnathan Flowers of American University about the dustup that occurred when organizers of NaNoWriMo put out a statement saying that they approved of people using generative AI such as LLM chatbots as part of this year’s event.
“Like, art is often the ONE PLACE where misfitting between the disabled bodymind and the world can be overcome without relying on ablebodied generosity or engaging in forced intimacy. To say that we need AI help is to ignore all of that.” –Dr. Johnathan Flowers, Sept 4 2024
Dr. Flowers argued that by specifically calling out this decision as an attempt to provide access to people with disabilities and marginalized groups, the organizers were downplaying the capability of these groups to be creative and participate in art. As a person with a disability himself, he notes that art is one of a relatively few places in society where disability may not be a barrier to participation in the same way it is in less accessible spaces.
Since the original announcement and this and much other criticism, the NaNoWriMo organizers have softened or walked back some of their statement, with the most recent post seeming to have been augmented earlier this week. Unfortunately, as so often happens, much of this conversation on social media devolved into an unproductive discussion.
I’ve talked in this space before about the difficulty in assessing what it really means when generative AI is involved in art, and I still stand by my point that as a consumer of art, I am seeking a connection to another person’s perspective and view of the world, so AI-generated material doesn’t interest me in that way. However, I have not spent as much time thinking about the role of AI as accessibility tooling, and that’s what I’d like to discuss today.
I am not a person with physical disability, so I can only approach this topic as a social scientist and a viewer of that community from the outside. My views are my own, not those of any community or organization.
In a recent presentation, I was asked to begin with a definition of “AI”, which I always kind of dread because it’s so nebulous and difficult, but this time I took a fresh stab at it, and read some of the more recent regulatory and policy discussions, and came up with this:
AI: use of certain forms of machine learning to perform labor that otherwise must be done by people.
I’m still workshopping, and probably will be forever as the world changes, but I think this is useful for today’s discussion. Notice that this is NOT limiting our conversation to generative AI, and that’s important. This conversation about AI specifically relates to applying machine learning, whether it involves deep learning or not, to completing tasks that would not be automatable in any other way currently available to us.
Social theory around disability is its own discipline, with tremendous depth and complexity. As with discussions and scholarship examining other groups of people, it’s incredibly important for actual members of this community to have their voices not only heard, but to lead discussions about how they are treated and their opportunities in the broader society. Based on what I understand of the field, I want to prioritize concerns about people with disability having the amount of autonomy and independence they desire, with the amount of support necessary to have opportunities and outcomes comparable to people without disabilities. It’s also worth mentioning that much of the technology that was originally developed to aid people with disabilities is assistive to all people, such as automatic doors.
So, what role can AI really play in this objective? Is AI a net good for people with disabilities? Technology in general, not just AI related development, has been applied in a number of ways to provide autonomy and independence to people with disabilities that would not otherwise be possible. Anyone who has, like me, been watching the Paris Paralympics this past few weeks will be able to think of examples of technology in this way.
But I’m curious what AI provides to the table that isn’t otherwise there, and what the downsides or risks may be. Turns out, quite a bit of really interesting scholarly research has already been done on the question and continues to be released. I’m going to give a brief overview of a few key areas and provide more sources if you happen to be interested in a deeper dive in any of them.
This seems like it ought to be a good wheelhouse for AI tools. LLMs have great usefulness for restating, rephrasing, or summarizing texts. When individuals struggle with reading long texts/concentration, having the ability to generate accurate summaries can make the difference between a text’s themes being accessible to those people or not. This isn’t necessarily a substitution for the whole text, but just might be a tool augmenting the reader’s understanding. (Like Cliff Notes, but for the way they’re supposed to be used.) I wouldn’t recommend things like asking LLMs direct questions about the meaning of a passage, because that is more likely to produce error or inaccuracies, but summarizing a text that already exists is a good use case.
Secondarily, people with difficulty in either producing or consuming spoken communication can get support from AI tools. The technologies can either take spoken text and generate highly accurate automatic transcriptions, which may be easier for people with forms of aphasia to comprehend, or it can allow a person who struggles with speaking to write a text and convert this to a highly realistic sounding human spoken voice. (Really, AI synthetic voices are becoming so amazing recently!)
This is not even getting into the ways that AI can help people with hearing impairment, either! Hearing aids can use models to identify and isolate the sounds the user wants to focus on, and diminish distractions or background noise. Anyone who’s used active noise canceling is benefiting from this kind of technology, and it’s a great example of things that are helpful for people with and without disabilities both.
For people with visual impairments, there may be barriers to digital participation, including things like poorly designed websites for screen readers, as well as the lack of alt text describing the contents of images. Models are increasingly skilled at identifying objects or features within images, and this may be a highly valuable form of AI if made widely accessible so that screen reading software could generate its own alt text or descriptions of images.
There are also forms of AI that help prosthetics and physical accessibility tools work better. I don’t mean necessarily technologies using neural implants, although that kind of thing is being studied, but there are many models that learn the physics of human movement to help computerized powered prosthetics work better for people. These can integrate with muscles and nerve endings, or they can subtly automate certain movements that help with things like fine motor skills with upper limb prosthetics. Lower body limb prosthetics can use AI to better understand and produce stride lengths and fluidity, among other things.
Ok, so that is just a handful of the great things that AI can do for disability needs. However, we should also spend some time discussing the areas where AI can be detrimental for people with disabilities and our society at large. Most of these areas are about the cultural production using AI, and I think they are predominantly caused by the fact that these models replicate and reinforce social biases and discrimination.
For example:
This area has two major themes that have negative potential for people with disabilities.
When the medical community starts using AI in their work, we should take a close look at the side effects for marginalized communities including people with disabilities. Similarly to how LLM use can mean the actual voices of people with disabilities are overlooked in important decision making, if medical professionals are using LLMs to advise on the diagnosis or therapies for disabilities, this advice will be affected by the social and cultural negative biases that these models carry.
This might mean that non-stereotypical or uncommon presentations of disability may be overlooked or ignored, because models necessarily struggle to understand outliers and exceptional cases. It may also mean that patients have difficulty convincing providers of their lived experience when it runs counter to what a model expects or predicts. As I’ve discussed in other work, people can become too confident in the accuracy of machine learning models, and human perspectives can be seen as less trustworthy in comparison, even when this is not a justifiable assertion.
There are quite a few other technologies I haven’t had time to cover here, but I do want to make note that the mere existence of a technology is not the same thing as people with disabilities having easy, affordable access to these things to actually use. People with disabilities are often disadvantaged economically, in large part because of unnecessary barriers to economic participation, so many of the exceptional advances are not actually accessible to lots of the people who might need them. This is important to recognize as a problem our society needs to take responsibility for — as with other areas of healthcare in the United States in particular, we do a truly terrible job meeting people’s needs for the care and tools that would allow them to live their best lives and participate in the economy in the way they otherwise could.
This is only a cursory review of some of the key issues in this space, and I think it’s an important topic for those of us working in machine learning to be aware of. The technologies we build have benefits and risks both for marginalized populations, including people with disabilities, and our responsibility is to take this into account as we work and do our best to mitigate those risks.
https://slate.com/technology/2024/09/national-novel-writing-month-ai-bots-controversy.html
https://www.american.edu/cas/faculty/jflowers.cfm
Disability, Accessibility, and AI was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Disability, Accessibility, and AI
Go Here to Read this Fast! Disability, Accessibility, and AI
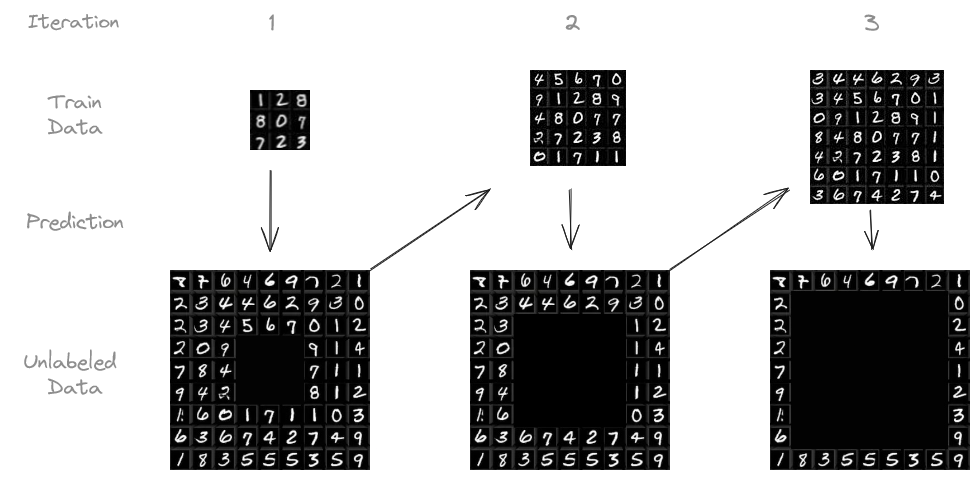

In machine learning, more data leads to better results. But labeling data can be expensive and time-consuming. What if we could use the huge amounts of unlabeled data that’s usually easy to get? This is where pseudo-labeling comes in handy.
TL;DR: I conducted a case study on the MNIST dataset and boosted my model’s accuracy from 90 % to 95 % by applying iterative, confidence-based pseudo-labeling. This article covers the details of what pseudo-labeling is, along with practical tips and insights from my experiments.
Pseudo-labeling is a type of semi-supervised learning. It bridges the gap between supervised learning (where all data is labeled) and unsupervised learning (where no data is labeled).

The exact procedure I followed goes as follows:
While this approach may introduce some incorrect labels, the benefit comes from the significantly increased amount of training data.
The idea of a model learning from its own predictions might raise some eyebrows. After all, aren’t we trying to create something from nothing, relying on an “echo chamber” where the model simply reinforces its own initial biases and errors?
This concern is valid. It may remind you of the legendary Baron Münchhausen, who famously claimed to have pulled himself and his horse out of a swamp by his own hair — a physical impossibility. Similarly, if a model solely relies on its own potentially flawed predictions, it risks getting stuck in a loop of self-reinforcement, much like people trapped in echo chambers who only hear their own beliefs reflected back at them.
So, can pseudo-labeling truly be effective without falling into this trap?
The answer is yes. While this story of Baron Münchhausen is obviously a fairytale, you may imagine a blacksmith progressing through the ages. He starts with basic stone tools (the initial labeled data). Using these, he forges crude copper tools (pseudo-labels) from raw ore (unlabeled data). These copper tools, while still rudimentary, allow him to work on previously unfeasible tasks, eventually leading to the creation of tools that are made of bronze, iron, and so on. This iterative process is crucial: You cannot forge steel swords using a stone hammer.
Just like the blacksmith, in machine learning, we can achieve a similar progression by:
Pseudo-labeling, when done right, can be a powerful tool to make the most of small labeled datasets, as we will see in the following case study.
I conducted my experiments on the MNIST dataset, a classic collection of 28 by 28 pixel images of handwritten digits, widely used for benchmarking machine learning models. It consists of 60,000 training images and 10,000 test images. The goal is to, based on the 28 by 28 pixels, predict what digit is written.
I trained a simple CNN on an initial set of 1,000 labeled images, leaving 59,000 unlabeled. I then used the trained model to predict the labels for the unlabeled images. Predictions with confidence above a certain threshold (e.g., 95 %) were added to the training set, along with their predicted labels. The model was then retrained on this expanded dataset. This process was repeated iteratively, up to ten times or until there was no more unlabeled data.
This experiment was repeated with different numbers of initially labeled images and confidence thresholds.
The following table summarizes the results of my experiments, comparing the performance of pseudo-labeling to training on the full labeled dataset.
Even with a small initial labeled dataset, pseudo-labeling may produce remarkable results, increasing the accuracy by 4.87 %pt. for 1,000 initial labeled samples. When using only 100 initial samples, this effect is even stronger. However, it would’ve been wise to manually label more than 100 samples.
Interestingly, the final test accuracy of the experiment with 100 initial training samples exceeded the share of correct training labels.




Looking at the above graphs, it becomes apparent that, in general, higher thresholds lead to better results — as long as at least some predictions exceed the threshold. In future experiments, one might try to vary the threshold with each iteration.
Furthermore, the accuracy improves even in the later iterations, indicating that the iterative nature provides a true benefit.
The repository containing the experiment’s code can be found here.
Related paper: Iterative Pseudo-Labeling with Deep Feature Annotation and Confidence-Based Sampling
Teaching Your Model to Learn from Itself was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Teaching Your Model to Learn from Itself
Go Here to Read this Fast! Teaching Your Model to Learn from Itself


Part 4 — Towards Mamba State Space Models for Images, Videos and Time Series
Originally appeared here:
Vision Mamba: Like a Vision Transformer but Better
Go Here to Read this Fast! Vision Mamba: Like a Vision Transformer but Better

In my previous article on Unit Disk and 2D Bounded KDE, I discussed the importance of being able to sample arbitrary distributions. This is especially relevant for applications like Monte Carlo integration, which is used to solve complex integrals, such as light scattering in Physically Based Rendering (PBRT).
Sampling in 2D introduces new challenges compared to 1D. This article focuses on uniformly sampling the 2D unit disk and visualizing how transformations applied to a standard [0,1] uniform random generator create different distributions.
We’ll also explore how these transformations, though yielding the same distribution, affect Monte Carlo integration by introducing distortion, leading to increased variance.
Random number generators often offer many predefined sampling distributions. However, for highly specific distributions, you’ll likely need to create your own. This involves combining and transforming basic distributions to achieve the desired outcome.
For instance, to uniformly sample the interval between a and b, you can apply an affine transform on the standard uniform sampling from [0,1].
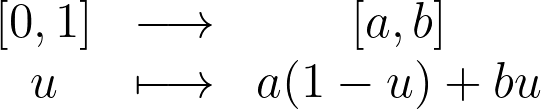
In this article, we’ll explore how to uniformly sample points within the 2D unit disk by building on the basic [0,1] uniform sampling.
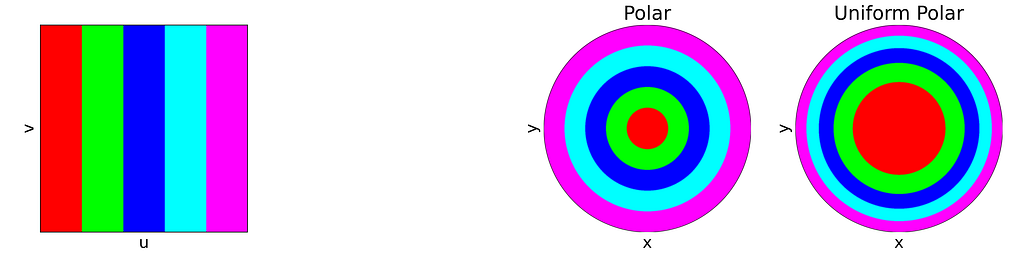
For readability, I’ve intentionally used the adjective “unit” in two different contexts in this article. The “unit square” refers to the [0,1]² domain, reflecting the range of the basic random generator. Conversely, the “unit disk” is described within [-1,1]² for convenience in polar coordinates. In practice, we can easily map between these using an affine transformation. We’ll denote u and v as samples drawn from the standard [0,1] or [-1,1] uniform distribution.
Using the [0,1] uniform sampling twice allows us to uniformly sample the unit square [0,1]².
A very simple approach known as “Rejection Sampling” consists in sampling the unit square and rejecting any sample falling outside the disk.
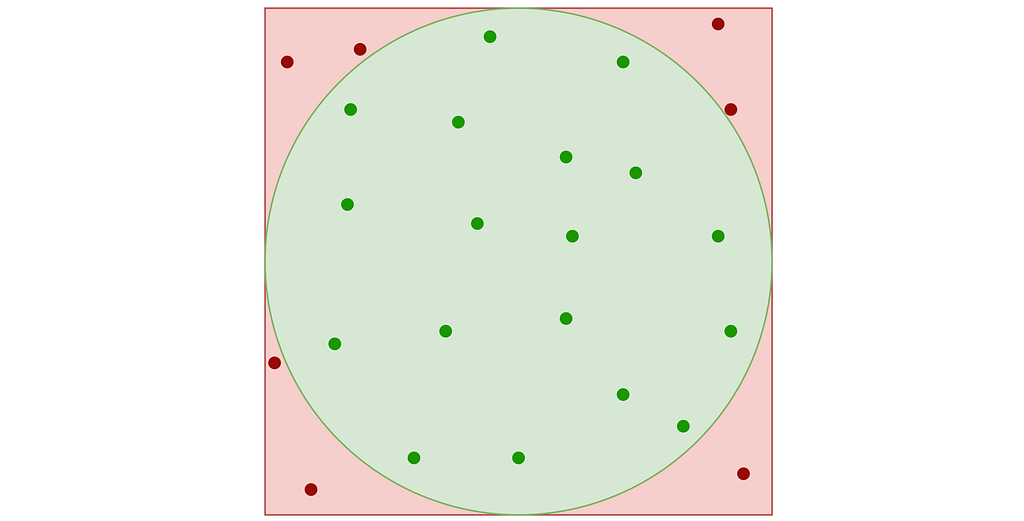
This results in points that follow a uniform 2D distribution within the disk contained in the unit square, as illustrated in the figure below.
The density maps in this article are generated by sampling many points from the specified distribution and then applying a Kernel Density Estimator. Methods for addressing boundary bias in the density are detailed in the previous article “Unit Disk and 2D Bounded KDE”.
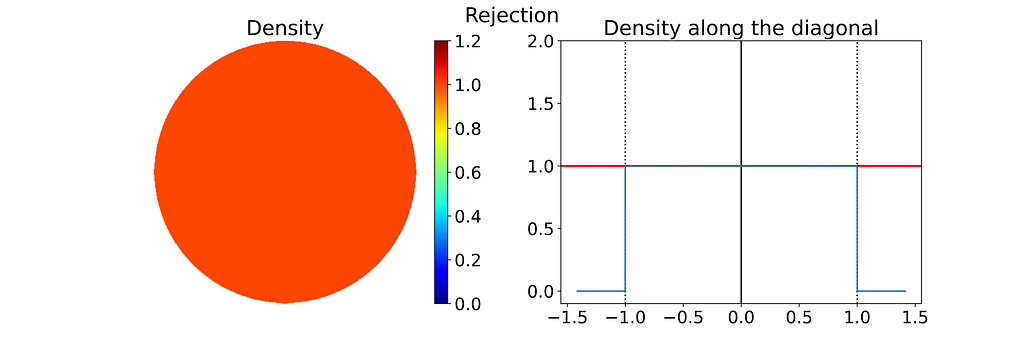
A major drawback is that rejection sampling can require many points to get the desired number of valid samples, with no upper limit on the total number, leading to inefficiencies and higher computational costs.
An intuitive approach is to use polar coordinates for uniform sampling: draw a radius within [0,1] and an angle within [0, 2π].
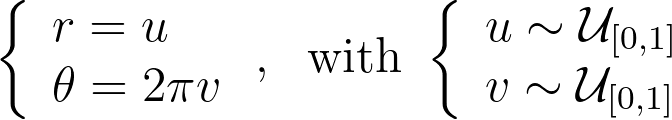
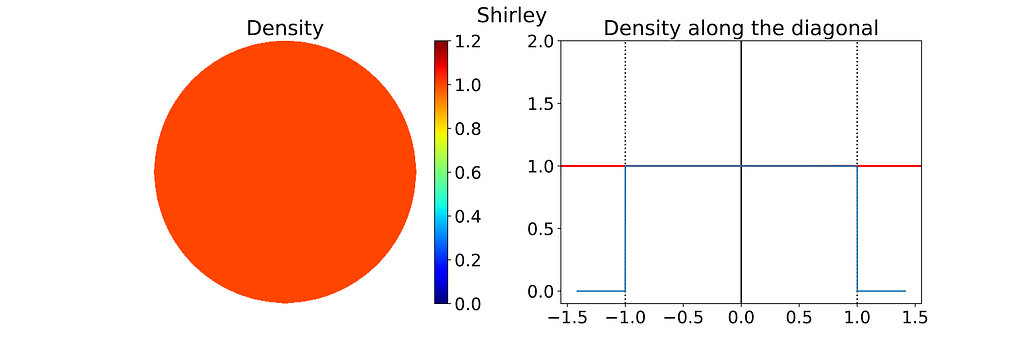
Both the radius and angle are uniform, what could possibly go wrong?However, this method leads to an infinite density singularity at the origin, as illustrated by the empirical density map below.
To ensure the linear colormap remains readable, the density map has been capped at an arbitrary maximum value of 10. Without this cap, the map would display a single red dot at the center of a blue disk.

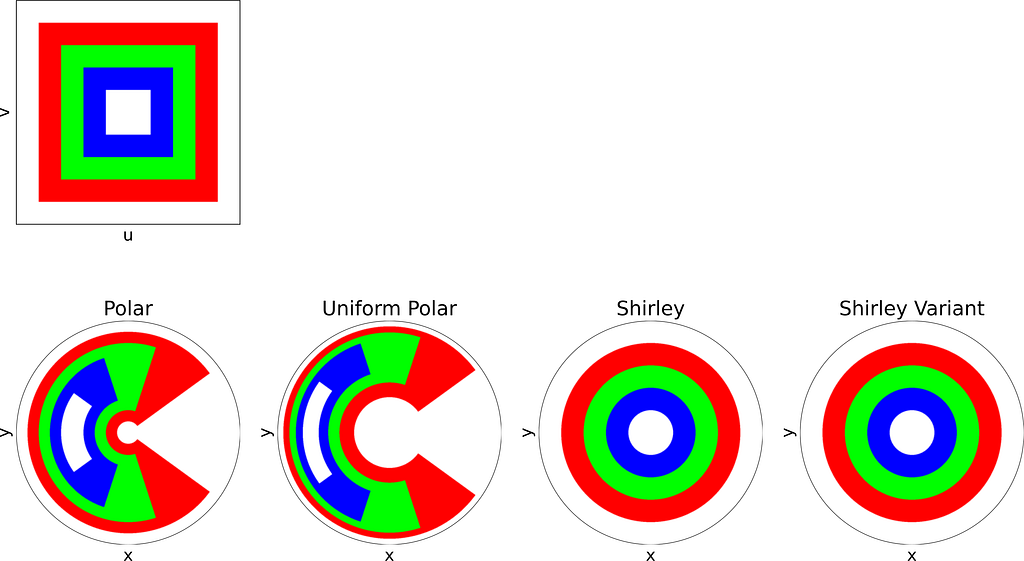
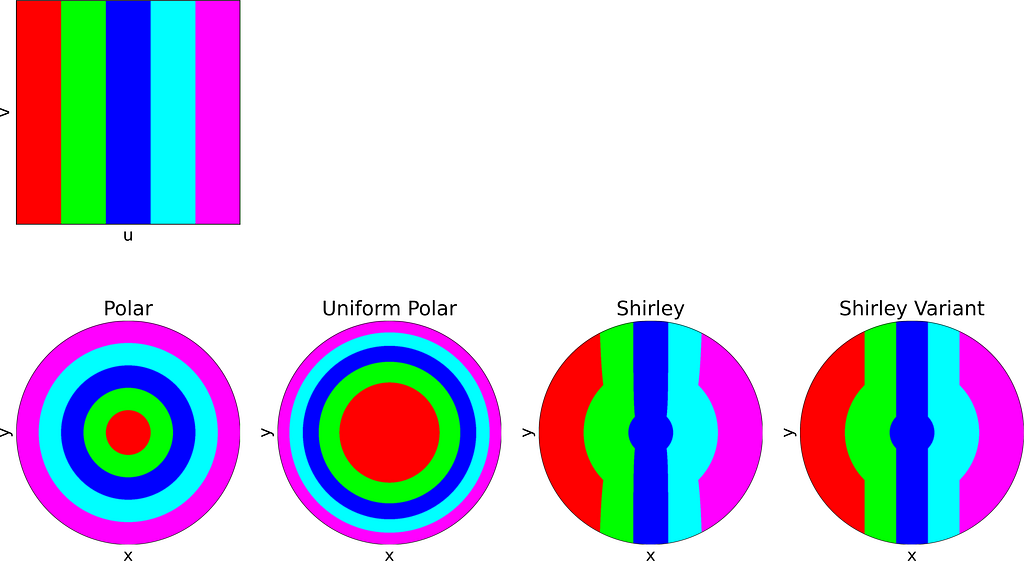
The figure below uses color to show how the unit square, sampled with (u,v), maps to the unit disk with (x,y) using the polar transform defined above. The colored areas in the square are equal, but this equality does not hold once mapped to the disk. This visually illustrates the density map: large radii exhibit much lower density, as they are distributed across a wider ring farther from the origin.

Let’s explore the mathematical details. When applying a transform T to a multi-dimensional random variable A, the resulting density is found by dividing by the absolute value of the determinant of the Jacobian of T.
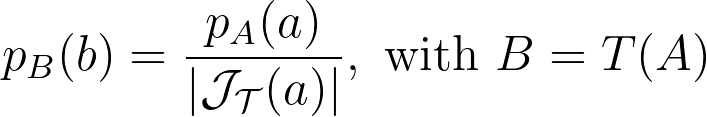
The polar transform is given by the equation below.

We can compute the determinant of its jacobian.
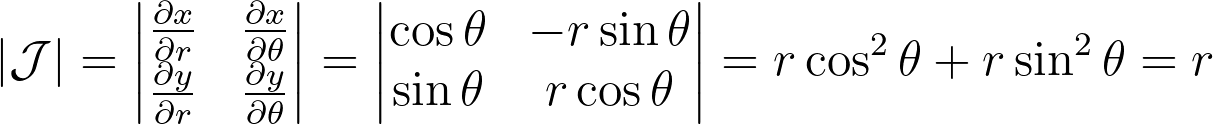
Thus, the polar transformation results in a density that is inversely proportional to the radius, explaining the observed singularity.

The 1D density profile along the diagonal shown above corresponds to the absolute value of the inverse function, which is then set to zero outside [-1, 1]. At first glance, this might seem counterintuitive, given that the 1D inverse function isn’t integrable over [-1, 1]! However, it’s essential to remember that the integration is performed in 2D using polar coordinates, not in 1D.
There are two ways to find the correct polar transform that results in an uniform distribution. Either by solving a differential equation or by using the inversion method. Let’s explore both approaches.
To address the heterogeneity in the radius, we introduce a function f to adjust it: r=f(u). The angle, however, is kept uniform due to the symmetry of the disk. We can then solve the differential equation that ensures the determinant of the corresponding Jacobian remains constant, to keep the same density.
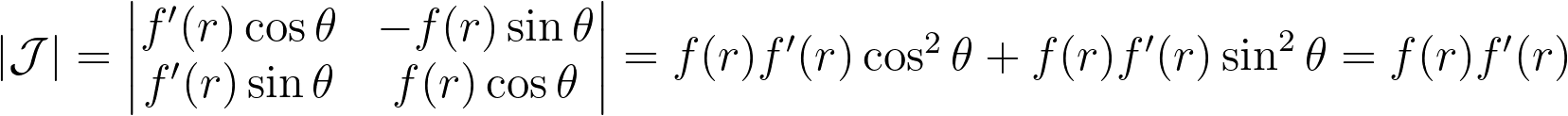
We get ff’=c, which has a unique solution given the boundary conditions f(0)=0 and f(1)=1. We end up with the following transform.
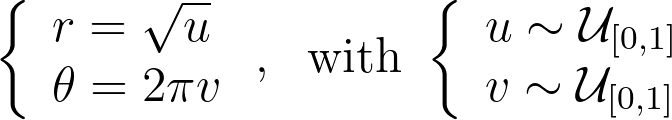
The inversion method is easier to grasp in the discrete case. Consider three possible values A, B and C with probabilities of 60%, 10%, and 30%, respectively. As shown in the figure below, we can stack these probabilities to reach a total height of 100%. By uniformly drawing a percentage U between 0% and 100% and mapping it to the corresponding value A, B or C on the stack, we can transform a uniform sampling into our discrete non‑uniform distribution.
This is very similar in the continuous case. The inversion method begins by integrating the probability distribution function (PDF) p of a 1D variable X to obtain the cumulative distribution function (CDF) P(X<x), which increases from 0 to 1. Then, by sampling a uniform variable U from [0,1] and applying the inverse CDF to U, we can obtain a sample x that follows the desired distribution p.
Assuming a uniform disk distribution p(x,y), we can deduce the corresponding polar distribution p(r,θ) to enforce.
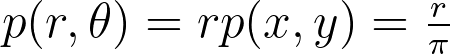
It turns out that this density p(r,θ) is separable, and we can independently sample r and θ from their respective expected 1D marginal densities using the inversion method.
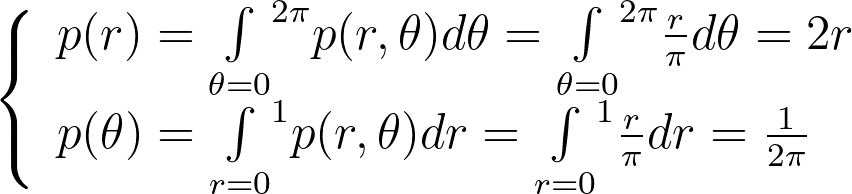
When the joint density isn’t separable, we first sample a variable from its marginal density and then draw the second variable from its conditional density given the first variable.
We integrate these marginal densities into CDFs.
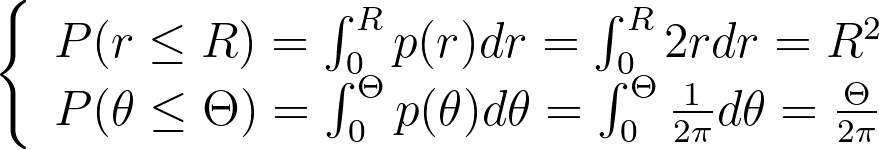
Sampling uniform (u,v) within [0,1] and applying the inverse CDFs gives us the following transform, which is the same as the one obtained above using the differential equation.
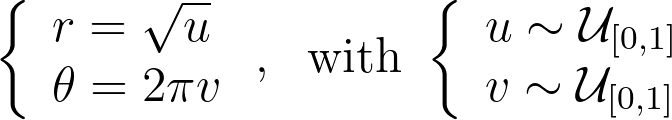
The resulting distribution is effectively uniform, as confirmed by the empirical density map shown below.
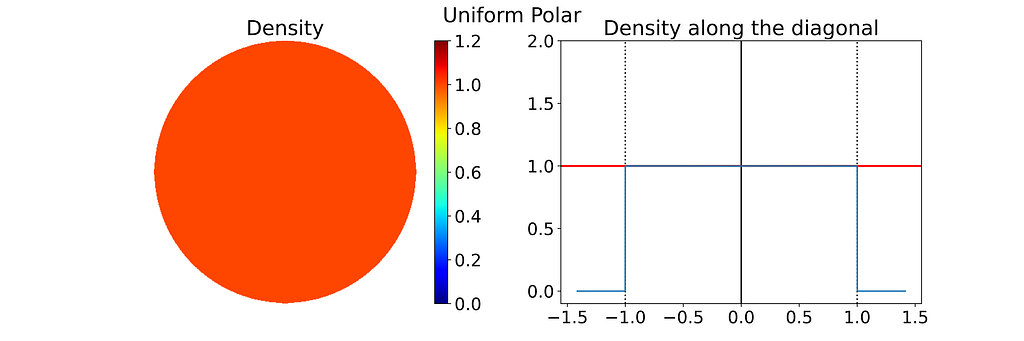
The square root function effectively adjusts the colored columns to preserve their relative areas when mapped to the disk.

In applications like Physically Based Rendering (See PBRT (Physically Based Rendering: From Theory To Implementation), integral equations describing light scattering are solved numerically using Monte-Carlo Integration (MC).
MC Integration estimates the integral by a weighted mean of the operand evaluated at samples drawn from a given distribution. With n samples, it converges to the correct result at a rate of O(1/sqrt(n)). To halve the error, you need four times as many samples. Therefore, optimizing the sampling process to make the most of each sample is crucial.
Techniques like stratified sampling helps ensuring that all regions of the integrand are equally likely to be sampled, avoiding the redundancy of closely spaced samples that provide little additional information.
The mapping we discussed earlier is valid as it uniformly samples the unit disk. However, it distorts areas on the disk, particularly near the outer edge. Square regions of the unit square can be mapped to very thin and stretched areas on the disk.

This distortion is problematic because the sampling on the square loses its homogeneous distribution property. Close (u,v) samples can result in widely separated points on the disk, leading to increased variance. As a result, more samples are needed in the Monte Carlo integration to offset this variance.
In this section, we’ll introduce another uniform sampling technique that reduces distortion, thereby preventing unnecessary increases in variance.
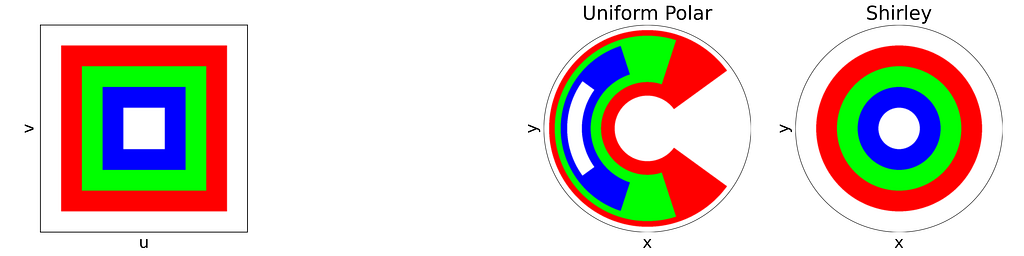
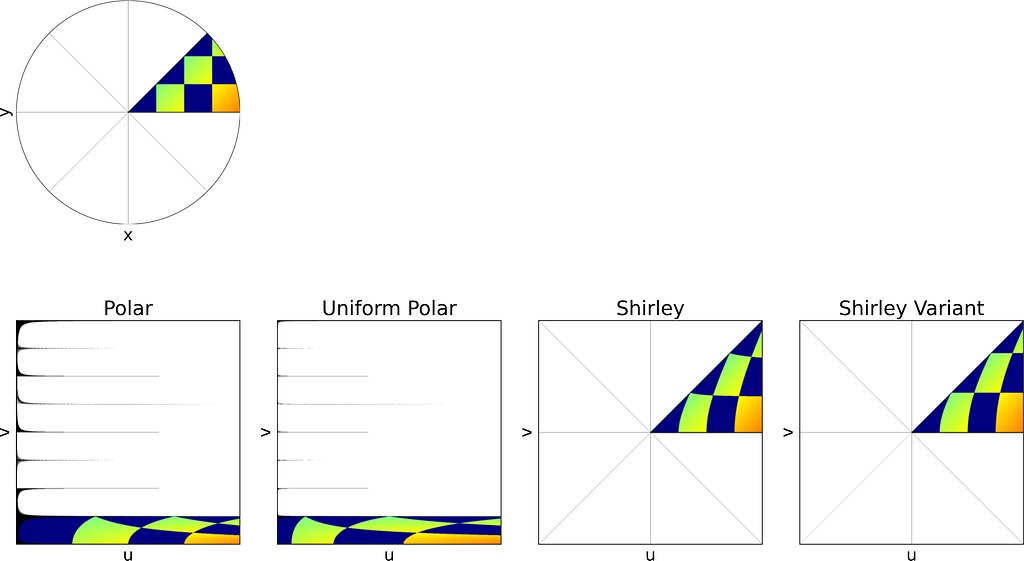
In 1997, Peter Shirley published “A Low Distortion Map Between Disk and Square”. Instead of treating the uniform unit square as a plain parameter space with no spatial meaning, as we did with the radius and angle, he suggests to slightly distort the unit square into the unit disk.
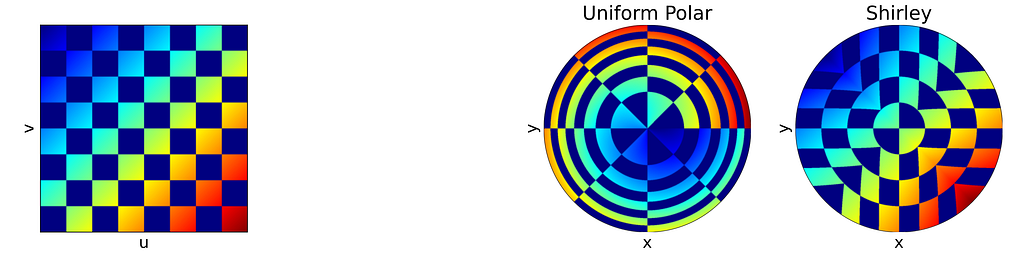
The idea is to map concentric squares within the unit square into concentric circles within the unit disk, as if pinching the corners to round out the square. In the figure below, this approach appears much more natural compared to uniform polar sampling.
The unit square is divided into eight triangles, with the mapping defined for one triangle and the others inferred by symmetry.

As mentioned at the beginning of the article, it is more convenient to switch between the [0,1]² and [-1,1]² definitions of the unit square rather than using cumbersome affine transformations in the equations. Thus, we will use the [-1,1]² unit square to align with the [-1,1]² unit disk definition.
As illustrated in the figure above, the reference triangle is defined by:
Mapping the vertical edges of concentric squares to concentric arc segments means that each point at a given abscissa u is mapped to the radius r=u. Next, we need to determine the angular mapping f that results in a uniform distribution across the unit disk.
We can deduce the determinant of the corresponding Jacobian.
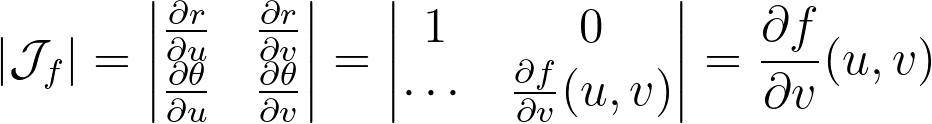
For a uniform disk distribution, the density within the eighth sector of the disk (corresponding to the reference triangle) is as follows.

On the other side, we have:
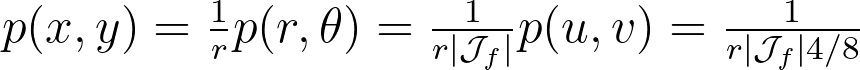
By combining the three previous equations and r=u , we get:
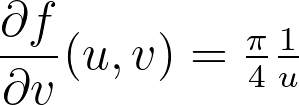
Integrating the previous equations with a zero constant to satisfy θ=0 when v=0 gives the angle mapping. Finally, we get the following mapping.
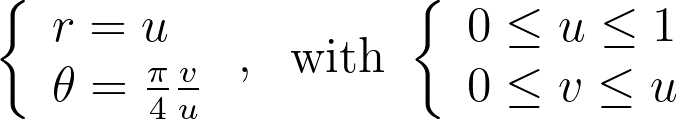
The seven others triangles are deduced by symmetry. The resulting distribution is effectively uniform, as confirmed by the empirical density map shown below.
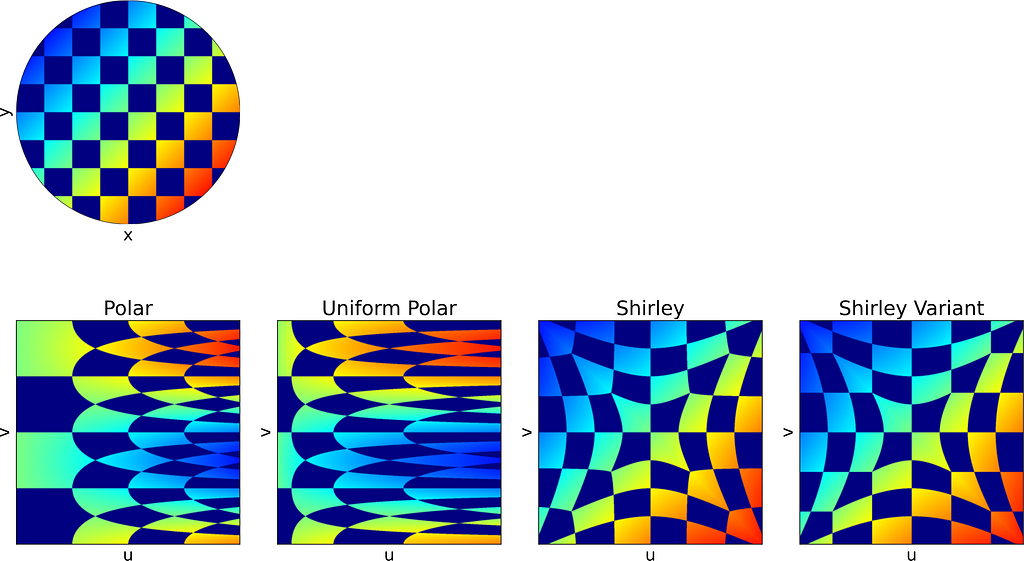
As expected, Shirley’s mapping, when applied to the colored grid, significantly reduces cell stretching and distortion compared to the polar mapping.
The θ mapping in Shirley’s method isn’t very intuitive. Thus, as seen in the figure below, it’s tempting to view it simply as a consequence of the more natural constraint that y depends solely on v, ensuring that horizontal lines remain horizontal.

However, this intuition is incorrect since the horizontal lines are actually slightly curved. The Shirley mapping presented above, i.e. the only uniform mapping respecting the r=u constraint, enforces the following y value, which subtly varies with u.
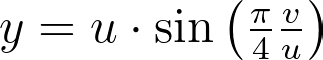
Although we know it won’t result in a uniform distribution, let’s explore a variant that uses a linear mapping between y and v, just for the sake of experimentation.
The Shirley variant shown here is intended solely for educational purposes, to illustrate how the Shirley mapping alters the horizontal lines by bending them.
We obtain y by scaling v by the length of the half-diagonal, which maps the top-right corner of the square to the edge of the disk. The value of x can then be deduced from y by using the radius constraint r=u.
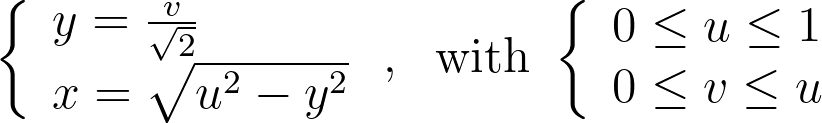
The figure below shows a side-by-side comparison of the original Shirley mapping and its variant. While both images appear almost identical, it’s worth noting that the variant preserves the horizontality of the lines.
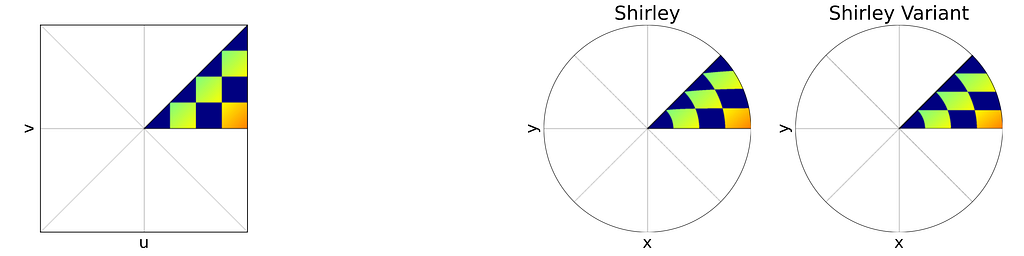
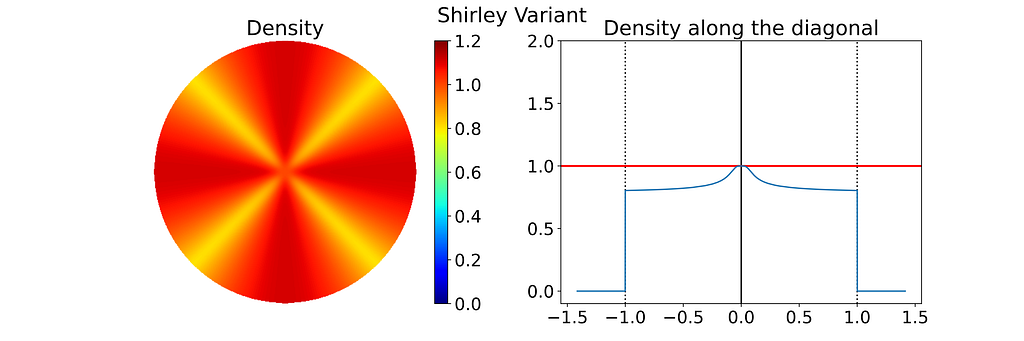
As expected, the empirical density map shows notable deviations from uniformity, oscillating between 0.8 and 1.1 rather than maintaining a constant value of 1.0.
Keep in mind that the density shown below depends on the angle, so the 1D density profile would vary if extracted from a different orientation.

In the second section of this article, visualizing how a square image is mapped to a disk proved helpful in understanding the distortion caused by the mappings.
To achieve that, we could naively project each colored pixel from the square onto its corresponding location on the disk. However, this approach is flawed, as it doesn’t ensure that every pixel on the disk will be assigned a color. Additionally, some disk pixels may receive multiple colors, resulting in them being overwritten and causing inaccuracies.
The correct approach is to reverse the process: iterate over the disk pixels, apply the inverse mapping to find the corresponding floating-point pixel in the square, and then estimate its color through interpolation. This can be done using cv2.remap from OpenCV.
Thus, the current mapping formulas only allow us to convert disk to square images. To map from square to disk, we need to reverse these formulas.
The inverse formulas are not detailed here for the sake of brevity.
Each of the following subsections will illustrate both the square-to-disk and disk-to-square mappings using a specific pattern image. Enjoy the exploration!

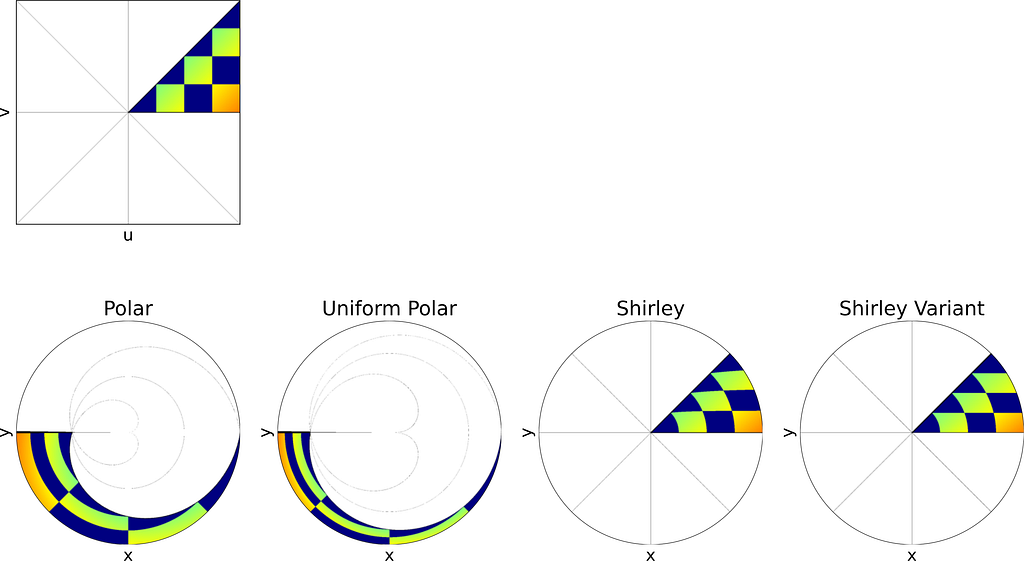

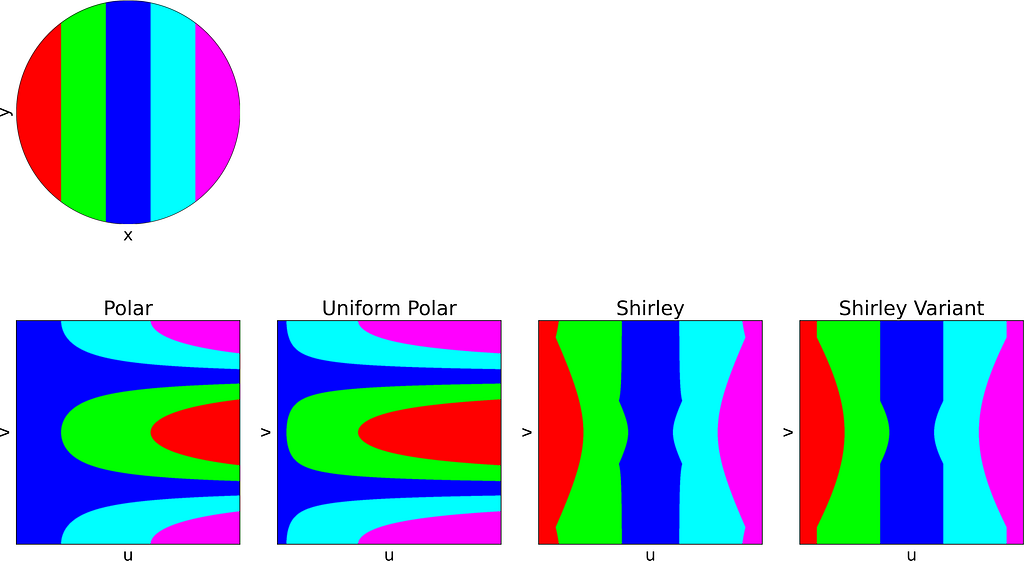

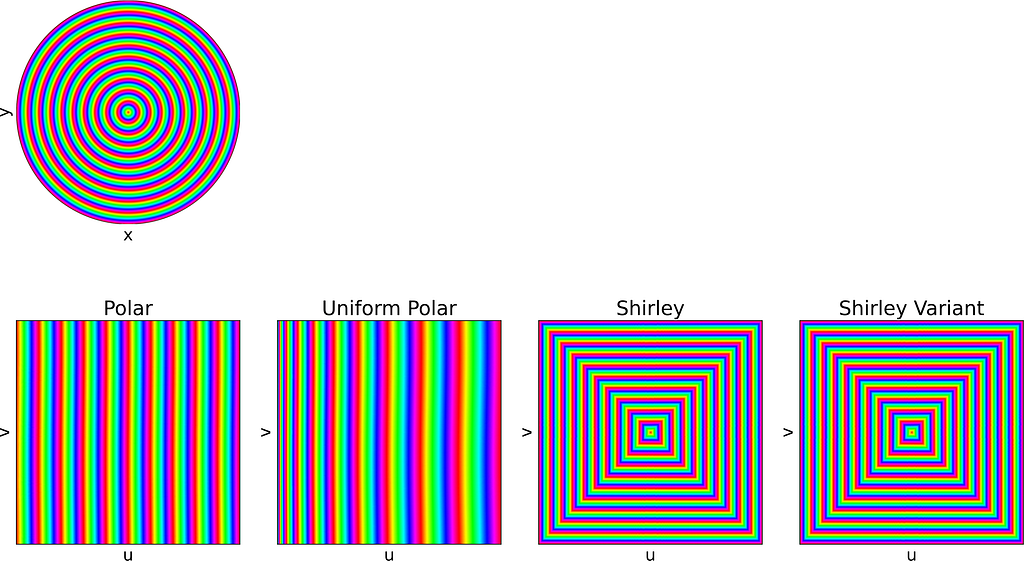
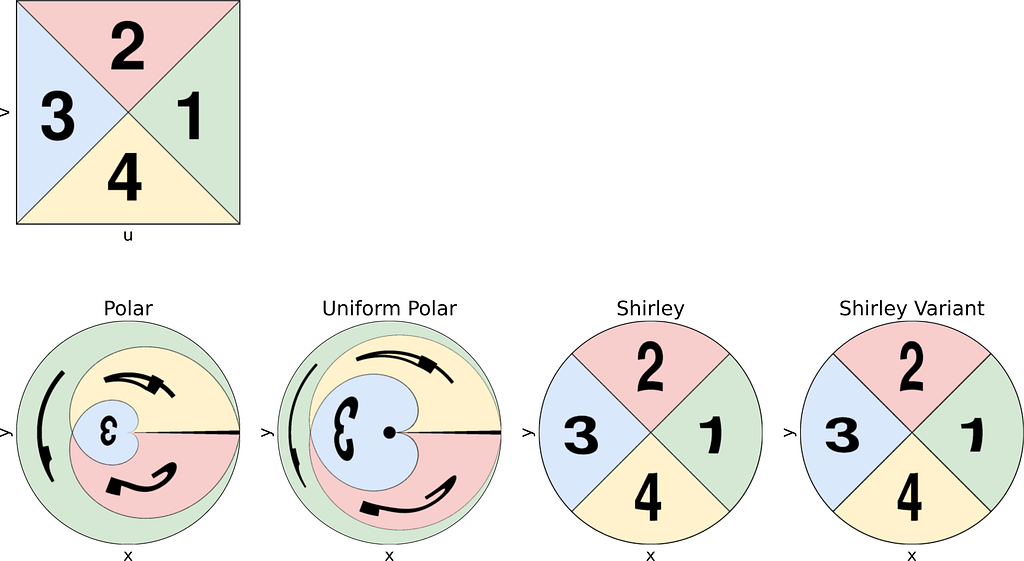




The naive disk sampling approach using uniform polar coordinates is a good example for understanding how transforming variables can affect their distribution.
Using the inversion method you can now turn a uniform sampling on [0,1] into any 1D distribution, by using its inverse Cumulative Distribution Function (CDF).
To sample any 2D distribution, we first sample a variable from its marginal density and then draw the second variable from its conditional density given the first variable.
Depending on your use-case, you might want to guarantee that nearby (u,v) samples will remain close when mapped onto the disk. In such cases, the Shirley transformation is preferable to uniform polar sampling, as it introduces less variance.
Unit Disk Uniform Sampling was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Unit Disk Uniform Sampling
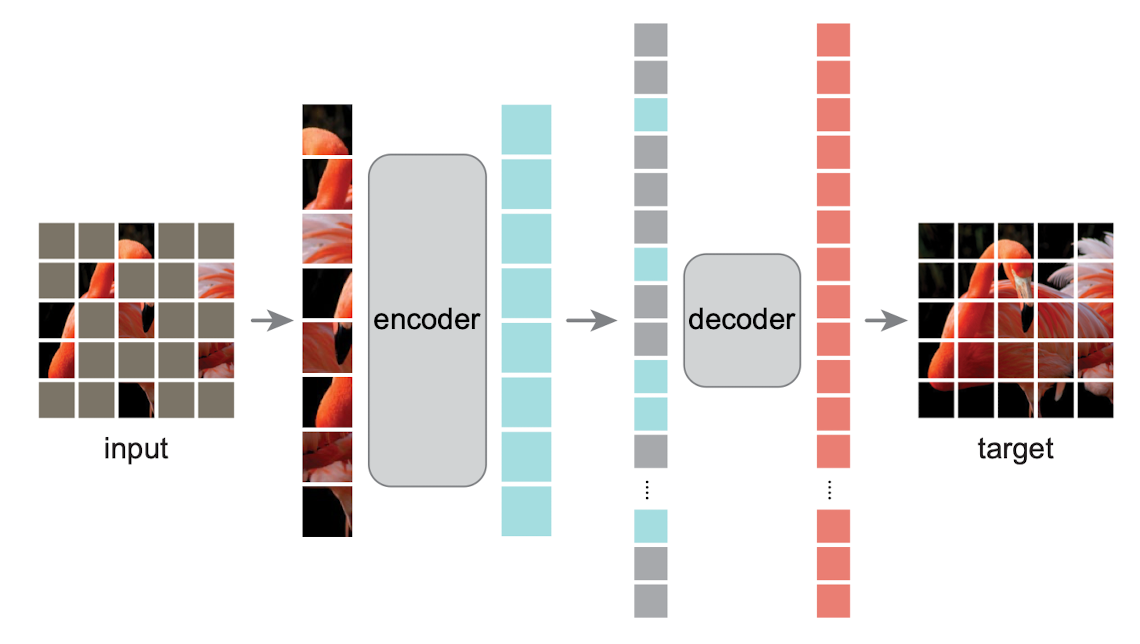

A Step-by-Step Guide to Building MAE with Vision Transformers
Originally appeared here:
How to Implement State-of-the-Art Masked AutoEncoders (MAE)
Go Here to Read this Fast! How to Implement State-of-the-Art Masked AutoEncoders (MAE)


This is part one of a series of articles, in which we will demystify data strategy — an essential component for any organization striving to become data-driven in order to stay competitive in today’s digital world. Use the cheat sheet provided in this article to kick-start your own data strategy development!
· 1. Motivation & Context
∘ 1.1 The Data-Driven Company
∘ 1.2 Where is the Challenge?
· 2. Is Data Not Already Handled Within the IT Strategy?
· 3. What Strategy Framework to Use for Designing a Data Strategy?
∘ 3.1 The Playing to Win Framework
∘ 3.2 Tool 1: The Strategy Process Map
∘ 3.3 Tool 2: The Strategy Choice Cascade
∘ 3.4 The Playing to Win Framework for Data Strategy Design
· 4. Link Between Data & Business Strategy
· 5. The Data Strategy Choice Cascade
∘ 5.1 Translating the Choice Cascade to Data & AI
∘ 5.2 The Data Strategy Choice Cascade
∘ 5.3 The Cheat Sheet for the Data Strategy Choice Cascade
∘ 5.4 When to Use the Data Strategy Choice Cascade
· 6. Two Example Data Strategies
· 7. Conclusions & Outlook
· References
Companies big or small, and independent of which industry they are playing in, strive to become data-driven. Regardless of what technology you use or how you name it — Data Science, Business Intelligence (BI), Advanced Analytics, Big Data, Machine Learning or (Generative) Artificial Intelligence (AI) — being data-driven is about leveraging data as a strategic company asset.
The big promises of being data-driven are:
This, in turn, leads to a long-term competitive edge through:
These benefits are realized through individual data uses cases. Some concrete examples are:
The benefits of becoming data-driven appear to be self-evident and there seems to be a general consent that for most companies there is no way around it. A quote translated from [1] nails it:
“Consistent value creation with data is already a decisive competitive advantage for companies today, and in the near future it will even be essential for survival.” [1]
If the general benefits of being data-driven are self-evident, where is the catch? Why is not every organization data-driven?
In fact, although the topic is not new — BI, Data Science and Machine Learning have been around for several decades — many companies still struggle to leverage their data and are far away of being data-driven. How is this possible?
To be clear from the start: From my perspective, the actual challenge was and still is rarely a matter of technology, even if so many technology providers like to claim exactly that. Sure, technology is the basis for making data-based decisions – as it is the basis for nearly every business-related activity nowadays. IT systems, tools and algorithms are readily available to execute data-based decision making. Equipping an organization with the right tools is a complicated, but not a complex problem [16], which can be adequately solved with the right knowledge or support. So, what does prevent organizations to continuously innovate, test and implement data use cases — like those above — to leverage data as a strategic asset?
In order to become data-driven, the way in which employees recognize, treat and use data within the daily business needs to radically change.
Being data-driven means, that people in every department must be able to translate critical business problems into analytical questions, which can then be addressed with data and analyses. There needs to be a (data) culture [3] within the organization, that ensures that employees want, can and must use data to improve their daily work. However, changing the behavior of a larger number of people is never a trivial task.
“Organizations need to transform to become data-driven.” [2]
So the real challenge is to sustainably change the way decisions are made in an organization. This cannot be accomplished, by designing and conducting a project, this requires a transformation.
Transforming an organization to become data-driven is a complex – not complicated – challenge for companies. This requires a solid strategic foundation — a data strategy.
However, many organizations do not posses a data strategy, struggle to create one or fear it is a lengthy process. With this article, we want to address this, by demystifying data strategy design and equipping the readers with the adequate tools to make their data strategies a success.
Most often organizations have a corporate strategy, an IT strategy or even a digital strategy. So, where is the need for a dedicated data strategy?
If your organization possesses any strategy, which addresses data as an asset with sufficient depth, you are fine. Sufficient depth means, that fundamental questions regarding data value creation are elaborated and answered, allowing the organization to take concrete actions to leverage data as an asset. However, in my experience, this is rarely the case, and there is often a lack of joint understanding in organizations, how the terms data, digital and technology differ and relate to each other.
Whilst digital strategies usually focus on process digitalization or the design of digital solutions for either internal staff or external customers, IT strategies often focus on system landscape, applications and network infrastructure. Both of them are closely related to generating and utilizing data, but neither digital nor IT strategy is — in its core — concerned with enabling an organization to become data-driven.
The info-graphic provides a more detailed comparison of the terms data, digital and technology:

Consequently, for each organization, it is important to first assess what data related topics are already covered by existing strategies, initiatives and corresponding leaders. Then, if existing strategies do not give a detailed answer to how the organization can leverage data as an asset, it is time to create a dedicated data strategy.
Strategy itself is perhaps one of the most misunderstood concepts [14]. There are many definitions and interpretations. As a consequence, there does not seem to be the one single true approach for designing a data strategy. So where to start?
What we propose here is to select a proven and generic framework, which can be used to develop (any kind of) strategy and apply this to data strategy design. For this, we use the “Playing to Win” (P2W) strategy framework [4], which originates from joint work of Alan G. Lafley, who was former CEO of P&G, and Roger Martin, who worked for Monitor Consulting when starting to develop the framework.
The approach became the standard strategy approach at P&G and has successfully been applied in many industries since. In addition, the P2W framework has constantly been complemented and refined by Roger through a series of Strategy Practitioner Insights [15,17].
The benefits of choosing the P2W approach above others are, that it is widely known and applied and comes with an entire ecosystem of processes, templates and trainings that can be leveraged for designing your data strategy.
In the P2W framework, strategy is defined as follows [4]:
“Strategy is an integrated set of choices that uniquely positions a firm in its industry so as to create sustainable advantage and superior value relative to the competition.” [4]
So strategy is all about choice, making these tough decisions that give you a competitive edge, with no bullet-proof certainty that the choices will turn out to be the right ones. Note, that this quite differs from declaring strategy being a kind of plan [9].
The P2W strategy framework boils down to two core tools for strategy design.
The Strategy Process Map is a set of steps guiding the strategy design process [5,6]. In essence, it helps to innovate several scenarios or so called possibilities for what your strategy might look like. These possibilities are subsequently evaluated and compared, so that the strategy team can choose the most promising possibility as final strategy.
It makes use of a rigorous evaluation methodology. This helps to create clarity for each possibility about the underlying assumptions that would have to be true, such that a possibility is considered to be a good strategy.
The Strategy Process Map consists of 7 phases and can be visualized as follows:

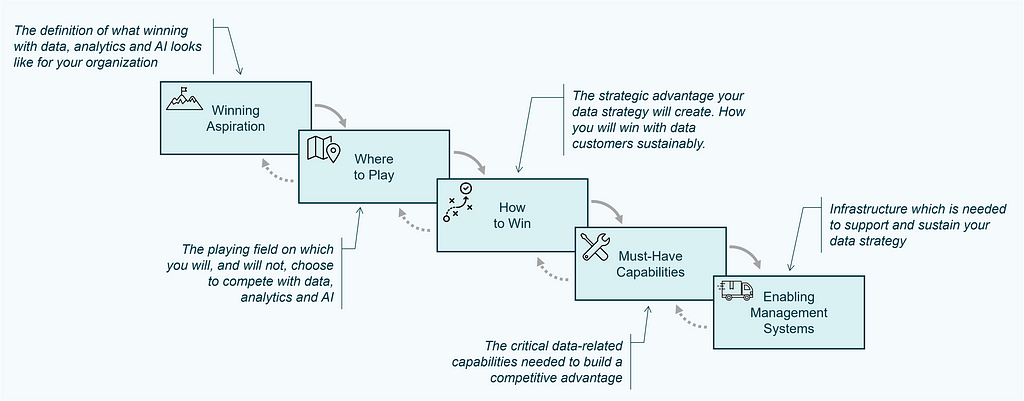
The Strategy Choice Cascade is the second tool that is used to document essential components of the strategy, which serves as output of the strategy work and is a nice way to visually communicate the strategy to stakeholders [7,8]. It consists of five elements and is often visualized similar to a waterfall:

These five elements of the Strategy Choice Cascade are defined as:
The actual heart of the strategy is made of the coherent choices made in box two and three: Where to Play & How to Win.
The boxes of the cascade each stand for a topic for which those tough choices, that we mentioned earlier have to be made.
How the cascade works is best illustrated using a real-world example, which is taken from [9] and describes choices for the corporate strategy of Southwest Airlines.

During the strategy design process, the Strategy Choice Cascade is not only filled once, but is repeatedly utilized at several phases of the Strategy Process Map. For example, every strategic possibility, which is created in the innovation phase, is described using the cascade to build a joint understanding within the strategy team. Also, the current strategy of the organization is described as a starting point for the strategy design process, in order to build a common understanding of the status-quo.
The P2W framework is not limited to the design of corporate strategies, but can be utilized to build any kind of strategy, e.g. for company divisions, functions (such as IT, Marketing or Sales) or even for individuals.
Consequently, it can also be utilized to design data strategies. So, what makes picking the P2W framework for designing a data strategy a particularly good choice?
Whilst the idea of applying the P2W framework for data strategy design is neither rocket science nor new, existing literature [e.g. 12,13] does — to the knowledge of the author — not provide a detailed description of how to adapt the framework for the application to data & AI strategy design in a straightforward manner.
In the remainder of this article, we therefore adopt the Strategy Choice Cascade to data strategy design, equipping data strategy design teams with the tools required to readily apply the P2W framework for their strategy work. This results in a clear definition of what a data strategy is, what it comprises and how it can be documented and communicated.
Applying Data Science, AI or any other data-related technology in a company is not an end in itself. Organizations do well not to start a potentially painful corporate transformation program to become data-driven without a clear business need (although I saw this happening more often than one would think). Hence, there must be a good reason why becoming data-driven is a good idea or even essential for the company to survive, before jumping into designing a data strategy. This is often described as a link between data and business strategy.
The great news is, when using the P2W framework for data strategy design, there are natural ways to provide such a link between data and business, by declaring data management, analytics or AI as must-have capabilities within the corporate strategy, enabling the organization to win.
One example for this can be found in [7], where the Strategy Choice Cascade is formulated for the corporate strategy of OŪRA. This health technology company produces a ring, which captures body data similar to a smart watch. The capabilities are, amongst others, defined as follows:

From this, the need for state-of-the-art data management and data analytics capabilities are apparent.
As the benefits for being data-driven exist in nearly every industry, data management, analytics or AI are nowadays not only must-have capabilities for high-tech companies, such as in the example above. Industries such as manufacturing, finance, energy & utilities, chemicals, logistics, retail and consumer goods increasingly leverage data & analytics to remain competitive.
In whatever industry your company plays, it ideally has already established the need for being data-driven and expressed it as part of the corporate strategy or any other strategy within the organization (e.g. sales or marketing), before you start with your data strategy work.
In many situations, however, such an explicit link between business and data is not given. In such cases, it is important to spend enough time, to identify the underlying business problem, which should be addressed by the data strategy. This is typically done in phase 1 of the Strategy Process Map (cf. Figure 2).
One way to identify the strategic target problem for the data strategy is peeling the onion by conducting a series of interviews with relevant business and management stakeholders. This allows to identify pains & gains — from a business perspective as well as with regards to the management and usage of data in the organization. Once this is done, it is then important to create a consent amongst stakeholders about the problem to be addressed. If there is consent that data is mission critical for the organization, the business need for a data strategy is evident and the corresponding corporate strategy should be updated accordingly.
Once we have established the need for the company to treat data as a valuable asset which needs to be taken care of and which needs to be leveraged, it is time to design a data strategy.
In order to apply the P2W framework to data strategy design, we first must translate the wording from the corporate context to the data context. So, we start by defining some core elements and rephrase them, where it seems helpful:
In addition, the strategy definition of the P2W framework can directly be augmented to data strategy:
Data Strategy is an integrated set of choices that uniquely positions a firm in its industry so as to create sustainable advantage and superior value relative to the competition, by leveraging data as an asset.
Once the core elements have been translated and we have defined what data strategy means to us, we can finally define the Data Strategy Choice Cascade:
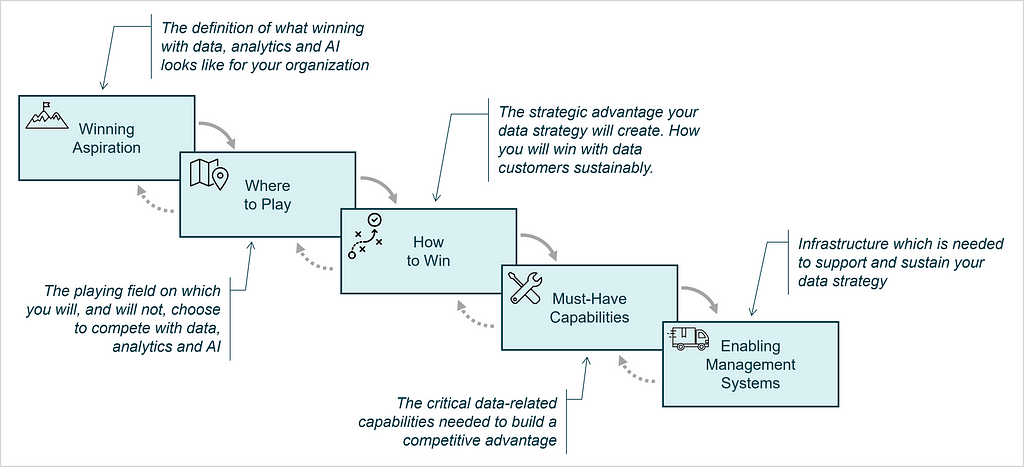
Some more detailed thoughts on data monetization options as part of the Where to Play for data strategies can be found in [11].
If data strategy is about making choices, what are these choices for each element of the Data Strategy Choice Cascade in detail? The following Cheat Sheet for the Data Strategy Choice Cascade compares and contrasts the cascade for corporate and data strategy in more detail and provides example choices to be made for the data strategy design.

Similar to the cascade for corporate strategy, the data strategy choice cascade can be applied in several situations, e.g. it can be utilized to:
In order to illustrate the application of Data Strategy Choice Cascade, we create two (fictitious) possibilities for the data strategy of the company OŪRA. Recall that OŪRA is a health technology company producing a ring, which captures body data similar to a smart watch. A corporate strategy formulation for this company using the P2W framework can be found in [7].
We consider two possibilities, which are quite different, in order to illustrate how the Data Strategy Choice Cascade can be utilized during the data strategy design process to uniformly document, effectively compare and communicate different strategy possibilities.
The first strategic possibility focuses on data-driven features for end-users as external data customers.

The second possibility focuses on analytics for operational excellence of internal data customers.

Note, that the organizational and technological choices are made in the the fifth element — Enabling Management Systems — that certainly depend on the core strategic choices made in the preceding elements. The choice cascade prevents users from falling into the common trap of jumping into technological solutions, before the actual strategy has been defined.
We have seen that the renowned and practice-proven Playing to Win framework for strategy design can be modified for data strategy development leading to the Data Strategy Choice Cascade. The cheat sheet provided can guide data strategy design teams to rapidly apply the framework for their strategy work. Consequently, when it comes to data strategy design, there is no need to re-invent the wheel, but you can stand on the shoulders of giants to ensure your data strategy becomes a success, allowing your company to win.
Is this all? Are we now set to develop our own data strategy?
The cascade is merely a tool, which is used to express many possibilities, that we create during the data strategy design process. If you just use the cascade to write down one possibility for your data strategy, which you think is a good idea, how do you know that this is the best option for your company to win with data?
To find out, you need to apply the Strategy Process Map for your data strategy design, which I will detail in one of my next articles.
[1] Sebastian Wernicke, Data Inspired (2024), book in German language published by Vahlen
[2] Caroline Carruthers and Peter Jackson, Data-Driven Business Transformation (2019), book published by Wiley
[3] Jens Linden, Datenkultur — Was & Warum? (2024), LinkedIn post
[4] A. G. Lafley and Roger L. Martin, Playing to Win (2013), book published by Harvard Business Review Press
[5] Michael Goitein, The “Playing to Win” Framework, Part II — The Strategy Process Map, blog
[6] IDEO U, Strategic Planning: How to Get Started, blog
[7] Michael Goitein, The “Playing to Win” Framework — Part III — The Strategy Choice Cascade, blog
[8] Roger Martin, Decoding the Strategy Choice Cascade (2023), Medium article
[9] Roger Martin, A Plan Is Not a Strategy (2022), video
[10] Jens Linden, Daten — Digital — Technologie: ist das alles das Gleiche? (2024), LinkedIn post
[11] Jens Linden, Datenmonetarisierung — Das Where to Play für Datenstrategien (2024), LinkedIn post
[12] Christena Antony, Beyond the Buzzwords: Crafting a Data Strategy that Works! (2024), LinkedIn article
[13] Deloitte & Google News Initiative, Digital transformation through data: a guide for news and media companies to drive value with data (2019), website
[14] Marc Sniukas, What the heck is strategy anyway? (2024), LinkedIn post
[15] Roger Martin, (Playing to Win) x 5 (2024), Medium article
[16] intrinsify Content Team, So unterscheiden moderne Manager: Komplex vs. Kompliziert (2023), website
[17] Roger Martin, Playing to Win/ Practitioner Insights (2024), website with list of articles
Unless otherwise noted, all images are by the author.
Side note: ChatGPT-4o was used to complement some elements of the cheat sheet example choices and the choices of the example data strategies to ensure anonymity.
The Data Strategy Choice Cascade was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
The Data Strategy Choice Cascade



I was recently asked to speak to a group of private equity investors about my career, what I have learned from it, and what opportunities I see because of those experiences.
Given my familiarity with data businesses, I chose to tie things together with a focus on them, particularly how to identify and evaluate them quickly.
Why data businesses? Because they can be phenomenal businesses with extremely high gross margins — as good or better than software-as-a-service (SaaS). Often data businesses can be the best businesses within the industries that they serve.
As a way to help crystalize my thinking on the subject and to provide a framework to help the investors separate the wheat from the chafe, I created a Data Business Evaluation Cheat Sheet.
For those yearning for a definition of data businesses, let’s purposefully keep it broad — say businesses that sell some form of data or information.
I broke out four evaluation criteria: Data Sources, Data Uses, Nice-to-Haves, and Business Models.
Each of those criteria have a variety of flavors, and, while the flavors are listed in the columns of the cheat sheet in order of the amount of value they typically create, it is important to say that many successful data businesses have been created based on each criterion, even the lower ranked criteria, or combinations thereof.

Data Sources:
How a data business produces the data that it sells is of critical importance to the value of the business, primarily in terms of building a moat versus competition and/or creating a meaningful point of differentiation.
Generally, the best source of data is proprietary data that the company intentionally produces via a costly to replicate process such as the TV broadcast capture network operated by Onclusive. Sometimes a company is lucky enough to produce this asset as a form of data exhaust from its core business operations such as salary data from Glassdoor. Data exhaust can be used to power another part of the same company that produces it, such as Amazon using purchase data to power its advertising business. Sometimes data exhaust is used to power a separate data business or businesses such as NCS which leverages register data from Catalina Marketing’s coupon business.
A close second in terms of a valuable data source are those businesses that benefit from a network effect when gathering data. Typically, there is a give-to-get structure in place where each data provider gets some valuable data in return for the data that it supplies. When the data that everyone gets benefits from the participation of each incremental participant, there is a network effect. TruthSet is an example of a company that runs a network effect empowered give-to-get model by gathering demographic data from data providers and returning to them ratings on the accuracy of their data.
Data aggregation can be a valuable way to assemble a data asset as well, but the value typically hinges on the difficulty of assembling the data…if it is too easy to do, others will do it as well and create price competition. Often the value comes in aggregating a long tail of data that is costly to do more than once either for the suppliers or a competitive aggregator. Equilar, for example, aggregates compensation data from innumerable corporate filings to create compensation benchmarking data. Interestingly, Equilar has used the data exhaust from its compensation data business which sells to H.R. departments, to create a relationship mapping business which sells to sales and marketing departments and deal oriented teams in financial service organizations.
Rounding out the set of key data sources are Data Enrichment and Data Analytics. Data enrichment creates value by enhancing another data source, sometimes by adding proprietary data, blending data with other data, structuring data, etc. Data Analytics companies make their mark by making sense of data from other sources often via insights that make mountains of data more digestible and actionable.
Data Uses:
When you can find a data set that is used between companies, it can be quite valuable because it is often difficult to displace. The best examples of this are when other companies trade value based on the data and the data fluctuates regularly. In this case, the data has become a currency. Examples of this include FICO scores from FICO or TV viewership data from Nielsen. In special occasions, data used between companies can also benefit from a network effect which tends to create value to the data provider. In fact, it can be the network effect that drives a data set to become a currency.
Data that is used to power workflows can also be very valuable, because moving away from it may require customers to change the way they work. The more frequent and the higher value the actions and decisions supported by the data, the better.
Typically, the more numerous the users of a data set within a customer and the more types of companies that can make use of the data, the more valuable it is. One way to evaluate this is to observe how easily and often a data set is combined with other data sets. Relatedly, some companies make a great business out of providing unique identifiers to enable data combinations such as Datavant which provides patient IDs to facilitate the exchange of healthcare data. Others, such as Dun & Bradstreet, use unique identifiers such as the DUNS Number, to support other parts of their business — credit reporting in this case.
Data Nice-to-Haves:
Data Nice-to-Haves are features of data businesses that typically do not sustain a data business on their own, but can significantly enhance the value of a data business. Benchmarks / Norms and Historical / Longitudinal data are typically attributes of data businesses that have been around for an extended period of time and can be difficult to replicate. The same goes for branded data though sometimes a brand can be extended to a new dataset once the brand is established — think J. D. Power applying its name to its acquisitions over the years.
Data Business Models:
The highest gross margin data businesses are generally those employing a syndicated business model in which they are selling the same set of data over and over again to different parties with no customization or with configuration that is handled automatically, preferably by the customer. The most stable data businesses tend to employ a subscription business model in which customers subscribe to a data set for an extended period of time. Subscriptions models are clearly better when the subscriptions are long term or, at least, auto-renewing.
Not surprisingly, the best data businesses are generally syndicated subscription models. On the other end, custom data businesses that produce data for clients in a one-off or project-based manner generally struggle to attain high margins and predictability, but can be solid businesses if the data manufacturing processes are optimized and they benefit from some of the other key data business attributes.
Financials:
The intent of this overview and associated cheat sheet are to analyze data business fundamentals, not to dig into typical financials. That said, typical healthy data businesses often have gross margins in the 65–75% range and EBITDA of 25–30%. Both of those number can be higher for exceptional businesses with the best of the characteristics above. Even in relatively slow growing industries, these businesses can trade at 15–18x EBITDA due to their resilience and the fact that they often require only modest R&D and marketing expense.
My parting thought to this group of investors, who were focused on a variety of verticals, was that though they may not consider themselves data business experts, they ought to be on the lookout for great data businesses in their areas of expertise. It is their detailed understanding of how their various industries work and what data their companies rely upon that will point them in the right direction and possibly uncover some data business gems for their partners who do invest in data businesses.
I’d like to thank several data business aficionados that helped inspire and refine my thinking on the subject: John Burbank, David Clark, Conor Flemming, Andrew Feigenson, Travis May, and Andrew Somosi. In particular, I’d recommend Travis’ related article, which was of particular inspiration to me, as additional reading on this subject.
Data Business Evaluation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Data Business Evaluation

During my studies, I attended a data science seminar and came into contact with the statistical programming language R for the first time. At the time, I was fascinated by the resulting potential uses. In the meantime, the statistical evaluation of data has become easier thanks to developments in the field of machine learning. Of course, a certain level of technical understanding is required, and you need to know what certain methods actually do. It is also necessary to know what data or input is required for certain methods to work at all or deliver meaningful results. In this article, I would like to discuss the development of a first version (V1) of a local app that can be used to automatically apply various statistical methods to any datasets. This is an open source project for educational and research purposes.
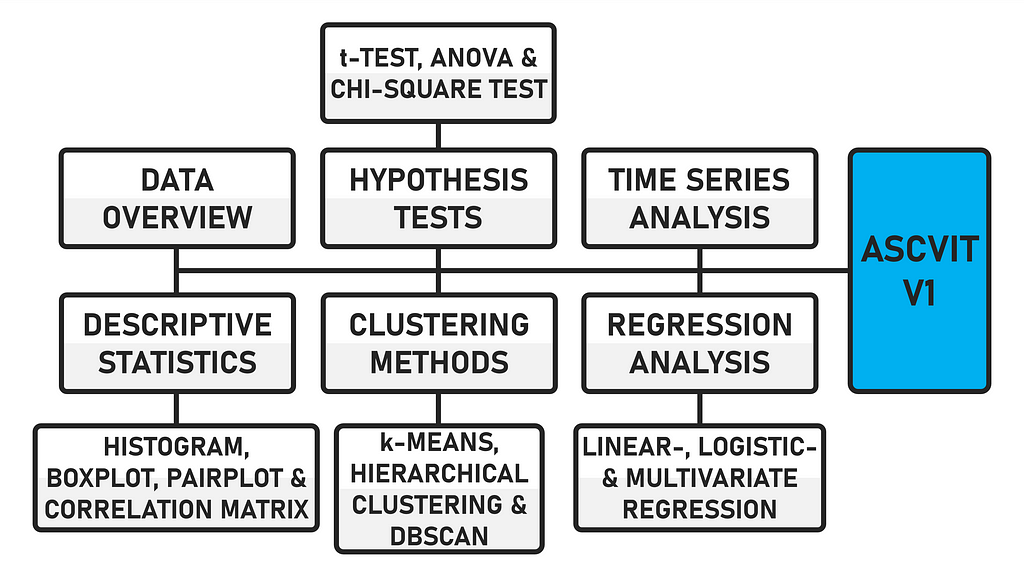
The data can be uploaded in either .csv or .xlsx format. The first version of the app provides a general data overview (data preview, data description, number of data points and categorization of variables), analyses in the field of descriptive statistics (histogram, boxplot, pairplot and correlation matrix), various hypothesis tests (t-test, ANOVA and chi-square test), regression analyses (linear, logistic and multivariate), time series analysis and supports various clustering methods (k-means, hierarchical and DBSCAN). The app is created using the Python framework Streamlit.

Due to the modular structure of the code, further statistical procedures can be easily implemented. The code is commented, which makes it easier to find your way around. When the app is executed, the interface looks like this after a dataset has been uploaded.

In addition to the automatic analysis in the various areas mentioned, a function has also been integrated that automatically analyses the statistically recorded values. The “query_llm_via_cli” function enables an exchange via CLI (command line interface) with an LLM using Ollama.
I have already explained this principle in an article published on Towards Data Science [1]. In the first version of the app, this functionality is only limited to the descriptive statistical analyses, but can also be transferred to the others. In concrete terms, this means that in addition to the automatic statistical calculation, the app also automatically interprets the data.

If you do not have your own data available, there are various sites on the internet that provide datasets free of charge. The dataset used for the development and testing of the app comes from Maven Analytics (License: ODC-BY) [2].

There are numerous free datasets on the site. The data I have examined deals with the sales figures of video games in the period from 1976 to 2024. Specifically, it is the sales figures from North America, Japan, the EU, Africa and the rest of the world. A total of 64016 titles and their rating, genre, console, etc. are recorded.
Unfortunately, not all information is available for all titles. There are many NaN (Not a Number) values that cause problems when analysed in Python or distort specific statistical analyses. I will briefly discuss the cleansing of data records below.

You can either clean the dataset before loading it into the app using a separate script, or you can perform the cleanup directly in the app. For the application in this article, I have implemented data cleansing directly in the app. If you want to clean up data records beforehand, you can do this using the following script.
import pandas as pd
df = pd.read_csv('YOUR .CSV FILE')
df_cleaned = df.dropna()
df_cleaned.to_csv('cleaned_file.csv', index=False)
print("Lines with missing data have been removed and saved in 'cleaned_file.csv'.")
The file is read using “pd.read_csv(‘.csv’)” and the data is saved in the DataFrame “df”. df.dropna()” removes all lines in the DataFrame that contain missing values ‘NaN’. The cleaned DataFrame is then saved in the variable “df_cleaned”. The data is saved in a new .csv file using “df_cleaned.to_csv(‘cleaned_file.csv’, index=False)”. Line indices are not saved. This is followed by an output for the successfully completed process “print(…)”. The code for this dataset cleanup can be found in the file “clean.py” and can also be downloaded later. Next, let’s move on to the actual code of the app.

To use the app, various libraries and modules are required, which in combination perform data visualization, statistical analysis and machine learning tasks.
import re
import subprocess
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
from matplotlib.patches import Patch
from scipy import stats
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression, LogisticRegression
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import streamlit as st
A note regarding the representation of the diagrams. Some use “pyplot” (Matplotlib) and others use “plotly” (e.g. Boxplot). Even if the use of “plotly” leads to more interactive graphics, it does not make sense to use it for every type of diagram. Ultimately, the user must decide individually how the diagrams should be displayed. The code must be adapted accordingly.
The required libraries for the application can be installed using the requirements.txt file in the ZIP directory with the following command.
pip install -r requirements.txt
The function “display_data_info()” specifically analyses the Pandas DataFrame “df” and outputs statistical key figures (mean value, standard deviation, etc.) “df.describe()”. The total number of data points (rows) of the DataFrame is output “len(df)”. Likewise, the numerical “numerical_columns” and categorical “categorical_columns” (strings) variables of the DataFrame.

The dataset has a total of 64016 data points and 6 numerical and 8 categorical variables. Before you start with certain statistical procedures, you should first look at the data. In the “Data overview” section, you can obtain various information to draw conclusions whether certain tests can be carried out at all.
For example, if there is no date variable in the dataset, no time series analysis can be carried out. If there is no binary variable, no logistic regression can be carried out. The app is already designed to ask for certain variable categories or to display error messages if incorrect values are transmitted. Next, let’s move on to descriptive statistics.
def display_data_info(df):
st.write("**Data description:**")
st.write(df.describe())
st.write(f"**Number of data points:** {len(df)}")
numerical_columns = df.select_dtypes(include=np.number).columns.tolist()
categorical_columns = df.select_dtypes(include='object').columns.tolist()
st.write("**Numerical variables:** ", ", ".join(numerical_columns))
st.write("**Categorical variables:** ", ", ".join(categorical_columns))
return numerical_columns, categorical_columns
The “descriptive_statistics()” function allows the user to select different chart types (histogram, boxplot, pairplot and correlation matrix). A brief explanation of the type follows via “st.markdown(”“”…“”“)”. One or more numerical variables must then be selected “selected_vars”. The option whether logarithmic scaling “apply_log_scale” should be applied is available, except for the correlation matrix. Applying logarithmic scaling to a variable is particularly useful if the data is heavily distorted. The visualization is created using the corresponding diagram function.
def descriptive_statistics(df, numerical_columns):
chart_type = st.selectbox("Select the diagram:", ["Histogram", "Boxplot", "Pairplot", "Correlation matrix"])
if chart_type == "Histogram":
st.markdown("""
**Histogram:**
A histogram shows the distribution of a numerical variable. It helps to
recognize how frequently certain values occur in the data and whether there are patterns, such as a normal distribution.
""")
elif chart_type == "Boxplot":
st.markdown("""
**Boxplot:**
A boxplot shows the distribution of a numerical variable through its quartiles.
It helps to identify outliers and visualize the dispersion of the data.
""")
elif chart_type == "Pairplot":
st.markdown("""
**Pairplot:**
A pairplot shows the relationships between different numerical variables through scatterplots.
It helps to identify possible relationships between variables.
""")
elif chart_type == "Correlation matrix":
st.markdown("""
*Correlation matrix:**
The correlation matrix shows the linear relationships between numerical variables.
A positive correlation indicates that high values in one variable also correlate with high values in another.
""")
if chart_type in ["Pairplot", "Correlation matrix"]:
selected_vars = st.multiselect("Select variables:", numerical_columns, default=numerical_columns)
else:
selected_vars = [st.selectbox("Select a variable:", numerical_columns)]
if chart_type != "Correlation matrix":
apply_log_scale = st.checkbox("Apply logarithmic scaling?", value=False)
else:
apply_log_scale = False
if st.button("Create diagram"):
if chart_type == "Histogram":
plot_histogram(df, selected_vars[0], apply_log_scale)
elif chart_type == "Boxplot":
plot_boxplot(df, selected_vars[0], apply_log_scale)
elif chart_type == "Pairplot":
plot_pairplot(df, selected_vars)
elif chart_type == "Correlation matrix":
plot_correlation_matrix(df, selected_vars)
The “plot_histogram()” function is used to create the histogram depending on the variable selected by the user. At the beginning, all NaN values are removed from the variable “cleaned_data”. Various statistical key figures (mean value “mean_value”, median “median_value”, standard deviation “std_value”, minimum “min_value” and maximum “max_value” and the upper and lower end of the standard deviation) are calculated.
Since the data is interpreted by an LLM, as mentioned at the beginning, the dispersion (standard deviation in relation to the range of the data) and distribution (difference between mean and median) of the data is classified. The histogram is created “fix, ax = plt.subplots()”, vertical lines are added to increase the informative value and finally the histogram is displayed “st.pyplot(fig)”. In the case of distorted or exponential data, logarithmic scaling can be activated, whereupon the y-axis of the histogram is adjusted. The graph then looks as follows [3].

As there are no models that can read out graphics directly, we create a universal context for the analysis by the LLM. The context contains the results of the statistical calculation and additional instructions or the desired interpretation. This means that the context, which serves as input for the LLM, can be applied to any dataset.
Specifically, the input includes the aforementioned statistical key figures, an analysis of the distribution (symmetrical, right-skewed or left-skewed), an estimate of the spread (low, moderate or high) and an interpretation formatted for the LLM. Depending on the desired output, the context can be individually adapted and further specified.

The analysis is sent to the LLM “response = query_llm_via_cli(context)”, whereupon an interpretation of the histogram takes place after a short time interval, depending on the performance of the local system “st.write(f”**Histogram Interpretation:** {response}”)”.
def plot_histogram(df, variable, apply_log_scale):
cleaned_data = df[variable].dropna()
mean_value = cleaned_data.mean()
median_value = cleaned_data.median()
std_value = cleaned_data.std()
min_value = cleaned_data.min()
max_value = cleaned_data.max()
std_upper = mean_value + std_value
std_lower = max(0, mean_value - std_value)
concentration_range = (mean_value - std_value, mean_value + std_value)
if std_value < (max_value - min_value) / 6:
scatter = "low"
elif std_value < (max_value - min_value) / 3:
scatter = "moderate"
else:
scatter = "high"
if abs(mean_value - median_value) < 0.1 * std_value:
distribution = "symmetrical"
elif mean_value > median_value:
distribution = "right-skewed"
else:
distribution = "left-skewed"
fig, ax = plt.subplots()
ax.hist(cleaned_data, bins=30, edgecolor='black', alpha=0.7)
ax.axvline(mean_value, color='red', linestyle='--', label=f'Mean: {mean_value:.2f}')
ax.axvline(median_value, color='green', linestyle='-', label=f'Median: {median_value:.2f}')
ax.axvline(std_upper, color='blue', linestyle=':', label=f'+1 Std: {std_upper:.2f}')
ax.axvline(std_lower, color='blue', linestyle=':', label=f'-1 Std: {std_lower:.2f}')
ax.set_title(f"Histogram of {variable}")
ax.legend(title=f'Std-Deviation: {std_value:.2f}')
if apply_log_scale:
ax.set_yscale('log')
st.pyplot(fig)
context = (
f"Here is an analysis of the distribution of the variable '{variable}':n"
f"- Mean: {mean_value:.2f}n"
f"- Median: {median_value:.2f}n"
f"- Standard deviation: {std_value:.2f}n"
f"- Minimum: {min_value:.2f}n"
f"- Maximum: {max_value:.2f}nn"
f"The distribution of the data shows a {distribution} distribution.n"
f"The small difference between mean and median indicates a {distribution} distribution.n"
f"A strong concentration of data points is observed between {concentration_range[0]:.2f} and {concentration_range[1]:.2f}.n"
f"The scatter of the data is described as {scatter}, indicating a relatively tight distribution around the mean.nn"
f"Please analyze this distribution in the histogram, paying particular attention to symmetry, scatter, and potential deviations.n"
f"Avoid calling the distribution normal unless there are explicit indications.n"
f"Use only the names of the variables {variable} in the analysis!"
)
response = query_llm_via_cli(context)
st.write(f"**Histogram Interpretation:** {response}")
The “plot_boxplot()” function creates a boxplot for a variable selected by the user. Statistical key figures are calculated from the DataFrame based on the variable in order to display the distribution of the data in the diagram and to enable an analysis of the central tendency and dispersion using an LLM. In addition to the mean value, the median and the standard deviation, as with the histogram, the lower “q1”, upper “q3”, the interquartile range “iqr” (Q3 — Q1) and the lower or upper whisker “lower_whisker” and “upper_whisker”, which are based on the interquartile range (1.5 * IQR), are also determined for the boxplot.
The latter plays a role in identifying outliers and the other parameters where data is above or below a certain value. The boxplot is created using the Plotly library “fig = px.box(df, y=variable)” and finally displayed in the app “st.plotly_chart(fig)”. Logarithmic scaling can also be used for this chart type [4]. The chart then looks as follows:

As with the histogram, a context is also created for the boxplot, which is forwarded to the LLM. The statistical key figures are transmitted as well as information about potential outliers that lie outside the whisker values. The text sent to the LLM is formatted so that the analysis is performed on these metrics.
def plot_boxplot(df, variable, apply_log_scale):
mean_value = df[variable].mean()
median_value = df[variable].median()
std_value = df[variable].std()
q1 = df[variable].quantile(0.25)
q3 = df[variable].quantile(0.75)
iqr = q3 - q1
lower_whisker = max(df[variable].min(), q1 - 1.5 * iqr)
upper_whisker = min(df[variable].max(), q3 + 1.5 * iqr)
fig = px.box(df, y=variable)
fig.update_layout(title=f"Boxplot of {variable}")
if apply_log_scale:
fig.update_yaxes(type="log")
st.plotly_chart(fig)
context = (
f"Here is an analysis of the distribution of the variable '{variable}' based on a boxplot:n"
f"- Mean: {mean_value:.2f}n"
f"- Median: {median_value:.2f}n"
f"- Standard deviation: {std_value:.2f}n"
f"- Lower quartile (Q1): {q1:.2f}n"
f"- Upper quartile (Q3): {q3:.2f}n"
f"- Interquartile range (IQR): {iqr:.2f}n"
f"- Potential outliers outside values from {lower_whisker:.2f} to {upper_whisker:.2f}.n"
f"Please analyze this distribution and identify patterns or outliers.n"
f"Use only the names of the variables {variable} in the analysis!"
)
response = query_llm_via_cli(context)
st.write(f"**Boxplot Interpretation:** {response}")
The “plot_pairplot()” function creates a pairplot based on the variables selected by the user. If less than two variables are selected, an error message is displayed. Scatter plots for all possible combinations of the variables and a linear regression line are displayed to show the relationships between the variables. For this to work, the regression statistics are calculated for all possible pairs of the selected variables using the “calculate_regression_stats” function. The NaN values are removed from the selected variables “selected_vars”.
A linear regression is performed between the two variables. Here, “var1” is the independent variable x and “var2” is the dependent variable y. The slope and the R2 value “r_squared” are calculated. The results are returned as a list of tuples (var1, var2, slope, r_squared). If three variables are selected [“A”, “B”, “C”], the function will calculate the regression statistics for the pairs (A, B), (A, C), (B, A), (B, C), etc. [5].
def calculate_regression_stats(df, selected_vars):
regression_results = []
for var1 in selected_vars:
for var2 in selected_vars:
if var1 != var2:
non_nan_data = df[[var1, var2]].dropna()
X = non_nan_data[[var1]].values.reshape(-1, 1)
y = non_nan_data[var2].values
if len(X) > 0 and len(y) > 0:
model = LinearRegression()
model.fit(X, y)
r_squared = model.score(X, y)
slope = model.coef_[0]
regression_results.append((var1, var2, slope, r_squared))
return regression_results
def plot_pairplot(df, selected_vars):
if len(selected_vars) > 1:
st.write("**Pairplot with regression lines:**")
pairplot_fig = sns.pairplot(df[selected_vars], kind='reg', diag_kind='kde',
plot_kws={'line_kws': {'color': 'red'}, 'scatter_kws': {'color': 'blue'}})
st.pyplot(pairplot_fig.fig)
corr_matrix = df[selected_vars].corr()
regression_stats = calculate_regression_stats(df, selected_vars)
correlation_list = "n".join(
[f"The correlation between {var1} and {var2} is {corr_matrix.at[var1, var2]:.2f}."
for var1 in corr_matrix.columns for var2 in corr_matrix.columns if var1 != var2]
)
regression_list = "n".join(
[f"The regression line for {var1} and {var2} has a slope of {slope:.2f} and an R² of {r_squared:.2f}."
for var1, var2, slope, r_squared in regression_stats]
)
context = (
f"Here are the correlation and regression analyses between the selected variables:n"
f"{correlation_list}nn"
f"{regression_list}nn"
f"Please analyze these relationships in detail based solely on the numerical values (correlation and regression lines).n"
f"Use only the names of the variables {selected_vars} in the analysis!"
)
response = query_llm_via_cli(context)
st.write(f"**Pairplot Interpretation:** {response}")
else:
st.error("At least two variables must be selected for a pairplot.")
KDE (Kernel Density Estimation) is used in the “plot_pairplot()” function for the diagonal to display the distribution of each individual variable. As with the previous functions, a context is again created for the analysis by the LLM. For this type of diagram, the LLM receives the data from the correlation and regression analysis. The text is formatted in such a way that a detailed interpretation of the relationship between the variables is generated.

The “plot_correlation_matrix” function is used to create a correlation matrix based on the variables selected by the user “if len(selected_vars) > 1”. If only one variable is selected, an error message is displayed. The visualization is done as a heatmap. The cells of the matrix are colored to show the strength and direction of the correlation. Correlations that are significant are automatically sent to the LLM for further analysis “if var1 != var2 and abs(corr_matrix.at[var1, var2]) >= 0.5”.
The linear correlation between the selected variables is displayed as the correlation coefficient (value between -1 and +1) “corr_matrix = df[selected_vars].cor()”. With a value of 0, there is no linear correlation. A value close to -1 indicates a strong negative correlation and a value close to +1 indicates a strong positive correlation. The pairs of variables and their correlation values are saved in “high_correlations” [4].

A context is created for the LLM. The existing significant correlations are classified for the textual description “correlation_list”. A strong correlation (positive or negative) is present with a value greater than 0.7. If the value is between 0.5 and 0.7, there is a moderate correlation and if the value is only just above 0.5, the correlation is weak. If no significant correlations were found, a corresponding message is displayed.
def plot_correlation_matrix(df, selected_vars):
if len(selected_vars) > 1:
corr_matrix = df[selected_vars].corr()
fig, ax = plt.subplots()
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', ax=ax)
ax.set_title("Correlation Matrix")
st.pyplot(fig)
high_correlations = []
for var1 in corr_matrix.columns:
for var2 in corr_matrix.columns:
if var1 != var2 and abs(corr_matrix.at[var1, var2]) >= 0.5:
if (var2, var1) not in [(v1, v2) for v1, v2, _ in high_correlations]:
high_correlations.append((var1, var2, corr_matrix.at[var1, var2]))
if high_correlations:
correlation_list = "n".join([f"- {var1} and {var2} have a correlation value of {value:.2f}, "
f"indicating a {'strong' if abs(value) > 0.7 else 'moderate' if abs(value) > 0.5 else 'weak'} correlation."
for var1, var2, value in high_correlations])
context = (
f"Here is an analysis of the significant correlations between the selected variables in the correlation matrix:n"
f"{correlation_list}nn"
f"Please analyze the correlations solely based on their strength and significance.n"
f"Use only the names of the variables {selected_vars} in the analysis!"
f"Focus in detail on the statistical relationship and patterns."
)
response = query_llm_via_cli(context)
st.write(f"**Model Response:** {response}")
else:
st.write("**No significant correlations were found.**")
else:
st.write("**The correlation matrix cannot be displayed because fewer than two variables were selected.**")
In the following statistical procedures, the interpretation of the respective key figures recorded by an LLM is not available. However, based on the previous procedure, independent implementation should not be a problem. Let us now turn to the various hypothesis tests.
In the current version, three different tests (t-test, ANOVA and chi-square test) can be carried out “test_type = st.selectbox()”. Depending on the test selected, a brief explanation of its purpose appears. Depending on the area of application, this description can be expanded or removed. The t-test is used to compare the mean values of two groups. The analysis of variance (ANOVA) compares the mean value of more than two groups. The chi-square test tests the independence between two categorical variables. Depending on which test is selected, the corresponding function is performed.
If the user has opted for the t-test, they must select a group variable (categorical) “group_col” and a value variable (numerical) “value_col”. The group variable defines the two groups to be compared. The value variable compares the mean value between the two groups. Once the selection has been made, the names of the two groups “group1” and “group2” must be entered in a text field “st.text_input()”. The two groups should appear in the selected categorical variable. The logarithmic scaling “apply_log_scale”, which is applied to the value variable, is also available here. When the test is performed, the data of the groups is extracted and the number of data points (after the NaN values have been removed) is output. The t-statistic and the p-value are displayed.
The first value indicates the difference in the mean values between the two groups relative to the spread of the data. Whether the difference between the groups is statistically significant is indicated by the p-value. If it is less than 0.05, it is significant. To visually highlight the distribution of the two groups “filtered_df = df[df[group_col].isin([group1, group2])]”, a boxplot is created “fig, ax = plt.subplots()”. Here “pyplot” is used, alternatively you can also use “plotly” [6].

In this example, “genre” was selected as the group variable and “critic_score” as the value variable. Action (group 1) and Shooter (group 2) were defined as groups. The function also calculates whether there are significant outliers in the groups. An outlier is defined as a data point exceeding the upper quartile by more than 1.5 times the interquartile range “outliers_group1/2”. Finally, the outliers found are displayed to confirm the validity of the t-test. If the distortion is too large, this must be taken into account accordingly in order to better classify the reliability and interpretability of the test results.
def t_test(df, numerical_columns, categorical_columns):
group_col = st.selectbox("Choose the group variable:", categorical_columns)
value_col = st.selectbox("Choose the value variable:", numerical_columns)
group1 = st.text_input("Name of group 1:")
group2 = st.text_input("Name of group 2:")
apply_log_scale = st.checkbox("Apply logarithmic scaling?", value=False)
if st.button("Perform t-Test"):
group1_data = df[df[group_col] == group1][value_col]
group2_data = df[df[group_col] == group2][value_col]
initial_count_group1 = len(group1_data)
initial_count_group2 = len(group2_data)
group1_data = group1_data.dropna()
group2_data = group2_data.dropna()
remaining_count_group1 = len(group1_data)
remaining_count_group2 = len(group2_data)
st.write(f"**Group 1 ({group1}):** Total number of data points: {initial_count_group1}, without NaN: {remaining_count_group1}")
st.write(f"**Group 2 ({group2}):** Total number of data points: {initial_count_group2}, without NaN: {remaining_count_group2}")
if apply_log_scale:
group1_data = np.log1p(group1_data)
group2_data = np.log1p(group2_data)
if not group1_data.empty and not group2_data.empty:
t_stat, p_value = stats.ttest_ind(group1_data, group2_data)
st.markdown(f"**t-Statistic:** {t_stat}")
st.markdown(f"**p-Value:** {p_value}")
filtered_df = df[df[group_col].isin([group1, group2])]
fig, ax = plt.subplots()
sns.boxplot(x=filtered_df[group_col], y=filtered_df[value_col], ax=ax, palette="Set2")
ax.set_title(f"Boxplot for {group1} vs. {group2}")
if apply_log_scale:
ax.set_yscale('log')
st.pyplot(fig)
outliers_group1 = group1_data[group1_data > group1_data.quantile(0.75) + 1.5 * (group1_data.quantile(0.75) - group1_data.quantile(0.25))]
outliers_group2 = group2_data[group2_data > group2_data.quantile(0.75) + 1.5 * (group2_data.quantile(0.75) - group2_data.quantile(0.25))]
st.write("**Outlier Analysis:**")
if not outliers_group1.empty:
st.write(f"In group 1 ({group1}) there are {len(outliers_group1)} outliers.")
else:
st.write(f"In group 1 ({group1}) there are no significant outliers.")
if not outliers_group2.empty:
st.write(f"In group 2 ({group2}) there are {len(outliers_group2)} outliers.")
else:
st.write(f"In group 2 ({group2}) there are no significant outliers.")
else:
st.error("One or both groups contain no data after removing NaN values.")
The “anova_test()” function integrates the option of performing an ANOVA test. This test checks whether there are significant differences in the mean values of several groups. The data is first cleaned “df_clean”. If the ANOVA test is significant, a Tukey’s HSD test (Honestly Significant Difference) is also carried out. At the beginning, a group variable and a value variable are again defined. If a group has fewer than 2 data points, it is excluded “valid_groups = group_sizes[group_sizes >= 2].index”.
If less than two groups remain after the adjustment, an error message is displayed and the test is not performed. The ANOVA test calculates the F-value and the p-value. The variability between the groups compared to the variability within the group is measured by the F-value. Whether the difference between the mean values of the group is significant is indicated by the p-value. If the value is less than 0.05, at least one group is significantly different. To visualize the results, a boxplot is created using “pyplot” [7].

If the ANOVA test produces significant results, a Tukey’s test is carried out to examine the differences between the individual group pairs in concrete terms. The ANOVA test therefore does not show which groups differ from each other. A diagram is created that shows the pairwise mean differences between the groups and their confidence interval “st.pyplot(tukey.plot_simultaneous())”.

Below the diagram, the results are displayed in a table “st.dataframe(tukey_results_df, height=400)”. The table contains the two groups, the mean difference “meandiff”, the adjusted p-value “p-adj”, the confidence interval and whether the null hypothesis can be rejected or not “reject” (True = significant, Fals = not significant). A brief example of the confidence interval. For the 3DS and GBA consoles, the interval lies between -0.9319 and -0.0061 and is therefore completely below zero. The difference in the mean value is significant.
The key figures can be used to have the results interpreted by an LLM. There is also an option to download the data as a .csv file for further statistical analyses (e.g. regression analyses) [7].
def anova_test(df, numerical_columns, categorical_columns):
group_col = st.selectbox("Choose the group variable:", categorical_columns)
value_col = st.selectbox("Choose the value variable:", numerical_columns)
if st.button("Perform ANOVA"):
df_clean = df[[group_col, value_col]].dropna()
group_sizes = df_clean.groupby(group_col).size()
valid_groups = group_sizes[group_sizes >= 2].index
df_filtered = df_clean[df_clean[group_col].isin(valid_groups)]
if len(valid_groups) < 2:
st.error("After removing small groups, there are not enough groups left for the ANOVA test.")
else:
grouped_data = [group[value_col].values for name, group in df_filtered.groupby(group_col)]
try:
anova_result = stats.f_oneway(*grouped_data)
st.markdown(f"**F-Value:** {anova_result.statistic}")
st.markdown(f"**p-Value:** {anova_result.pvalue}")
fig, ax = plt.subplots(figsize=(10, 6))
sns.boxplot(x=group_col, y=value_col, data=df_filtered, ax=ax)
plt.xticks(rotation=90)
st.pyplot(fig)
if anova_result.pvalue < 0.05:
st.write("The ANOVA test is significant. Tukey's HSD test will be performed.")
try:
tukey = pairwise_tukeyhsd(endog=df_filtered[value_col], groups=df_filtered[group_col], alpha=0.05)
st.pyplot(tukey.plot_simultaneous())
tukey_results_df = pd.DataFrame(data=tukey.summary().data[1:], columns=tukey.summary().data[0])
st.write("Results of the Tukey HSD test:")
st.dataframe(tukey_results_df, height=400)
csv = tukey_results_df.to_csv(index=False)
st.download_button(label="Download Tukey HSD results as CSV", data=csv, file_name='tukey_hsd_results.csv', mime='text/csv')
except Exception as e:
st.error(f"An error occurred during Tukey's HSD test: {str(e)}")
except ValueError as e:
st.error(f"An error occurred: {str(e)}.")
The “chi_square_test()” function checks whether there is a statistically significant relationship between two categorical variables. As only categorical variables can be used, the option to activate logarithmic scaling is not required. Specifically, whether the frequency of observations in the categories is independent of each other or whether there is a correlation. The user selects two of the existing categorical variables. The NaN values are removed and only the top 10 most frequent categories are selected for each variable in order to keep the analysis manageable “value_counts().nlargest(10).index”.
A crosstab “contingency_table” is created, which shows the frequencies of the combinations of categories in the two selected variables using a heatmap. If the crosstab is not valid (too little data or only one category), the test is not performed [8].

The test calculates various values. The chi-square value “chi2” determines the measure of the difference between the observed and expected frequencies. A strong difference is present with high values. As with the other analyses, the p-value “p” shows whether the difference is significant. The number of degrees of freedom of the test “dof” is indicated as well as the expected frequencies “expected”.
def chi_square_test(df, categorical_columns):
cat_var1 = st.selectbox("Choose the first group variable:", categorical_columns)
cat_var2 = st.selectbox("Choose the second group variable:", categorical_columns)
if st.button("Perform Chi-square test"):
df_clean = df[[cat_var1, cat_var2]].dropna()
top_cat_var1 = df_clean[cat_var1].value_counts().nlargest(10).index
top_cat_var2 = df_clean[cat_var2].value_counts().nlargest(10).index
df_filtered = df_clean[df_clean[cat_var1].isin(top_cat_var1) & df_clean[cat_var2].isin(top_cat_var2)]
try:
contingency_table = pd.crosstab(df_filtered[cat_var1], df_filtered[cat_var2])
if contingency_table.empty or contingency_table.shape[0] < 2 or contingency_table.shape[1] < 2:
st.error("The contingency table is invalid. Check the variables.")
else:
chi2, p, dof, expected = stats.chi2_contingency(contingency_table)
st.markdown(f"**Chi-square:** {chi2}")
st.markdown(f"**p-Value:** {p}")
st.write("**Heatmap of the contingency table:**")
fig, ax = plt.subplots(figsize=(12, 10)) # Larger display
sns.heatmap(contingency_table, annot=False, cmap="YlGnBu", ax=ax)
ax.set_title(f"Heatmap of the contingency table: {cat_var1} vs. {cat_var2} top 10")
plt.xticks(rotation=90)
st.pyplot(fig)
except ValueError as e:
st.error(f"An error occurred: {str(e)}.")
The selection of the available regression analyses (linear, logistic and multivariate) is similar to the selection of the various hypothesis tests. Once an analysis method has been selected, a brief explanation is displayed and the corresponding function is called up.
At the beginning of the “linear_regression()” function, a correlation matrix is created from all available numerical variables in the uploaded dataset “corr_matrix = df[numerical_columns].corr()”. The matrix is intended to help the user understand the relationships between the variables in order to identify the variables for which regression analyses are appropriate and those for which they are not (multicollinearity).
Finally, the dependent variable and one or more independent variables are selected. The data is cleaned and a linear regression model is created for all selected independent variables “model = LinearRegression()”. The regression coefficient and the intercept are specified. After the overall model has been run, a separate linear regression model is created for each independent variable and represented by a scatterplot [9].

The regression coefficient shown indicates the extent to which the dependent variable is changed when the respective independent variable is changed by one unit. Assuming that all other variables remain constant. The value that the dependent variable assumes when all independent variables are zero is indicated by the intercept.
def linear_regression(df, numerical_columns):
st.write("**Correlation matrix of numerical variables:**")
corr_matrix = df[numerical_columns].corr()
fig, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', ax=ax)
st.pyplot(fig)
dependent_var = st.selectbox("Choose the dependent variable:", numerical_columns)
independent_vars = st.multiselect("Choose the independent variables:", numerical_columns)
if independent_vars:
if st.button("Perform regression"):
X = df[independent_vars].dropna()
y = df[dependent_var].loc[X.index]
y = y.dropna()
X = X.loc[y.index]
if y.isnull().values.any():
st.error("The dependent variable still contains missing values. Please clean the data.")
else:
model = LinearRegression()
model.fit(X, y)
st.markdown("**Regression coefficients:**")
for var, coef in zip(independent_vars, model.coef_):
st.write(f"- {var}: {coef}")
st.write(f"**Intercept:** {model.intercept_}")
for var in independent_vars:
X_single_var = X[[var]] # Use only the current independent variable
model_single = LinearRegression()
model_single.fit(X_single_var, y)
fig, ax = plt.subplots()
ax.scatter(X[var], y, edgecolor='none', facecolors='blue', s=5, label='Data points')
ax.plot(X[var], model_single.predict(X_single_var), color='red', label='Regression line')
ax.set_xlabel(var)
ax.set_ylabel(dependent_var)
ax.set_title(f"{dependent_var} vs {var}")
ax.legend()
st.pyplot(fig)
As with the other functions, the user selects dependent and independent variables at the beginning. In this analysis method, the dependent variable must be binary (0/1). To demonstrate the function, I have created some data that has nothing to do with the dataset used so far. Alternatively, you can also manually adjust the values of variables, as long as there are not too many categories. If an incorrect variable is selected, a corresponding error message is displayed.
If everything is defined correctly, the logistic regression is performed and the model uses the independent variables to model the probability for the target variable. Specifically, this is the probability that an event will occur. The coefficients are specified for each independent variable and the logistic function is visualized. This shows how the probability of the target result (1 instead of 0) changes when the independent variable changes [10].

In the scatterplot, the red line represents the prediction probability for the target result, i.e. the probability that result 1 will occur. The independent variable varies. The “logistic_regression()” function is very well suited to binary classification problems where you want to predict the occurrence of an event based on several factors.
def logistic_regression(df, numerical_columns):
dependent_var = st.selectbox("Choose the dependent variable (binary):", numerical_columns)
independent_vars = st.multiselect("Choose the independent variables:", numerical_columns)
if independent_vars:
if st.button("Perform logistic regression"):
X = df[independent_vars].dropna()
y = df[dependent_var].loc[X.index].dropna()
X = X.loc[y.index]
unique_values = y.unique()
if len(unique_values) != 2:
st.error("The dependent variable must be binary (e.g., 0 and 1).")
else:
model = LogisticRegression()
model.fit(X, y)
st.write("**Logistic regression coefficients:**")
for var, coef in zip(independent_vars, model.coef_[0]):
st.write(f"- {var}: {coef}")
st.write(f"**Intercept:** {model.intercept_[0]}")
for var in independent_vars:
fig, ax = plt.subplots()
ax.scatter(X[var], y, label='Data points')
x_range = np.linspace(X[var].min(), X[var].max(), 300).reshape(-1, 1)
X_copy = pd.DataFrame(np.tile(X.mean().values, (300, 1)), columns=X.columns)
X_copy[var] = x_range.flatten() # Vary the current variable var
y_prob = model.predict_proba(X_copy)[:, 1]
ax.plot(x_range, y_prob, color='red', label='Logistic function')
ax.set_xlabel(var)
ax.set_ylabel(f'Probability ({dependent_var})')
ax.set_title(f'Logistic regression: {dependent_var} vs {var}')
ax.legend()
st.pyplot(fig)
In multivariate regression analysis, the user must select several dependent variables and one or more independent variables. The analysis examines how the dependent variables are influenced by the independent variables. After the variable selection, the NaN values are removed again and an error message is displayed if necessary. The model outputs the regression coefficient and the intercept for all dependent variables.
A scatterplot with regression line is created for all combinations of independent and dependent variables. This function makes it possible to analyze several target variables simultaneously and to model their relationship to several predictors [11].

def multivariate_regression(df, numerical_columns):
dependent_vars = st.multiselect("**Choose the dependent variables (multiple):**", numerical_columns)
independent_vars = st.multiselect("**Choose the independent variables:**", numerical_columns)
if dependent_vars and independent_vars:
if st.button("Perform multivariate regression"):
X = df[independent_vars].dropna()
Y = df[dependent_vars].loc[X.index].dropna()
X = X.loc[Y.index]
if X.shape[1] != len(independent_vars) or Y.shape[1] != len(dependent_vars):
st.error("The number of independent or dependent variables does not match.")
return
model = LinearRegression()
model.fit(X, Y)
st.write("**Multivariate regression coefficients:**")
for i, dep_var in enumerate(dependent_vars):
st.write(f"nFor the dependent variable: **{dep_var}**")
st.write(f"Intercept: {model.intercept_[i]}")
for var, coef in zip(independent_vars, model.coef_[i]):
st.write(f"- {var}: {coef}")
for dep_var in dependent_vars:
for var in independent_vars:
fig, ax = plt.subplots()
ax.scatter(X[var], Y[dep_var], label='Data points')
x_range = np.linspace(X[var].min(), X[var].max(), 300).reshape(-1, 1)
X_copy = pd.DataFrame(np.tile(X.mean().values, (300, 1)), columns=X.columns)
X_copy[var] = x_range.flatten()
y_pred = model.predict(X_copy)
ax.plot(x_range, y_pred[:, dependent_vars.index(dep_var)], color='red', label='Regression line')
ax.set_xlabel(var)
ax.set_ylabel(dep_var)
ax.set_title(f'Multivariate regression: {dep_var} vs {var}')
ax.legend()
st.plotly_chart(fig)
This analysis method performs an analysis over time. For this purpose, a given time series is grouped by year and the annual average of a value is calculated and displayed. A time variable is required for the analysis; if the dataset used does not contain one, it cannot be performed. In the dataset I have selected, there is the variable “release_date”, which contains the release date of the respective game.
The selected time variable is converted to the date format “df[time_var]”. If the data points are invalid, they are converted to NaN values and removed “df = df.dropna(subset=[time_var])”. The data is then grouped by year “df[‘year’] = df[time_var].dt.year” and the annual average for the specified value variable “value_var” is calculated “yearly_avg”. The minimum and maximum annual average values of the value variable are calculated as well as the overall average across all data points “overall_avg”. The annual average of the value variable per year is then displayed via a line chart. The overall average is integrated on the horizontal line. The values are displayed alternately above and below the data points to improve readability [12].

Important statistical key figures are displayed below the diagram, which can be easily interpreted as in the descriptive analysis using an LLM. Specifically, the standard deviation, the variance and the minimum and maximum of the value variable as well as the year are displayed. The “perform_time_series_analysis()” function is suitable for analyzing time trends in a data series. This allows an initial analysis of the variability over time.
def perform_time_series_analysis(df, time_var, value_var):
df[time_var] = pd.to_datetime(df[time_var], errors='coerce')
df = df.dropna(subset=[time_var])
if df.empty:
st.error("**Error:** The time variable has an incorrect format.")
else:
df['year'] = df[time_var].dt.year
yearly_avg = df.groupby('year')[value_var].mean().reset_index()
y_min = yearly_avg[value_var].min()
y_max = yearly_avg[value_var].max()
y_range = y_max - y_min
y_buffer = y_range * 0.05
overall_avg = df[value_var].mean()
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(yearly_avg['year'], yearly_avg[value_var], marker='o', label='Yearly average')
ax.axhline(overall_avg, color='red', linestyle='--', label=f'Overall average: {overall_avg:.2f}')
ax.set_title(f'Average {value_var} per year')
ax.set_xlabel('Year')
ax.set_ylabel(f'Average {value_var}')
ax.set_ylim(y_min - y_buffer, y_max + y_buffer)
ax.text(yearly_avg['year'].max() - (yearly_avg['year'].max() - yearly_avg['year'].min()) * 0.05,
overall_avg + y_buffer,
f'{overall_avg:.2f}', color='red', ha='right', va='center')
for i in range(len(yearly_avg)):
if i % 2 == 0:
ax.text(yearly_avg['year'][i], yearly_avg[value_var][i] + y_buffer/2,
f'{yearly_avg[value_var][i]:.2f}', color='blue', ha='center', va='bottom')
else:
ax.text(yearly_avg['year'][i], yearly_avg[value_var][i] - y_buffer/2,
f'{yearly_avg[value_var][i]:.2f}', color='blue', ha='center', va='top')
plt.xticks(rotation=45)
ax.legend()
st.pyplot(fig)
st.write(f"**Standard deviation:** {df[value_var].std():.2f}")
st.write(f"**Variance:** {df[value_var].var():.2f}")
st.write(f"**Minimum {value_var}:** {y_min:.2f} in year {yearly_avg.loc[yearly_avg[value_var].idxmin(), 'year']}")
st.write(f"**Maximum {value_var}:** {y_max:.2f} in year {yearly_avg.loc[yearly_avg[value_var].idxmax(), 'year']}")
As with the hypothesis tests and regression analyses, there are also various options to choose from in the area of clustering methods. The selection function has a similar structure to the others. A method is selected and the corresponding function is executed. A brief explanation of the method is also shown here. Depending on the method, the number of clusters must be defined. For k-Means and hierarchical clustering, a maximum of 10 clusters can be defined. For DBSCAN, the radius “eps” and the minimum number of points per cluster “min_samples” are queried. At least two numerical variables must be selected for each method.
The k-Means algorithm divides the data into “n_clusters”. The points are grouped in such a way that the distance between the points within the cluster is minimized. The number of clusters is determined by the user. Depending on the number, the algorithm calculates which data points belong to which cluster. The result is sent to the “visualize_clusters()” function for visualization [13].
def perform_kmeans(X, n_clusters):
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
X['Cluster'] = kmeans.fit_predict(X)
visualize_clusters(X, 'k-Means Clustering')

A hierarchy of clusters is created here, whereby agglomerative or divisive methods can be used. Agglomerative clustering is used in the function, whereby each data point is initially considered as a separate cluster before they are successively merged. The number of clusters is determined by the user and the algorithm divides the data according to the number. The same function as for k-Means is used for visualization “visualize_clusters(X, ‘Hierarchical Clustering’)” [14].
def perform_hierarchical_clustering(X, n_clusters):
hierarchical_clustering = AgglomerativeClustering(n_clusters=n_clusters)
X['Cluster'] = hierarchical_clustering.fit_predict(X)
visualize_clusters(X, 'Hierarchical Clustering')

With this method, data points are grouped based on the density of their surroundings. The method is well suited to detecting outliers (noise) and finding clusters of any shape. Here, the user does not specify the number of clusters, but the maximum distance “eps” between two points before they are considered neighbors. The minimum number of points that occur in a cluster “min_samples” is also defined. The visualization is also created by “visualize_clusters()” [15].
def perform_dbscan(X, eps, min_samples):
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
X['Cluster'] = dbscan.fit_predict(X)
visualize_clusters(X, 'DBSCAN Clustering')

The results of the three different clustering methods are visualized in the “visualize_clusters” function using Principal Component Analysis (PCA). The dimensions of the data are reduced by PCA to two components “n_components” in order to be able to display the clusters. It is checked whether there are enough data points and variables “num_samples”; if this is not the case, an error message is displayed. The clusters are visualized by a scatterplot that shows the data points in the first two PCA components.
The clusters are displayed in different colors “cmap=‘tab10’”. In the diagrams, the axis label “ax.set_x/ylabel” and the legend “legend_labels” are adapted for better interpretation. The size of the data points “s” and the transparency “alpha” have also been adjusted to improve visibility. Outliers are automatically assigned to cluster -1 in DBSCAN. A table with the average values of the variable for each cluster is displayed below the visualization “st.dataframe(cluster_means)”.
def visualize_clusters(X, title):
num_samples, num_features = X.shape
n_components = min(num_samples, num_features, 2)
if n_components < 2:
st.error("Not enough data points or variables to perform PCA.")
return
pca = PCA(n_components=n_components)
try:
X_pca = pca.fit_transform(X.drop(columns=['Cluster']))
fig, ax = plt.subplots(figsize=(10, 6))
scatter = ax.scatter(X_pca[:, 0], X_pca[:, 1], c=X['Cluster'], cmap='tab10', s=25, alpha=0.4)
ax.set_title(title)
ax.set_xlabel(f'PCA 1' if n_components >= 1 else '')
ax.set_ylabel(f'PCA 2' if n_components == 2 else '')
cluster_counts = X['Cluster'].value_counts()
legend_labels = [f"Cluster {int(cluster)} ({count} points)" for cluster, count in cluster_counts.items()]
legend1 = ax.legend(handles=scatter.legend_elements()[0], labels=legend_labels)
ax.add_artist(legend1)
st.pyplot(fig)
st.write(f"**Average values per cluster:**")
cluster_means = X.groupby('Cluster').mean()
st.dataframe(cluster_means)
except ValueError as e:
st.error(f"**Error:** Not enough variables were selected.")
In this first version of the app, the output of the statistical calculations is only analyzed in the descriptive area. The key figures are interpreted using the “query_llm_via_cli” function. Specifically, the function is used to communicate with the LLM via a command line (CLI). To achieve this, the Python module “subprocess” is used to start the process via the command line. The LLM is started via the command [“ollama”, “run”, “llama3.1”]. The input is stored in “stdin”, the output in “stout”.
Errors and warnings are stored in “stderr”, which hopefully do not occur. The input is sent to the model via “process.communicate”. Specifically, the created “context” is sent to the function to communicate with the LLM. If there is no response from the model, a timeout mechanism “timeout=40” is included, which stops the execution after 40 seconds. Depending on the computing power of the system used, a response from the model should be displayed much earlier. The model’s response is cleaned up and passed to “extract_relevant_answer” in order to extract relevant information [1].
def query_llm_via_cli(input_text):
"""Sends the question and context to the LLM and receives a response"""
try:
process = subprocess.Popen(
["ollama", "run", "llama3.1"],
stdin=subprocess.PIPE,
stdout=subprocess.PIPE,
stderr=subprocess.PIPE,
text=True,
encoding='utf-8',
errors='ignore',
bufsize=1
)
stdout, stderr = process.communicate(input=f"{input_text}n", timeout=40)
if process.returncode != 0:
return f"Error in the model request: {stderr.strip()}"
response = re.sub(r'x1b[.*?m', '', stdout)
return extract_relevant_answer(response)
except subprocess.TimeoutExpired:
process.kill()
return "Timeout for the model request"
except Exception as e:
return f"An unexpected error has occurred: {str(e)}"
def extract_relevant_answer(full_response):
response_lines = full_response.splitlines()
if response_lines:
return "n".join(response_lines).strip()
return "No answer received"
The structure of the app is defined by the “main()” function. The title is set “st.title()” and the sidebar for uploading the dataset in CSV or Excel format “uploaded_file” is submitted. Once a file has been uploaded, it is analyzed and the numerical and categorical variables are extracted. Here and in many other situations, “session_state” is used by Streamlit to store certain parameters that are relevant for the selection in the analysis methods.
The variables “numerical_columns” and “categorical_columns” are updated as soon as a new dataset is uploaded. Once data is available, the user can select from the various analysis methods. Once a method has been selected, it is displayed and can be carried out after the corresponding variables have been defined. The main function controls the interactive statistical analysis of the app.
As already mentioned, the app can be expanded to include other analysis methods due to the modular structure of the code. The functionality of interpreting statistical key figures using an LLM can also be transferred to other methods. Llama3.1 (8B) from Meta is currently used, but another LLM (e.g. Mistral) from Ollama can also be used. The command in the “query_llm_via_cli” function must then be adapted accordingly.
Depending on the available power, models with more parameters can also be used. The design of the diagrams can be further refined, as can the transmitted contexts, in order to improve the output of the LLM. Alternatively, you can also create a new model file to adjust certain parameters (e.g. parameters) of the LLM and thereby improve the interpretation of the data.
The app code can be downloaded from the following GitHub repository. The app is started in the corresponding directory using the following command:
Streamlit run app.py
In this article, I showed how Streamlit can be used to create an app that can be used to analyze datasets using various methods. I also showed how an interpretation can be integrated into the app using an LLM, which results in real added value. Data is not only automatically visualized and statistical parameters are output, but also classified. The application offers a lot of potential for further development. I have listed some suggestions in the penultimate section. Have fun using and customizing the app.
[1] Pietrusky, S. (2024, August 21). How to talk to a PDF file without using proprietary models: CLI, Streamlit, Ollama. Towards Data Science. URL
[2] Maven Analytics. (2024, Juni 10.). Data Playground, Video Game Sales. URL
[3] Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: Data mining, inference, and prediction (2nd ed.). Stanford University. URL
[4] Bruce, P., Bruce, A., & Gedeck, P. (2021). Praktische Statistik für Data Scientists: 50+ essenzielle Konzepte mit R und Python (2nd ed.). O’Reilly.
[5] VanderPlas J. (2017). Python Data Science Handbook: Essential Tools for Working with Data. O’Reilly. URL
[6] Fahrmeir, L., Künstler, R., Pigeot, I., & Tutz, G. (2016). Statistik: Der Weg zur Datenanalyse (8th ed.). Springer.
[7] Montgomery, D. C. (2012). Design and analysis of experiments (8th ed.). Wiley. URL
[8] Moore, D. S., McCabe, G. P., Craig, B. A., & Duckworth, W. M. (2021). Introduction to the practice of statistics (10th ed.). W. H. Freeman.
[9] Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to linear regression analysis (5th ed.). Wiley. URL
[10] Hosmer, D. W., Lemeshow, S., & Sturdivant, R. X. (2013). Applied logistic regression (3rd ed.). Wiley.
[11] Johnson, R. A., & Wichern, D. W. (2007). Applied multivariate statistical analysis (6th ed.). Pearson. URL
[12] Box, G. E. P., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis: Forecasting and control (5th ed.). Wiley. URL
[13] Witten, I. H., & Frank, E. (2005). Data mining: Practical machine learning tools and techniques (2nd ed.). Morgan Kaufmann.URL
[14] Everitt, B. S., Landau, S., Leese, M., & Stahl, D. (2011). Cluster analysis (5th ed.). Wiley. URL
[15] Aggarwal, C. C., & Reddy, C. K. (2014). Data Clustering: Algorithms and Applications. CRC Press URL

ASCVIT V1: Automatic Statistical Calculation, Visualization and Interpretation Tool was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
ASCVIT V1: Automatic Statistical Calculation, Visualization and Interpretation Tool