
Originally appeared here:
AWS recognized as a first-time Leader in the 2024 Gartner Magic Quadrant for Data Science and Machine Learning Platforms

Originally appeared here:
AWS recognized as a first-time Leader in the 2024 Gartner Magic Quadrant for Data Science and Machine Learning Platforms



TL;DR

Tango de Mundial is the annual Argentine Tango competition held in Buenos Aires, Argentina. Dancers from around the world travel to Buenos Aires to compete for the title of World Champion.
In 2024 around 500 dance couples (1000 dancers) competed in the preliminary round. A very small portion of dancers made it to the semi-final round and only about 40 couples make it the final round. Simply making it the final round in 2024 puts you above the 95th percentile of world wide competitors.
Many finalist use this platform to advance their professional careers while the title of World Champion cements your face in tango history and all but guarantees that you’ll work as a professional dancer for as long as you desire. Therefore, for a lot of dancers, their fate lies in what the judges think of their dancing.
In this article we will perform several statistical analyses on the scoring bias of two judging panels each comprising of 10 judges. Each judge has their own answer to the question “What is tango?” Each judge has their own opinion of what counts for quality for various judging criteria: technique, musicality, embrace, dance vocabulary, stage presence (i.e. do you look the part), and more. As you can already tell these evaluations are highly subjective and will unsurprisingly result in a lot of bias between judges.
Note: Unless explicitly stated otherwise, all data visualizations (i.e. plots, charts, screen shots of data frames) are the original work of the author.
You can find all code used for this analysis in my GitHub Portfolio.
my_portfolio/Argentine_Tango_Mundial at main · Alexander-Barriga/my_portfolio
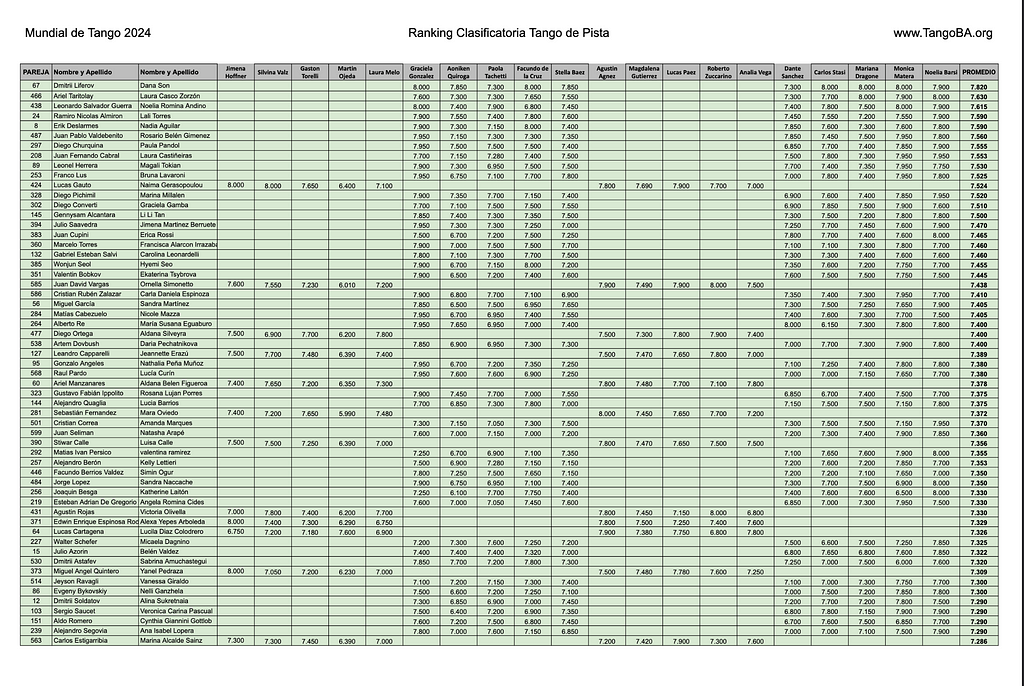
Before we dive into the analysis let’s address some limitation we have with the data. You can directly access the preliminary round competition scores in this PDF file.
Ranking-Clasificatoria-Tango-de-Pista-Mundial-de-tango-2024.pdf
Despite these issues with the data, the data from Tango Munidal is the largest and most representative dataset of world wide argentine tango dancers that we have available.
In addition to being a data scientist, I am a competitive argentine tango dancer. While I didn’t compete in the 2024 Munidal de Tango, I have been diligently training in this dance for many years (in addition to other dances and martial arts). I am a dancer, a martial artist, a performer, and caretaker of tango.
While my opinion represents only a single, subjective voice on argentine tango, it is a genuine and informed one.
We will know perform several statistical test to asses if and where scoring bias is present. The outline of the analysis is as follows:
Take another look at the top performing dance couples from page 1 of the score data table again:

Reading the column names from left to right that represent the judge’s names between Jimena Hoffner and Noelia Barsel you’ll see that:
Notice anything? Notice how dancers that were judged by panel 2 show up in much larger proportion and dancers that were judge by panel 1. If you scroll through the PDF of this data table you’ll see that this proportional difference holds up throughout the competitors that scored well enough to advance to the semi-final round.
Note: The dancers shaded in GREEN advanced to the semi-final round. While dancers NOT shaded in Green didn’t advance to the semi-final round.
So this begs the question, is this proportional difference real or is it due to random sampling, random assignment of dancers to one panel over the other? Well, there’s a statistical test we can use to answer this question.
We are going to use the two-tailed z-test to test if there is a significant difference between the two proportions in either direction. We are interested in whether one proportion is significantly different from the other, regardless of whether it is larger or smaller.
Our dataset mets all these assumptions.
Null Hypothesis: The proportions from each distribution are the same.
Alt. Hypothesis: The proportions from each distribution are the NOT the same.
2. Pick a Statistical Significance level
The default value for alpha is 0.05 (5%). We don’t have a reason to relax this value (i.e. 10%) or to make it more stringent (i.e. 1%). So we’ll use the default value. Alpha represents our tolerance for falsely rejecting the Null Hyp. in favor of the Alt. Hyp due to random sampling (i.e. Type 1 Error).
Next, we carry out the test using the Python code provided below.
def plot_two_tailed_test(z_value):
# Generate a range of x values
x = np.linspace(-4, 4, 1000)
# Get the standard normal distribution values for these x values
y = stats.norm.pdf(x)
# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x, y, label='Standard Normal Distribution', color='black')
# Shade the areas in both tails with red
plt.fill_between(x, y, where=(x >= z_value), color='red', alpha=0.5, label='Right Tail Area')
plt.fill_between(x, y, where=(x <= -z_value), color='red', alpha=0.5, label='Left Tail Area')
# Define critical values for alpha = 0.05
alpha = 0.05
critical_value = stats.norm.ppf(1 - alpha / 2)
# Add vertical dashed blue lines for critical values
plt.axvline(critical_value, color='blue', linestyle='dashed', linewidth=1, label=f'Critical Value: {critical_value:.2f}')
plt.axvline(-critical_value, color='blue', linestyle='dashed', linewidth=1, label=f'Critical Value: {-critical_value:.2f}')
# Mark the z-value
plt.axvline(z_value, color='red', linestyle='dashed', linewidth=1, label=f'Z-Value: {z_value:.2f}')
# Add labels and title
plt.title('Two-Tailed Z-Test Visualization')
plt.xlabel('Z-Score')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
# Show plot
plt.savefig(f'../images/p-value_location_in_z_dist_z_test_proportionality.png')
plt.show()
def two_proportion_z_test(successes1, total1, successes2, total2):
"""
Perform a two-proportion z-test to check if two population proportions are significantly different.
Parameters:
- successes1: Number of successes in the first sample
- total1: Total number of observations in the first sample
- successes2: Number of successes in the second sample
- total2: Total number of observations in the second sample
Returns:
- z_value: The z-statistic
- p_value: The p-value of the test
"""
# Calculate sample proportions
p1 = successes1 / total1
p2 = successes2 / total2
# Combined proportion
p_combined = (successes1 + successes2) / (total1 + total2)
# Standard error
se = np.sqrt(p_combined * (1 - p_combined) * (1/total1 + 1/total2))
# Z-value
z_value = (p1 - p2) / se
# P-value for two-tailed test
p_value = 2 * (1 - stats.norm.cdf(np.abs(z_value)))
return z_value, p_value
min_score_for_semi_finals = 7.040
is_semi_finalist = df.PROMEDIO >= min_score_for_semi_finals
# Number of couples scored by panel 1 advancing to semi-finals
successes_1 = df[is_semi_finalist][panel_1].dropna(axis=0).shape[0]
# Number of couples scored by panel 2 advancing to semi-finals
successes_2 = df[is_semi_finalist][panel_2].dropna(axis=0).shape[0]
# Total number of couples that where scored by panel 1
n1 = df[panel_1].dropna(axis=0).shape[0]
# Total sample of couples that where scored by panel 2
n2 = df[panel_2].dropna(axis=0).shape[0]
# Perform the test
z_value, p_value = two_proportion_z_test(successes_1, n1, successes_2, n2)
# Print the results
print(f"Z-Value: {z_value:.4f}")
print(f"P-Value: {p_value:.4f}")
# Check significance at alpha = 0.05
alpha = 0.05
if p_value < alpha:
print("The difference between the two proportions is statistically significant.")
else:
print("The difference between the two proportions is not statistically significant.")
# Generate the plot
# P-Value: 0.0000
plot_two_tailed_test(z_value)
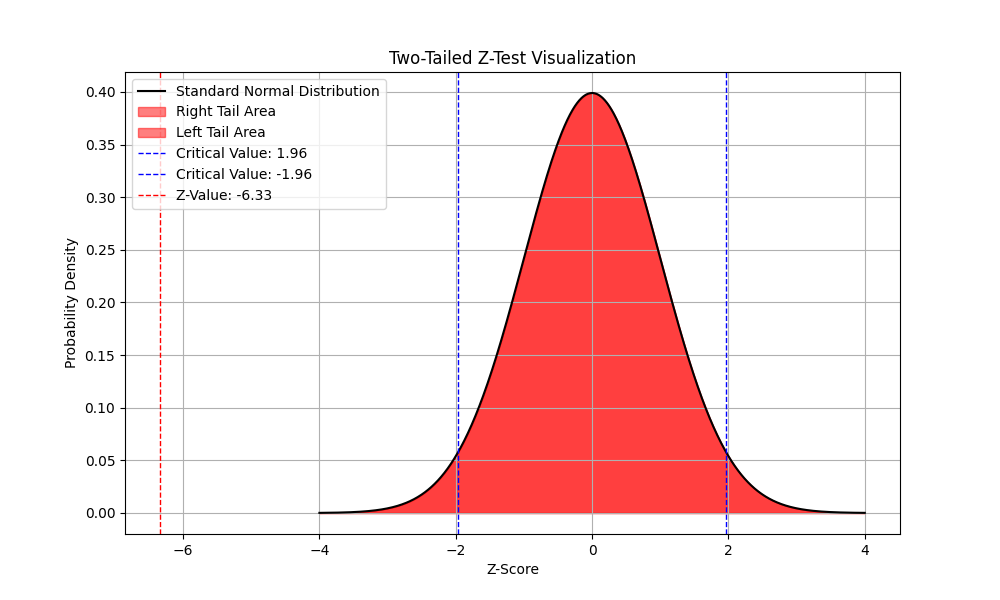
The plot shows that the Z-value calculated exists far outside the range of z-values that we’d expect to see if the null hypothesis is true. Thus resulting in a p-value of 0.0 indicating that we must reject the null hypothesis in favor of the alternative.
This means that the differences in proportions is real and not due to random sampling.
Our first statistical test for bias has provided evidence that there is a positive bias in scores for dancers judged by panel 2, representing a nearly 2x boost.
Next we dive into the scoring distributions of each individual judge and see how their individual biases affect their panel’s overall bias.
In this section we will analyze the individual score distributions and biases of each judge. The following 20 histograms represent the scores that each judge gave a dancer. Remember that each dancer was scored by all 10 judges in panel 1 or panel 2. The judge’s histograms are laid out randomly, i.e. column one doesn’t represent judges from panel 1.
Note: Judges score on a scale between 1 and 10.
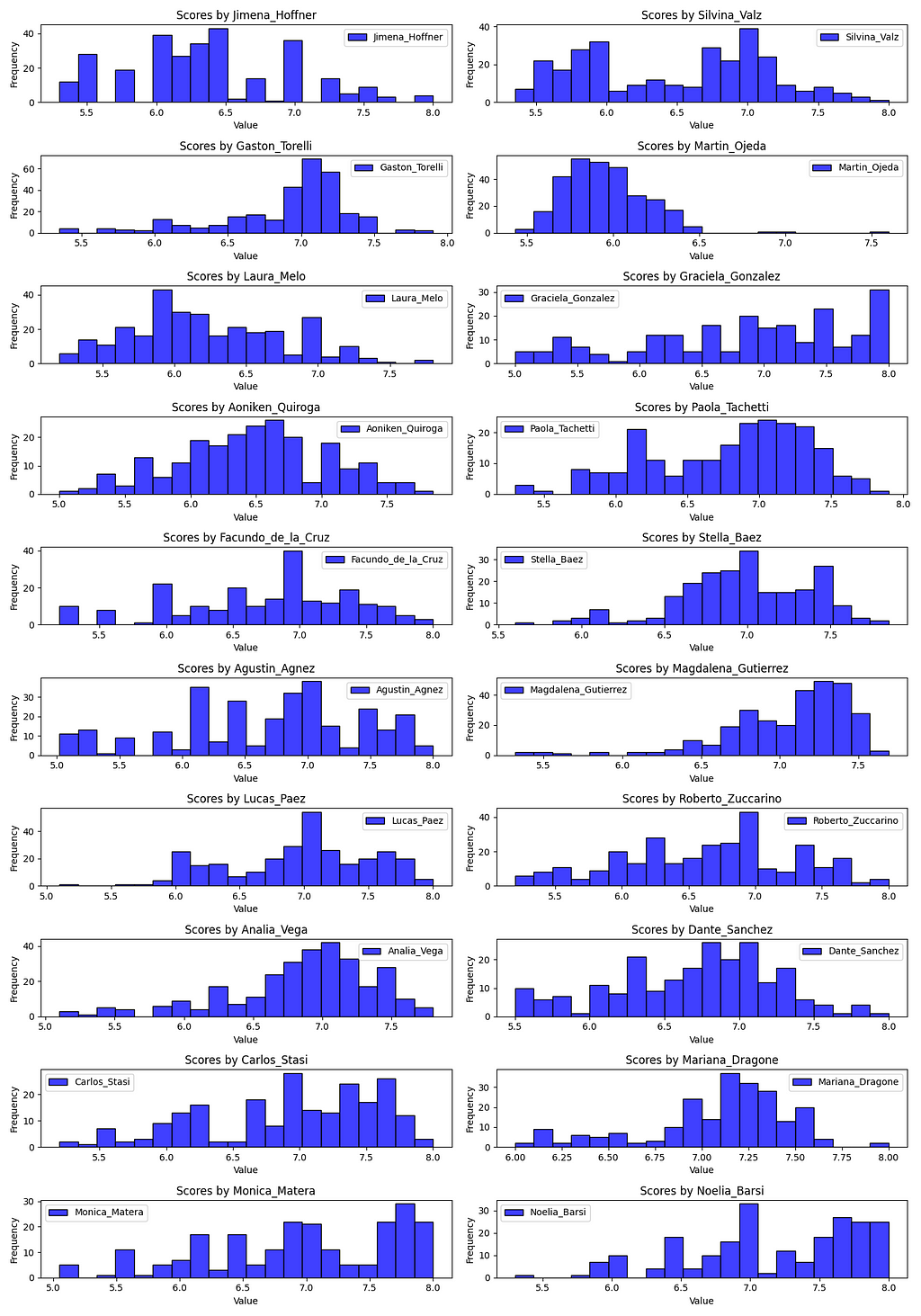
Notice how some judges score much more harshly than other judges. This begs the questions:
We will answer question 1 in section 3.
We will answer question 2 in section 4.
As we saw in the histograms above, judge Martin Ojeda is the harshest dance judge. Let’s look at his QQ-Plot.
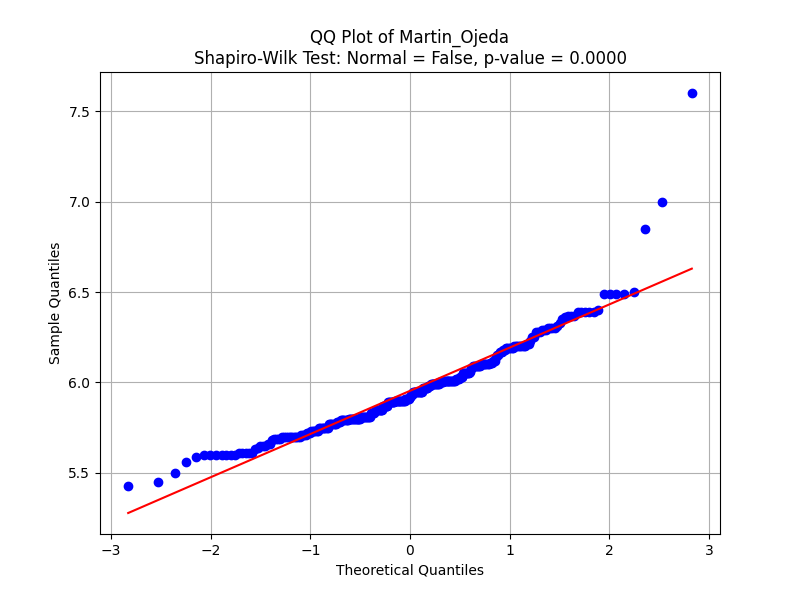
Lower-left deviation (under -2 on the x-axis): In the lower quantile region (far-left), the data points actually deviate above the red line. This indicates higher-than-expected scores for the weakest performances. Martin could be sympathetically scoring dance couples slightly higher than he feels they deserve. A potential reason could be that Martín wishes to avoid hurting the lowest-performing competitors with extremely poor scores, thus giving slightly higher ones.
Dilution of Score Differences: If weaker performances are overrated, it can compress the scoring range between weaker and mid-tier competitors. This might make the differences between strong, moderate, and weak performances less clear.
Balance between low and high scores: Although Martín overrates weaker performers, notice that in the mid-range (6.0–7.0), the scores closely follow a normal pattern, showing more neutral behavior. However, this is counterbalanced by his generous scoring at the top end (positive bias for top performers), suggesting that Martín tends to “pull up” both ends of the performance spectrum.
In this next section, we will identify Martin’s outlier score for what he considers the best performing dance couple assgined to his panel. We will give the dance couple’s score more context when comparing it with scores from other judges on the panel.
There are 19 other QQ-Plots in the Jupyter Notebook which we will not be going over in this article as it would be make this article unbearably long. However feel free to take a look yourself.
In this section we will answer the first question that was asked in the previous section. This section will analyze the bias in scoring of individual judges. The next section will look at the bias in scoring between panels.
What is the distribution of bias between the judges? In other words, which judges score harsher and which score more lenient?
We are going to perform iterative T-test to check if a judge’s mean score is statistically different from the mean of the mean scores all of their 19 peers; i.e. take the mean of the other 19 judges’ mean scores.
# Calculate mean and standard deviation of the distribution of mean scores
distribution_mean = np.mean(judge_means)
distribution_std = np.std(judge_means, ddof=1)
# Function to perform T-test
def t_test(score, mean, std_dev, n):
"""Perform a T-test to check if a score is significantly different from the mean."""
t_value = (score - mean) / (std_dev / np.sqrt(n))
# Degrees of freedom for the T-test
df = n - 1
# Two-tailed test
p_value = 2 * (1 - stats.t.cdf(np.abs(t_value), df))
return t_value, p_value
# Number of samples in the distribution
n = len(judge_means)
# Dictionary to store the test results
results = {}
# Iterate through each judge's mean score and perform T-test
for judge, score in zip(judge_features, judge_means):
t_value, p_value = t_test(score, distribution_mean, distribution_std, n)
# Store results in the dictionary
results[judge] = {
'mean_score': score,
'T-Value': t_value,
'P-Value': p_value,
'Significant': p_value < 0.05
}
# Convert results to DataFrame and process
df_judge_means_test = pd.DataFrame(results).T
df_judge_means_test.mean_score = df_judge_means_test.mean_score.astype(float)
df_judge_means_test.sort_values('mean_score')
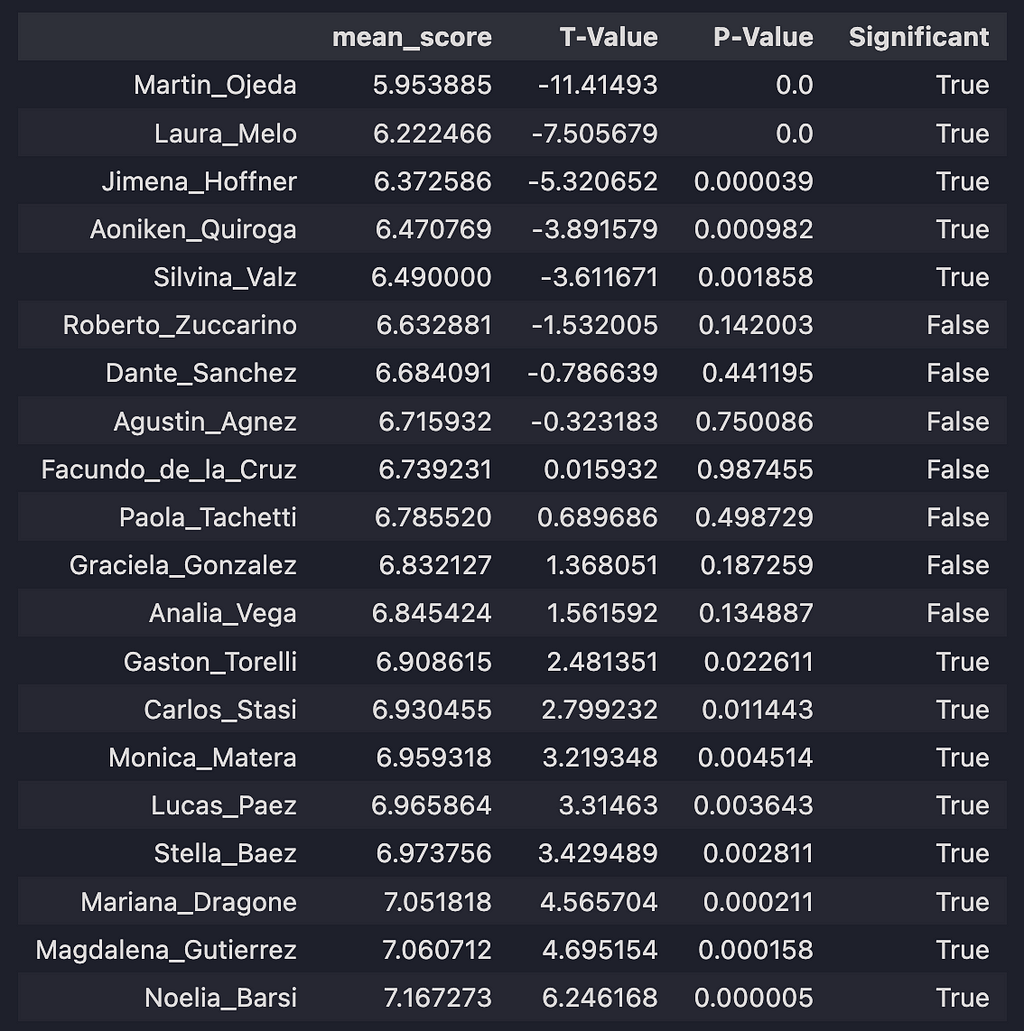
Here we have all 20 judges: their mean scores, their t statistics, p-values, and if the different between the individual judge’s mean score and the mean of the distribution of the other 19 judge’s means is statistically significant.
We have 3 groups of judges: those that score very harshly (statistically below average), those that typically give average scores (statistically within average), and those that score favorably (statistically above average).
Let’s focus on 3 representative judges: Martin Ojeda, Facundo do la Cruz, and Noelia Barsi.
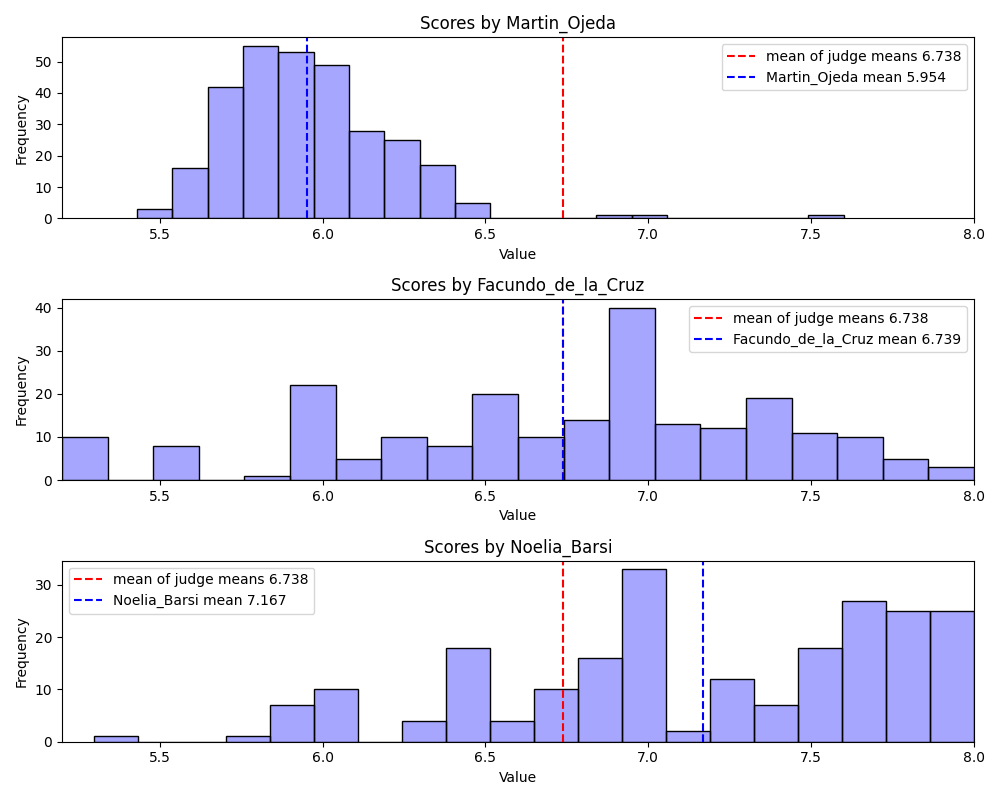
Notice that Martin Ojeda’s score distribution and mean (blue line) is shifted towards lower values as compared to the mean of the mean scores of all judges (red line). But we also see that his distribution is approximately normally distributed with the exception of a few outliers. We will return to the couple that scored 7.5 shortly. Almost any dance couple that gets judged by Martin will see their overall average score take a hit.
Facundo de la Cruz has an approximately normal distribution with a large variance. He represents the least biased judge relative to his peers. Almost any dance couple that gets judged by Facundo can expect a score that is typical of all the judges, so they don’t have to worry about negative bias but they are also unlikely to receive a high score boosting their overall average.
Noelia Baris represents the judge that tends to give more dancers a favorable score as compared to her peers. All dance couples should hope that Noelia gets assigned to their judge panel.
Now let’s return to Martin’s outlier couple. In Martin’s mind, Lucas Cartagena & Lucila Diaz Colodrero dance like outliers.
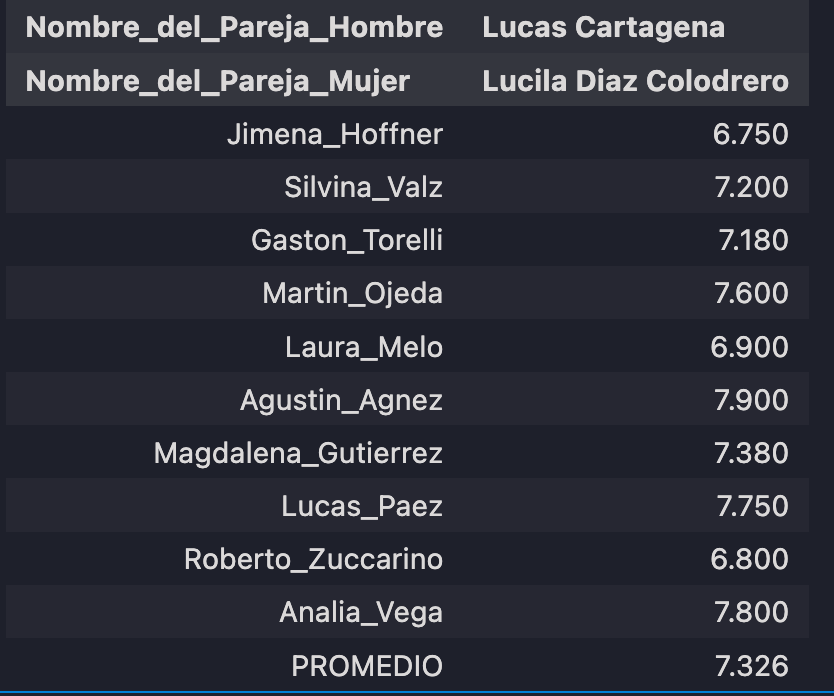
Here they are performing to a sub-category of tango music called Milonga, which is usually danced very differently than the other music categories, Tango and Waltz, and typically doesn’t include any spinning and instead includes small, quick steps that greatly emphasize musicality. I can tell you that they do perform well in this video and I think most dancers would agree with that assessment.
Enjoy the performance.
In this section we test for bias between Panel 1 and Panel 2 by answering the following questions:
Do the scoring biases of judges get canceled out by their peers on the their panel? If not, is there a statistical difference between their means?
We will test for panel bias in two ways
Here we will rank and standardize the judge mean scores and calculate a bias for each panel. This is one way in which we can measure any potential biases that exist between judge panels.
panel_1 = judge_features[:5] + judge_features[10:15]
panel_2 = judge_features[5:10] + judge_features[15:]
df_judge_means = df_judge_means_test.sort_values('mean_score').mean_score
# Calculate ranks
ranks = df_judge_means.rank()
# Calculate mean and std of ranks
means_ranks = ranks.mean()
stds_ranks = ranks.std()
# Standardize ranks
df_judge_ranks = (ranks - means_ranks) / stds_ranks
df_judge_ranks
# these are the same judges sorted in the same way as before based on their mean scores
# except here we have converted mean values into rankings and standardized the rankings
# Now we want to see how these 20 judges are distributed between the two panels
# do the biases for each judge get canceled out by their peers on the same panel?
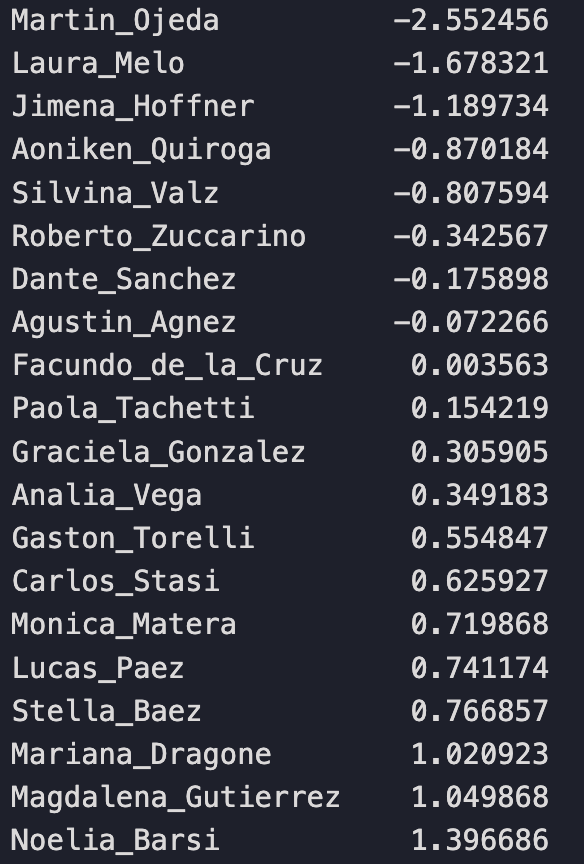
We’ll simply replace each judge’s mean score value with a ranking relative to their position to their peers. Martin is still the harshest, most negatively biased judge. Noelia is still the most positively biased judge.
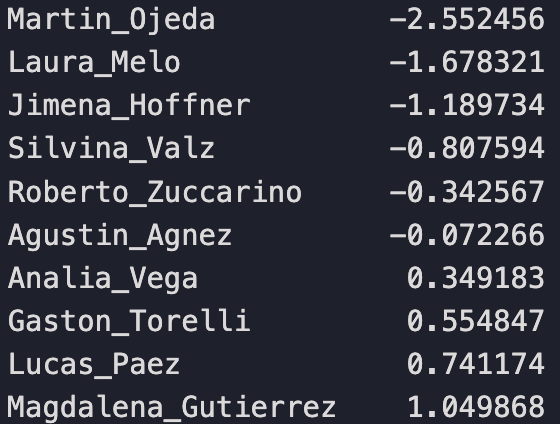
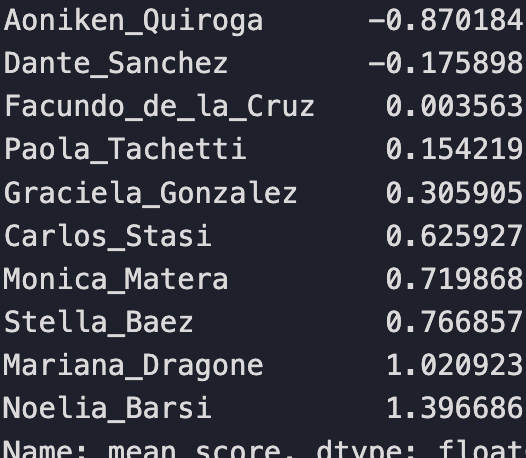
Notice that most judges in Panel 1 are negatively biased and only 4 are positive. While most judges on Panel 2 are positively biased with only 2 judges negatively biased and Facundo being approximately neutral.
Now if the intra-panel biases cancel out than the individual judge biases effectively don’t matter; any dance couple would be scored statistically fairly. But if the intra-panel biases don’t cancel, then there might be an unfair advantage present.
Panel 1 mean ranking value: -0.39478
Panel 2 mean ranking value: 0.39478
We find that the mean panel rankings reveal that the intra-panel biases do not cancel out, providing evidence that there is an advantage for a dance couple to be scored by Panel 2.
Next we following up on the previous results with an additional test for panel bias. The plot below shows two distributions. In blue we have the distribution of mean scores given by judges assigned to Panel 1. In orange we have the distribution of mean scores given by judges assigned to Panel 2.
In the plot you’ll see the mean of the mean scores for each panel. Panel 1 has a mean panel score of 6.62 and Panel 2 has a mean panel score of 6.86.
While a panel mean difference of 0.24 might seem small, know that the difference between advancing to the semi-final round is determined by a difference of 0.013
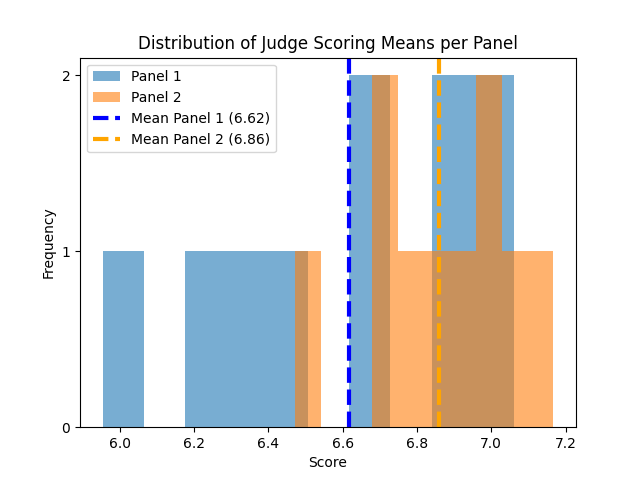
After performing a two sample T-test we find that the difference between the panel means is NOT statistically different. This test fails to provide additional evidence that there is a statistical difference in the bias between Panel 1 and Panel 2.
The P-value for this test is 0.0808 which isn’t too far off from 0.05, our default alpha value.
Law of Large Numbers
We know from The Law of Large Numbers that in small sample distributions (both panels have 10 data points) we commonly find a larger variance than the variance in its corresponding population distribution. However as the number of samples in the sample distributions increases, its parameters approach the value of the population distribution parameters (i.e mean and variance). This might be why the T-test fails to provide evidence that the panel biases are different, i.e. due to high variance.
Statistical Power
Another way to understand why we see the results that we see is due to Statistical Power. Statistical power refers to the probability that a test will correctly reject a false null hypothesis. Statistical power is influence by several factors
The most reliable way to increase our test’s statistical power is to collect more data points, however that is not possible here.
In this article we explore the preliminary round data from the 2024 Mundial de Tango Championship competition held in Buenos Aires. We analyze judge and panel scoring bias in 4 ways:
Evidence for Bias
No Evidence of Bias
My conclusion is that there is sufficient evidence of bias at the individual judge and at the panel level. Dancers that got assigned to Panel 2 did have a competitive edge. As such there is advice to give prospective competitive dancers looking for an extra edge in winning their competitions.
There are both non-machiavellian and machiavellian ways to increase your chances of winning. The results of this article inform (and background knowledge gained from experience) add credence to the machiavellian approaches.
Non-machiavellian
Machiavellian
I personally believe that, while useful, playing power games in dance competitions is silly. There is no substitute for raw, undeniable talent. This analysis is, ultimately, a fun passion project and opportunity to apply some statistical concepts on a topic that I greatly cherish.
Alexander Barriga is a data scientist and competitive Argentine Tango dancer. He currently lives in Los Angeles, California. If you’ve made it this far, please consider leaving feedback, sharing his article, or even reaching out to him directly with a job opportunity — he is actively looking for his next data science role!

Statistical Analysis on Scoring Bias was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Statistical Analysis on Scoring Bias
Go Here to Read this Fast! Statistical Analysis on Scoring Bias


A Deep Dive into Amazon’s Complementary Product Recommendation Framework
Originally appeared here:
P-Companion: Amazon’s Principled Framework for Diversified Complementary Product Recommendation



We have observed the existence of both unused and under-trained tokens in exploration of transformer based large language models (LLMs) such as ChatGPT, of which the tokenization and the model training stay as two separate processes. Unused tokens and under-trained tokens have the following different behaviors:
Ideally, the two types of tokens would have very low probabilities to be generated, or equivalently, have extremely negative logit values, so that they should not be generated by the LLMs. However, in practice, users have still found some unused tokens with important logits and the model can sometimes unfortunately predict them. This can lead to undesirable behaviors in LLMs.
Let us consider an LLM which unexpectedly generates nonsensical or inappropriate text because of some tokens that was never trained during the model training. Such occurrences can sometimes cause serious consequences, such as hallucination, leading to lack of accuracy and appropriateness.
We claim this issue is due to the separation between tokenization and the training process of LLMs. In general, these two aspects are never trained together and it did happen that a token in the model’s vocabulary fails to be trained and appears randomly in the output of the model.
In this article, we will demonstrate the existence of unused tokens, including under-trained ones, with some simple experiments using GPT-2 Small . We will also discuss techniques for identifying under-trained tokens.
In many LLMs, including GPT-2 Small on which our experiments are executed, there exist unused tokens, that is, tokens existing in the LLM’s vocabulary and were included during the process training but were not sufficiently seen.
In the following examples, we give two cases proving the existence of unused tokens:
In this experiment, we aim to show how GPT-2 Small struggles to reproduce unused tokens, even with very straightforward instructions. Let us now consider the following unused token:”ú” (u00fa). We would like to instruct GPT-2 small to repeat the token exactly as given by the input.
This is a very simple task: For the given input token “ú”, the model have to give the same token as output.
from transformers import GPT2LMHeadModel, GPT2Tokenizer
# Load pre-trained model (GPT-2 Small) and tokenizer
model_name = "gpt2" # GPT-2 Small (124M parameters)
model = GPT2LMHeadModel.from_pretrained(model_name)
tokenizer = GPT2Tokenizer.from_pretrained(model_name)
tokenizer.pad_token = tokenizer.eos_token
# Configure the model's `pad_token_id`
model.config.pad_token_id = model.config.eos_token_id
# Encode a prompt to generate text
token= "u00fa"
prompt_text = "Rpeats its input exactly" + ', '.join([f"Input: {token}, Output: {token}" for _ in range(20)])+ f"Input: {token}, Output: "
inputs = tokenizer(prompt_text, return_tensors="pt", padding=True)
# Generate text with attention mask
output = model.generate(
inputs['input_ids'],
attention_mask=inputs['attention_mask'], # Explicitly pass attention_mask
max_new_tokens=10, # Maximum length of the generated text
num_return_sequences=1, # Number of sequences to return
no_repeat_ngram_size=2, # Prevent repeating n-grams
do_sample=True, # Enable sampling
top_k=50, # Limit sampling to top k choices
top_p=0.95, # Use nucleus sampling
)
As you can see in the code above, we have designed a prompt as n-shot examples, instructing the model to give exactly the same specific token “ú” . What we see is that the model fails to predict this token: it gives some grabled text as “Output: – ß, *- *-, ” . In contrast, when we tested the same task with common tokens such as “a” , the model successfully predicted the correct output, showing the stark difference in performance between frequently encountered and unused tokens.
We now consider the range of unused tokens from indices 177 to 188, the range of unused tokens for GPT2 [1].
Our goal now is to generate sequences of repeated random tokens and evaluate the model’s performance on the repeated sequencee. As discussed in my previous blog post, “How to Interpret GPT-2 Small: Mechanistic Interpretability on Prediction of Repeated Tokens,” transformer-based LLMs have a strong ability to recognize and predict repeated patterns, even for small models such as GPT2 small.
For example, when the model encounters an ‘A’, it searches for the previous occurrence of ‘A’ or a token closely related to ‘A’ in the embedding space. It then identifies the subsequent token, ‘B’, and predicts that the next token following ‘A’ will be ‘B’ or a token similar to ‘B’ in the embedding space.
We begin by defining a function, generate_repeated_tokens which generated a sequence whose second half repeats the first half.
import torch as t
from typing import Tuple
# Assuming HookedTransformer and other necessary components are defined elsewhere.
t.manual_seed(42)
def generate_repeated_tokens(
model: HookedTransformer, seq_len: int, batch: int = 1
) -> Int[Tensor, "batch full_seq_len"]:
'''
Generates a sequence of repeated random tokens
Outputs are:
rep_tokens: [batch, 1+2*seq_len]
'''
bos_token = (t.ones(batch, 1) * model.tokenizer.bos_token_id).long() # generate bos token for each batch
rep_tokens_half = t.randint(177, 188, (batch, seq_len), dtype=t.int64)
rep_tokens = t.cat([bos_token, rep_tokens_half, rep_tokens_half], dim=-1).to(device)
return rep_tokens
Next, we define the run_and_cache_model_repeated_tokens function, which runs the model on the generated repeated tokens, returning the logits and caching the activations. We will use only logits here.
def run_and_cache_model_repeated_tokens(model: HookedTransformer, seq_len: int, batch: int = 1) -> Tuple[t.Tensor, t.Tensor, ActivationCache]:
'''
Generates a sequence of repeated random tokens, and runs the model on it, returning logits, tokens and cacheShould use the `generate_repeated_tokens` function above
Outputs are:
rep_tokens: [batch, 1+2*seq_len]
rep_logits: [batch, 1+2*seq_len, d_vocab]
rep_cache: The cache of the model run on rep_tokens
'''
rep_tokens = generate_repeated_tokens(model, seq_len, batch)
rep_logits, rep_cache = model.run_with_cache(rep_tokens)
return rep_tokens, rep_logits, rep_cache
Now we run the model using the defined run_and_cache_model_repeated_tokens function, generating both the tokens and the associated logits with the following code:
seq_len = 25
batch = 1
(rep_tokens, rep_logits, rep_cache) = run_and_cache_model_repeated_tokens(gpt2_small, seq_len, batch)
rep_cache.remove_batch_dim()
rep_str = gpt2_small.to_str_tokens(rep_tokens)
gpt2_small.reset_hooks()
log_probs = get_log_probs(rep_logits, rep_tokens).squeeze()Copy co
After running the model, we analyze the log probabilities of the predicted tokens for both halves of the repeated sequences. We observed a mean log probability of -17.270 for the first half and -19.675 for the second half for token sequences varying in indices 177 to 188.
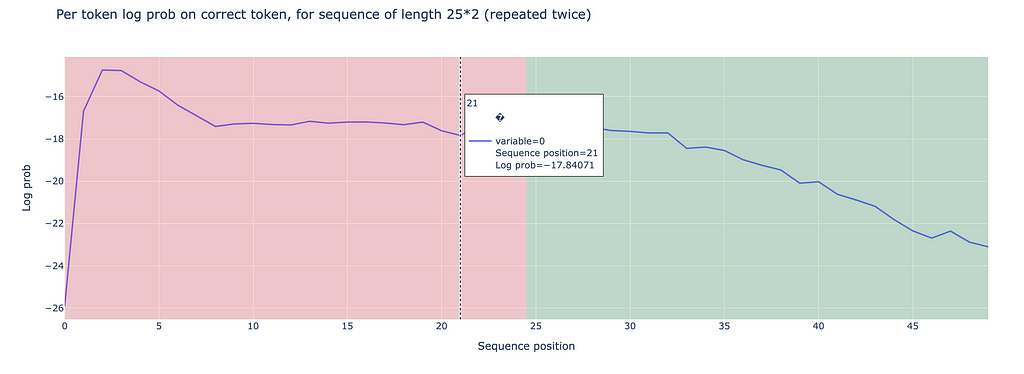
On the other hand, doing the same experiment with a commonly used range of tokens gives different results: When examining token indices 100 to 110, we observe significantly better performance in the second half, with log probabilities of -0.971 compared to -7.327 in the first half.
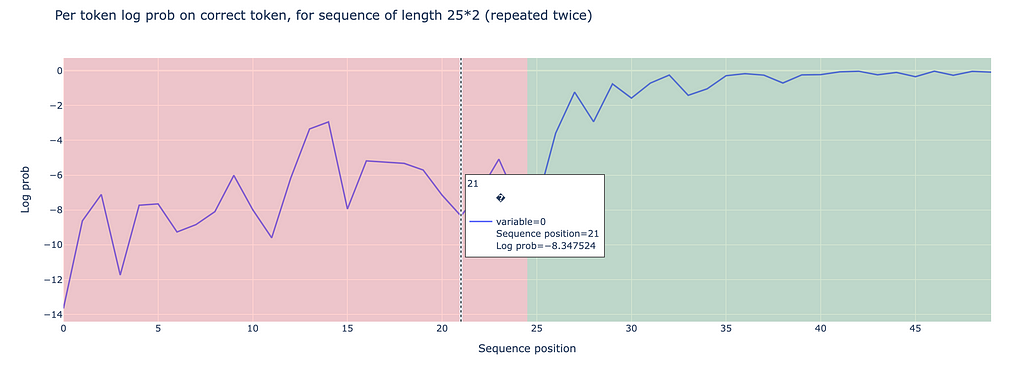
The world of LLM would ideally have less surprise if all unused tokens had significantly negative logits and the model would therefore never produce weird texts.
The reality is, unfortunately much more complex. The fact that the creation of the tokenizer and the training of LLM do not happen at the same time lead sometimes to undertrained tokens which are, the the culprits of unexpected behaviors of LLMs.
An example of undertrained tokens is:_SolidGoldMagikarp[1] which was seen sometimes in ChatGPT’s outputs. Now we would like to prove the existence of under-trained tokens in the case of GPT-2 Small.
In our former experiment of reproducing unused tokens within the GPT-2 Small model, we proved that the token “ú” has hardly any chance to be generated by the model.
Now we slice the logits tensor after runing the model to isolate the outputs to the unused token indices ranging from 177 to 188:
sliced_tensor = gpt2_logits[0, :, 177:188]
Interestingly, we have observed that the logit values for some tokens in this “unused” range reached approximately -1.7, which is to say, there is a probability of around 0.18 for some unused tokens being generated.
This finding highlights the model’s possiblity to assign non-negligible probabilities to some unused tokens, despite they are uncommonly used in most of the context.
In recent years, researchers have proposed techniques to automatically identify under-trained tokens in LLMs. Works in this area include those by Watkins and Rumbelow (2023), and Fell (2023) among which one very interesting approach to identifying under-trained tokens involves analyzing the output embeddings E_{out} generated by the model:
The the method computes the average embedding vector of the unused tokens and uses cosine distances to measure how the vector is similar to all tokens’e embedding vector of the model. Tokens with cosine distances close to the mean embeddings are thus marked as candidates of under-trained tokens. Please check more details in [1].
In conclusion, this blog posts discusses the under-trained tokens LLMs. We do some experiments with GPT-2 Small to illustrate that under-trained tokens can unexpectedly affect model outputs, giving sometimes unpredictable and undesirable behaviors. Recent researches propose methods in identifying under-trained tokens accordingly. For those interested in more details of my implementation, you can check my accompanying notebook.
[1] Land, S., & Bartolo, M. (2024). Fishing for Magikarp: Automatically detecting under-trained tokens in large language models. arXiv. https://doi.org/10.48550/arXiv.2405.05417.
[2] Jessica Rumbelow and Matthew Watkins. 2023. SolidGoldMagikarp (plus, prompt generation). Blog Post.
[3] Martin Fell. 2023. A search for more ChatGPT / GPT3.5 / GPT-4 “unspeakable” glitch tokens. Blog post.
Under-trained and Unused tokens in Large Language Models was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Under-trained and Unused tokens in Large Language Models
Go Here to Read this Fast! Under-trained and Unused tokens in Large Language Models
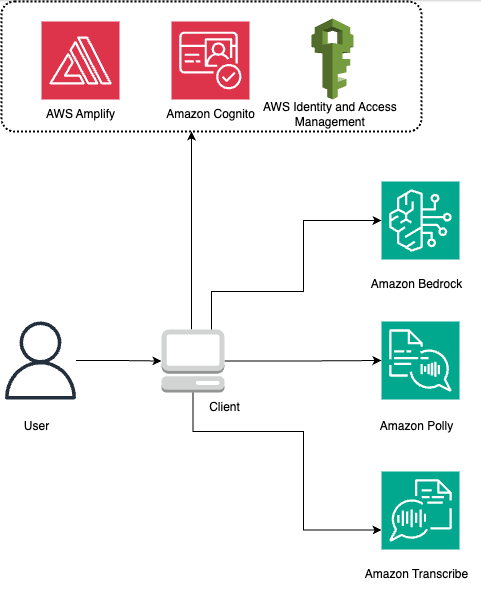
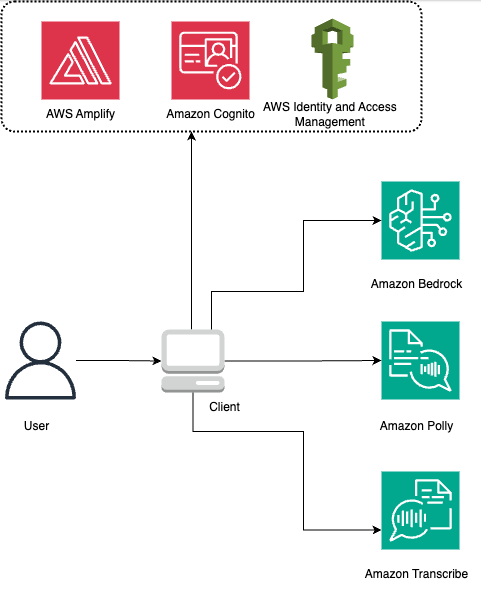
Originally appeared here:
Build a serverless voice-based contextual chatbot for people with disabilities using Amazon Bedrock


Originally appeared here:
Maintain access and consider alternatives for Amazon Monitron
Go Here to Read this Fast! Maintain access and consider alternatives for Amazon Monitron


Rounding out tactics to help you stay competitive as a “full stack” data scientist
Originally appeared here:
Five Engineering Skills Every Data Scientist Should Learn
Go Here to Read this Fast! Five Engineering Skills Every Data Scientist Should Learn