Originally appeared here:
Using Bayesian Modeling to Predict The Champions League
Go Here to Read this Fast! Using Bayesian Modeling to Predict The Champions League

R² (R-squared), also known as the coefficient of determination, is widely used as a metric to evaluate the performance of regression models. It is commonly used to quantify goodness of fit in statistical modeling, and it is a default scoring metric for regression models both in popular statistical modeling and machine learning frameworks, from statsmodels to scikit-learn.
Despite its omnipresence, there is a surprising amount of confusion on what R² truly means, and it is not uncommon to encounter conflicting information (for example, concerning the upper or lower bounds of this metric, and its interpretation). At the root of this confusion is a “culture clash” between the explanatory and predictive modeling tradition. In fact, in predictive modeling — where evaluation is conducted out-of-sample and any modeling approach that increases performance is desirable — many properties of R² that do apply in the narrow context of explanation-oriented linear modeling no longer hold.
To help navigate this confusing landscape, this post provides an accessible narrative primer to some basic properties of R² from a predictive modeling perspective, highlighting and dispelling common confusions and misconceptions about this metric. With this, I hope to help the reader to converge on a unified intuition of what R² truly captures as a measure of fit in predictive modeling and machine learning, and to highlight some of this metric’s strengths and limitations. Aiming for a broad audience which includes Stats 101 students and predictive modellers alike, I will keep the language simple and ground my arguments into concrete visualizations.
Ready? Let’s get started!
Let’s start from a working verbal definition of R². To keep things simple, let’s take the first high-level definition given by Wikipedia, which is a good reflection of definitions found in many pedagogical resources on statistics, including authoritative textbooks:
the proportion of the variation in the dependent variable that is predictable from the independent variable(s)
Anecdotally, this is also what the vast majority of students trained in using statistics for inferential purposes would probably say, if you asked them to define R². But, as we will see in a moment, this common way of defining R² is the source of many of the misconceptions and confusions related to R². Let’s dive deeper into it.
Calling R² a proportion implies that R² will be a number between 0 and 1, where 1 corresponds to a model that explains all the variation in the outcome variable, and 0 corresponds to a model that explains no variation in the outcome variable. Note: your model might also include no predictors (e.g., an intercept-only model is still a model), that’s why I am focusing on variation predicted by a model rather than by independent variables.
Let’s verify if this intuition on the range of possible values is correct. To do so, let’s recall the mathematical definition of R²:
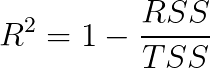
Here, RSS is the residual sum of squares, which is defined as:
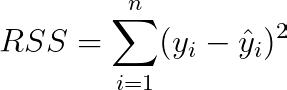
This is simply the sum of squared errors of the model, that is the sum of squared differences between true values y and corresponding model predictions ŷ.
On the other hand, TSS, the total sum of squares, is defined as follows:
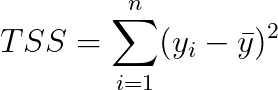
As you might notice, this term has a similar “form” than the residual sum of squares, but this time, we are looking at the squared differences between the true values of the outcome variables y and the mean of the outcome variable ȳ. This is technically the variance of the outcome variable. But a more intuitive way to look at this in a predictive modeling context is the following: this term is the residual sum of squares of a model that always predicts the mean of the outcome variable. Hence, the ratio of RSS and TSS is a ratio between the sum of squared errors of your model, and the sum of squared errors of a “reference” model predicting the mean of the outcome variable.
With this in mind, let’s go on to analyse what the range of possible values for this metric is, and to verify our intuition that these should, indeed, range between 0 and 1.
As we have seen so far, R² is computed by subtracting the ratio of RSS and TSS from 1. Can this ever be higher than 1? Or, in other words, is it true that 1 is the largest possible value of R²? Let’s think this through by looking back at the formula.
The only scenario in which 1 minus something can be higher than 1 is if that something is a negative number. But here, RSS and TSS are both sums of squared values, that is, sums of positive values. The ratio of RSS and TSS will thus always be positive. The largest possible R² must therefore be 1.
Now that we have established that R² cannot be higher than 1, let’s try to visualize what needs to happen for our model to have the maximum possible R². For R² to be 1, RSS / TSS must be zero. This can happen if RSS = 0, that is, if the model predicts all data points perfectly.

In practice, this will never happen, unless you are wildly overfitting your data with an overly complex model, or you are computing R² on a ridiculously low number of data points that your model can fit perfectly. All datasets will have some amount of noise that cannot be accounted for by the data. In practice, the largest possible R² will be defined by the amount of unexplainable noise in your outcome variable.
So far so good. If the largest possible value of R² is 1, we can still think of R² as the proportion of variation in the outcome variable explained by the model. But let’s now move on to looking at the lowest possible value. If we buy into the definition of R² we presented above, then we must assume that the lowest possible R² is 0.
When is R² = 0? For R² to be null, RSS/TSS must be equal to 1. This is the case if RSS = TSS, that is, if the sum of squared errors of our model is equal to the sum of squared errors of a model predicting the mean. If you are better off just predicting the mean, then your model is really not doing a terribly good job. There are infinitely many reasons why this can happen, one of these being an issue with your choice of model — if, for example, if you are trying to model really non-linear data with a linear model. Or it can be a consequence of your data. If your outcome variable is very noisy, then a model predicting the mean might be the best you can do.

But is R² = 0 truly the lowest possible R²? Or, in other words, can R² ever be negative? Let’s look back at the formula. R² < 0 is only possible if RSS/TSS > 1, that is, if RSS > TSS. Can this ever be the case?
This is where things start getting interesting, as the answer to this question depends very much on contextual information that we have not yet specified, namely which type of models we are considering, and which data we are computing R² on. As we will see, whether our interpretation of R² as the proportion of variance explained holds depends on our answer to these questions.
Let’s looks at a concrete case. Let’s generate some data using the following model y = 3 + 2x, and added Gaussian noise.
import numpy as np
x = np.arange(0, 1000, 10)
y = [3 + 2*i for i in x]
noise = np.random.normal(loc=0, scale=600, size=x.shape[0])
true_y = noise + y
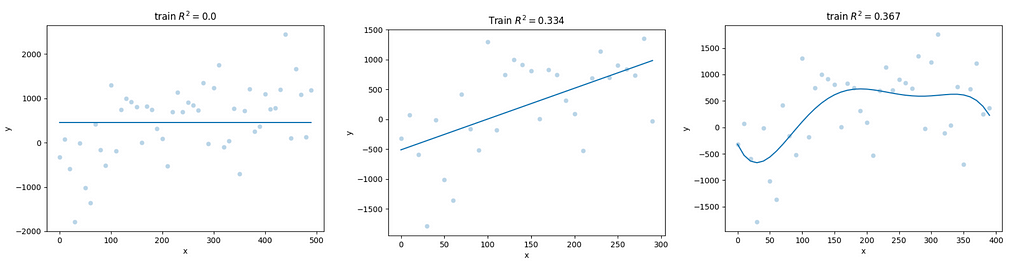
The figure below displays three models that make predictions for y based on values of x for different, randomly sampled subsets of this data. These models are not made-up models, as we will see in a moment, but let’s ignore this right now. Let’s focus simply on the sign of their R².
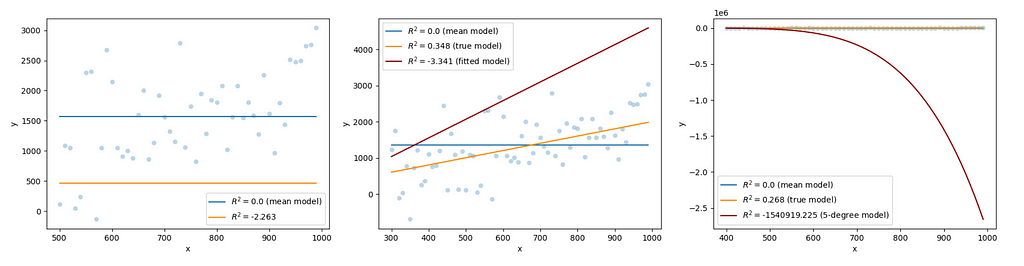
Let’s start from the first model, a simple model that predicts a constant, which in this case is lower than the mean of the outcome variable. Here, our RSS will be the sum of squared distances between each of the dots and the orange line, while TSS will be the sum of squared distances between each of the dots and the blue line (the mean model). It is easy to see that for most of the data points, the distance between the dots and the orange line will be higher than the distance between the dots and the blue line. Hence, our RSS will be higher than our TSS. If this is the case, we will have RSS/TSS > 1, and, therefore: 1 — RSS/TSS < 0, that is, R²<0.
In fact, if we compute R² for this model on this data, we obtain R² = -2.263. If you want to check that it is in fact realistic, you can run the code below (due to randomness, you will likely get a similarly negative value, but not exactly the same value):
from sklearn.metrics import r2_score
# get a subset of the data
x_tr, x_ts, y_tr, y_ts = train_test_split(x, true_y, train_size=.5)
# compute the mean of one of the subsets
model = np.mean(y_tr)
# evaluate on the subset of data that is plotted
print(r2_score(y_ts, [model]*y_ts.shape[0]))
Let’s now move on to the second model. Here, too, it is easy to see that distances between the data points and the red line (our target model) will be larger than distances between data points and the blue line (the mean model). In fact, here: R²= -3.341. Note that our target model is different from the true model (the orange line) because we have fitted it on a subset of the data that also includes noise. We will return to this in the next paragraph.
Finally, let’s look at the last model. Here, we fit a 5-degree polynomial model to a subset of the data generated above. The distance between data points and the fitted function, here, is dramatically higher than the distance between the data points and the mean model. In fact, our fitted model yields R² = -1540919.225.
Clearly, as this example shows, models can have a negative R². In fact, there is no limit to how low R² can be. Make the model bad enough, and your R² can approach minus infinity. This can also happen with a simple linear model: further increase the value of the slope of the linear model in the second example, and your R² will keep going down. So, where does this leave us with respect to our initial question, namely whether R² is in fact that proportion of variance in the outcome variable that can be accounted for by the model?
Well, we don’t tend to think of proportions as arbitrarily large negative values. If are really attached to the original definition, we could, with a creative leap of imagination, extend this definition to covering scenarios where arbitrarily bad models can add variance to your outcome variable. The inverse proportion of variance added by your model (e.g., as a consequence of poor model choices, or overfitting to different data) is what is reflected in arbitrarily low negative values.
But this is more of a metaphor than a definition. Literary thinking aside, the most literal and most productive way of thinking about R² is as a comparative metric, which says something about how much better (on a scale from 0 to 1) or worse (on a scale from 0 to infinity) your model is at predicting the data compared to a model which always predicts the mean of the outcome variable.
Importantly, what this suggests, is that while R² can be a tempting way to evaluate your model in a scale-independent fashion, and while it might makes sense to use it as a comparative metric, it is a far from transparent metric. The value of R² will not provide explicit information of how wrong your model is in absolute terms; the best possible value will always be dependent on the amount of noise present in the data; and good or bad R² can come about from a wide variety of reasons that can be hard to disambiguate without the aid of additional metrics.
A very legitimate objection, here, is whether any of the scenarios displayed above is actually plausible. I mean, which modeller in their right mind would actually fit such poor models to such simple data? These might just look like ad hoc models, made up for the purpose of this example and not actually fit to any data.
This is an excellent point, and one that brings us to another crucial point related to R² and its interpretation. As we highlighted above, all these models have, in fact, been fit to data which are generated from the same true underlying function as the data in the figures. This corresponds to the practice, foundational to predictive modeling, of splitting data intro a training set and a test set, where the former is used to estimate the model, and the latter for evaluation on unseen data — which is a “fairer” proxy for how well the model generally performs in its prediction task.
In fact, if we display the models introduced in the previous section against the data used to estimate them, we see that they are not unreasonable models in relation to their training data. In fact, R² values for the training set are, at least, non-negative (and, in the case of the linear model, very close to the R² of the true model on the test data).
Why, then, is there such a big difference between the previous data and this data? What we are observing are cases of overfitting. The model is mistaking sample-specific noise in the training data for signal and modeling that — which is not at all an uncommon scenario. As a result, models’ predictions on new data samples will be poor.
Avoiding overfitting is perhaps the biggest challenge in predictive modeling. Thus, it is not at all uncommon to observe negative R² values when (as one should always do to ensure that the model is generalizable and robust ) R² is computed out-of-sample, that is, on data that differ “randomly” from those on which the model was estimated.
Thus, the answer to the question posed in the title of this section is, in fact, a resounding yes: negative R² do happen in common modeling scenarios, even when models have been properly estimated. In fact, they happen all the time.
If R² is not a proportion, and its interpretation as variance explained clashes with some basic facts about its behavior, do we have to conclude that our initial definition is wrong? Are Wikipedia and all those textbooks presenting a similar definition wrong? Was my Stats 101 teacher wrong? Well. Yes, and no. It depends hugely on the context in which R² is presented, and on the modeling tradition we are embracing.
If we simply analyse the definition of R² and try to describe its general behavior, regardless of which type of model we are using to make predictions, and assuming we will want to compute this metrics out-of-sample, then yes, they are all wrong. Interpreting R² as the proportion of variance explained is misleading, and it conflicts with basic facts on the behavior of this metric.
Yet, the answer changes slightly if we constrain ourselves to a narrower set of scenarios, namely linear models, and especially linear models estimated with least squares methods. Here, R² will behave as a proportion. In fact, it can be shown that, due to properties of least squares estimation, a linear model can never do worse than a model predicting the mean of the outcome variable. Which means, that a linear model can never have a negative R² — or at least, it cannot have a negative R² on the same data on which it was estimated (a debatable practice if you are interested in a generalizable model). For a linear regression scenario with in-sample evaluation, the definition discussed can therefore be considered correct. Additional fun fact: this is also the only scenario where R² is equivalent to the squared correlation between model predictions and the true outcomes.
The reason why many misconceptions about R² arise is that this metric is often first introduced in the context of linear regression and with a focus on inference rather than prediction. But in predictive modeling, where in-sample evaluation is a no-go and linear models are just one of many possible models, interpreting R² as the proportion of variation explained by the model is at best unproductive, and at worst deeply misleading.
We have touched upon quite a few points, so let’s sum them up. We have observed that:
Given all these caveats, should we still use R²? Or should we give up?
Here, we enter the territory of more subjective observations. In general, if you are doing predictive modeling and you want to get a concrete sense for how wrong your predictions are in absolute terms, R² is not a useful metric. Metrics like MAE or RMSE will definitely do a better job in providing information on the magnitude of errors your model makes. This is useful in absolute terms but also in a model comparison context, where you might want to know by how much, concretely, the precision of your predictions differs across models. If knowing something about precision matters (it hardly ever does not), you might at least want to complement R² with metrics that says something meaningful about how wrong each of your individual predictions is likely to be.
More generally, as we have highlighted, there are a number of caveats to keep in mind if you decide to use R². Some of these concern the “practical” upper bounds for R² (your noise ceiling), and its literal interpretation as a relative, rather than absolute measure of fit compared to the mean model. Furthermore, good or bad R² values, as we have observed, can be driven by many factors, from overfitting to the amount of noise in your data.
On the other hand, while there are very few predictive modeling contexts where I have found R² particularly informative in isolation, having a measure of fit relative to a “dummy” model (the mean model) can be a productive way to think critically about your model. Unrealistically high R² on your training set, or a negative R² on your test set might, respectively, help you entertain the possibility that you might be going for an overly complex model or for an inappropriate modeling approach (e.g., a linear model for non-linear data), or that your outcome variable might contain, mostly, noise. This is, again, more of a “pragmatic” personal take here, but while I would resist fully discarding R² (there aren’t many good global and scale-independent measures of fit), in a predictive modeling context I would consider it most useful as a complement to scale-dependent metrics such as RMSE/MAE, or as a “diagnostic” tool, rather than a target itself.
R² is everywhere. Yet, especially in fields that are biased towards explanatory, rather than predictive modelling traditions, many misconceptions about its interpretation as a model evaluation tool flourish and persist.
In this post, I have tried to provide a narrative primer to some basic properties of R² in order to dispel common misconceptions, and help the reader get a grasp of what R² generally measures beyond the narrow context of in-sample evaluation of linear models.
Far from being a complete and definitive guide, I hope this can be a pragmatic and agile resource to clarify some very justified confusion. Cheers!
Unless otherwise states in the caption, images in this article are by the author
Interpreting R²: a Narrative Guide for the Perplexed was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Interpreting R²: a Narrative Guide for the Perplexed
Go Here to Read this Fast! Interpreting R²: a Narrative Guide for the Perplexed



In a previous post I did a little PoC to see if I could use OpenAI’s Clip model to build a semantic book search. It worked surprisingly well, in my opinion, but I couldn’t help wondering if it would be better with more data. The previous version used only about 3.5k books, but there are millions in the Openlibrary data set, and I thought it was worthwhile to try adding more options to the search space.
However, the full dataset is about 40GB, and trying to handle that much data on my little laptop, or even in a Colab notebook was a bit much, so I had to figure out a pipeline that could manage filtering and embedding a larger data set.
TLDR; Did it improve the search? I think it did! We 15x’ed the data, which gives the search much more to work with. Its not perfect, but I thought the results were fairly interesting; although I haven’t done a formal accuracy measure.
This was one example I couldn’t get to work no matter how I phrased it in the last iteration, but works fairly well in the version with more data.
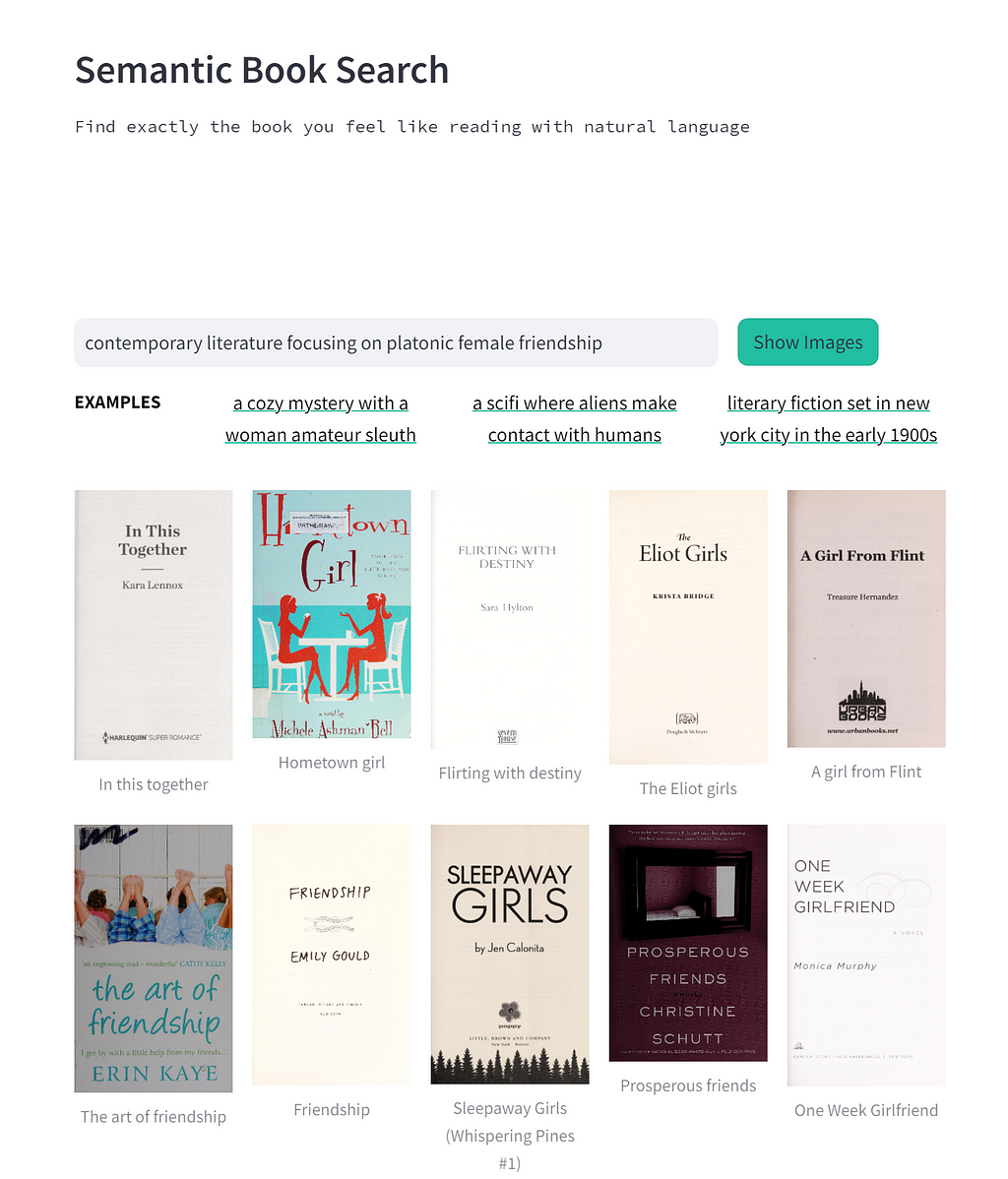
If you’re curious you can try it out in Colab!
Overall, it was an interesting technical journey, with a lot of roadblocks and learning opportunities along the way. The tech stack still includes the OpenAI Clip model, but this time I leverage Apache Spark and AWS EMR to run the embedding pipeline.
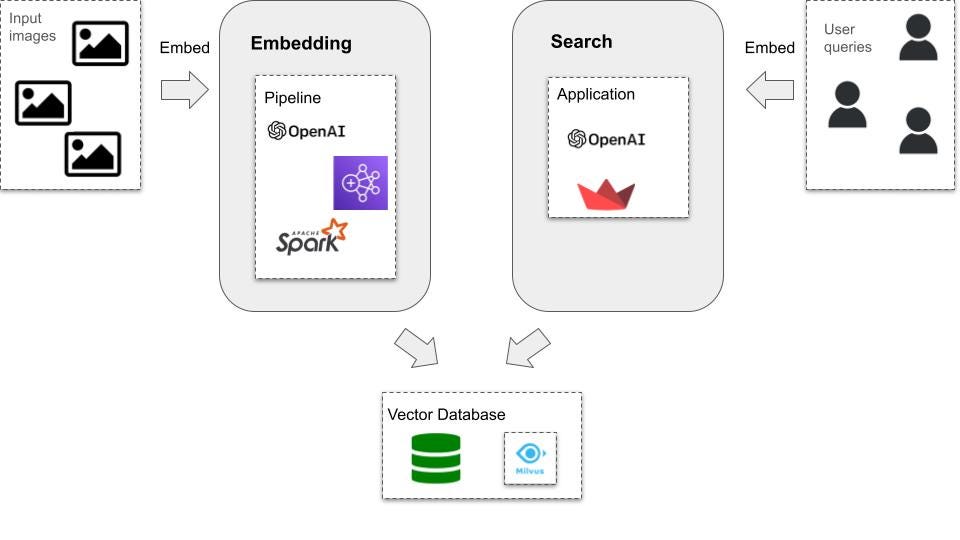
This seemed like a good opportunity to use Spark, as it allows us to parallelize the embedding computation.
I decided to run the pipeline in EMR Serverless, which is a fairly new AWS offering that provides a serverless environment for EMR and manages scaling resources automatically. I felt it would work well for this use case — as opposed to spinning up an EMR on EC2 cluster — because this is a fairly ad-hoc project, I’m paranoid about cluster costs, and initially I was unsure about what resources the job would require. EMR Serverless makes it pretty easy to experiment with job parameters.
Below is the full process I went through to get everything up and running. I imagine there are better ways to manage certain steps, this is just what ended up working for me, so if you have thoughts or opinions, please do share!
The initial step was writing the Spark job(s). The full pipeline is broken out into two stages, the first takes in the initial data set and filters for recent fiction (within the last 10 years). This resulted in about 250k books, and around 70k with cover images available to download and embed in the second stage.
First we pull out the relevant columns from the raw data file.
Then do some general data transformation on data types, and filter out everything but English fiction with more than 100 pages.
The second stage grabs the first stage’s output dataset, and runs the images through the Clip model, downloaded from Hugging Face. The important step here is turning the various functions that we need to apply to the data into Spark UDFs. The main one of interest is get_image_embedding, which takes in the image and returns the embedding
We register it as a UDF:
And call that UDF on the dataset:
As a last, optional, step in the code, we can setup a vector database, in this case Milvus, to load and query from. Note, I did not do this as part of the cloud job for this project, as I pickled my embeddings to use without having to keep a cluster up and running indefinitely. However, it is fairly simple to setup Milvus and load a Spark Dataframe to a collection.
First, create a collection with an index on the image embedding column that the database can use for the search.
Then we can access the collection in the Spark script, and load the embeddings into it from the final Dataframe.
Finally, we can simply embed the search text with the same method used in the UDF above, and hit the database with the embeddings. The database does the heavy lifting of figuring out the best matches
Prerequisites
Now there’s a bit of setup to go through in order to run these jobs on EMR Serverless.
As prerequisites we need:
There are great descriptions of the roles and permissions policies, as well as a general outline of how to get up and running with EMR Serverless in the AWS docs here: Getting started with Amazon EMR Serverless
Next we have to setup an EMR Studio: Create an EMR Studio
Accessing the web via an Internet Gateway
Another bit of setup that’s specific to this particular job is that we have to allow the job to reach out to the Internet, which the EMR application is not able to do by default. As we saw in the script, the job needs to access both the images to embed, as well as Hugging Face to download the model configs and weights.
Note: There are likely more efficient ways to handle the model than downloading it to each worker (broadcasting it, storing it somewhere locally in the system, etc), but in this case, for a single run through the data, this is sufficient.
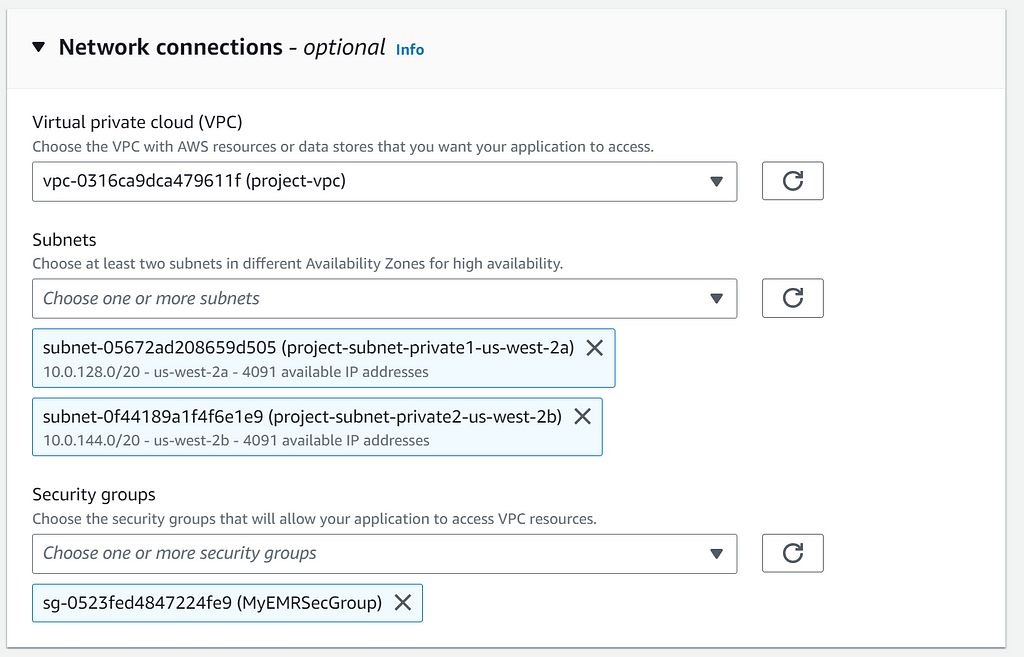
Anyway, allowing the machine the Spark job is running on to reach out to the Internet requires VPC with private subnets that have NAT gateways. All of this setup starts with accessing AWS VPC interface -> Create VPC -> selecting VPC and more -> selecting option for at least on NAT gateway -> clicking Create VPC.
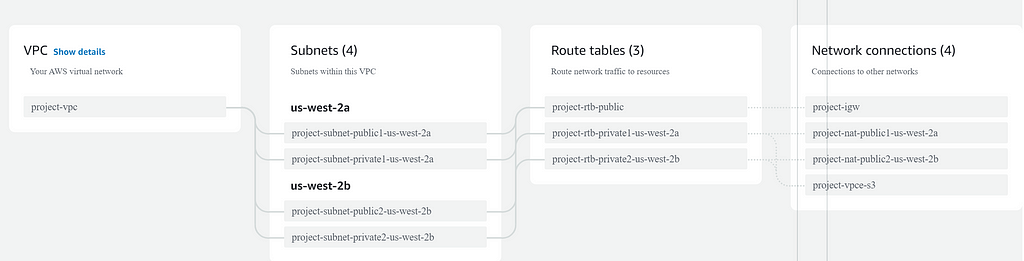
The VPC takes a few minutes to set up. Once that is done we also need to create a security group in the security group interface, and attach the VPC we just created.
Creating the EMR Serverless application
Now for the EMR Serverless application that will submit the job! Creating and launching an EMR studio should open a UI that offers a few options including creating an application. In the create application UI, select Use Custom settings -> Network settings. Here is where the VPC, the two private subnets, and the security group come into play.
Building a virtual environment
Finally, the environment doesn’t come with many libraries, so in order to add additional Python dependencies we can either use native Python or create and package a virtual environment: Using Python libraries with EMR Serverless.
I went the second route, and the easiest way to do this is with Docker, as it allows us to build the virtual environment within the Amazon Linux distribution that’s running the EMR jobs (doing it in any other distribution or OS can become incredibly messy).
Another warning: be careful to pick the version of EMR that corresponds to the version of Python that you are using, and choose package versions accordingly as well.
The Docker process outputs the zipped up virtual environment as pyspark_dependencies.tar.gz, which then goes into the S3 bucket along with the job scripts.
We can then send this packaged environment along with the rest of the Spark job configurations
Nice! We have the job script, the environmental dependencies, gateways, and an EMR application, we get to submit the job! Not so fast! Now comes the real fun, Spark tuning.
As previously mentioned, EMR Serverless scales automatically to handle our workload, which typically would be great, but I found (obvious in hindsight) that it was unhelpful for this particular use case.
A few tens of thousands of records is not at all “big data”; Spark wants terabytes of data to work through, and I was just sending essentially a few thousand image urls (not even the images themselves). Left to its own devices, EMR Serverless will send the job to one node to work through on a single thread, completely defeating the purpose of parallelization.
Additionally, while embedding jobs take in a relatively small amount of data, they expand it significantly, as the embeddings are quite large (512 in the case of Clip). Even if you leave that one node to churn away for a few days, it’ll run out of memory long before it finishes working through the full set of data.
In order to get it to run, I experimented with a few Spark properties so that I could use large machines in the cluster, but split the data into very small partitions so that each core would have just a bit to work through and output:
You’ll have to tweak these depending on the particular nature of the your data, and embedding still isn’t a speedy process, but it was able to work through my data.
As with my previous post the results certainly aren’t perfect, and by no means a replacement for solid book recommendations from other humans! But that being said there were some spot on answers to a number of my searches, which I thought was pretty cool.
If you want to play around with the app yourself, its in Colab, and the full code for the pipeline is in Github!
Building a Semantic Book Search: Scale an Embedding Pipeline with Apache Spark and AWS EMR… was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Building a Semantic Book Search: Scale an Embedding Pipeline with Apache Spark and AWS EMR…

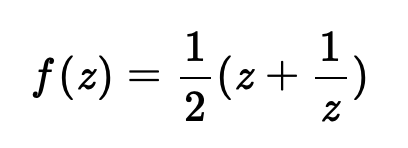
Today I was pouring through Complex Variables and Analytic Functions by the esteemed Fornberg and Piret, trying my best to wrap my mind around how complex-valued functions behave. Mentally vizualization such functions is extra difficult since they take a real and an imaginary input, and outputs two components as well. Therefore, a single 3-D plot is not sufficient to see how the function behaves. Rather, we have to split such a visualization into separate plots of the imaginary and real parts, or alternatively by magnitude and argument, or angle.
I wanted to be able to play around with any function I could think of, drag and zoom around its plots, and explore it in visual detail to understand how it resulted from the equation. For such a task, Wolfram Mathematica is an excellent starting tool.
plotComplexFunction[f_]:=Module[{z,rePlot,imPlot,magPlot,phasePlot},z=x+I y;
rePlot = Plot3D[Re[f[z]],{x,-2,2},{y,-2,2},AxesLabel->{"Re(z)","Im(z)","Re(f(z))"},Mesh->None];
imPlot = Plot3D[Im[f[z]],{x,-2,2},{y,-2,2},
AxesLabel->{"Re(z)","Im(z)","Im(f(z))"},
Mesh->None];
magPlot = Plot3D[Abs[f[z]], {x, -2, 2}, {y, -2, 2},
AxesLabel -> {"Re(z)", "Im(z)", "Abs(f(z))"},
Mesh -> None,
ColorFunction -> Function[{x, y, z}, ColorData["Rainbow"][Rescale[Arg[x + I y], {-Pi, Pi}]]],
ColorFunctionScaling -> False];
phasePlot=DensityPlot[Arg[f[z]],{x,-2,2},{y,-2,2},
ColorFunction->"Rainbow",
PlotLegends->Automatic,
AxesLabel->{"Re(z)","Im(z)"},
PlotLabel->"Phase"];
GraphicsGrid[{{rePlot,imPlot},{magPlot,phasePlot}},ImageSize->800]];
f[z_]:=(1/2)*(z+1/z);
plotComplexFunction[f]
https://github.com/dreamchef/complex-functions-visualization
https://github.com/dreamchef/complex-functions-visualization
I wrote the above Mathematica code to produce a grid of plots showing the function in both ways just described. On the top, the imaginary and real parts of the function
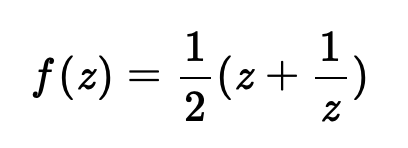
are shown, and on the bottom, and the magnitude, and the phase shown in color:
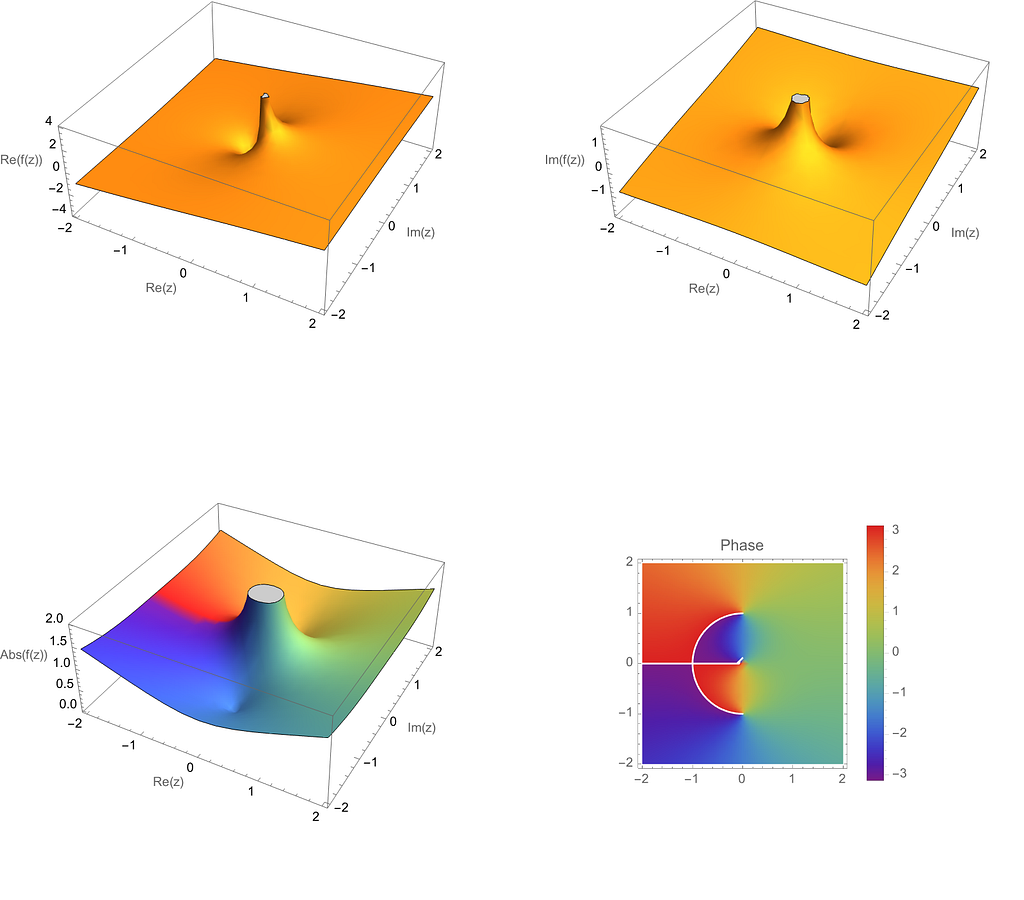
After playing around with a few functions using this code and convincing myself they made sense, I was interested in getting the same functionality in Python, to connect it to my other mathematical programming projects.
I found an excellent project on GitHub (https://github.com/artmenlope/complex-plotting-tools) which I decided to use as a starting point, and potentially contribute to in the future. The repo provided a very easy interface for plotting complex-valued functions in a variety of ways. Thanks https://github.com/artmenlope! For example, after importing numpy, matplotlib, and the repo’s cplotting_tools module defining the function and calling cplt.complex_plot3D(x,y,f,log_mode=False) produces the following:
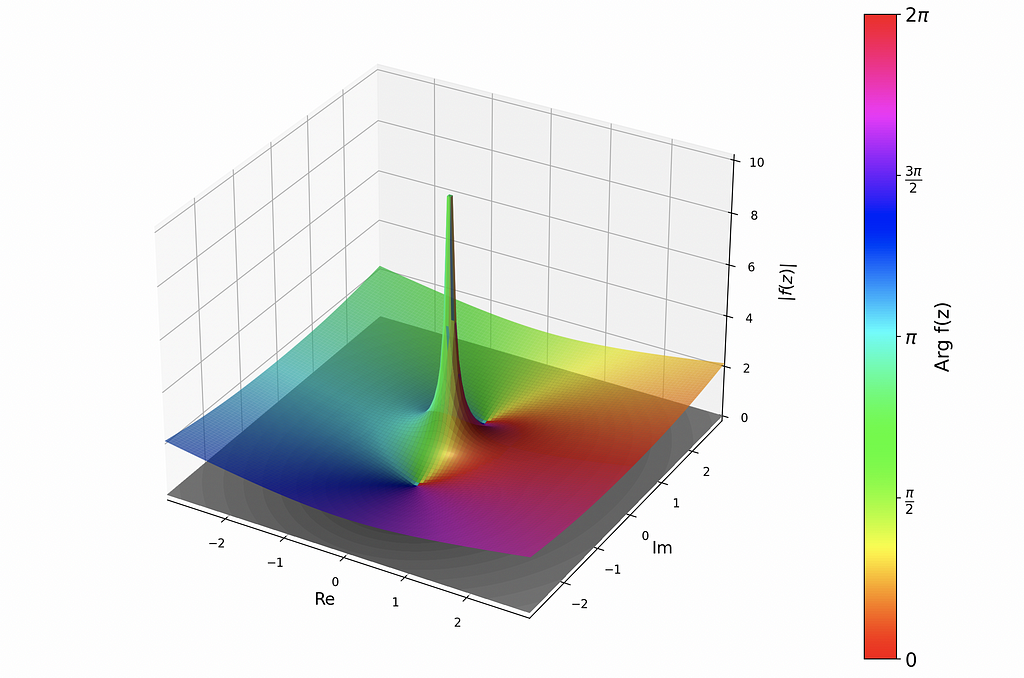
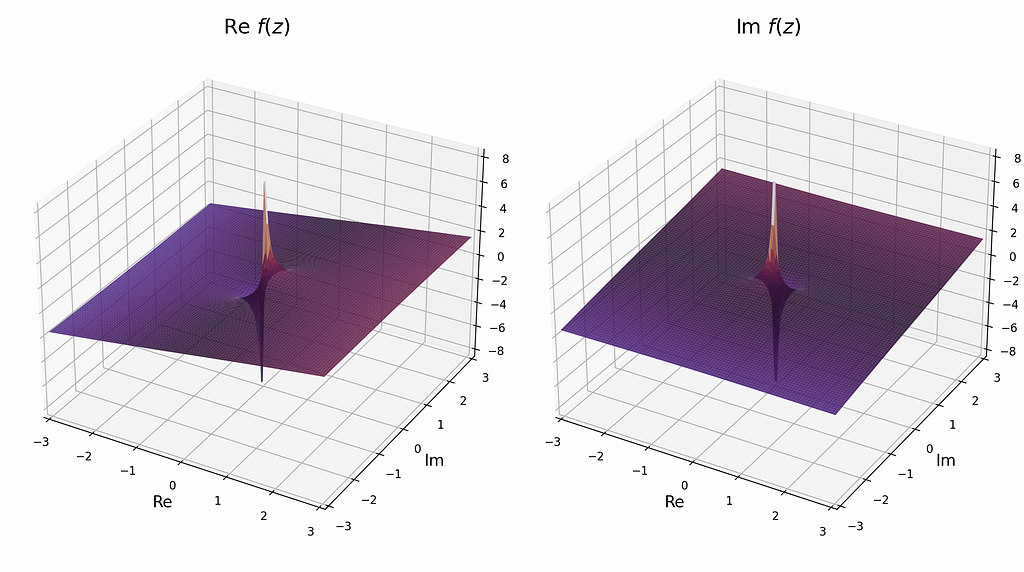
These are all for the same f(z) as above. To view the side-by-side imaginary and real parts of the function, use cplot.plot_re_im(x,y,f,camp=”twilight”,contour=False,alpha=0.9:
Additionally, the library provides other cool ways to study functions, including a stream plot:
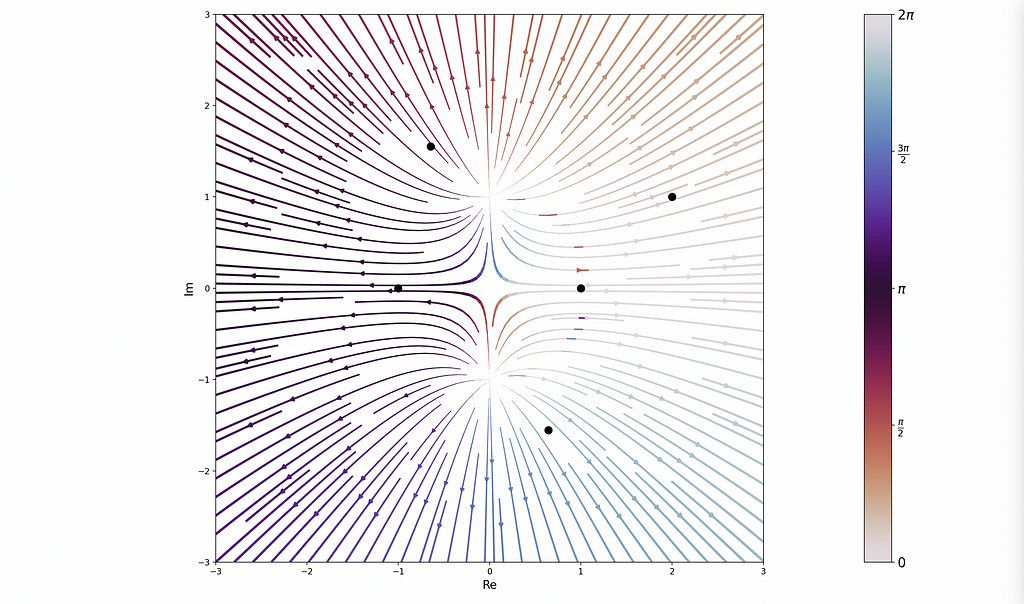
The library shows a lot of promise and is relatively easy to use! It does require a pts variable to be defined that encodes the poles and zeros of the given function. Wolfram does not require this because it computes the locations of these points under the hood. It would save a lot of effort for the user if complex-plotting-tools had this functionality as well. I plan to implement this is into the module in the near future.
In the meantime, have fun plotting with Wolfram and Python, and share your thoughts and questions in comments below, connect with me on LinkedIn or collaborate with me on GitHub!
Unless otherwise noted, all images were created by the author.
Visualizing Complex-Valued Functions Using Python and Mathematica was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Visualizing Complex-Valued Functions Using Python and Mathematica
Go Here to Read this Fast! Visualizing Complex-Valued Functions Using Python and Mathematica
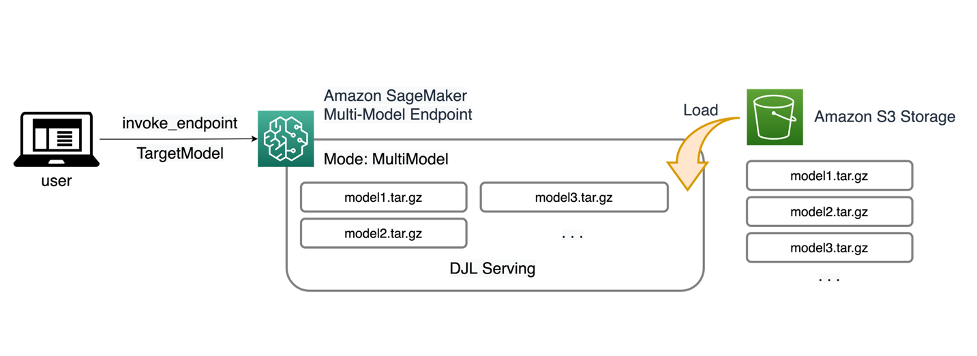

Originally appeared here:
Run ML inference on unplanned and spiky traffic using Amazon SageMaker multi-model endpoints


Originally appeared here:
Use Amazon Titan models for image generation, editing, and searching
Go Here to Read this Fast! Use Amazon Titan models for image generation, editing, and searching

Originally appeared here:
Build a contextual chatbot application using Knowledge Bases for Amazon Bedrock
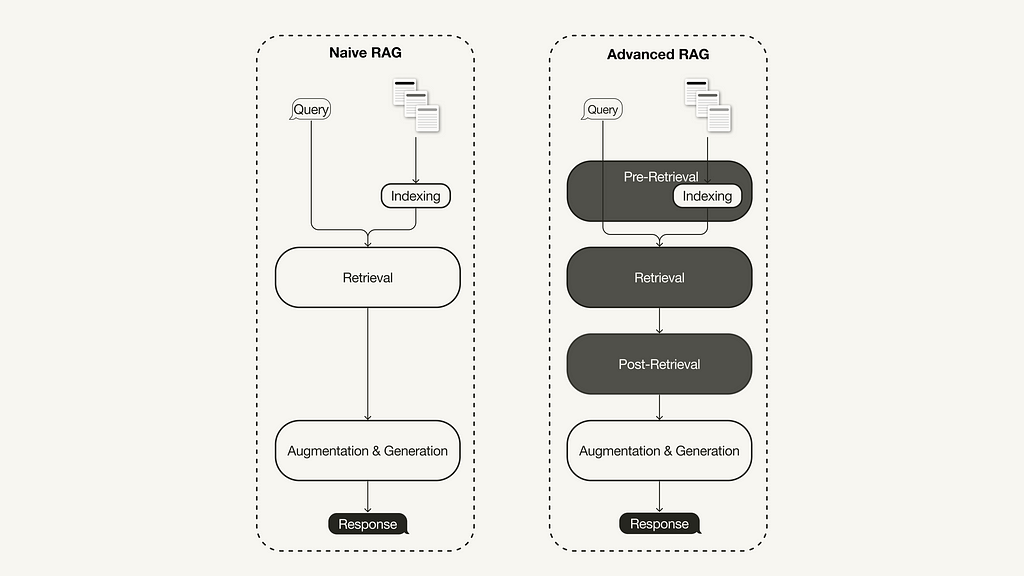
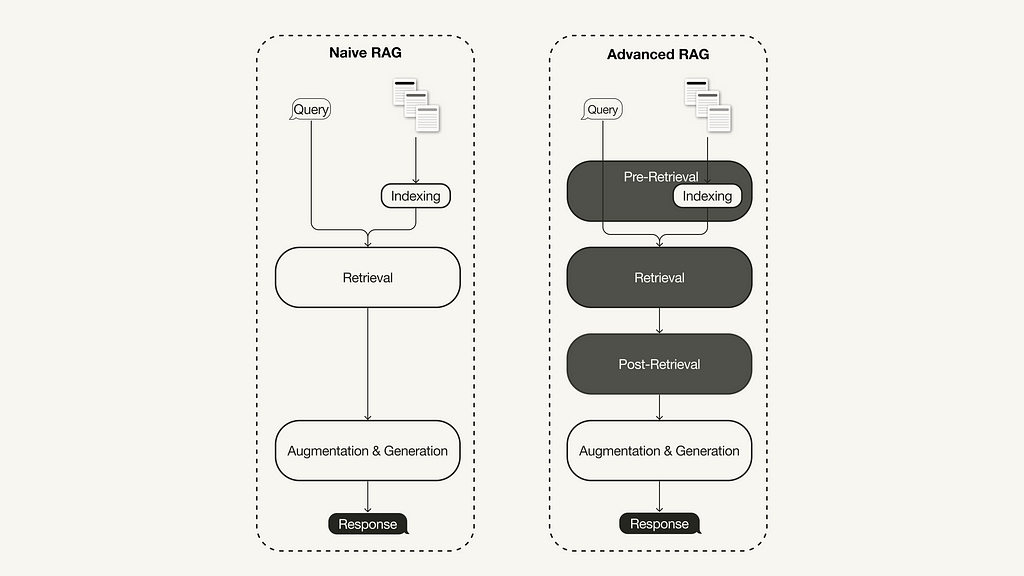

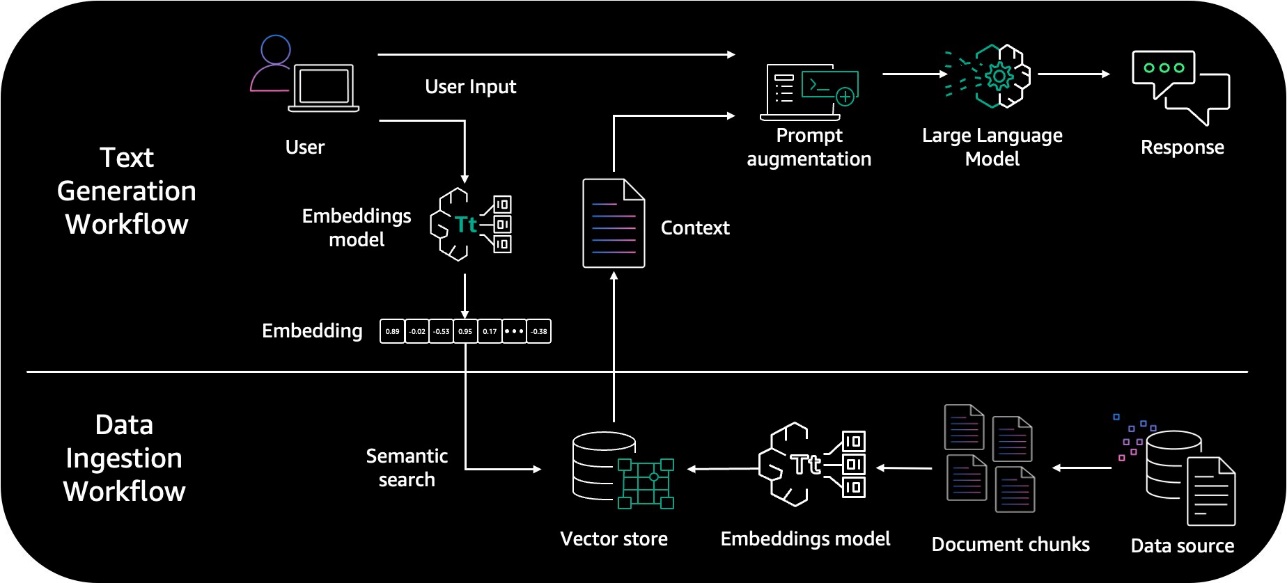
A recent survey on Retrieval-Augmented Generation (RAG) [1] summarized three recently evolved paradigms:
The advanced RAG paradigm comprises of a set of techniques targeted at addressing known limitations of naive RAG. This article first discusses these techniques, which can be categorized into pre-retrieval, retrieval, and post-retrieval optimizations.
In the second half, you will learn how to implement a naive RAG pipeline using Llamaindex in Python, which will then be enhanced to an advanced RAG pipeline with a selection of the following advanced RAG techniques:
This article focuses on the advanced RAG paradigm and its implementation. If you are unfamiliar with the fundamentals of RAG, you can catch up on it here:
Retrieval-Augmented Generation (RAG): From Theory to LangChain Implementation
With the recent advancements in the RAG domain, advanced RAG has evolved as a new paradigm with targeted enhancements to address some of the limitations of the naive RAG paradigm. As summarized in a recent survey [1], advanced RAG techniques can be categorized into pre-retrieval, retrieval, and post-retrieval optimizations.
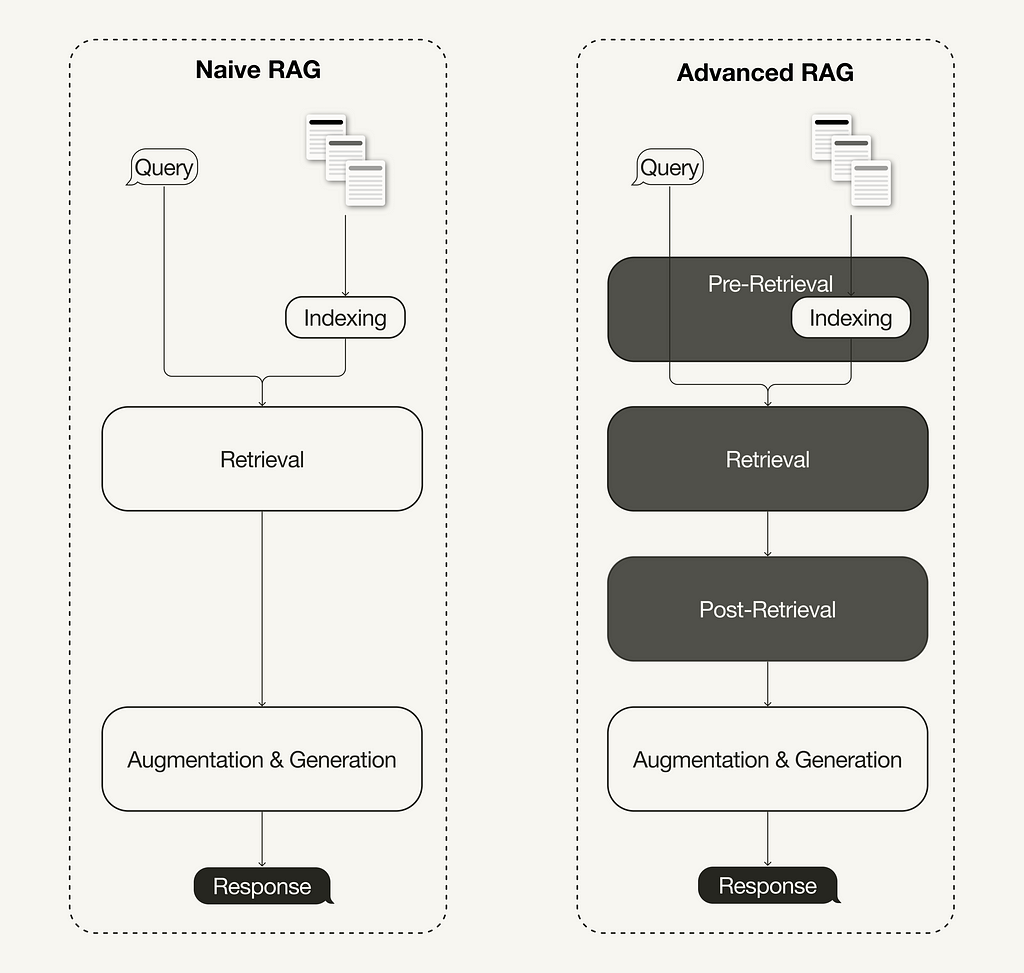
Pre-retrieval optimizations focus on data indexing optimizations as well as query optimizations. Data indexing optimization techniques aim to store the data in a way that helps you improve retrieval efficiency, such as [1]:
Additionally, pre-retrieval techniques aren’t limited to data indexing and can cover techniques at inference time, such as query routing, query rewriting, and query expansion.
The retrieval stage aims to identify the most relevant context. Usually, the retrieval is based on vector search, which calculates the semantic similarity between the query and the indexed data. Thus, the majority of retrieval optimization techniques revolve around the embedding models [1]:
There are also other retrieval techniques besides vector search, such as hybrid search, which often refers to the concept of combining vector search with keyword-based search. This retrieval technique is beneficial if your retrieval requires exact keyword matches.
Improving Retrieval Performance in RAG Pipelines with Hybrid Search
Additional processing of the retrieved context can help address issues such as exceeding the context window limit or introducing noise, thus hindering the focus on crucial information. Post-retrieval optimization techniques summarized in the RAG survey [1] are:
For additional ideas on how to improve the performance of your RAG pipeline to make it production-ready, continue reading here:
A Guide on 12 Tuning Strategies for Production-Ready RAG Applications
This section discusses the required packages and API keys to follow along in this article.
This article will guide you through implementing a naive and an advanced RAG pipeline using LlamaIndex in Python.
pip install llama-index
In this article, we will be using LlamaIndex v0.10. If you are upgrading from an older LlamaIndex version, you need to run the following commands to install and run LlamaIndex properly:
pip uninstall llama-index
pip install llama-index --upgrade --no-cache-dir --force-reinstall
LlamaIndex offers an option to store vector embeddings locally in JSON files for persistent storage, which is great for quickly prototyping an idea. However, we will use a vector database for persistent storage since advanced RAG techniques aim for production-ready applications.
Since we will need metadata storage and hybrid search capabilities in addition to storing the vector embeddings, we will use the open source vector database Weaviate (v3.26.2), which supports these features.
pip install weaviate-client llama-index-vector-stores-weaviate
We will be using Weaviate embedded, which you can use for free without registering for an API key. However, this tutorial uses an embedding model and LLM from OpenAI, for which you will need an OpenAI API key. To obtain one, you need an OpenAI account and then “Create new secret key” under API keys.
Next, create a local .env file in your root directory and define your API keys in it:
OPENAI_API_KEY="<YOUR_OPENAI_API_KEY>"
Afterwards, you can load your API keys with the following code:
# !pip install python-dotenv
import os
from dotenv import load_dotenv,find_dotenv
load_dotenv(find_dotenv())
This section discusses how to implement a naive RAG pipeline using LlamaIndex. You can find the entire naive RAG pipeline in this Jupyter Notebook. For the implementation using LangChain, you can continue in this article (naive RAG pipeline using LangChain).
First, you can define an embedding model and LLM in a global settings object. Doing this means you don’t have to specify the models explicitly in the code again.
from llama_index.embeddings.openai import OpenAIEmbedding
from llama_index.llms.openai import OpenAI
from llama_index.core.settings import Settings
Settings.llm = OpenAI(model="gpt-3.5-turbo", temperature=0.1)
Settings.embed_model = OpenAIEmbedding()
Next, you will create a local directory named data in your root directory and download some example data from the LlamaIndex GitHub repository (MIT license).
!mkdir -p 'data'
!wget '<https://raw.githubusercontent.com/run-llama/llama_index/main/docs/examples/data/paul_graham/paul_graham_essay.txt>' -O 'data/paul_graham_essay.txt'
Afterward, you can load the data for further processing:
from llama_index.core import SimpleDirectoryReader
# Load data
documents = SimpleDirectoryReader(
input_files=["./data/paul_graham_essay.txt"]
).load_data()
As the entire document is too large to fit into the context window of the LLM, you will need to partition it into smaller text chunks, which are called Nodes in LlamaIndex. You can parse the loaded documents into nodes using the SimpleNodeParser with a defined chunk size of 1024.
from llama_index.core.node_parser import SimpleNodeParser
node_parser = SimpleNodeParser.from_defaults(chunk_size=1024)
# Extract nodes from documents
nodes = node_parser.get_nodes_from_documents(documents)
Next, you will build the index that stores all the external knowledge in Weaviate, an open source vector database.
First, you will need to connect to a Weaviate instance. In this case, we’re using Weaviate Embedded, which allows you to experiment in Notebooks for free without an API key. For a production-ready solution, deploying Weaviate yourself, e.g., via Docker or utilizing a managed service, is recommended.
import weaviate
# Connect to your Weaviate instance
client = weaviate.Client(
embedded_options=weaviate.embedded.EmbeddedOptions(),
)
Next, you will build a VectorStoreIndex from the Weaviate client to store your data in and interact with.
from llama_index.core import VectorStoreIndex, StorageContext
from llama_index.vector_stores.weaviate import WeaviateVectorStore
index_name = "MyExternalContext"
# Construct vector store
vector_store = WeaviateVectorStore(
weaviate_client = client,
index_name = index_name
)
# Set up the storage for the embeddings
storage_context = StorageContext.from_defaults(vector_store=vector_store)
# Setup the index
# build VectorStoreIndex that takes care of chunking documents
# and encoding chunks to embeddings for future retrieval
index = VectorStoreIndex(
nodes,
storage_context = storage_context,
)
Lastly, you will set up the index as the query engine.
# The QueryEngine class is equipped with the generator
# and facilitates the retrieval and generation steps
query_engine = index.as_query_engine()
Now, you can run a naive RAG query on your data, as shown below:
# Run your naive RAG query
response = query_engine.query(
"What happened at Interleaf?"
)
In this section, we will cover some simple adjustments you can make to turn the above naive RAG pipeline into an advanced one. This walkthrough will cover the following selection of advanced RAG techniques:
As we will only cover the modifications here, you can find the full end-to-end advanced RAG pipeline in this Jupyter Notebook.
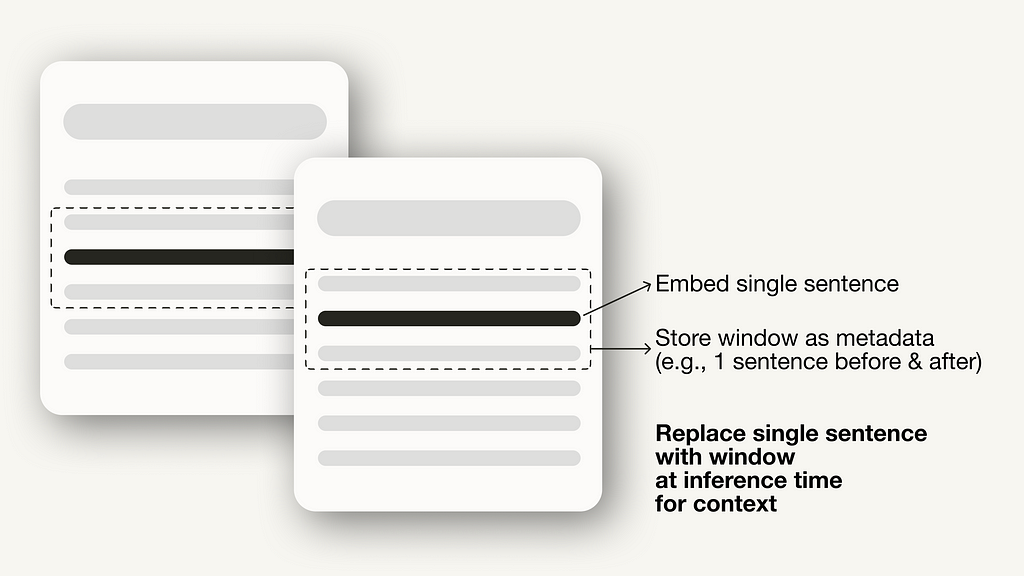
For the sentence window retrieval technique, you need to make two adjustments: First, you must adjust how you store and post-process your data. Instead of the SimpleNodeParser, we will use the SentenceWindowNodeParser.
from llama_index.core.node_parser import SentenceWindowNodeParser
# create the sentence window node parser w/ default settings
node_parser = SentenceWindowNodeParser.from_defaults(
window_size=3,
window_metadata_key="window",
original_text_metadata_key="original_text",
)
The SentenceWindowNodeParser does two things:
During retrieval, the sentence that most closely matches the query is returned. After retrieval, you need to replace the sentence with the entire window from the metadata by defining a MetadataReplacementPostProcessor and using it in the list of node_postprocessors.
from llama_index.core.postprocessor import MetadataReplacementPostProcessor
# The target key defaults to `window` to match the node_parser's default
postproc = MetadataReplacementPostProcessor(
target_metadata_key="window"
)
...
query_engine = index.as_query_engine(
node_postprocessors = [postproc],
)
Implementing a hybrid search in LlamaIndex is as easy as two parameter changes to the query_engine if the underlying vector database supports hybrid search queries. The alpha parameter specifies the weighting between vector search and keyword-based search, where alpha=0 means keyword-based search and alpha=1 means pure vector search.
query_engine = index.as_query_engine(
...,
vector_store_query_mode="hybrid",
alpha=0.5,
...
)
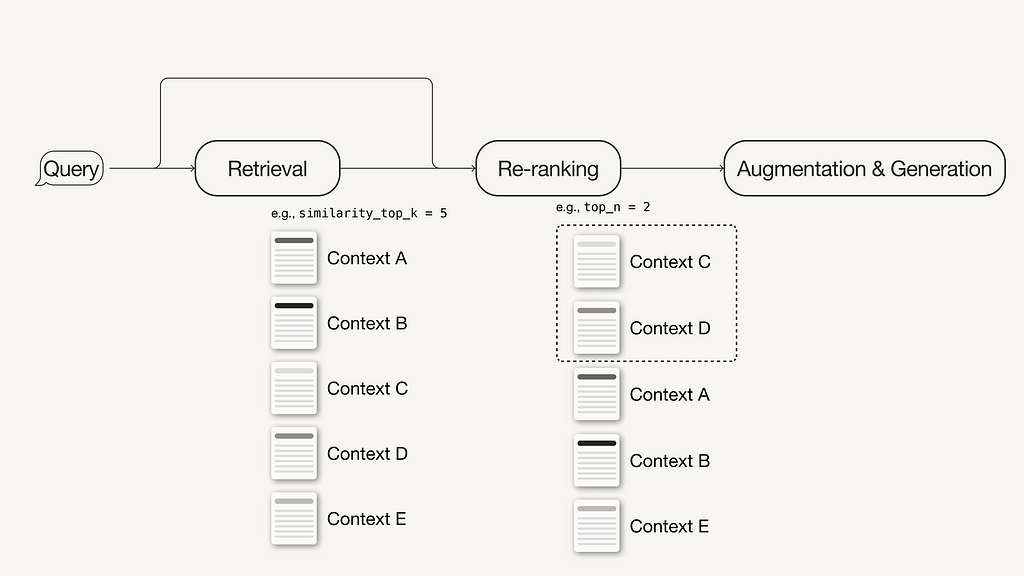
Adding a reranker to your advanced RAG pipeline only takes three simple steps:
# !pip install torch sentence-transformers
from llama_index.core.postprocessor import SentenceTransformerRerank
# Define reranker model
rerank = SentenceTransformerRerank(
top_n = 2,
model = "BAAI/bge-reranker-base"
)
...
# Add reranker to query engine
query_engine = index.as_query_engine(
similarity_top_k = 6,
...,
node_postprocessors = [rerank],
...,
)
There are many more different techniques within the advanced RAG paradigm. If you are interested in further implementations, I recommend the following two resources:
This article covered the concept of advanced RAG, which covers a set of techniques to address the limitations of the naive RAG paradigm. After an overview of advanced RAG techniques, which can be categorized into pre-retrieval, retrieval, and post-retrieval techniques, this article implemented a naive and advanced RAG pipeline using LlamaIndex for orchestration.
The RAG pipeline components were language models from OpenAI, a reranker model from BAAI hosted on Hugging Face, and a Weaviate vector database.
We implemented the following selection of techniques using LlamaIndex in Python:
You can find the Jupyter Notebooks containing the full end-to-end pipelines here:
Subscribe for free to get notified when I publish a new story.
Get an email whenever Leonie Monigatti publishes.
Find me on LinkedIn, Twitter, and Kaggle!
I am a Developer Advocate at Weaviate at the time of this writing.
[1] Gao, Y., Xiong, Y., Gao, X., Jia, K., Pan, J., Bi, Y., … & Wang, H. (2023). Retrieval-augmented generation for large language models: A survey. arXiv preprint arXiv:2312.10997.
If not otherwise stated, all images are created by the author.
Advanced Retrieval-Augmented Generation: From Theory to LlamaIndex Implementation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Advanced Retrieval-Augmented Generation: From Theory to LlamaIndex Implementation

Reinforcement learning (RL) stands as a pivotal element in the landscape of artificial intelligence, known for its unique method of teaching machines to make decisions through their own experiences within an environment. In this article, we’re going to take a deep dive into what makes RL tick. We’ll break down its core concepts, highlight the broad range of its applications, decode the math, and guide you through building it from scratch.
Index
· Introduction to Reinforcement Learning
∘ What is Reinforcement Learning?
∘ How does it work?
· The RL Framework
∘ States
∘ Actions
∘ Rewards
· The Concept of Episodes and Policy
∘ Episodes
∘ Policy
· Mathematical Formulation of the RL Problem
∘ Objective Function
∘ Return (Cumulative Reward)
∘ Discounting
· Next Steps
∘ Current Shortcomings
∘ Expanding Horizons: The Road Ahead

Reinforcement learning, or RL, is an area of artificial intelligence that’s all about teaching machines to make smart choices. Think of it as similar to training a dog. You give treats to encourage the behaviors you like, and over time, the dog — or in this case, a computer program — figures out which actions get the best results. But instead of yummy treats, we use numerical rewards, and the machine’s goal is to score as high as it can.
Now, your dog might not be a champ at board games, but RL can outsmart world champions. Take the time Google’s DeepMind introduced AlphaGo. This RL-powered software went head-to-head with Lee Sedol, a top player in the game Go, and won back in 2016. AlphaGo got better by playing loads of games against both human and computer opponents, learning and improving with each game.
But RL isn’t just for beating game champions. It’s also making waves in robotics, helping robots learn tasks that are tough to code directly, like grabbing and moving objects. And it’s behind the personalized recommendations you get on platforms like Netflix and Spotify, tweaking its suggestions to match what you like.
At the core of reinforcement learning (RL) is this dynamic between an agent (that’s you or the algorithm) and its environment. Picture this: you’re playing a video game. You’re the agent, the game’s world is the environment, and your mission is to rack up as many points as possible. Every moment in the game is a chance to make a move, and depending on what you do, the game throws back a new scenario and maybe some rewards (like points for snagging a coin or knocking out an enemy).
This give-and-take keeps going, with the agent (whether it’s you or the algorithm) figuring out which moves bring in the most rewards as time goes on. It’s all about trial and error, where the machine slowly but surely uncovers the best game plan, or policy, to hit its targets.
RL is a bit different from other ways of learning machines, like supervised learning, where a model learns from a set of data that already has the right answers, or unsupervised learning, which is all about spotting patterns in data without clear-cut instructions. With RL, there’s no cheat sheet. The agent learns purely through its adventures — making choices, seeing what happens, and learning from it.
This article is just the beginning of our “Reinforcement Learning 101” series. We’re going to break down the essentials of reinforcement learning, from the basic ideas to the intricate algorithms that power some of the most sophisticated AI out there. And here’s the fun part: you’ll get to try your hand at coding these concepts in Python, starting with our very first article. So, whether you’re a student, a developer, or just someone fascinated by AI, this series will give you the tools and knowledge to dive into the thrilling realm of reinforcement learning.
Let’s get started!
Let’s dive deeper into the heart of reinforcement learning, where everything revolves around the interaction between an agent and its environment. This relationship is all about a cycle of actions, states, and rewards, helping the agent learn the best way to act over time. Here’s a simple breakdown of these crucial elements:
A state represents the current situation or configuration of the environment.
The state is a snapshot of the environment at any given moment. It’s the backdrop against which decisions are made. In a video game, a state might show where all the players and objects are on the screen. States can range from something straightforward like a robot’s location on a grid, to something complex like the many factors that describe the stock market at any time.
Mathematically, we often write a state as s ∈ S, where S is the set of all possible states. States can be either discrete (like the spot of a character on a grid) or continuous (like the speed and position of a car).
To make this more clear, imagine a simple 5×5 grid. Here, states are where the agent is on the grid, marked by coordinates (x,y), with x being the row and y the column. In a 5×5 grid, there are 25 possible spots, from the top-left corner (0,0) to the bottom-right (4,4), covering everything in between.
Let’s say the agent’s mission is to navigate from a starting point to a goal, dodging obstacles along the way. Picture this grid: the start is a yellow block at the top-left, the goal is a light grey block at the bottom-right, and there are pink blocks as obstacles.
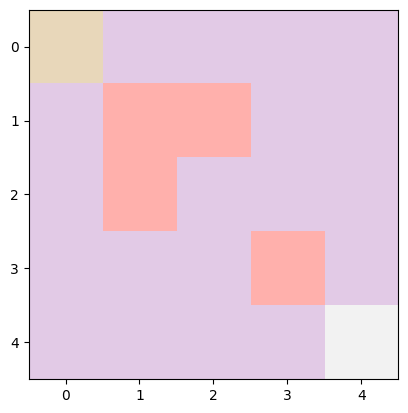
In a bit of code to set up this scenario, we’d define the grid’s size (5×5), the start point (0,0), the goal (4,4), and any obstacles. The agent’s current state starts at the beginning point, and we sprinkle in some obstacles for an extra challenge.
class GridWorld:
def __init__(self, width: int = 5, height: int = 5, start: tuple = (0, 0), goal: tuple = (4, 4), obstacles: list = None):
self.width = width
self.height = height
self.start = np.array(start)
self.goal = np.array(goal)
self.obstacles = [np.array(obstacle) for obstacle in obstacles] if obstacles else []
self.state = self.start
Here’s a peek at what that setup might look like in code. We set the grid to be 5×5, with the starting point at (0,0) and the goal at (4,4). We keep track of the agent’s current spot with self.state, starting at the start point. And we add obstacles to mix things up.
If this snippet of code seems a bit much right now, no worries! We’ll dive into a detailed example later on, making everything crystal clear.
Actions are the choices available to the agent that can change the state.
Actions are what an agent can do to change its current state. If we stick with the video game example, actions might include moving left or right, jumping, or doing something specific like shooting. The collection of all actions an agent can take at any point is known as the action space. This space can be discrete, meaning there’s a set number of actions, or continuous, where actions can vary within a range.
In math terms, we express an action as a ∈ A(s), where A represents the action space, and A(s) is the set of all possible actions in state s. Actions can be either discrete or continuous, just like states.
Going back to our simpler grid example, let’s define our possible moves:
action_effects = {'up': (-1, 0), 'down': (1, 0), 'left': (0, -1), 'right': (0, 1)}
Each action is represented by a tuple showing the change in position. So, to move down from the starting point (0,0) to (1,0), you’d adjust one row down. To move right, you go from (1,0) to (1,1) by changing one column. To transition from one state to the next, we simply add the action’s effect to the current position.
However, our grid world has boundaries and obstacles to consider, so we’ve got to make sure our moves don’t lead us out of bounds or into trouble. Here’s how we handle that:
# Check for boundaries and obstacles
if 0 <= next_state[0] < self.height and 0 <= next_state[1] < self.width and next_state not in self.obstacles:
self.state = next_state
This piece of code checks if the next move keeps us within the grid and avoids obstacles. If it does, the agent can proceed to that next spot.
So, actions are all about making moves and navigating the environment, considering what’s possible and what’s off-limits due to the layout and rules of our grid world.
Rewards are immediate feedback received from the environment following an action.
Rewards are like instant feedback that the agent gets from the environment after it makes a move. Think of them as points that show whether an action was beneficial or not. The agent’s main aim is to collect as many points as possible over time, which means it has to think about both the short-term gains and the long-term impacts of its actions. Just like we mentioned earlier with the dog training analogy when a dog does something good, we give it a treat; if not, there might be a mild telling-off. This idea is pretty much a staple in reinforcement learning.
Mathematically, we describe a reward that comes from making a move a in state s and moving to a new state s′ as R(s, a, s′). Rewards can be either positive (like a treat) or negative (more like a gentle scold), and they’re crucial for helping the agent learn the best actions to take.
In our grid world scenario, we want to give the agent a big thumbs up if it reaches its goal. And because we value efficiency, we’ll deduct points for every move it makes that doesn’t succeed. In code, we’d set up a reward system somewhat like this:
reward = 100 if (self.state == self.goal).all() else -1
This means the agent gets a whopping 100 points for landing on the goal but loses a point for every step that doesn’t get it there. It’s a simple way to encourage our agent to find the quickest route to its target.
Understanding episodes and policy is key to getting how agents learn and decide what to do in reinforcement learning (RL) environments. Let’s dive into these concepts:
An episode in reinforcement learning is a sequence of steps that starts in an initial state and ends when a terminal state is reached.
Think of an episode in reinforcement learning as a complete run of activity, starting from an initial point and ending when a specific goal is reached or a stopping condition is met. During an episode, the agent goes through a series of steps: it checks out the current situation (state), makes a move (action) based on its strategy (policy), and then gets feedback (reward) and the new situation (next state) from the environment. Episodes neatly package the agent’s experiences in scenarios where tasks have a clear start and finish.
In a video game, an episode might be tackling a single level, kicking off at the start of the level and wrapping up when the player either wins or runs out of lives.
In financial trading, an episode could be framed as a single trading day, starting when the market opens and ending at the close.
Episodes are useful because they let us measure how well different strategies (policies) work over a set period and help in learn from a full experience. This setup gives the agent chances to restart, apply what it’s learned, and experiment with new tactics under similar conditions.
Mathematically, you can visualize an episode as a series of moments:

where:
This sequence helps in tracking the flow of actions, states, and rewards throughout an episode, providing a framework for learning and improving strategies.
A policy is the strategy that an RL agent employs to decide which actions to take in various states.
In the world of reinforcement learning (RL), a policy is essentially the game plan an agent follows to decide its moves in different situations. It’s like a guidebook that maps out which actions to take when faced with various scenarios. Policies can come in two flavors: deterministic and stochastic.
Deterministic Policy
A deterministic policy is straightforward: for any specific situation, it tells the agent exactly what to do. If you find yourself in a state s, the policy has a predefined action a ready to go. This kind of policy always picks the same action for a given state, making it predictable. You can think of a deterministic policy as a direct function that links states to their corresponding actions:

where a is the action chosen when the agent is in state s.
Stochastic Policy
On the flip side, a stochastic policy adds a bit of unpredictability to the mix. Instead of a single action, it gives a set of probabilities for choosing among available actions in a given state. This randomness is crucial for exploring the environment, especially when the agent is still figuring out which actions work best. A stochastic policy is often expressed as a probability distribution over actions given a state s, symbolized as π(a ∣ s), indicating the likelihood of choosing action a when in state s:

where P denotes the probability.
The endgame of reinforcement learning is to uncover the optimal policy, one that maximizes the total expected rewards over time. Finding this balance between exploring new actions and exploiting known lucrative ones is key. The idea of an “optimal policy” ties closely to the value function concept, which gauges the anticipated rewards (or returns) from each state or action-state pairing, based on the policy in play. This journey of exploration and exploitation helps the agent learn the best paths to take, aiming for the highest cumulative reward.
The way reinforcement learning (RL) problems are set up mathematically is key to understanding how agents learn to make smart decisions that maximize their rewards over time. This setup involves a few main ideas: the objective function, return (or cumulative reward), discounting, and the overall goal of optimization. Let’s dig into these concepts:
At the core of RL is the objective function, which is the target that the agent is trying to hit by interacting with the environment. Simply put, the agent wants to collect as many rewards as it can. We measure this goal using the expected return, which is the total of all rewards the agent thinks it can get, starting from a certain point and following a specific game plan or policy.
“Return” is the term used for the total rewards that an agent picks up, whether that’s in one go (a single episode) or over a longer period. You can think of it as the agent’s score, where every move it makes either earns or loses points based on how well it turns out. If we’re not thinking about discounting for a moment, the return is just the sum of all rewards from each step t until the episode ends:

Here, Rt represents the reward obtained at time t, and T marks the episode’s conclusion.
In RL, not every reward is seen as equally valuable. There’s a preference for rewards received sooner rather than later, and this is where discounting comes into play. Discounting reduces the value of future rewards with a discount factor γ, which is a number between 0 and 1. The discounted return formula looks like this:
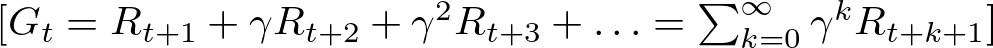
This approach keeps the agent’s score from blowing up to infinity, especially when we’re looking at endless scenarios. It also encourages the agent to prioritize actions that deliver rewards more quickly, balancing the pursuit of immediate versus future gains.
Now, let’s take the grid example we talked about earlier, and write a code to implement an agent navigating through the environment and reaching its goal. Let’s construct a straightforward grid world environment, outline a navigation policy for our agent, and kick off a simulation to see everything in action.
Let’s first show all the code and then let’s break it down.
import numpy as np
import matplotlib.pyplot as plt
import logging
logging.basicConfig(level=logging.INFO)
class GridWorld:
"""
GridWorld environment for navigation.
Args:
- width: Width of the grid
- height: Height of the grid
- start: Start position of the agent
- goal: Goal position of the agent
- obstacles: List of obstacles in the grid
Methods:
- reset: Reset the environment to the start state
- is_valid_state: Check if the given state is valid
- step: Take a step in the environment
"""
def __init__(self, width: int = 5, height: int = 5, start: tuple = (0, 0), goal: tuple = (4, 4), obstacles: list = None):
self.width = width
self.height = height
self.start = np.array(start)
self.goal = np.array(goal)
self.obstacles = [np.array(obstacle) for obstacle in obstacles] if obstacles else []
self.state = self.start
self.actions = {'up': np.array([-1, 0]), 'down': np.array([1, 0]), 'left': np.array([0, -1]), 'right': np.array([0, 1])}
def reset(self):
"""
Reset the environment to the start state
Returns:
- Start state of the environment
"""
self.state = self.start
return self.state
def is_valid_state(self, state):
"""
Check if the given state is valid
Args:
- state: State to be checked
Returns:
- True if the state is valid, False otherwise
"""
return 0 <= state[0] < self.height and 0 <= state[1] < self.width and all((state != obstacle).any() for obstacle in self.obstacles)
def step(self, action: str):
"""
Take a step in the environment
Args:
- action: Action to be taken
Returns:
- Next state, reward, done
"""
next_state = self.state + self.actions[action]
if self.is_valid_state(next_state):
self.state = next_state
reward = 100 if (self.state == self.goal).all() else -1
done = (self.state == self.goal).all()
return self.state, reward, done
def navigation_policy(state: np.array, goal: np.array, obstacles: list):
"""
Policy for navigating the agent in the grid world environment
Args:
- state: Current state of the agent
- goal: Goal state of the agent
- obstacles: List of obstacles in the environment
Returns:
- Action to be taken by the agent
"""
actions = ['up', 'down', 'left', 'right']
valid_actions = {}
for action in actions:
next_state = state + env.actions[action]
if env.is_valid_state(next_state):
valid_actions[action] = np.sum(np.abs(next_state - goal))
return min(valid_actions, key=valid_actions.get) if valid_actions else None
def run_simulation_with_policy(env: GridWorld, policy):
"""
Run the simulation with the given policy
Args:
- env: GridWorld environment
- policy: Policy to be used for navigation
"""
state = env.reset()
done = False
logging.info(f"Start State: {state}, Goal: {env.goal}, Obstacles: {env.obstacles}")
while not done:
# Visualization
grid = np.zeros((env.height, env.width))
grid[tuple(state)] = 1 # current state
grid[tuple(env.goal)] = 2 # goal
for obstacle in env.obstacles:
grid[tuple(obstacle)] = -1 # obstacles
plt.imshow(grid, cmap='Pastel1')
plt.show()
action = policy(state, env.goal, env.obstacles)
if action is None:
logging.info("No valid actions available, agent is stuck.")
break
next_state, reward, done = env.step(action)
logging.info(f"State: {state} -> Action: {action} -> Next State: {next_state}, Reward: {reward}")
state = next_state
if done:
logging.info("Goal reached!")
# Define obstacles in the environment
obstacles = [(1, 1), (1, 2), (2, 1), (3, 3)]
# Create the environment with obstacles
env = GridWorld(obstacles=obstacles)
# Run the simulation
run_simulation_with_policy(env, navigation_policy)
Link to full code:
GridWorld Class
class GridWorld:
def __init__(self, width: int = 5, height: int = 5, start: tuple = (0, 0), goal: tuple = (4, 4), obstacles: list = None):
self.width = width
self.height = height
self.start = np.array(start)
self.goal = np.array(goal)
self.obstacles = [np.array(obstacle) for obstacle in obstacles] if obstacles else []
self.state = self.start
self.actions = {'up': np.array([-1, 0]), 'down': np.array([1, 0]), 'left': np.array([0, -1]), 'right': np.array([0, 1])}
This class initializes a grid environment with a specified width and height, a start position for the agent, a goal position to reach, and a list of obstacles. Note that obstacles are a list of tuples, where each tuple represents the position of each obstacle.
Here, self.actions defines possible movements (up, down, left, right) as vectors that will modify the agent’s position.
def reset(self):
self.state = self.start
return self.state
reset() method sets the agent’s state back to the start position. This is useful when we want to train the agent several times, after each completion of the reach of a certain status, the agent will start back from the beginning.
def is_valid_state(self, state):
return 0 <= state[0] < self.height and 0 <= state[1] < self.width and all((state != obstacle).any() for obstacle in self.obstacles)
is_valid_state(state) checks if a given state is within the grid boundaries and not an obstacle.
def step(self, action: str):
next_state = self.state + self.actions[action]
if self.is_valid_state(next_state):
self.state = next_state
reward = 100 if (self.state == self.goal).all() else -1
done = (self.state == self.goal).all()
return self.state, reward, done
step(action: str) moves the agent according to the action if it’s valid, updates the state, calculates the reward, and checks if the goal is reached.
Navigation Policy Function
def navigation_policy(state: np.array, goal: np.array, obstacles: list):
actions = ['up', 'down', 'left', 'right']
valid_actions = {}
for action in actions:
next_state = state + env.actions[action]
if env.is_valid_state(next_state):
valid_actions[action] = np.sum(np.abs(next_state - goal))
return min(valid_actions, key=valid_actions.get) if valid_actions else None
Defines a simple policy to decide the next action based on minimizing the distance to the goal while considering valid actions only. Indeed, for every valid action we calculate the distance between the new state and the goal, then we select the action that minimizes the distance. Keep in mind, that the function to calculate the distance is crucial for a performant RL agent. In this case, we are using a Manhattan distance calculation, but this may not be the best choice for different and more complex scenarios.
Simulation Function
def run_simulation_with_policy(env: GridWorld, policy):
state = env.reset()
done = False
logging.info(f"Start State: {state}, Goal: {env.goal}, Obstacles: {env.obstacles}")
while not done:
# Visualization
grid = np.zeros((env.height, env.width))
grid[tuple(state)] = 1 # current state
grid[tuple(env.goal)] = 2 # goal
for obstacle in env.obstacles:
grid[tuple(obstacle)] = -1 # obstacles
plt.imshow(grid, cmap='Pastel1')
plt.show()
action = policy(state, env.goal, env.obstacles)
if action is None:
logging.info("No valid actions available, agent is stuck.")
break
next_state, reward, done = env.step(action)
logging.info(f"State: {state} -> Action: {action} -> Next State: {next_state}, Reward: {reward}")
state = next_state
if done:
logging.info("Goal reached!")
run_simulation_with_policy(env: GridWorld, policy) resets the environment and iteratively applies the navigation policy to move the agent towards the goal. It visualizes the grid and the agent’s progress at each step.
The simulation runs until the goal is reached or no valid actions are available (the agent is stuck).
Running the Simulation
# Define obstacles in the environment
obstacles = [(1, 1), (1, 2), (2, 1), (3, 3)]
# Create the environment with obstacles
env = GridWorld(obstacles=obstacles)
# Run the simulation
run_simulation_with_policy(env, navigation_policy)
The simulation is run using run_simulation_with_policy, applying the defined navigation policy to guide the agent.

By developing this RL environment and simulation, you get a firsthand look at the basics of agent navigation and decision-making, foundational concepts in the field of reinforcement learning.
As we delve deeper into the world of reinforcement learning (RL), it’s important to take stock of where we currently stand. Here’s a rundown of what our current approach lacks and our plans for bridging these gaps:
Static Environment
Our simulations run in a fixed grid world, with unchanging obstacles and goals. This setup doesn’t challenge the agent with new or evolving obstacles, limiting its need to adapt or strategize beyond the basics.
Basic Navigation Policy
The policy we’ve implemented is quite basic, focusing solely on obstacle avoidance and goal achievement. It lacks the depth required for more complex decision-making or learning from past interactions with the environment.
No Learning Mechanism
As it stands, our agent doesn’t learn from its experiences. It reacts to immediate rewards without improving its approach based on past actions, missing out on the essence of RL: learning and improving over time.
Absence of MDP Framework
Our current model does not explicitly utilize the Markov Decision Process (MDP) framework. MDPs are crucial for understanding the dynamics of state transitions, actions, and rewards, and are foundational for advanced learning algorithms like Q-learning.
Recognizing these limitations is the first step toward enhancing our RL exploration. Here’s what we plan to tackle in the next article:
Dynamic Environment
We’ll upgrade our grid world to introduce elements that change over time, such as moving obstacles or changing rewards. This will compel the agent to continuously adapt its strategies, offering a richer, more complex learning experience.
Implementing Q-learning
To give our agent the ability to learn and evolve, we’ll introduce Q-learning. This algorithm is a game-changer, enabling the agent to accumulate knowledge and refine its strategies based on the outcomes of past actions.
Exploring MDPs
Diving into the Markov Decision Process will provide a solid theoretical foundation for our simulations. Understanding MDPs is key to grasping decision-making in uncertain environments, evaluating and improving policies, and how algorithms like Q-learning fit into this framework.
Complex Algorithms and Strategies
With the groundwork laid by Q-learning and MDPs, we’ll explore more sophisticated algorithms and strategies. This advancement will not only elevate our agent’s intelligence but also its proficiency in navigating the intricacies of a dynamic and challenging grid world.
By addressing these areas, we aim to unlock new levels of complexity and learning in our reinforcement learning journey. The next steps promise to transform our simple agent into one capable of making informed decisions, adapting to changing environments, and continuously learning from its experiences.
Wrapping up our initial dive into the core concepts of reinforcement learning (RL) within the confines of a simple grid world, it’s clear we’ve only scratched the surface of what’s possible. This first article has set the stage, showcasing both the promise and the current constraints of our approach. The simplicity of our static setup and the basic nature of our navigation tactics have spotlighted key areas ready for advancement.
You made it to the end. Congrats! I hope you enjoyed this article. If so consider leaving a clap and following me, as I will regularly post similar articles. As with every beginning of a new series, this article may not be perfect, and with your input, it can highly improve. So, let me know what you think about it, what you would like to see more, and what less.
Reinforcement Learning 101: Building a RL Agent was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Reinforcement Learning 101: Building a RL Agent
Go Here to Read this Fast! Reinforcement Learning 101: Building a RL Agent