Building Blocks of Time: The Mathematical Foundation and Python Implementation of RNNs

Is being able to build and train machine learning models from popular libraries sufficient for machine learning users? Probably not for too long. With tools like AutoAI on the rise, it is likely that a lot of the very traditional machine learning skills like building model architectures with common libraries like Pytorch will be less important.

What is likely to persist is the demand for skilled users with a deep understanding of the underlying principles of ML, particularly in problems that require novel challenges, customisation, optimisation. To be more innovative and novel, it is important to have a deep understanding of the mathematical foundations of these algorithms. In this article, we’ll look at the mathematical description of one such important model, Recurrent Neural Network (RNN).

Time series data (or any sequential data like language) has a temporal dependencies and is widespread across various sectors ranging from weather prediction to medical applications. RNN is a powerful tool for capturing sequential patterns in such data. In this article, we’ll delve into the mathematical foundations of RNNs and implement these equations from scratch using python.

Understanding RNNs: The Mathematical Description

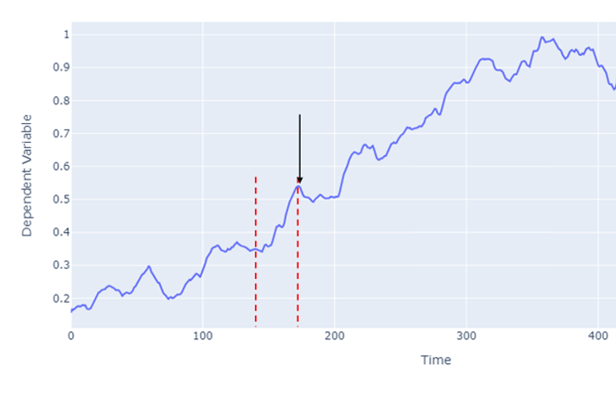
An important element of sequential data is the temporal dependence where the past values determine the current and future values (just like the predetermined world we live in but let’s not get philosophical and stick to RNN models). Time series forecasting utilises this nature of sequential data and focuses on the prediction of the next value given previous n values. Depending on the model, this includes either mapping or regression of the past values.

Consider the point indicated with the black arrow, y and the points before y (between the red dashed line) denoting as X = {x1 , x2 , ….xt …..xT} where T is the total number of time steps. The RNN processes the input sequence (X) by placing each input through a hidden state (or sometimes refered to as memory state) and outputs y. These hidden states allow the model to capture and remember patterns from earlier points in the sequence.

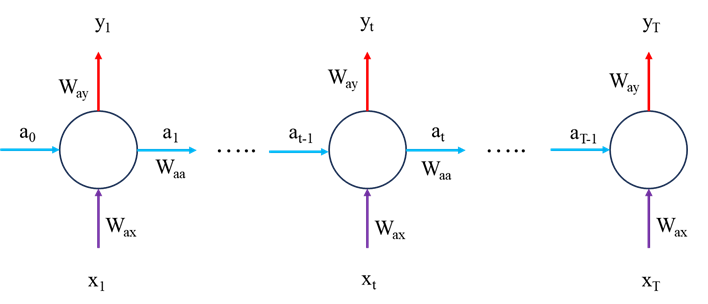
Now let’s look at the mathematical operations within the RNN model, first lets consider the forward pass, we’ll worry about the model optimisation later.

Forward Pass

The forward pass is fairly straightforward and is as follows:

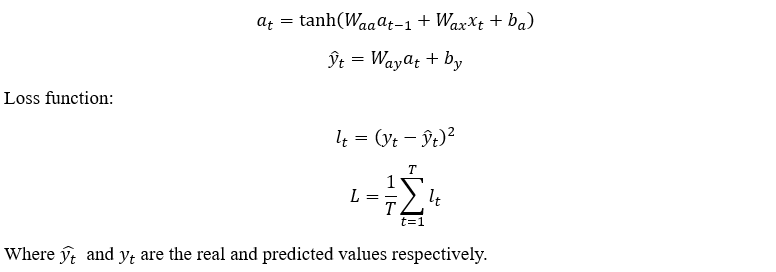
Backpropagation Through Time

In machine learning, the optimisation (variable updates) are done using the gradient descent method:

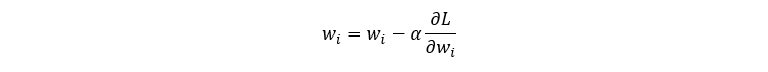
Therefore, all parameters that need updating during training will require their partial derivatives. Here we’ll derive the partial derivative of the loss function with respect to each variable included in the forward pass equations:

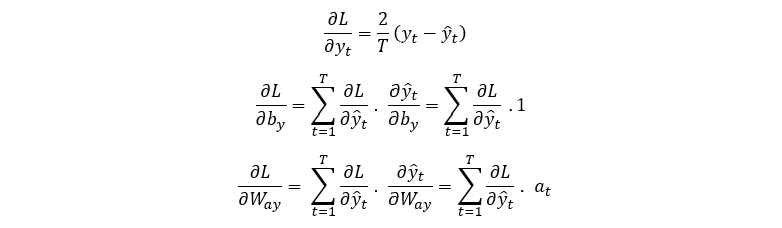
By noting the forward pass equations and network schematic in Figure 2, we can see that at time T, L only depends on a_T via y_T i.e.

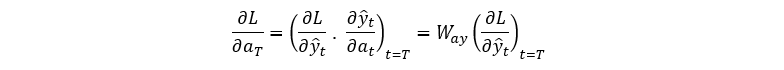
However, for t < T, L depends on a_T via y_T and a_(T+1) so let’s use the chain rule for both:

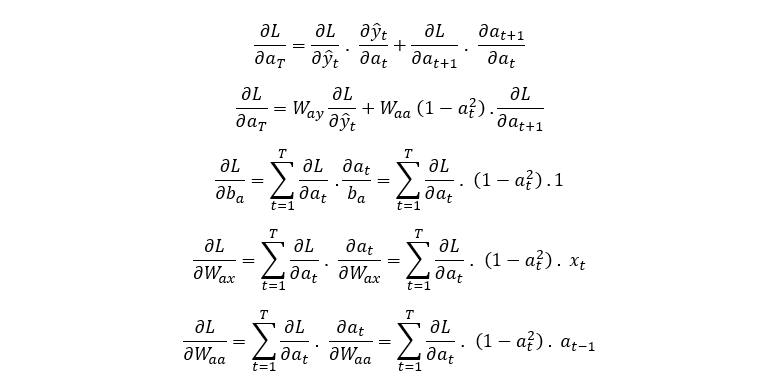
Now we have the equations for the gradient of the loss function with respect all parameters present in the forward pass equation. This algorithm is called Backpropagation Through Time. It is important to clarify that for a time series data, usually only the last value contribute to the Loss function i.e. all other outputs are ignored and their contribution to the loss function set to 0. The mathematical description is the same as that presented. Now Let’s code these equations in python and apply it to an example dataset.

The Coding Implementation

Before we can implement the equations above, we’ll need to import the necessary dataset, preprocess and ready for the model training. All of this work is very standard in any time series analysis.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.graph_objs as go
from plotly.offline import iplot
import yfinance as yf
import datetime as dt
import math

#### Data Processing
start_date = dt.datetime(2020,4,1)
end_date = dt.datetime(2023,4,1)

#loading from yahoo finance
data = yf.download("GOOGL",start_date, end_date)

pd.set_option('display.max_rows', 4)
pd.set_option('display.max_columns',5)
display(data)


# #Splitting the dataset
training_data_len = math.ceil(len(data) * .8)
train_data = data[:training_data_len].iloc[:,:1]
test_data = data[training_data_len:].iloc[:,:1]

dataset_train = train_data.Open.values
# Reshaping 1D to 2D array
dataset_train = np.reshape(dataset_train, (-1,1))
dataset_train.shape
scaler = MinMaxScaler(feature_range=(0,1))
# scaling dataset
scaled_train = scaler.fit_transform(dataset_train)

dataset_test = test_data.Open.values
dataset_test = np.reshape(dataset_test, (-1,1))
scaled_test = scaler.fit_transform(dataset_test)


X_train = []
y_train = []
for i in range(50, len(scaled_train)):
    X_train.append(scaled_train[i-50:i, 0])
    y_train.append(scaled_train[i, 0])

X_test = []
y_test = []
for i in range(50, len(scaled_test)):
    X_test.append(scaled_test[i-50:i, 0])
    y_test.append(scaled_test[i, 0])

# The data is converted to Numpy array
X_train, y_train = np.array(X_train), np.array(y_train)

#Reshaping
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1],1))
y_train = np.reshape(y_train, (y_train.shape[0],1))
print("X_train :",X_train.shape,"y_train :",y_train.shape)

# The data is converted to numpy array
X_test, y_test = np.array(X_test), np.array(y_test)

#Reshaping
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1],1))
y_test = np.reshape(y_test, (y_test.shape[0],1))

The model
Now we implement the mathematical equations. it is definitely worth reading through the code, noting the dimensions of all variables and respective derivates to give yourself a better understanding of these equations.

class SimpleRNN:
    def __init__(self,input_dim,output_dim, hidden_dim):
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.hidden_dim = hidden_dim
        self.Waa = np.random.randn(hidden_dim, hidden_dim) * 0.01 # we initialise as non-zero to help with training later
        self.Wax = np.random.randn(hidden_dim, input_dim) * 0.01
        self.Way = np.random.randn(output_dim, hidden_dim) * 0.01
        self.ba = np.zeros((hidden_dim, 1))
        self.by = 0 # a single value shared over all outputs #np.zeros((hidden_dim, 1))

    def FeedForward(self, x):
        # let's calculate the hidden states
        a = [np.zeros((self.hidden_dim,1))]
        y = []
        for ii in range(len(x)):

            a_next = np.tanh(np.dot(self.Waa, a[ii])+np.dot(self.Wax,x[ii].reshape(-1,1))+self.ba)
            a.append(a_next)
            y_local = np.dot(self.Way,a_next)+self.by
            y.append(np.dot(self.Way,a_next)+self.by)

        # remove the first a and y values used for initialisation
        #a = a[1:]
        return y, a
    
    def ComputeLossFunction(self, y_pred, y_actual):
        # for a normal many to many model:
        #loss = np.sum((y_pred - y_actual) ** 2)
        # in our case, we are only using the last value so we expect scalar values here rather than a vector
        loss = (y_pred[-1] - y_actual) ** 2
        return loss
    
    def ComputeGradients(self, a, x, y_pred, y_actual):
        # Backpropagation through time
        dLdy = []
        dLdby = np.zeros((self.output_dim, 1))
        dLdWay = np.random.randn(self.output_dim, self.hidden_dim)/5.0
        dLdWax = np.random.randn(self.hidden_dim, self.input_dim)/5.0
        dLdWaa = np.zeros((self.hidden_dim, self.hidden_dim))
        dLda = np.zeros_like(a)
        dLdba = np.zeros((self.hidden_dim, 1))
        
        for t in range(self.hidden_dim-1, 0, -1):
            if t == self.hidden_dim-1:
                dldy = 2*(y_pred[t] - y_actual)
            else:
                dldy = 0
            dLdy.append(dldy)
            #dLdby.append(dldy)
            dLdby += dldy
            #print(dldy.shape)
            dLdWay += np.dot(np.array(dldy).reshape(-1,1), a[t].T)
            
            # Calculate gradient of loss with respect to a[t]
            if t == self.hidden_dim-1:
                dlda_t= np.dot(self.Way.T, np.array(dldy).reshape(-1,1))

            else:
                dlda_t = np.dot(self.Way.T, np.array(dldy).reshape(-1,1)) + np.dot(self.Waa, dLda[t+1]) * (1 - a[t]**2)
            dLda[t] = dlda_t
            #print(dlda_t.shape)
            
            rec_term = (1-a[t]*a[t])
             
            dLdWax += np.dot(dlda_t, x[t].reshape(-1,1))*rec_term
            dLdWaa += np.dot(dlda_t, a[t-1].T)*rec_term
            dLdba += dlda_t*rec_term
        
        return dLdy[::-1], dLdby[::-1], dLdWay, dLdWax, dLdWaa, dLdba
    
    def UpdateParameters(self,dLdby, dLdWay, dLdWax, dLdWaa, dLdba,learning_rate):
        self.Waa -= learning_rate * dLdWaa
        self.Wax -= learning_rate * dLdWax
        self.Way -= learning_rate * dLdWay
        self.ba -= learning_rate * dLdba
        self.by -= learning_rate * dLdby    
    
    def predict(self, x, n, a_training):
        # let's calculate the hidden states
        a_future = a_training
        y_predict = []

        # Predict the next n terms
        for ii in range(n):
            a_next = np.tanh(np.dot(self.Waa, a_future[-1]) + np.dot(self.Wax, x[ii]) + self.ba)
            a.append(a_next)
            y_predict.append(np.dot(self.Way, a_next) + self.by)

        return y_predict

Training and Testing the model

input_dim = 1
output_dim = 1
hidden_dim = 50

learning_rate = 1e-3

# Initialize The RNN model
rnn_model = SimpleRNN(input_dim, output_dim, hidden_dim)

# train the model for 200 epochs

for epoch in range(200):
    for ii in range(len(X_train)):
        y_pred, a = rnn_model.FeedForward(X_train[ii])
        loss = rnn_model.ComputeLossFunction(y_pred, y_train[ii])
        dLdy, dLdby, dLdWay, dLdWax, dLdWaa, dLdba = rnn_model.ComputeGradients(a, X_train[ii], y_pred, y_train[ii])
        rnn_model.UpdateParameters(dLdby, dLdWay, dLdWax, dLdWaa, dLdba, learning_rate)
        print(f'Loss: {loss}')


y_test_predicted = []
for jj in range(len(X_test)):
    forecasted_values, _ = rnn_model.FeedForward(X_test[jj])
    y_test_predicted.append(forecasted_values[-1])

y_test_predicted_flat = np.array([val[0, 0] for val in y_test_predicted])
trace1 = go.Scatter(y = y_test.ravel(), mode ="lines", name = "original data")
trace2 = go.Scatter(y=y_test_predicted_flat, mode = "lines", name = "RNN output")
layout = go.Layout(title='Testing data Fit', xaxis=dict(title='X-Axis'), yaxis=dict(title='Dependent Variable'))
figure = go.Figure(data = [trace1,trace2], layout = layout)

iplot(figure)

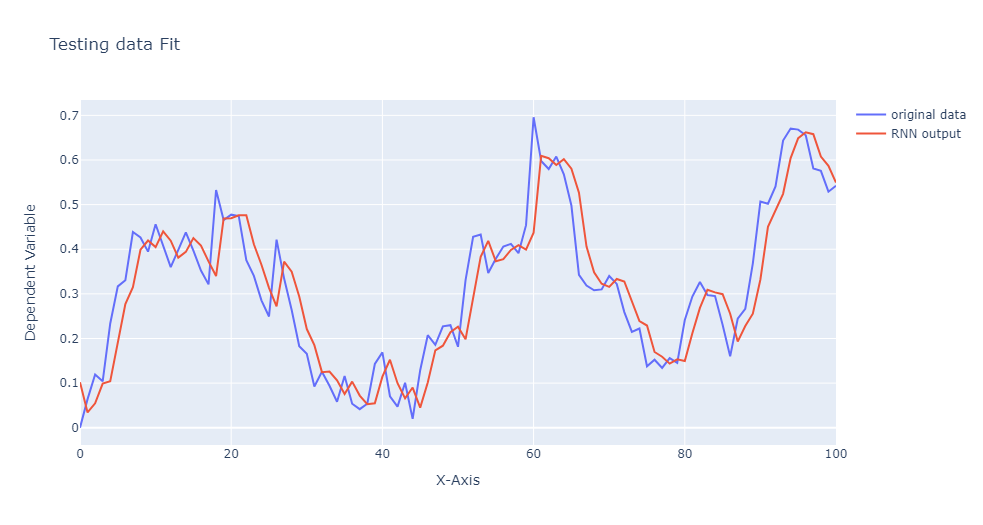
That brings us to the end of this demonstration but hopefully only the start of your reading into these powerful models. You might find it helpful to test your understanding by experimenting with a different activation function in the forward pass. Or read further into sequential models like LSTM and transformers which are formidable tools, especially in language-related tasks. Exploring these models can deepen your understanding of more sophisticated mechanisms for handling temporal dependencies. Finally, thank you for taking the time to read this article, I hope you found it useful in your understanding of RNN or their mathematical background.

Unless otherwise noted, all images are by the author

Building Blocks of Time: The Mathematical Foundation and Python Implementation of RNNs was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.