Beyond Attention: How Advanced Positional Embedding Methods Improve upon the Original Transformers

Beyond Attention: How Advanced Positional Embedding Methods Improve upon the Original Approach in Transformer Architecture

From Sinusoidal to RoPE and ALiBi: How advanced positional encodings overcome limitations in Transformers

Authors: Elahe Aghapour, Salar Rahili

Introduction:

The exponential progress of models built in recent years is deeply connected with the advent of the Transformer architecture. Previously, AI scientists had to select architectures for each task at hand, and then optimize the hyper-parameters to get the best performance out of it. Another challenge limiting their potential was the difficulty in handling long-range dependencies of the data, surfacing the issues of vanishing gradients, loss of context over long sequences, and the inability to capture global context due to locality constraints. Additionally, the lack of scalability and parallelization in traditional models slowed training on large datasets, holding back the progress in the field.

The Transformer architecture revolutionized the field by addressing these issues through its self-attention mechanism. It enabled models to capture relationships over long sequences and efficiently understand global context, all while being highly parallelizable and adaptable across various modalities, such as text, images, and more. In the self-attention mechanism, for each token, its query is compared against the keys of all other tokens to compute similarity scores. These similarities are then used to weigh the value vectors, which ultimately decide where the current token should attend to. Self-attention treats all tokens as equally important regardless of their order, losing critical information about the sequence in which tokens appear, and in other words, it sees the input data as a set with no order. Now we need a mechanism to enforce some notion of order on the data, as natural language and many other types of data are inherently sequential and position-sensitive. This is where positional embeddings come into play. Positional embeddings encode the position of each token in the sequence, enabling the model to maintain awareness of the sequence’s structure. Various methods for encoding positional information have been explored, and we will cover them in this blog post.

Attention Mechanism:

Let S = {wi} for i =1,…,N be a sequence of N input tokens where wi represents the i-th token. Hence, the corresponding token embedding of S can be denoted as E = {xi} for i =1,…,N where xi is the d-dimensional token embedding vector for token wi. The self-attention mechanism incorporates position embedding into token embeddings and generates the query, key, and value representations as:

Then, the attention weights is computed based on the similarity between query and key vectors:

The attention weights determine how important token n is for token m. In the other words, how much attention token m should pay to token n. The output for token m is computed as a weighted sum of the value vectors:

Therefore, the attention mechanism token m to gather information from other tokens in the sequence.

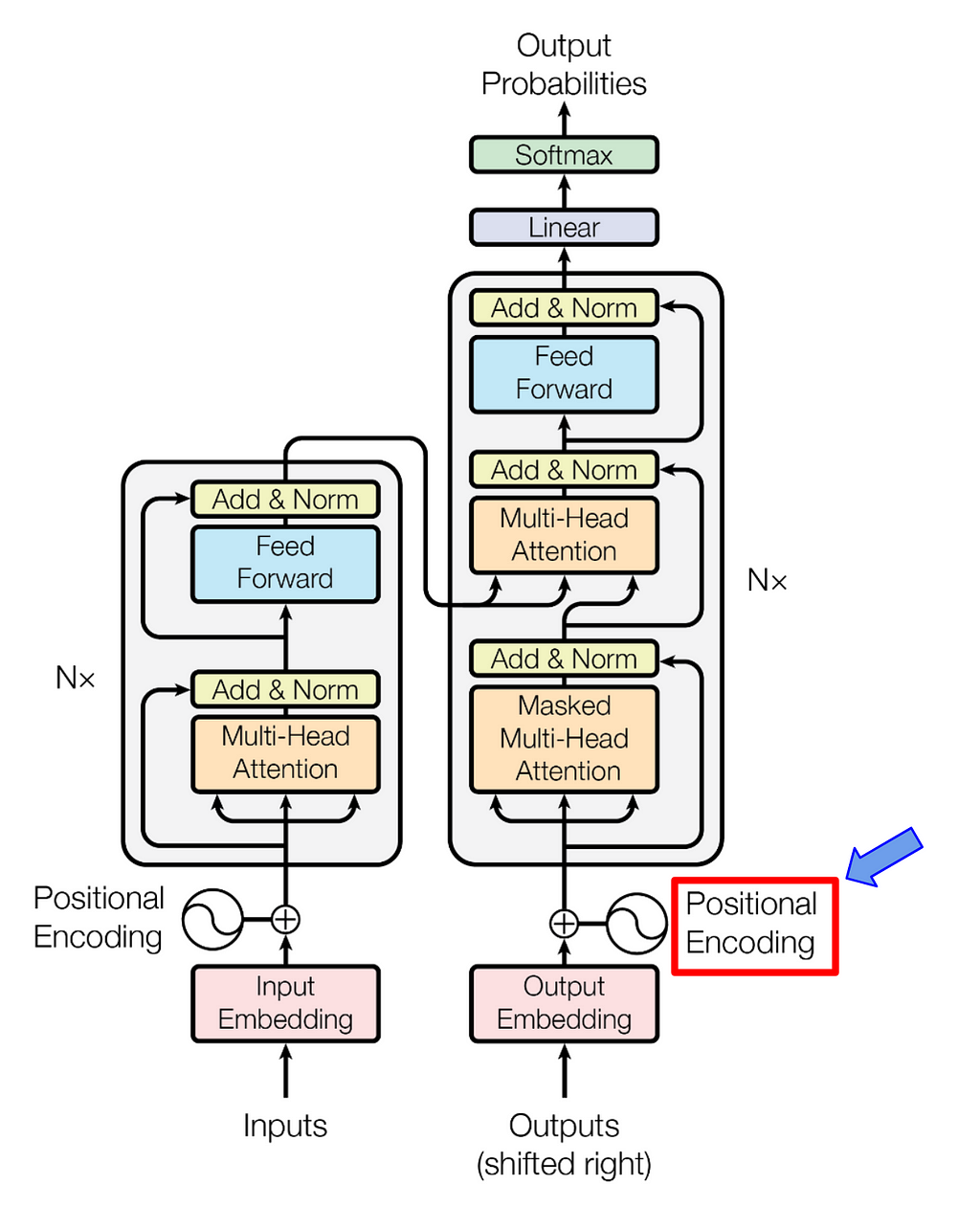
1. Absolute Position Embedding:

A typical choice for the equation (1) is to have:

Where pi is a d-dimensional vector, representing the absolute position of token xi. Sinusoidal positional encoding and learned positional encoding are two alternatives to generate pi.

1.a Sinusoidal Positional Encoding

Sinusoidal positional encoding was introduced in the “Attention is all you need” paper where transformer architecture was proposed. Sinusoidal Positional Encoding provides a unique position representation for each token in the input sequence. It is based on sine and cosine functions with different frequencies as:

Where pos is the position of the token in the sequence, d is the position embedding dimension, and i is the dimension index (0<=i<d).

The use of sine and cosine functions in sinusoidal positional encoding has a deep relationship with the Fourier transform. By using a range of different frequencies to encode positions, the Transformer creates a representation similar to a Fourier transform where:

• High-frequency components (lower i) enable the model to capture local positional information. This is useful for understanding relationships between neighbor tokens in a sequence, such as word pairs.
• Low-frequency components (higher i) capture more global patterns over the entire sequence. This helps the model to focus on broader relationships between tokens that may be far apart, such as dependencies between words in two different sentences.

This helps the model understand the relative positions of tokens by comparing their positional encodings. Sinusoidal positional encoding needs no additional training parameters while generalizing to larger sequence lengths at inference time. However, its expressiveness is limited.

1.b Learned Positional Encoding

Learned positional encoding was introduced in the “Attention is all you need” paper and it was applied in the BERT and GPT models as an alternative to Sinusoidal positional encoding. In learned positional encoding, each position in the sequence (e.g. first token, second token, etc) is assigned an embedding vector. These position embeddings are learned along with other transformer parameters during training. For example, if the model has a context length of 512 with a token embedding of size 768 (i.e. d=768), a learnable tensor of size 512*768 will be added to the other trainable parameters. This means the model gradually learns the best way to encode positional information for the specific task, such as text classification or translation.

Learned positional embedding is more expressive than sinusoidal one as the model can learn a position embedding, effective for its specific task. However, they introduce more trainable parameters which increases the model size and its computational cost.

2. Relative Positional Embeddings

Both sinusoidal and learned position encodings focused on the absolute position of the token. However, the attention mechanism works by computing how important other tokens are for each specific token in the sequence. Hence, this process depends on the relative position of the tokens (how far apart they are from each other), rather than the absolute position of the tokens. To address the limitations of absolute position embedding, relative position encoding was introduced.

RelativePosEmb doesn’t add position information to token embeddings. Instead, it modifies the way key and value are computed at every layer as:

Here, r = clip(m-n, Rmin, Rmax) represents the relative distance between position m and n. The maximum relative position is clipped, assuming that precise relative position is not useful beyond a certain distance. Clipping the maximum distance enables the model to extrapolate at inference time, i.e. to generalize to sequence length not seen during training. However, this approach may miss some useful information from the absolute position of the token (like the position of the first token).

You may notice that fq lacks position embedding. That’s because we are encoding the relative position. In the attention formula, the query and key values are used to compute attention weights as equation (2) therefore we only need either the query or the key to include the relative position embedding.

This encoding has been used in many models as Transformer-XL and T5. There are different alternatives in applying relative positional encoding that you can find in papers [7] and [8] .

3. Rotary Positional Embedding (RoPE)

Unlike previous methods, RoPE rotates the vectors in a multi-dimensional space based on the position of tokens. Instead of adding position information to token embeddings, it modifies the way attention weights are computed at every layer as:

They proposed a generalized rotation matrix to any even embedding dimensionality d as:

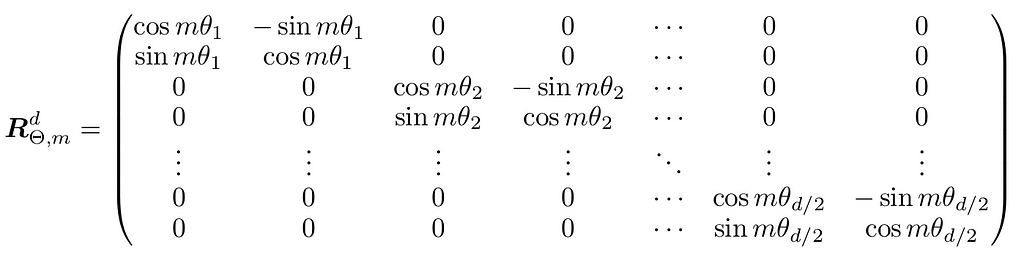
Where θi is pre-defined:

Applying RoPE to attention weight yields to:

Note that RoPE formulation doesn’t add position information to the values in the attention module. The output of the attention module is a weighted sum of the value vector and since position information isn’t added to values, the outputs of each transformer layer don’t have explicit position details.

Popular models such as LLaMA and GPT-NeoX are using RoPE.

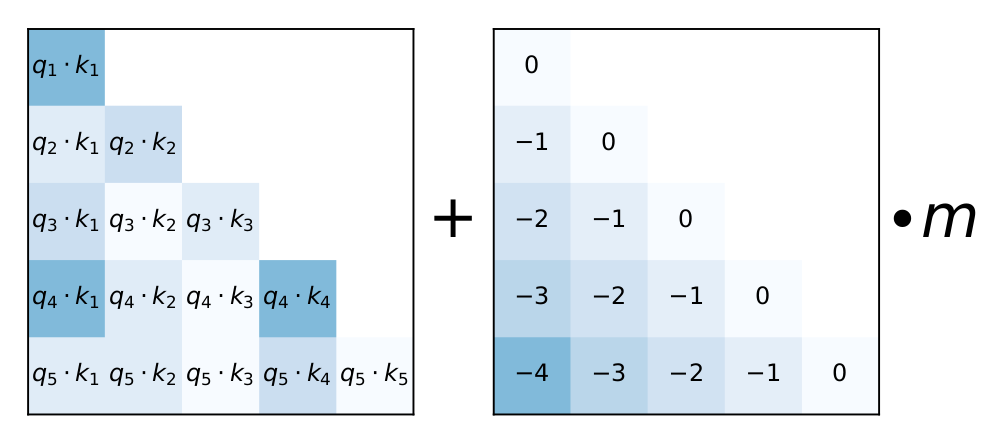
4. Attention with Linear Biases (ALiBi)

ALiBi also does not add positional encodings to word embeddings; instead, it adds a penalty to attention weight scores that is proportional to the distance between tokens. Therefore, the attention score between two tokens i and j at every layer is calculated as:

Attention score = query_i . key_j — m.(i-j)

Where -m.(i-j) is a penalty which is proportional to the distance between token i and j. The scalar m is a head-specific slope fixed before training and its values for different heads are chosen as a geometric sequence. For example, for 8 head, m might be:

This means, the first head has a relatively large m so it penalizes far apart tokens more and focuses on recent tokens, while the 8th head has the smallest m, allowing it to attend to more distant tokens. Fig. 2 also offers visualization.

ALiBi is used in BloombergGPT and BLOOM.

Transformer Extrapolation At Inference Time:

Transformer extrapolation at inference time is the model’s ability to perform well to input sequences that are longer than those it was trained on. The transformer mechanism is agnostic to input length which means at inference time, it can work with longer sequences. However, note that the computational cost grows quadratically with input length even though the transformer layers themselves are agnostic to it.

The authors of ALiBi demonstrated that the bottleneck for transformer extrapolation is its position embedding method. As shown in Fig. 3, they compared the extrapolation capabilities of different position embedding methods. Since learned position embedding does not have a capability to encode positions greater than the training length, it has no extrapolation ability.

Fig. 3 shows that the sinusoidal position embedding in practice has very limited extrapolation capabilities. While RoPE outperforms the sinusoidal one, it still does not achieve satisfactory results. The T5 bias method (a version of relative position embedding) leads to better extrapolation than both sinusoidal and RoPE embedding. Unfortunately, the T5 bias is computationally expensive (Fig. 4). ALiBi outperforms all these position embeddings with negligible (0–0.7%) memory increase.

Conclusion:

In summary, the way positional information is being encoded in Transformer architecture significantly affects its ability to understand sequential data, especially its extrapolation at inference time. While absolute positional embedding methods provide positional awareness, they often struggle with Transformer extrapolation. That’s why newer position embeddings are proposed. Relative position encoding, RoPE, and ALiBi have the capability to extrapolate at inference time. As transformers continue to be integrated in various applications, refining position encoding is crucial to push the boundaries of their performance.

The opinions expressed in this blog post are solely our own and do not reflect those of our employer.

References:

[1] Vaswani, A. “Attention is all you need.” (2017).
[2] BERT: Devlin, Jacob. “Bert: Pre-training of deep bidirectional transformers for language understanding.” (2018).
[3] GPT: Radford, Alec, et al. “Language models are unsupervised multitask learners.” (2019).
[4] RelativePosEmb: Shaw, Peter, et al. “Self-attention with relative position representations.” (2018).
[5] Transformer-XL Dai, Zihang. “Transformer-xl: Attentive language models beyond a fixed-length context.” (2019).
[6] T5: Raffel, Colin, et al. “Exploring the limits of transfer learning with a unified text-to-text transformer.” (2020).
[7] Raffel, Colin, et al. “Exploring the limits of transfer learning with a unified text-to-text transformer.” (2020)
[8] He, Pengcheng, et al. “Deberta: Decoding-enhanced bert with disentangled attention.” (2020).
[9] RoPE: Su, Jianlin, et al. “Roformer: Enhanced transformer with rotary position embedding.” (2024).
[10] LLaMA: Touvron, Hugo, et al. “Llama: Open and efficient foundation language models.” (2023).
[11] GPT-NeoX: Black, Sid, et al. “Gpt-neox-20b: An open-source autoregressive language model.” (2022).
[12] ALiBi: Press, Ofir, et al. “Train short, test long: Attention with linear biases enables input length extrapolation.” (2021).
[13] BloombergGPT: Wu, Shijie, et al. “Bloomberggpt: A large language model for finance.” (2023).
[14] BLOOM: Le Scao, Teven, et al. “Bloom: A 176b-parameter open-access multilingual language model.” (2023).

Beyond Attention: How Advanced Positional Embedding Methods Improve upon the Original Transformers was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.