Linear Optimisations in Product Analytics

Solving the knapsack problem

It might be surprising, but in this article, I would like to talk about the knapsack problem, the classic optimisation problem that has been studied for over a century. According to Wikipedia, the problem is defined as follows:

Given a set of items, each with a weight and a value, determine which items to include in the collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

While product analysts may not physically pack knapsacks, the underlying mathematical model is highly relevant to many of our tasks. There are numerous real-world applications of the knapsack problem in product analytics. Here are a few examples:

• Marketing Campaigns: The marketing team has a limited budget and capacity to run campaigns across different channels and regions. Their goal is to maximize a KPI, such as the number of new users or revenue, all while adhering to existing constraints.
• Retail Space Optimization: A retailer with limited physical space in their stores seeks to optimize product placement to maximize revenue.
• Product Launch Prioritization: When launching a new product, the operations team’s capacity might be limited, requiring prioritization of specific markets.

Such and similar tasks are quite common, and many analysts encounter them regularly. So, in this article, I’ll explore different approaches to solving it, ranging from naive, simple techniques to more advanced methods such as linear programming.

Another reason I chose this topic is that linear programming is one of the most powerful and popular tools in prescriptive analytics — a type of analysis that focuses on providing stakeholders with actionable options to make informed decisions. As such, I believe it is an essential skill for any analyst to have in their toolkit.

Case

Let’s dive straight into the case we’ll be exploring. Imagine we’re part of a marketing team planning activities for the upcoming month. Our objective is to maximize key performance indicators (KPIs), such as the number of acquired users and revenue while operating within a limited marketing budget.

We’ve estimated the expected outcomes of various marketing activities across different countries and channels. Here is the data we have:

• country — the market where we can do some promotional activities;
• channel — the acquisition method, such as social networks or influencer campaigns;
• users — the expected number of users acquired within a month of the promo campaign;
• cs_contacts — the incremental Customer Support contacts generated by the new users;
• marketing_spending — the investment required for the activity;
• revenue — the first-year LTV generated from acquired customers.

Note that the dataset is synthetic and randomly generated, so don’t try to infer any market-related insights from it.

First, I’ve calculated the high-level statistics to get a view of the numbers.

Let’s determine the optimal set of marketing activities that maximizes revenue while staying within the $30M marketing budget.

Brute force approach

At first glance, the problem may seem straightforward: we could calculate all possible combinations of marketing activities and select the optimal one. However, it might be a challenging task.

With 62 segments, there are 2⁶² possible combinations, as each segment can either be included or excluded. This results in approximately 4.6*10¹⁸ combinations — an astronomical number.

To better understand the computational feasibility, let’s consider a smaller subset of 15 segments and estimate the time required for one iteration.

import itertools
import pandas as pd
import tqdm

# reading data
df = pd.read_csv('marketing_campaign_estimations.csv', sep = 't')
df['segment'] = df.country + ' - ' + df.channel

# calculating combinations
combinations = []
segments = list(df.segment.values)[:15]
print('number of segments: ', len(segments))

for num_items in range(len(segments) + 1):
  combinations.extend(
      itertools.combinations(segments, num_items)
  )
print('number of combinations: ', len(combinations))

tmp = []
for selected in tqdm.tqdm(combinations):
    tmp_df = df[df.segment.isin(selected)]
    tmp.append(
        {
        'selected_segments': ', '.join(selected),
        'users': tmp_df.users.sum(),
        'cs_contacts': tmp_df.cs_contacts.sum(),
        'marketing_spending': tmp_df.marketing_spending.sum(),
        'revenue': tmp_df.revenue.sum()
        }
    )

# number of segments:  15
# number of combinations:  32768

It took approximately 4 seconds to process 15 segments, allowing us to handle around 7,000 iterations per second. Using this estimate, let’s calculate the execution time for the full set of 62 segments.

2**62 / 7000 / 3600 / 24 / 365
# 20 890 800.6

Using brute force, it would take around 20.9 million years to get the answer to our question — clearly not a feasible option.

Execution time is entirely determined by the number of segments. Removing just one segment can reduce time twice. With this in mind, let’s explore possible ways to merge segments.

As usual, there are more small-sized segments than bigger ones, so merging them is a logical step. However, it’s important to note that this approach may reduce accuracy since multiple segments are aggregated into one. Despite this, it could still yield a solution that is “good enough.”

To simplify, let’s merge all segments that contribute less than 0.1% of revenue.

df['share_of_revenue'] = df.revenue/df.revenue.sum() * 100
df['segment_group'] = list(map(
    lambda x, y: x if y >= 0.1 else 'other',
    df.segment,
    df.share_of_revenue
))

print(df[df.segment_group == 'other'].share_of_revenue.sum())
# 0.53
print(df.segment_group.nunique())
# 52

With this approach, we will merge ten segments into one, representing 0.53% of the total revenue (the potential margin of error). With 52 segments remaining, we can obtain the solution in just 20.4K years. While this is a significant improvement, it’s still not sufficient.

You may consider other heuristics tailored to your specific task. For instance, if your constraint is a ratio (e.g., contact rate = CS contacts / users ≤ 5%), you could group all segments where the constraint holds true, as the optimal solution will include all of them. In our case, however, I don’t see any additional strategies to reduce the number of segments, so brute force seems impractical.

That said, if the number of combinations is relatively small and brute force can be executed within a reasonable time, it can be an ideal approach. It’s simple to develop and provides accurate results.

Naive approach: looking at top-performing segments

Since brute force is not feasible for calculating all combinations, let’s consider a simpler algorithm to address this problem.

One possible approach is to focus on the top-performing segments. We can evaluate segment performance by calculating revenue per dollar spent, then sort all activities based on this ratio and select the top performers that fit within the marketing budget. Let’s implement it.

df['revenue_per_spend'] = df.revenue / df.marketing_spending 
df = df.sort_values('revenue_per_spend', ascending = False)
df['spend_cumulative'] = df.marketing_spending.cumsum()
selected_df = df[df.spend_cumulative <= 30000000]
print(selected_df.shape[0])
# 48 
print(selected_df.revenue.sum()/1000000)
# 107.92

With this approach, we selected 48 activities and got $107.92M in revenue.

Unfortunately, although the logic seems reasonable, it is not the optimal solution for maximizing revenue. Let’s look at a simple example with just three marketing activities.

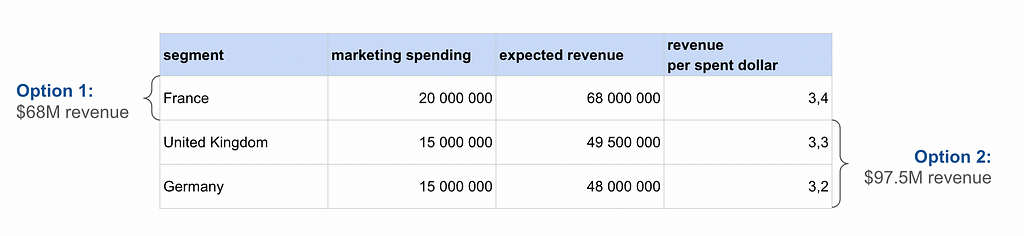
Using the top markets approach, we would select France and achieve $68M in revenue. However, by choosing two other markets, we could achieve significantly better results — $97.5M. The key point is that our algorithm optimizes not only for maximum revenue but also for minimizing the number of selected segments. Therefore, this approach will not yield the best results, especially considering its inability to account for multiple constraints.

Linear Programming

Since all simple approaches have failed, we must return to the fundamentals and explore the theory behind this problem. Fortunately, the knapsack problem has been studied for many years, and we can apply optimization techniques to solve it in seconds rather than years.

The problem we’re trying to solve is an example of Integer Programming, which is actually a subdomain of Linear Programming.

We’ll discuss this shortly, but first, let’s align on the key concepts of the optimization process. Each optimisation problem consists of:

• Decision variables: Parameters that can be adjusted in the model, typically representing the levers or decisions we want to make.
• Objective function: The target variable we aim to maximize or minimize. It goes without saying that it must depend on the decision variables.
• Constraints: Conditions placed on the decision variables that define their possible values. For example, ensuring the team cannot work a negative number of hours.

With these basic concepts in mind, we can define Linear Programming as a scenario where the following conditions hold:

• The objective function is linear.
• All constraints are linear.
• Decision variables are real-valued.

Integer Programming is very similar to Linear Programming, with one key difference: some or all decision variables must be integers. While this may seem like a minor change, it significantly impacts the solution approach, requiring more complex methods than those used in Linear Programming. One common technique is branch-and-bound. We won’t dive deeper into the theory here, but you can always find more detailed explanations online.

For linear optimization, I prefer the widely used Python package PuLP. However, there are other options available, such as Python MIP or Pyomo. Let’s install PuLP via pip.

! pip install pulp

Now, it’s time to define our task as a mathematical optimisation problem. There are the following steps for it:

• Define the set of decision variables (levers we can adjust).
• Align on the objective function (a variable that we will be optimising for).
• Formulate constraints (the conditions that must hold true during optimisations).

Let’s go through the steps one by one. But first, we need to create the problem object and set the objective — maximization in our case.

from pulp import *
problem = LpProblem("Marketing_campaign", LpMaximize)

The next step is defining the decision variables — parameters that we can change during optimisation. Our main decision is either to run a marketing campaign or not. So, we can model it as a set of binary variables (0 or 1) for each segment. Let’s do it with the PuLP library.

segments = range(df.shape[0])  
selected = LpVariable.dicts("Selected", segments, cat="Binary")

After that, it’s time to align on the objective function. As discussed, we want to maximise the revenue. The total revenue will be a sum of revenue from all the selected segments (where decision_variable = 1 ). Therefore, we can define this formula as the sum of the expected revenue for each segment multiplied by the decision binary variable.

problem += lpSum(
  selected[i] * list(df['revenue'].values)[i] 
  for i in segments
)

The final step is to add constraints. Let’s start with a simple constraint: our marketing spending must be below $30M.

problem += lpSum(
    selected[i] * df['marketing_spending'].values[i]
    for i in segments
) <= 30 * 10**6

Hint: you can print problem to double check the objective function and constraints.

Now that we’ve defined everything, we can run the optimization and analyze the results.

problem.solve()

It takes less than a second to run the optimization, a significant improvement compared to the thousands of years that brute force would require.

Result - Optimal solution found

Objective value:                110162662.21000001
Enumerated nodes:               4
Total iterations:               76
Time (CPU seconds):             0.02
Time (Wallclock seconds):       0.02

Let’s save the results of the model execution — the decision variables indicating whether each segment was selected or not — into our dataframe.

df['selected'] = list(map(lambda x: x.value(), selected.values()))
print(df[df.selected == 1].revenue.sum()/10**6)
# 110.16

It works like magic, allowing you to obtain the solution quickly. Additionally, note that we achieved higher revenue compared to our naive approach: $110.16M versus $107.92M.

We’ve tested integer programming with a simple example featuring just one constraint, but we can extend it further. For instance, we can add additional constraints for our CS contacts to ensure that our Operations team can handle the demand in a healthy way:

• The number of additional CS contacts ≤ 5K
• Contact rate (CS contacts/users) ≤ 0.042

# define the problem
problem_v2 = LpProblem("Marketing_campaign_v2", LpMaximize)

# decision variables
segments = range(df.shape[0]) 
selected = LpVariable.dicts("Selected", segments, cat="Binary")

# objective function
problem_v2 += lpSum(
  selected[i] * list(df['revenue'].values)[i] 
  for i in segments
)

# Constraints
problem_v2 += lpSum(
    selected[i] * df['marketing_spending'].values[i]
    for i in segments
) <= 30 * 10**6

problem_v2 += lpSum(
    selected[i] * df['cs_contacts'].values[i]
    for i in segments
) <= 5000

problem_v2 += lpSum(
    selected[i] * df['cs_contacts'].values[i]
    for i in segments
) <= 0.042 * lpSum(
    selected[i] * df['users'].values[i]
    for i in segments
)

# run the optimisation
problem_v2.solve()

The code is straightforward, with the only tricky part being the transformation of the ratio constraint into a simpler linear form.

Another potential constraint you might consider is limiting the number of selected options, for example, to 10. This constraint could be pretty helpful in prescriptive analytics, for example, when you need to select the top-N most impactful focus areas.

# define the problem
problem_v3 = LpProblem("Marketing_campaign_v2", LpMaximize)

# decision variables
segments = range(df.shape[0]) 
selected = LpVariable.dicts("Selected", segments, cat="Binary")

# objective function
problem_v3 += lpSum(
  selected[i] * list(df['revenue'].values)[i] 
  for i in segments
)

# constraints
problem_v3 += lpSum(
    selected[i] * df['marketing_spending'].values[i]
    for i in segments
) <= 30 * 10**6

problem_v3 += lpSum(
    selected[i] for i in segments
) <= 10

# run the optimisation
problem_v3.solve()
df['selected'] = list(map(lambda x: x.value(), selected.values()))
print(df.selected.sum())
# 10

Another possible option to tweak our problem is to change the objective function. We’ve been optimising for the revenue, but imagine we want to maximise both revenue and new users at the same time. For that, we can slightly change our objective function.

Let’s consider the best approach. We could calculate the sum of revenue and new users and aim to maximize it. However, since revenue is, on average, 1000 times higher, the results might be skewed toward maximizing revenue. To make the metrics more comparable, we can normalize both revenue and users based on their total sums. Then, we can define the objective function as a weighted sum of these ratios. I would use equal weights (0.5) for both metrics, but you can adjust the weights to give more value to one of them.

# define the problem
problem_v4 = LpProblem("Marketing_campaign_v2", LpMaximize)

# decision variables
segments = range(df.shape[0]) 
selected = LpVariable.dicts("Selected", segments, cat="Binary")

# objective Function
problem_v4 += (
    0.5 * lpSum(
        selected[i] * df['revenue'].values[i] / df['revenue'].sum()
        for i in segments
    )
    + 0.5 * lpSum(
        selected[i] * df['users'].values[i] / df['users'].sum()
        for i in segments
    )
)

# constraints
problem_v4 += lpSum(
    selected[i] * df['marketing_spending'].values[i]
    for i in segments
) <= 30 * 10**6

# run the optimisation
problem_v4.solve()
df['selected'] = list(map(lambda x: x.value(), selected.values()))

We obtained the optimal objective function value of 0.6131, with revenue at $104.36M and 136.37K new users.

That’s it! We’ve learned how to use integer programming to solve various optimisation problems.

You can find the full code on GitHub.

Summary

In this article, we explored different methods for solving the knapsack problem and its analogues in product analytics.

• We began with a brute-force approach but quickly realized it would take an unreasonable amount of time.
• Next, we tried using common sense by naively selecting the top-performing segments, but this approach yielded incorrect results.
• Finally, we turned to Integer Programming, learning how to translate our product tasks into optimization models and solve them effectively.

With this, I hope you’ve gained another valuable analytical tool for your toolkit.

Thank you a lot for reading this article. I hope this article was insightful for you. If you have any follow-up questions or comments, please leave them in the comments section.

Reference

All the images are produced by the author unless otherwise stated.

Linear Optimisations in Product Analytics was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.