NuCS: A Constraint Solver for Research, Teaching, and Production Applications

Blazing-fast constraint solving in pure Python

TLDR

NuCS is a Python library for solving Constraint Satisfaction and Optimisation Problems (CSP and COP) that I am developing as a side project. Because it is 100% written in Python, NuCS is easy to install and allows to model complex problems in a few lines of code. The NuCS solver is also very fast because it is powered by Numpy and Numba.

Many problems can be formulated as CSPs. This is why a constraint library such as NuCS can benefit a lot of developers or data scientists.

Let’s consider the famous N-queens problem which consists in placing N queens on a N x N chessboard such that the queens don’t threaten each other.

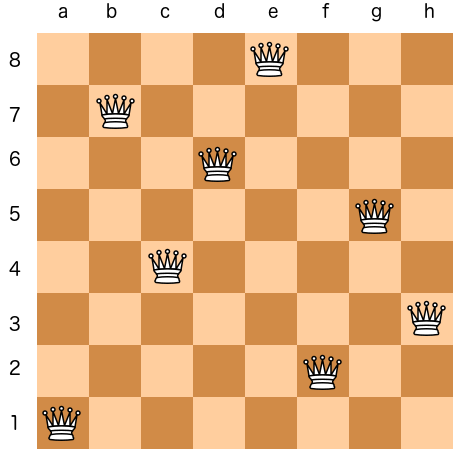
The 14200 solutions to the 12-queens problems are found in less than 2s on a MacBook Pro M2 running:

• Python 3.11,
• Numpy 2.0.1,
• Numba 0.60.0 and
• NuCS 3.0.0.

(venv) ➜  nucs git:(main) time NUMBA_CACHE_DIR=.numba/cache python -m nucs.examples.queens -n 12 --log_level=ERROR --processors=6
{
    'ALG_BC_NB': 262006,
    'ALG_BC_WITH_SHAVING_NB': 0,
    'ALG_SHAVING_NB': 0,
    'ALG_SHAVING_CHANGE_NB': 0,
    'ALG_SHAVING_NO_CHANGE_NB': 0,
    'PROPAGATOR_ENTAILMENT_NB': 0,
    'PROPAGATOR_FILTER_NB': 2269965,
    'PROPAGATOR_FILTER_NO_CHANGE_NB': 990435,
    'PROPAGATOR_INCONSISTENCY_NB': 116806,
    'SOLVER_BACKTRACK_NB': 131000,
    'SOLVER_CHOICE_NB': 131000,
    'SOLVER_CHOICE_DEPTH': 10,
    'SOLVER_SOLUTION_NB': 14200
}
NUMBA_CACHE_DIR=.numba/cache python -m nucs.examples.queens -n 12    6.65s user 0.53s system 422% cpu 1.699 total

What is constraint programming ?

Constraint programming is a paradigm for solving combinatorial problems. In constraint programming, users declaratively state the constraints on the feasible solutions for a set of decision variables. Constraints specify the properties of a solution to be found. The solver combines constraint propagation and backtracking to find the solutions.

As an example, here is a model for the Magic Sequence Problem (find a sequence x_0, … x_n-1 such that, for each i in [0, n-1], x_i is the number of occurrences of i in the sequence) using NuCS:

class MagicSequenceProblem(Problem):
    def __init__(self, n: int):
        super().__init__([(0, n)] * n)
        for i in range(n):
            self.add_propagator((list(range(n)) + [i], ALG_COUNT_EQ, [i]))
        # redundant constraints
        self.add_propagator((list(range(n)), ALG_AFFINE_EQ, [1] * n + [n]))
        self.add_propagator((list(range(n)), ALG_AFFINE_EQ, list(range(n)) + [n]))

In NuCS, a constraint is named a propagator.

The propagator (here ALG_COUNT_EQ) simply states that x_i is the number of occurrences of i in the sequence. The following two ALG_AFFINE_EQ propagators are redundant, meaning that they are not necessary for NuCS to find the solution but they speed up the resolution process.

See the documentation for a complete list of propagator supported by NuCS. Note that most propagators in NuCS are global (aka n-ary) and implement state-of-art propagation algorithms.

Python

Python is the language of choice for data scientists: it has a simple syntax, a growing community and a great number of data science and machine learning libraries.

But on the other hand, Python is known to be a slow language : maybe 50 to 100 times slower than C depending on the benchmarks.

The choice of Python for developing a high performance constraint programming library was not so obvious but we will see that the combined use of Numpy (high performance computing package) and Numba (Just-In-Time compilation for Python) helps a lot.

Many attempts have been made to write constraint solvers in Python, but these are either slow or are only wrappers and depend on external solvers written in Java or C/C++.

Numpy

NumPy brings the computational power of languages like C and Fortran to Python.

NumPy

In NuCS, everything is a Numpy array.

This allows to leverage Numpy’s indexing and broadcasting capabilities and to write compact propagators such as Max_i x_i <= y

def compute_domains_max_leq(domains: NDArray, parameters: NDArray) -> int:
  x = domains[:-1]
  y = domains[-1]
  if np.max(x[:, MAX]) <= y[MIN]:
      return PROP_ENTAILMENT
  y[MIN] = max(y[MIN], np.max(x[:, MIN]))
  if y[MIN] > y[MAX]:
      return PROP_INCONSISTENCY
  for i in range(len(x)):
      x[i, MAX] = min(x[i, MAX], y[MAX])
      if x[i, MAX] < x[i, MIN]:
          return PROP_INCONSISTENCY
  return PROP_CONSISTENCY

Numba

Numba is an open source Just-In-Time compiler that translates a subset of Python and NumPy code into fast machine code.

Numba: A High Performance Python Compiler

In the following example, we find the 14200 solutions to the 12-queens problems (note that we use a single processor here).

NUMBA_DISABLE_JIT=1 python -m nucs.examples.queens -n 12 --log_level=ERROR   179.89s user 0.31s system 99% cpu 3:00.57 total

We achieve a x60 speed-up by enabling Just-In-Time compilation:

NUMBA_CACHE_DIR=.numba/cache python -m nucs.examples.queens -n 12    3.03s user 0.06s system 99% cpu 3.095 total

In order to let Numba JIT-compile your code, you should :

• avoid OOP,
• use supported types or Numpy arrays,
• use a subset of the Python language,
• use a subset of Numpy’s functions.

In NuCS, these guidelines have been successfully implemented for :

• propagators (see https://nucs.readthedocs.io/en/latest/reference.html#propagators for the list of propagators implemented in NuCS),
• consistency algorithms (see https://nucs.readthedocs.io/en/latest/reference.html#consistency-algorithms for the list of consistency algorithms implemented in NuCS),
• heuristics (see https://nucs.readthedocs.io/en/latest/reference.html#heuristics for the list of heuristics implemented in NuCS).

Thanks to Numpy and Numba, NuCS achieves performance similar to that of solvers written in Java or C/C++.

Note that, since the Python code is compiled and the result cached, performance will always be significantly better when you run your program a second time.

Examples

NuCS comes with many models for classic constraint programming problems such as:

• some crypto-arithmetic puzzles: Alpha, Donald,
• the Balanced Incomplete Block Design problem,
• the Golomb ruler problem,
• the knapsack problem,
• the magic sequence problem,
• the magic square problem,
• the quasigroup problem,
• the n-queens problem,
• the Schur lemma problem,
• the sports tournament scheduling problem,
• the Sudoku problem.

Some of these examples require some advanced techniques:

• redundant constraints,
• custom heuristics,
• custom consistency algorithms

Most of these models are also available in CSPLib, the bible for anything CSP related.

Statistics and Logging

When solutions are searched for, NuCS also aggregates some statistics:

{
    'ALG_BC_NB': 262006,
    'ALG_BC_WITH_SHAVING_NB': 0,
    'ALG_SHAVING_NB': 0,
    'ALG_SHAVING_CHANGE_NB': 0,
    'ALG_SHAVING_NO_CHANGE_NB': 0,
    'PROPAGATOR_ENTAILMENT_NB': 0,
    'PROPAGATOR_FILTER_NB': 2269965,
    'PROPAGATOR_FILTER_NO_CHANGE_NB': 990435,
    'PROPAGATOR_INCONSISTENCY_NB': 116806,
    'SOLVER_BACKTRACK_NB': 131000,
    'SOLVER_CHOICE_NB': 131000,
    'SOLVER_CHOICE_DEPTH': 10,
    'SOLVER_SOLUTION_NB': 14200
}

Here we can see that:

• bound consistency was computed 262006 times,
• 2268895 propagators were applied but without effect 990435 times while inconsistencies were detected 116806 times,
• they were 131000 choices and backtracks, with a maximum choice depth of 10,
• finally, 14200 solutions were found.

Playing with the model and understanding how it affects the statistics has proven to be a very useful exercise in getting the most out of NuCS.

NuCS also comes with some basic logging capabilities.

NUMBA_CACHE_DIR=.numba/cache python -m nucs.examples.golomb -n 10 --symmetry_breaking --log_level=INFO

2024-11-12 17:27:45,110 - INFO - nucs.solvers.solver - Problem has 82 propagators
2024-11-12 17:27:45,110 - INFO - nucs.solvers.solver - Problem has 45 variables
2024-11-12 17:27:45,110 - INFO - nucs.solvers.backtrack_solver - BacktrackSolver uses variable heuristic 0
2024-11-12 17:27:45,110 - INFO - nucs.solvers.backtrack_solver - BacktrackSolver uses domain heuristic 0
2024-11-12 17:27:45,110 - INFO - nucs.solvers.backtrack_solver - BacktrackSolver uses consistency algorithm 2
2024-11-12 17:27:45,110 - INFO - nucs.solvers.backtrack_solver - Choice points stack has a maximal height of 128
2024-11-12 17:27:45,172 - INFO - nucs.solvers.backtrack_solver - Minimizing variable 8
2024-11-12 17:27:45,644 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 80
2024-11-12 17:27:45,677 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 75
2024-11-12 17:27:45,677 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 73
2024-11-12 17:27:45,678 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 72
2024-11-12 17:27:45,679 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 70
2024-11-12 17:27:45,682 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 68
2024-11-12 17:27:45,687 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 66
2024-11-12 17:27:45,693 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 62
2024-11-12 17:27:45,717 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 60
2024-11-12 17:27:45,977 - INFO - nucs.solvers.backtrack_solver - Found a (new) solution: 55
{
    'ALG_BC_NB': 22652,
    'ALG_BC_WITH_SHAVING_NB': 0,
    'ALG_SHAVING_NB': 0,
    'ALG_SHAVING_CHANGE_NB': 0,
    'ALG_SHAVING_NO_CHANGE_NB': 0,
    'PROPAGATOR_ENTAILMENT_NB': 107911,
    'PROPAGATOR_FILTER_NB': 2813035,
    'PROPAGATOR_FILTER_NO_CHANGE_NB': 1745836,
    'PROPAGATOR_INCONSISTENCY_NB': 11289,
    'SOLVER_BACKTRACK_NB': 11288,
    'SOLVER_CHOICE_NB': 11353,
    'SOLVER_CHOICE_DEPTH': 9,
    'SOLVER_SOLUTION_NB': 10
}
[ 1  6 10 23 26 34 41 53 55]

Customization

Finally, NuCS is a very open platform were almost anything can be customized:

• propagators,
• consistency algorithms,
• heuristics,
• solvers.

In the following Golomb ruler example, a custom consistency algorithm is registered before being used:

    consistency_alg_golomb = register_consistency_algorithm(golomb_consistency_algorithm)
    solver = BacktrackSolver(problem, consistency_alg_idx=consistency_alg_golomb)

Conclusion

In conclusion, NuCS is a constraint solver library with a lot of features. Although it is written entirely in Python, it is very fast and can be used for a wide range of applications: research, teaching and production.

Don’t hesitate to contact me on Github if you’d like to take part in NuCS development!

Some useful links to go further:

• the source code: https://github.com/yangeorget/nucs
• the documention: https://nucs.readthedocs.io/en/latest/index.html
• the Pip package: https://pypi.org/project/NUCS/

If you enjoyed this article about NuCS, please clap 50 times !

NuCS: A Constraint Solver for Research, Teaching, and Production Applications was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.