ASCVIT V1: Automatic Statistical Calculation, Visualization and Interpretation Tool

ASCVIT V1: Automatic Statistical Calculation, Visualization, and Interpretation Tool

Automated data analysis made easy: The first version of ASCVIT, the tool for statistical calculation, visualization, and interpretation

During my studies, I attended a data science seminar and came into contact with the statistical programming language R for the first time. At the time, I was fascinated by the resulting potential uses. In the meantime, the statistical evaluation of data has become easier thanks to developments in the field of machine learning. Of course, a certain level of technical understanding is required, and you need to know what certain methods actually do. It is also necessary to know what data or input is required for certain methods to work at all or deliver meaningful results. In this article, I would like to discuss the development of a first version (V1) of a local app that can be used to automatically apply various statistical methods to any datasets. This is an open source project for educational and research purposes.

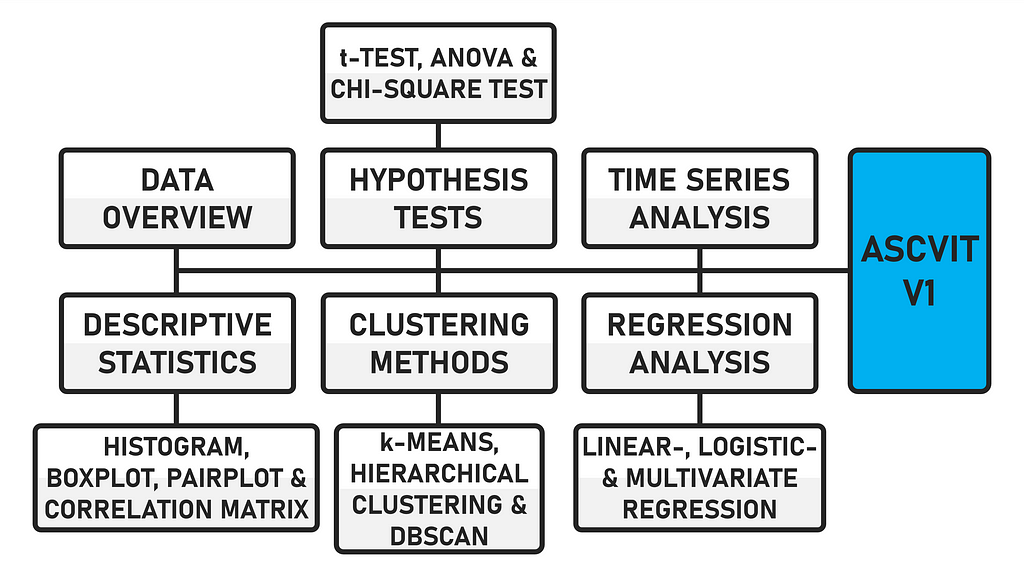
The data can be uploaded in either .csv or .xlsx format. The first version of the app provides a general data overview (data preview, data description, number of data points and categorization of variables), analyses in the field of descriptive statistics (histogram, boxplot, pairplot and correlation matrix), various hypothesis tests (t-test, ANOVA and chi-square test), regression analyses (linear, logistic and multivariate), time series analysis and supports various clustering methods (k-means, hierarchical and DBSCAN). The app is created using the Python framework Streamlit.

Due to the modular structure of the code, further statistical procedures can be easily implemented. The code is commented, which makes it easier to find your way around. When the app is executed, the interface looks like this after a dataset has been uploaded.

In addition to the automatic analysis in the various areas mentioned, a function has also been integrated that automatically analyses the statistically recorded values. The “query_llm_via_cli” function enables an exchange via CLI (command line interface) with an LLM using Ollama.

I have already explained this principle in an article published on Towards Data Science [1]. In the first version of the app, this functionality is only limited to the descriptive statistical analyses, but can also be transferred to the others. In concrete terms, this means that in addition to the automatic statistical calculation, the app also automatically interprets the data.

DATASET FOR TESTING THE APP

If you do not have your own data available, there are various sites on the internet that provide datasets free of charge. The dataset used for the development and testing of the app comes from Maven Analytics (License: ODC-BY) [2].

There are numerous free datasets on the site. The data I have examined deals with the sales figures of video games in the period from 1976 to 2024. Specifically, it is the sales figures from North America, Japan, the EU, Africa and the rest of the world. A total of 64016 titles and their rating, genre, console, etc. are recorded.

Unfortunately, not all information is available for all titles. There are many NaN (Not a Number) values that cause problems when analysed in Python or distort specific statistical analyses. I will briefly discuss the cleansing of data records below.

CLEAN UP THE DATASET

You can either clean the dataset before loading it into the app using a separate script, or you can perform the cleanup directly in the app. For the application in this article, I have implemented data cleansing directly in the app. If you want to clean up data records beforehand, you can do this using the following script.

import pandas as pd

df = pd.read_csv('YOUR .CSV FILE')
df_cleaned = df.dropna()
df_cleaned.to_csv('cleaned_file.csv', index=False)

print("Lines with missing data have been removed and saved in 'cleaned_file.csv'.")

The file is read using “pd.read_csv(‘.csv’)” and the data is saved in the DataFrame “df”. df.dropna()” removes all lines in the DataFrame that contain missing values ‘NaN’. The cleaned DataFrame is then saved in the variable “df_cleaned”. The data is saved in a new .csv file using “df_cleaned.to_csv(‘cleaned_file.csv’, index=False)”. Line indices are not saved. This is followed by an output for the successfully completed process “print(…)”. The code for this dataset cleanup can be found in the file “clean.py” and can also be downloaded later. Next, let’s move on to the actual code of the app.

LIBRARIES AND MODULES THAT ARE REQUIRED

To use the app, various libraries and modules are required, which in combination perform data visualization, statistical analysis and machine learning tasks.

import re
import subprocess

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import plotly.express as px  
import plotly.graph_objects as go  
import seaborn as sns
from matplotlib.patches import Patch
from scipy import stats
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression, LogisticRegression
from statsmodels.stats.multicomp import pairwise_tukeyhsd

import streamlit as st

A note regarding the representation of the diagrams. Some use “pyplot” (Matplotlib) and others use “plotly” (e.g. Boxplot). Even if the use of “plotly” leads to more interactive graphics, it does not make sense to use it for every type of diagram. Ultimately, the user must decide individually how the diagrams should be displayed. The code must be adapted accordingly.

The required libraries for the application can be installed using the requirements.txt file in the ZIP directory with the following command.

pip install -r requirements.txt

THE DATA OVERVIEW

The function “display_data_info()” specifically analyses the Pandas DataFrame “df” and outputs statistical key figures (mean value, standard deviation, etc.) “df.describe()”. The total number of data points (rows) of the DataFrame is output “len(df)”. Likewise, the numerical “numerical_columns” and categorical “categorical_columns” (strings) variables of the DataFrame.

The dataset has a total of 64016 data points and 6 numerical and 8 categorical variables. Before you start with certain statistical procedures, you should first look at the data. In the “Data overview” section, you can obtain various information to draw conclusions whether certain tests can be carried out at all.

For example, if there is no date variable in the dataset, no time series analysis can be carried out. If there is no binary variable, no logistic regression can be carried out. The app is already designed to ask for certain variable categories or to display error messages if incorrect values are transmitted. Next, let’s move on to descriptive statistics.

def display_data_info(df):
    st.write("**Data description:**")
    st.write(df.describe())
    st.write(f"**Number of data points:** {len(df)}")
    
    numerical_columns = df.select_dtypes(include=np.number).columns.tolist()
    categorical_columns = df.select_dtypes(include='object').columns.tolist()

    st.write("**Numerical variables:** ", ", ".join(numerical_columns))
    st.write("**Categorical variables:** ", ", ".join(categorical_columns))
    
    return numerical_columns, categorical_columns

DESCRIPTIVE STATISTICS

The “descriptive_statistics()” function allows the user to select different chart types (histogram, boxplot, pairplot and correlation matrix). A brief explanation of the type follows via “st.markdown(”“”…“”“)”. One or more numerical variables must then be selected “selected_vars”. The option whether logarithmic scaling “apply_log_scale” should be applied is available, except for the correlation matrix. Applying logarithmic scaling to a variable is particularly useful if the data is heavily distorted. The visualization is created using the corresponding diagram function.

def descriptive_statistics(df, numerical_columns):
    chart_type = st.selectbox("Select the diagram:", ["Histogram", "Boxplot", "Pairplot", "Correlation matrix"])
    
    if chart_type == "Histogram":
        st.markdown("""
        **Histogram:**
        A histogram shows the distribution of a numerical variable. It helps to 
        recognize how frequently certain values occur in the data and whether there are patterns, such as a normal distribution.
        """)
    elif chart_type == "Boxplot":
        st.markdown("""
        **Boxplot:**
        A boxplot shows the distribution of a numerical variable through its quartiles. 
        It helps to identify outliers and visualize the dispersion of the data.
        """)
    elif chart_type == "Pairplot":
        st.markdown("""
        **Pairplot:**
        A pairplot shows the relationships between different numerical variables through scatterplots.
        It helps to identify possible relationships between variables.
        """)
    elif chart_type == "Correlation matrix":
        st.markdown("""
        *Correlation matrix:**
        The correlation matrix shows the linear relationships between numerical variables.
        A positive correlation indicates that high values in one variable also correlate with high values in another.
        """)

    if chart_type in ["Pairplot", "Correlation matrix"]:
        selected_vars = st.multiselect("Select variables:", numerical_columns, default=numerical_columns)
    else:
        selected_vars = [st.selectbox("Select a variable:", numerical_columns)]
    
    if chart_type != "Correlation matrix":
        apply_log_scale = st.checkbox("Apply logarithmic scaling?", value=False)
    else:
        apply_log_scale = False 
    
    if st.button("Create diagram"):
        if chart_type == "Histogram":
            plot_histogram(df, selected_vars[0], apply_log_scale)
        elif chart_type == "Boxplot":
            plot_boxplot(df, selected_vars[0], apply_log_scale)
        elif chart_type == "Pairplot":
            plot_pairplot(df, selected_vars)
        elif chart_type == "Correlation matrix":
            plot_correlation_matrix(df, selected_vars)

THE HISTOGRAM FUNCTION

The “plot_histogram()” function is used to create the histogram depending on the variable selected by the user. At the beginning, all NaN values are removed from the variable “cleaned_data”. Various statistical key figures (mean value “mean_value”, median “median_value”, standard deviation “std_value”, minimum “min_value” and maximum “max_value” and the upper and lower end of the standard deviation) are calculated.

Since the data is interpreted by an LLM, as mentioned at the beginning, the dispersion (standard deviation in relation to the range of the data) and distribution (difference between mean and median) of the data is classified. The histogram is created “fix, ax = plt.subplots()”, vertical lines are added to increase the informative value and finally the histogram is displayed “st.pyplot(fig)”. In the case of distorted or exponential data, logarithmic scaling can be activated, whereupon the y-axis of the histogram is adjusted. The graph then looks as follows [3].

As there are no models that can read out graphics directly, we create a universal context for the analysis by the LLM. The context contains the results of the statistical calculation and additional instructions or the desired interpretation. This means that the context, which serves as input for the LLM, can be applied to any dataset.

Specifically, the input includes the aforementioned statistical key figures, an analysis of the distribution (symmetrical, right-skewed or left-skewed), an estimate of the spread (low, moderate or high) and an interpretation formatted for the LLM. Depending on the desired output, the context can be individually adapted and further specified.

The analysis is sent to the LLM “response = query_llm_via_cli(context)”, whereupon an interpretation of the histogram takes place after a short time interval, depending on the performance of the local system “st.write(f”**Histogram Interpretation:** {response}”)”.

def plot_histogram(df, variable, apply_log_scale):
    cleaned_data = df[variable].dropna()

    mean_value = cleaned_data.mean()
    median_value = cleaned_data.median()
    std_value = cleaned_data.std()
    min_value = cleaned_data.min()
    max_value = cleaned_data.max()

    std_upper = mean_value + std_value
    std_lower = max(0, mean_value - std_value)  

    concentration_range = (mean_value - std_value, mean_value + std_value)

    if std_value < (max_value - min_value) / 6:
        scatter = "low"
    elif std_value < (max_value - min_value) / 3:
        scatter = "moderate"
    else:
        scatter = "high"

    if abs(mean_value - median_value) < 0.1 * std_value:
        distribution = "symmetrical"
    elif mean_value > median_value:
        distribution = "right-skewed"
    else:
        distribution = "left-skewed"

    fig, ax = plt.subplots()
    ax.hist(cleaned_data, bins=30, edgecolor='black', alpha=0.7)

    ax.axvline(mean_value, color='red', linestyle='--', label=f'Mean: {mean_value:.2f}')
    ax.axvline(median_value, color='green', linestyle='-', label=f'Median: {median_value:.2f}')
    ax.axvline(std_upper, color='blue', linestyle=':', label=f'+1 Std: {std_upper:.2f}')
    ax.axvline(std_lower, color='blue', linestyle=':', label=f'-1 Std: {std_lower:.2f}')
    ax.set_title(f"Histogram of {variable}")
    ax.legend(title=f'Std-Deviation: {std_value:.2f}')

    if apply_log_scale:
        ax.set_yscale('log')

    st.pyplot(fig)

    context = (
        f"Here is an analysis of the distribution of the variable '{variable}':n"
        f"- Mean: {mean_value:.2f}n"
        f"- Median: {median_value:.2f}n"
        f"- Standard deviation: {std_value:.2f}n"
        f"- Minimum: {min_value:.2f}n"
        f"- Maximum: {max_value:.2f}nn"
        f"The distribution of the data shows a {distribution} distribution.n"
        f"The small difference between mean and median indicates a {distribution} distribution.n"
        f"A strong concentration of data points is observed between {concentration_range[0]:.2f} and {concentration_range[1]:.2f}.n"
        f"The scatter of the data is described as {scatter}, indicating a relatively tight distribution around the mean.nn"
        f"Please analyze this distribution in the histogram, paying particular attention to symmetry, scatter, and potential deviations.n"
        f"Avoid calling the distribution normal unless there are explicit indications.n"
        f"Use only the names of the variables {variable} in the analysis!"
    )

    response = query_llm_via_cli(context)
    st.write(f"**Histogram Interpretation:** {response}")

THE BOXPLOT FUNCTION

The “plot_boxplot()” function creates a boxplot for a variable selected by the user. Statistical key figures are calculated from the DataFrame based on the variable in order to display the distribution of the data in the diagram and to enable an analysis of the central tendency and dispersion using an LLM. In addition to the mean value, the median and the standard deviation, as with the histogram, the lower “q1”, upper “q3”, the interquartile range “iqr” (Q3 — Q1) and the lower or upper whisker “lower_whisker” and “upper_whisker”, which are based on the interquartile range (1.5 * IQR), are also determined for the boxplot.

The latter plays a role in identifying outliers and the other parameters where data is above or below a certain value. The boxplot is created using the Plotly library “fig = px.box(df, y=variable)” and finally displayed in the app “st.plotly_chart(fig)”. Logarithmic scaling can also be used for this chart type [4]. The chart then looks as follows:

As with the histogram, a context is also created for the boxplot, which is forwarded to the LLM. The statistical key figures are transmitted as well as information about potential outliers that lie outside the whisker values. The text sent to the LLM is formatted so that the analysis is performed on these metrics.

def plot_boxplot(df, variable, apply_log_scale):
    mean_value = df[variable].mean()
    median_value = df[variable].median()
    std_value = df[variable].std()
    q1 = df[variable].quantile(0.25)
    q3 = df[variable].quantile(0.75)
    iqr = q3 - q1
    lower_whisker = max(df[variable].min(), q1 - 1.5 * iqr)
    upper_whisker = min(df[variable].max(), q3 + 1.5 * iqr)

    fig = px.box(df, y=variable)
    fig.update_layout(title=f"Boxplot of {variable}")

    if apply_log_scale:
        fig.update_yaxes(type="log")  
    
    st.plotly_chart(fig)

    context = (
        f"Here is an analysis of the distribution of the variable '{variable}' based on a boxplot:n"
        f"- Mean: {mean_value:.2f}n"
        f"- Median: {median_value:.2f}n"
        f"- Standard deviation: {std_value:.2f}n"
        f"- Lower quartile (Q1): {q1:.2f}n"
        f"- Upper quartile (Q3): {q3:.2f}n"
        f"- Interquartile range (IQR): {iqr:.2f}n"
        f"- Potential outliers outside values from {lower_whisker:.2f} to {upper_whisker:.2f}.n"
        f"Please analyze this distribution and identify patterns or outliers.n"
        f"Use only the names of the variables {variable} in the analysis!"
    )

    response = query_llm_via_cli(context)
    st.write(f"**Boxplot Interpretation:** {response}")

THE PAIRPLOT FUNCTION

The “plot_pairplot()” function creates a pairplot based on the variables selected by the user. If less than two variables are selected, an error message is displayed. Scatter plots for all possible combinations of the variables and a linear regression line are displayed to show the relationships between the variables. For this to work, the regression statistics are calculated for all possible pairs of the selected variables using the “calculate_regression_stats” function. The NaN values are removed from the selected variables “selected_vars”.

A linear regression is performed between the two variables. Here, “var1” is the independent variable x and “var2” is the dependent variable y. The slope and the R2 value “r_squared” are calculated. The results are returned as a list of tuples (var1, var2, slope, r_squared). If three variables are selected [“A”, “B”, “C”], the function will calculate the regression statistics for the pairs (A, B), (A, C), (B, A), (B, C), etc. [5].

def calculate_regression_stats(df, selected_vars):
    regression_results = []
    for var1 in selected_vars:
        for var2 in selected_vars:
            if var1 != var2:
                non_nan_data = df[[var1, var2]].dropna()

                X = non_nan_data[[var1]].values.reshape(-1, 1)
                y = non_nan_data[var2].values

                if len(X) > 0 and len(y) > 0:
                    model = LinearRegression()
                    model.fit(X, y)
                    r_squared = model.score(X, y)
                    slope = model.coef_[0]

                    regression_results.append((var1, var2, slope, r_squared))

    return regression_results

def plot_pairplot(df, selected_vars):
    if len(selected_vars) > 1:
        st.write("**Pairplot with regression lines:**")
        pairplot_fig = sns.pairplot(df[selected_vars], kind='reg', diag_kind='kde', 
                                    plot_kws={'line_kws': {'color': 'red'}, 'scatter_kws': {'color': 'blue'}})
        st.pyplot(pairplot_fig.fig)

        corr_matrix = df[selected_vars].corr()
        regression_stats = calculate_regression_stats(df, selected_vars)
        correlation_list = "n".join(
            [f"The correlation between {var1} and {var2} is {corr_matrix.at[var1, var2]:.2f}."
             for var1 in corr_matrix.columns for var2 in corr_matrix.columns if var1 != var2]
        )

        regression_list = "n".join(
            [f"The regression line for {var1} and {var2} has a slope of {slope:.2f} and an R² of {r_squared:.2f}."
             for var1, var2, slope, r_squared in regression_stats]
        )

        context = (
            f"Here are the correlation and regression analyses between the selected variables:n"
            f"{correlation_list}nn"
            f"{regression_list}nn"
            f"Please analyze these relationships in detail based solely on the numerical values (correlation and regression lines).n"
            f"Use only the names of the variables {selected_vars} in the analysis!"
        )

        response = query_llm_via_cli(context)
        st.write(f"**Pairplot Interpretation:** {response}")
    else:
        st.error("At least two variables must be selected for a pairplot.")

KDE (Kernel Density Estimation) is used in the “plot_pairplot()” function for the diagonal to display the distribution of each individual variable. As with the previous functions, a context is again created for the analysis by the LLM. For this type of diagram, the LLM receives the data from the correlation and regression analysis. The text is formatted in such a way that a detailed interpretation of the relationship between the variables is generated.

THE CORRELATION MATRIX FUNCTION

The “plot_correlation_matrix” function is used to create a correlation matrix based on the variables selected by the user “if len(selected_vars) > 1”. If only one variable is selected, an error message is displayed. The visualization is done as a heatmap. The cells of the matrix are colored to show the strength and direction of the correlation. Correlations that are significant are automatically sent to the LLM for further analysis “if var1 != var2 and abs(corr_matrix.at[var1, var2]) >= 0.5”.

The linear correlation between the selected variables is displayed as the correlation coefficient (value between -1 and +1) “corr_matrix = df[selected_vars].cor()”. With a value of 0, there is no linear correlation. A value close to -1 indicates a strong negative correlation and a value close to +1 indicates a strong positive correlation. The pairs of variables and their correlation values are saved in “high_correlations” [4].

A context is created for the LLM. The existing significant correlations are classified for the textual description “correlation_list”. A strong correlation (positive or negative) is present with a value greater than 0.7. If the value is between 0.5 and 0.7, there is a moderate correlation and if the value is only just above 0.5, the correlation is weak. If no significant correlations were found, a corresponding message is displayed.

def plot_correlation_matrix(df, selected_vars):
    if len(selected_vars) > 1:
        corr_matrix = df[selected_vars].corr()

        fig, ax = plt.subplots()
        sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', ax=ax)
        ax.set_title("Correlation Matrix")
        st.pyplot(fig)

        high_correlations = []
        for var1 in corr_matrix.columns:
            for var2 in corr_matrix.columns:
                if var1 != var2 and abs(corr_matrix.at[var1, var2]) >= 0.5:  
                    if (var2, var1) not in [(v1, v2) for v1, v2, _ in high_correlations]:  
                        high_correlations.append((var1, var2, corr_matrix.at[var1, var2]))

        if high_correlations:
            correlation_list = "n".join([f"- {var1} and {var2} have a correlation value of {value:.2f}, "
                                        f"indicating a {'strong' if abs(value) > 0.7 else 'moderate' if abs(value) > 0.5 else 'weak'} correlation."
                                        for var1, var2, value in high_correlations])

            context = (
                f"Here is an analysis of the significant correlations between the selected variables in the correlation matrix:n"
                f"{correlation_list}nn"
                f"Please analyze the correlations solely based on their strength and significance.n"
                f"Use only the names of the variables {selected_vars} in the analysis!"
                f"Focus in detail on the statistical relationship and patterns."
            )

            response = query_llm_via_cli(context)
            st.write(f"**Model Response:** {response}")
        else:
            st.write("**No significant correlations were found.**")
    else:
        st.write("**The correlation matrix cannot be displayed because fewer than two variables were selected.**")

In the following statistical procedures, the interpretation of the respective key figures recorded by an LLM is not available. However, based on the previous procedure, independent implementation should not be a problem. Let us now turn to the various hypothesis tests.

HYPOTHESIS TESTS SELECTION

In the current version, three different tests (t-test, ANOVA and chi-square test) can be carried out “test_type = st.selectbox()”. Depending on the test selected, a brief explanation of its purpose appears. Depending on the area of application, this description can be expanded or removed. The t-test is used to compare the mean values of two groups. The analysis of variance (ANOVA) compares the mean value of more than two groups. The chi-square test tests the independence between two categorical variables. Depending on which test is selected, the corresponding function is performed.

T-TEST

If the user has opted for the t-test, they must select a group variable (categorical) “group_col” and a value variable (numerical) “value_col”. The group variable defines the two groups to be compared. The value variable compares the mean value between the two groups. Once the selection has been made, the names of the two groups “group1” and “group2” must be entered in a text field “st.text_input()”. The two groups should appear in the selected categorical variable. The logarithmic scaling “apply_log_scale”, which is applied to the value variable, is also available here. When the test is performed, the data of the groups is extracted and the number of data points (after the NaN values have been removed) is output. The t-statistic and the p-value are displayed.

The first value indicates the difference in the mean values between the two groups relative to the spread of the data. Whether the difference between the groups is statistically significant is indicated by the p-value. If it is less than 0.05, it is significant. To visually highlight the distribution of the two groups “filtered_df = df[df[group_col].isin([group1, group2])]”, a boxplot is created “fig, ax = plt.subplots()”. Here “pyplot” is used, alternatively you can also use “plotly” [6].

In this example, “genre” was selected as the group variable and “critic_score” as the value variable. Action (group 1) and Shooter (group 2) were defined as groups. The function also calculates whether there are significant outliers in the groups. An outlier is defined as a data point exceeding the upper quartile by more than 1.5 times the interquartile range “outliers_group1/2”. Finally, the outliers found are displayed to confirm the validity of the t-test. If the distortion is too large, this must be taken into account accordingly in order to better classify the reliability and interpretability of the test results.

def t_test(df, numerical_columns, categorical_columns):
    group_col = st.selectbox("Choose the group variable:", categorical_columns)
    value_col = st.selectbox("Choose the value variable:", numerical_columns)
    
    group1 = st.text_input("Name of group 1:")
    group2 = st.text_input("Name of group 2:")

    apply_log_scale = st.checkbox("Apply logarithmic scaling?", value=False)

    if st.button("Perform t-Test"):
        group1_data = df[df[group_col] == group1][value_col]
        group2_data = df[df[group_col] == group2][value_col]

        initial_count_group1 = len(group1_data)
        initial_count_group2 = len(group2_data)

        group1_data = group1_data.dropna()
        group2_data = group2_data.dropna()

        remaining_count_group1 = len(group1_data)
        remaining_count_group2 = len(group2_data)

        st.write(f"**Group 1 ({group1}):** Total number of data points: {initial_count_group1}, without NaN: {remaining_count_group1}")
        st.write(f"**Group 2 ({group2}):** Total number of data points: {initial_count_group2}, without NaN: {remaining_count_group2}")

        if apply_log_scale:
            group1_data = np.log1p(group1_data)
            group2_data = np.log1p(group2_data)

        if not group1_data.empty and not group2_data.empty:

            t_stat, p_value = stats.ttest_ind(group1_data, group2_data)
            st.markdown(f"**t-Statistic:** {t_stat}")
            st.markdown(f"**p-Value:** {p_value}")
            
            filtered_df = df[df[group_col].isin([group1, group2])]
            fig, ax = plt.subplots()
            sns.boxplot(x=filtered_df[group_col], y=filtered_df[value_col], ax=ax, palette="Set2")
            ax.set_title(f"Boxplot for {group1} vs. {group2}")

            if apply_log_scale:
                ax.set_yscale('log')

            st.pyplot(fig)

            outliers_group1 = group1_data[group1_data > group1_data.quantile(0.75) + 1.5 * (group1_data.quantile(0.75) - group1_data.quantile(0.25))]
            outliers_group2 = group2_data[group2_data > group2_data.quantile(0.75) + 1.5 * (group2_data.quantile(0.75) - group2_data.quantile(0.25))]

            st.write("**Outlier Analysis:**")
            if not outliers_group1.empty:
                st.write(f"In group 1 ({group1}) there are {len(outliers_group1)} outliers.")
            else:
                st.write(f"In group 1 ({group1}) there are no significant outliers.")

            if not outliers_group2.empty:
                st.write(f"In group 2 ({group2}) there are {len(outliers_group2)} outliers.")
            else:
                st.write(f"In group 2 ({group2}) there are no significant outliers.")
        else:
            st.error("One or both groups contain no data after removing NaN values.")

ANOVA-TEST

The “anova_test()” function integrates the option of performing an ANOVA test. This test checks whether there are significant differences in the mean values of several groups. The data is first cleaned “df_clean”. If the ANOVA test is significant, a Tukey’s HSD test (Honestly Significant Difference) is also carried out. At the beginning, a group variable and a value variable are again defined. If a group has fewer than 2 data points, it is excluded “valid_groups = group_sizes[group_sizes >= 2].index”.

If less than two groups remain after the adjustment, an error message is displayed and the test is not performed. The ANOVA test calculates the F-value and the p-value. The variability between the groups compared to the variability within the group is measured by the F-value. Whether the difference between the mean values of the group is significant is indicated by the p-value. If the value is less than 0.05, at least one group is significantly different. To visualize the results, a boxplot is created using “pyplot” [7].

If the ANOVA test produces significant results, a Tukey’s test is carried out to examine the differences between the individual group pairs in concrete terms. The ANOVA test therefore does not show which groups differ from each other. A diagram is created that shows the pairwise mean differences between the groups and their confidence interval “st.pyplot(tukey.plot_simultaneous())”.

Below the diagram, the results are displayed in a table “st.dataframe(tukey_results_df, height=400)”. The table contains the two groups, the mean difference “meandiff”, the adjusted p-value “p-adj”, the confidence interval and whether the null hypothesis can be rejected or not “reject” (True = significant, Fals = not significant). A brief example of the confidence interval. For the 3DS and GBA consoles, the interval lies between -0.9319 and -0.0061 and is therefore completely below zero. The difference in the mean value is significant.

The key figures can be used to have the results interpreted by an LLM. There is also an option to download the data as a .csv file for further statistical analyses (e.g. regression analyses) [7].

def anova_test(df, numerical_columns, categorical_columns):
    group_col = st.selectbox("Choose the group variable:", categorical_columns)
    value_col = st.selectbox("Choose the value variable:", numerical_columns)

    if st.button("Perform ANOVA"):
        df_clean = df[[group_col, value_col]].dropna()

        group_sizes = df_clean.groupby(group_col).size()
        valid_groups = group_sizes[group_sizes >= 2].index
        df_filtered = df_clean[df_clean[group_col].isin(valid_groups)]

        if len(valid_groups) < 2:
            st.error("After removing small groups, there are not enough groups left for the ANOVA test.")
        else:
            grouped_data = [group[value_col].values for name, group in df_filtered.groupby(group_col)]
            try:
                anova_result = stats.f_oneway(*grouped_data)
                st.markdown(f"**F-Value:** {anova_result.statistic}")
                st.markdown(f"**p-Value:** {anova_result.pvalue}")

                fig, ax = plt.subplots(figsize=(10, 6))
                sns.boxplot(x=group_col, y=value_col, data=df_filtered, ax=ax)
                plt.xticks(rotation=90)
                st.pyplot(fig)

                if anova_result.pvalue < 0.05:
                    st.write("The ANOVA test is significant. Tukey's HSD test will be performed.")
                    try:
                        tukey = pairwise_tukeyhsd(endog=df_filtered[value_col], groups=df_filtered[group_col], alpha=0.05)
                        st.pyplot(tukey.plot_simultaneous())

                        tukey_results_df = pd.DataFrame(data=tukey.summary().data[1:], columns=tukey.summary().data[0])
                        st.write("Results of the Tukey HSD test:")
                        st.dataframe(tukey_results_df, height=400)

                        csv = tukey_results_df.to_csv(index=False)
                        st.download_button(label="Download Tukey HSD results as CSV", data=csv, file_name='tukey_hsd_results.csv', mime='text/csv')

                    except Exception as e:
                        st.error(f"An error occurred during Tukey's HSD test: {str(e)}")

            except ValueError as e:
                st.error(f"An error occurred: {str(e)}.")

CHI-QUADRAT-TEST

The “chi_square_test()” function checks whether there is a statistically significant relationship between two categorical variables. As only categorical variables can be used, the option to activate logarithmic scaling is not required. Specifically, whether the frequency of observations in the categories is independent of each other or whether there is a correlation. The user selects two of the existing categorical variables. The NaN values are removed and only the top 10 most frequent categories are selected for each variable in order to keep the analysis manageable “value_counts().nlargest(10).index”.

A crosstab “contingency_table” is created, which shows the frequencies of the combinations of categories in the two selected variables using a heatmap. If the crosstab is not valid (too little data or only one category), the test is not performed [8].

The test calculates various values. The chi-square value “chi2” determines the measure of the difference between the observed and expected frequencies. A strong difference is present with high values. As with the other analyses, the p-value “p” shows whether the difference is significant. The number of degrees of freedom of the test “dof” is indicated as well as the expected frequencies “expected”.

def chi_square_test(df, categorical_columns):
    cat_var1 = st.selectbox("Choose the first group variable:", categorical_columns)
    cat_var2 = st.selectbox("Choose the second group variable:", categorical_columns)
    
    if st.button("Perform Chi-square test"):
        df_clean = df[[cat_var1, cat_var2]].dropna()

        top_cat_var1 = df_clean[cat_var1].value_counts().nlargest(10).index
        top_cat_var2 = df_clean[cat_var2].value_counts().nlargest(10).index
        df_filtered = df_clean[df_clean[cat_var1].isin(top_cat_var1) & df_clean[cat_var2].isin(top_cat_var2)]

        try:
            contingency_table = pd.crosstab(df_filtered[cat_var1], df_filtered[cat_var2])

            if contingency_table.empty or contingency_table.shape[0] < 2 or contingency_table.shape[1] < 2:
                st.error("The contingency table is invalid. Check the variables.")
            else:
                chi2, p, dof, expected = stats.chi2_contingency(contingency_table)
                st.markdown(f"**Chi-square:** {chi2}")
                st.markdown(f"**p-Value:** {p}")
                
                st.write("**Heatmap of the contingency table:**")
                fig, ax = plt.subplots(figsize=(12, 10))  # Larger display
                sns.heatmap(contingency_table, annot=False, cmap="YlGnBu", ax=ax)
                ax.set_title(f"Heatmap of the contingency table: {cat_var1} vs. {cat_var2} top 10")
                plt.xticks(rotation=90)
                st.pyplot(fig)

        except ValueError as e:
            st.error(f"An error occurred: {str(e)}.")

REGRESSION ANALYSIS SELECTION

The selection of the available regression analyses (linear, logistic and multivariate) is similar to the selection of the various hypothesis tests. Once an analysis method has been selected, a brief explanation is displayed and the corresponding function is called up.

LINEAR REGRESSION ANALYSIS

At the beginning of the “linear_regression()” function, a correlation matrix is created from all available numerical variables in the uploaded dataset “corr_matrix = df[numerical_columns].corr()”. The matrix is intended to help the user understand the relationships between the variables in order to identify the variables for which regression analyses are appropriate and those for which they are not (multicollinearity).

Finally, the dependent variable and one or more independent variables are selected. The data is cleaned and a linear regression model is created for all selected independent variables “model = LinearRegression()”. The regression coefficient and the intercept are specified. After the overall model has been run, a separate linear regression model is created for each independent variable and represented by a scatterplot [9].

The regression coefficient shown indicates the extent to which the dependent variable is changed when the respective independent variable is changed by one unit. Assuming that all other variables remain constant. The value that the dependent variable assumes when all independent variables are zero is indicated by the intercept.

def linear_regression(df, numerical_columns):
    st.write("**Correlation matrix of numerical variables:**")
    corr_matrix = df[numerical_columns].corr()
    fig, ax = plt.subplots(figsize=(10, 8))
    sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', ax=ax)
    st.pyplot(fig)

    dependent_var = st.selectbox("Choose the dependent variable:", numerical_columns)
    independent_vars = st.multiselect("Choose the independent variables:", numerical_columns)

    if independent_vars:
        if st.button("Perform regression"):
            X = df[independent_vars].dropna()
            y = df[dependent_var].loc[X.index]
            y = y.dropna()
            X = X.loc[y.index]

            if y.isnull().values.any():
                st.error("The dependent variable still contains missing values. Please clean the data.")
            else:
                model = LinearRegression()
                model.fit(X, y)

                st.markdown("**Regression coefficients:**")
                for var, coef in zip(independent_vars, model.coef_):
                    st.write(f"- {var}: {coef}")
                st.write(f"**Intercept:** {model.intercept_}")

                for var in independent_vars:
                    X_single_var = X[[var]]  # Use only the current independent variable
                    model_single = LinearRegression()
                    model_single.fit(X_single_var, y)

                    fig, ax = plt.subplots()
                    ax.scatter(X[var], y, edgecolor='none', facecolors='blue', s=5, label='Data points')

                    ax.plot(X[var], model_single.predict(X_single_var), color='red', label='Regression line')
                    ax.set_xlabel(var)
                    ax.set_ylabel(dependent_var)
                    ax.set_title(f"{dependent_var} vs {var}")
                    ax.legend()
                    st.pyplot(fig)

THE LOGISTIC REGRESSION ANALYSIS

As with the other functions, the user selects dependent and independent variables at the beginning. In this analysis method, the dependent variable must be binary (0/1). To demonstrate the function, I have created some data that has nothing to do with the dataset used so far. Alternatively, you can also manually adjust the values of variables, as long as there are not too many categories. If an incorrect variable is selected, a corresponding error message is displayed.

If everything is defined correctly, the logistic regression is performed and the model uses the independent variables to model the probability for the target variable. Specifically, this is the probability that an event will occur. The coefficients are specified for each independent variable and the logistic function is visualized. This shows how the probability of the target result (1 instead of 0) changes when the independent variable changes [10].

In the scatterplot, the red line represents the prediction probability for the target result, i.e. the probability that result 1 will occur. The independent variable varies. The “logistic_regression()” function is very well suited to binary classification problems where you want to predict the occurrence of an event based on several factors.

def logistic_regression(df, numerical_columns):
    dependent_var = st.selectbox("Choose the dependent variable (binary):", numerical_columns)
    independent_vars = st.multiselect("Choose the independent variables:", numerical_columns)

    if independent_vars:
        if st.button("Perform logistic regression"):
            X = df[independent_vars].dropna()
            y = df[dependent_var].loc[X.index].dropna()
            X = X.loc[y.index]

            unique_values = y.unique()
            if len(unique_values) != 2:
                st.error("The dependent variable must be binary (e.g., 0 and 1).")
            else:
                model = LogisticRegression()
                model.fit(X, y)

                st.write("**Logistic regression coefficients:**")
                for var, coef in zip(independent_vars, model.coef_[0]):
                    st.write(f"- {var}: {coef}")
                st.write(f"**Intercept:** {model.intercept_[0]}")

                for var in independent_vars:
                    fig, ax = plt.subplots()

                    ax.scatter(X[var], y, label='Data points')
                    x_range = np.linspace(X[var].min(), X[var].max(), 300).reshape(-1, 1)
                    X_copy = pd.DataFrame(np.tile(X.mean().values, (300, 1)), columns=X.columns)
                    X_copy[var] = x_range.flatten()  # Vary the current variable var
                    y_prob = model.predict_proba(X_copy)[:, 1]

                    ax.plot(x_range, y_prob, color='red', label='Logistic function')
                    ax.set_xlabel(var)
                    ax.set_ylabel(f'Probability ({dependent_var})')
                    ax.set_title(f'Logistic regression: {dependent_var} vs {var}')
                    ax.legend()
                    st.pyplot(fig)

MULTIVARIATE REGRESSION ANALYSIS

In multivariate regression analysis, the user must select several dependent variables and one or more independent variables. The analysis examines how the dependent variables are influenced by the independent variables. After the variable selection, the NaN values are removed again and an error message is displayed if necessary. The model outputs the regression coefficient and the intercept for all dependent variables.

A scatterplot with regression line is created for all combinations of independent and dependent variables. This function makes it possible to analyze several target variables simultaneously and to model their relationship to several predictors [11].

def multivariate_regression(df, numerical_columns):
    dependent_vars = st.multiselect("**Choose the dependent variables (multiple):**", numerical_columns)
    independent_vars = st.multiselect("**Choose the independent variables:**", numerical_columns)

    if dependent_vars and independent_vars:
        if st.button("Perform multivariate regression"):
            X = df[independent_vars].dropna()
            Y = df[dependent_vars].loc[X.index].dropna()
            X = X.loc[Y.index]

            if X.shape[1] != len(independent_vars) or Y.shape[1] != len(dependent_vars):
                st.error("The number of independent or dependent variables does not match.")
                return

            model = LinearRegression()
            model.fit(X, Y)

            st.write("**Multivariate regression coefficients:**")
            for i, dep_var in enumerate(dependent_vars):
                st.write(f"nFor the dependent variable: **{dep_var}**")
                st.write(f"Intercept: {model.intercept_[i]}")
                for var, coef in zip(independent_vars, model.coef_[i]):
                    st.write(f"- {var}: {coef}")

            for dep_var in dependent_vars:
                for var in independent_vars:
                    fig, ax = plt.subplots()
                    ax.scatter(X[var], Y[dep_var], label='Data points')

                    x_range = np.linspace(X[var].min(), X[var].max(), 300).reshape(-1, 1)
                    X_copy = pd.DataFrame(np.tile(X.mean().values, (300, 1)), columns=X.columns)
                    X_copy[var] = x_range.flatten()

                    y_pred = model.predict(X_copy)

                    ax.plot(x_range, y_pred[:, dependent_vars.index(dep_var)], color='red', label='Regression line')
                    ax.set_xlabel(var)
                    ax.set_ylabel(dep_var)
                    ax.set_title(f'Multivariate regression: {dep_var} vs {var}')
                    ax.legend()
                    st.plotly_chart(fig)

THE TIME SERIES ANALYSIS

This analysis method performs an analysis over time. For this purpose, a given time series is grouped by year and the annual average of a value is calculated and displayed. A time variable is required for the analysis; if the dataset used does not contain one, it cannot be performed. In the dataset I have selected, there is the variable “release_date”, which contains the release date of the respective game.

The selected time variable is converted to the date format “df[time_var]”. If the data points are invalid, they are converted to NaN values and removed “df = df.dropna(subset=[time_var])”. The data is then grouped by year “df[‘year’] = df[time_var].dt.year” and the annual average for the specified value variable “value_var” is calculated “yearly_avg”. The minimum and maximum annual average values of the value variable are calculated as well as the overall average across all data points “overall_avg”. The annual average of the value variable per year is then displayed via a line chart. The overall average is integrated on the horizontal line. The values are displayed alternately above and below the data points to improve readability [12].

Important statistical key figures are displayed below the diagram, which can be easily interpreted as in the descriptive analysis using an LLM. Specifically, the standard deviation, the variance and the minimum and maximum of the value variable as well as the year are displayed. The “perform_time_series_analysis()” function is suitable for analyzing time trends in a data series. This allows an initial analysis of the variability over time.

def perform_time_series_analysis(df, time_var, value_var):
    df[time_var] = pd.to_datetime(df[time_var], errors='coerce')
    df = df.dropna(subset=[time_var])

    if df.empty:
        st.error("**Error:** The time variable has an incorrect format.")
    else:
        df['year'] = df[time_var].dt.year
        yearly_avg = df.groupby('year')[value_var].mean().reset_index()

        y_min = yearly_avg[value_var].min()
        y_max = yearly_avg[value_var].max()
        y_range = y_max - y_min
        y_buffer = y_range * 0.05

        overall_avg = df[value_var].mean()

        fig, ax = plt.subplots(figsize=(10, 6))
        ax.plot(yearly_avg['year'], yearly_avg[value_var], marker='o', label='Yearly average')
        ax.axhline(overall_avg, color='red', linestyle='--', label=f'Overall average: {overall_avg:.2f}')
        ax.set_title(f'Average {value_var} per year')
        ax.set_xlabel('Year')
        ax.set_ylabel(f'Average {value_var}')
        ax.set_ylim(y_min - y_buffer, y_max + y_buffer)

        ax.text(yearly_avg['year'].max() - (yearly_avg['year'].max() - yearly_avg['year'].min()) * 0.05, 
                overall_avg + y_buffer, 
                f'{overall_avg:.2f}', color='red', ha='right', va='center')

        for i in range(len(yearly_avg)):
            if i % 2 == 0:
                ax.text(yearly_avg['year'][i], yearly_avg[value_var][i] + y_buffer/2, 
                        f'{yearly_avg[value_var][i]:.2f}', color='blue', ha='center', va='bottom')
            else:
                ax.text(yearly_avg['year'][i], yearly_avg[value_var][i] - y_buffer/2, 
                        f'{yearly_avg[value_var][i]:.2f}', color='blue', ha='center', va='top')

        plt.xticks(rotation=45)
        ax.legend()
        st.pyplot(fig)

        st.write(f"**Standard deviation:** {df[value_var].std():.2f}")
        st.write(f"**Variance:** {df[value_var].var():.2f}")
        st.write(f"**Minimum {value_var}:** {y_min:.2f} in year {yearly_avg.loc[yearly_avg[value_var].idxmin(), 'year']}")
        st.write(f"**Maximum {value_var}:** {y_max:.2f} in year {yearly_avg.loc[yearly_avg[value_var].idxmax(), 'year']}")

CLUSTERING METHOD SELECTION

As with the hypothesis tests and regression analyses, there are also various options to choose from in the area of clustering methods. The selection function has a similar structure to the others. A method is selected and the corresponding function is executed. A brief explanation of the method is also shown here. Depending on the method, the number of clusters must be defined. For k-Means and hierarchical clustering, a maximum of 10 clusters can be defined. For DBSCAN, the radius “eps” and the minimum number of points per cluster “min_samples” are queried. At least two numerical variables must be selected for each method.

k-MEANS CLUSTERING

The k-Means algorithm divides the data into “n_clusters”. The points are grouped in such a way that the distance between the points within the cluster is minimized. The number of clusters is determined by the user. Depending on the number, the algorithm calculates which data points belong to which cluster. The result is sent to the “visualize_clusters()” function for visualization [13].

def perform_kmeans(X, n_clusters):
    kmeans = KMeans(n_clusters=n_clusters, random_state=42)
    X['Cluster'] = kmeans.fit_predict(X)
    
    visualize_clusters(X, 'k-Means Clustering')

HIERARCHICAL CLUSTERING

A hierarchy of clusters is created here, whereby agglomerative or divisive methods can be used. Agglomerative clustering is used in the function, whereby each data point is initially considered as a separate cluster before they are successively merged. The number of clusters is determined by the user and the algorithm divides the data according to the number. The same function as for k-Means is used for visualization “visualize_clusters(X, ‘Hierarchical Clustering’)” [14].

def perform_hierarchical_clustering(X, n_clusters):
    hierarchical_clustering = AgglomerativeClustering(n_clusters=n_clusters)
    X['Cluster'] = hierarchical_clustering.fit_predict(X)
       
    visualize_clusters(X, 'Hierarchical Clustering')

DBSCAN CLUSTERING

With this method, data points are grouped based on the density of their surroundings. The method is well suited to detecting outliers (noise) and finding clusters of any shape. Here, the user does not specify the number of clusters, but the maximum distance “eps” between two points before they are considered neighbors. The minimum number of points that occur in a cluster “min_samples” is also defined. The visualization is also created by “visualize_clusters()” [15].

def perform_dbscan(X, eps, min_samples):
    dbscan = DBSCAN(eps=eps, min_samples=min_samples)
    X['Cluster'] = dbscan.fit_predict(X)
    
    visualize_clusters(X, 'DBSCAN Clustering')

CLUSTER VISUALIZATION

The results of the three different clustering methods are visualized in the “visualize_clusters” function using Principal Component Analysis (PCA). The dimensions of the data are reduced by PCA to two components “n_components” in order to be able to display the clusters. It is checked whether there are enough data points and variables “num_samples”; if this is not the case, an error message is displayed. The clusters are visualized by a scatterplot that shows the data points in the first two PCA components.

The clusters are displayed in different colors “cmap=‘tab10’”. In the diagrams, the axis label “ax.set_x/ylabel” and the legend “legend_labels” are adapted for better interpretation. The size of the data points “s” and the transparency “alpha” have also been adjusted to improve visibility. Outliers are automatically assigned to cluster -1 in DBSCAN. A table with the average values of the variable for each cluster is displayed below the visualization “st.dataframe(cluster_means)”.

def visualize_clusters(X, title):
    num_samples, num_features = X.shape
    
    n_components = min(num_samples, num_features, 2) 

    if n_components < 2:
        st.error("Not enough data points or variables to perform PCA.")
        return

    pca = PCA(n_components=n_components)
    
    try:
        X_pca = pca.fit_transform(X.drop(columns=['Cluster']))
        
        fig, ax = plt.subplots(figsize=(10, 6))
        scatter = ax.scatter(X_pca[:, 0], X_pca[:, 1], c=X['Cluster'], cmap='tab10', s=25, alpha=0.4)
        
        ax.set_title(title)
        ax.set_xlabel(f'PCA 1' if n_components >= 1 else '')
        ax.set_ylabel(f'PCA 2' if n_components == 2 else '')

        cluster_counts = X['Cluster'].value_counts()  

        legend_labels = [f"Cluster {int(cluster)} ({count} points)" for cluster, count in cluster_counts.items()]
        legend1 = ax.legend(handles=scatter.legend_elements()[0], labels=legend_labels)
        ax.add_artist(legend1)

        st.pyplot(fig)

        st.write(f"**Average values per cluster:**")
        cluster_means = X.groupby('Cluster').mean()
        st.dataframe(cluster_means)

    except ValueError as e:
        st.error(f"**Error:** Not enough variables were selected.")

COMMUNICATION WITH THE LLM

In this first version of the app, the output of the statistical calculations is only analyzed in the descriptive area. The key figures are interpreted using the “query_llm_via_cli” function. Specifically, the function is used to communicate with the LLM via a command line (CLI). To achieve this, the Python module “subprocess” is used to start the process via the command line. The LLM is started via the command [“ollama”, “run”, “llama3.1”]. The input is stored in “stdin”, the output in “stout”.

Errors and warnings are stored in “stderr”, which hopefully do not occur. The input is sent to the model via “process.communicate”. Specifically, the created “context” is sent to the function to communicate with the LLM. If there is no response from the model, a timeout mechanism “timeout=40” is included, which stops the execution after 40 seconds. Depending on the computing power of the system used, a response from the model should be displayed much earlier. The model’s response is cleaned up and passed to “extract_relevant_answer” in order to extract relevant information [1].

def query_llm_via_cli(input_text):
    """Sends the question and context to the LLM and receives a response"""
    try:
        process = subprocess.Popen(
            ["ollama", "run", "llama3.1"],
            stdin=subprocess.PIPE,
            stdout=subprocess.PIPE,
            stderr=subprocess.PIPE,
            text=True,
            encoding='utf-8',
            errors='ignore',
            bufsize=1
        )
        stdout, stderr = process.communicate(input=f"{input_text}n", timeout=40)

        if process.returncode != 0:
            return f"Error in the model request: {stderr.strip()}"

        response = re.sub(r'x1b[.*?m', '', stdout)
        return extract_relevant_answer(response)

    except subprocess.TimeoutExpired:
        process.kill()
        return "Timeout for the model request"
    except Exception as e:
        return f"An unexpected error has occurred: {str(e)}"

def extract_relevant_answer(full_response):
    response_lines = full_response.splitlines()
    if response_lines:
        return "n".join(response_lines).strip()
    return "No answer received"

MAIN FUNCTION OF THE APP

The structure of the app is defined by the “main()” function. The title is set “st.title()” and the sidebar for uploading the dataset in CSV or Excel format “uploaded_file” is submitted. Once a file has been uploaded, it is analyzed and the numerical and categorical variables are extracted. Here and in many other situations, “session_state” is used by Streamlit to store certain parameters that are relevant for the selection in the analysis methods.

The variables “numerical_columns” and “categorical_columns” are updated as soon as a new dataset is uploaded. Once data is available, the user can select from the various analysis methods. Once a method has been selected, it is displayed and can be carried out after the corresponding variables have been defined. The main function controls the interactive statistical analysis of the app.

CUSTOMIZATION OPTIONS

As already mentioned, the app can be expanded to include other analysis methods due to the modular structure of the code. The functionality of interpreting statistical key figures using an LLM can also be transferred to other methods. Llama3.1 (8B) from Meta is currently used, but another LLM (e.g. Mistral) from Ollama can also be used. The command in the “query_llm_via_cli” function must then be adapted accordingly.

Depending on the available power, models with more parameters can also be used. The design of the diagrams can be further refined, as can the transmitted contexts, in order to improve the output of the LLM. Alternatively, you can also create a new model file to adjust certain parameters (e.g. parameters) of the LLM and thereby improve the interpretation of the data.

ASCVIT V1 PYTHON SCRIPT [GITHUB]

The app code can be downloaded from the following GitHub repository. The app is started in the corresponding directory using the following command:

Streamlit run app.py

CONCLUSION

In this article, I showed how Streamlit can be used to create an app that can be used to analyze datasets using various methods. I also showed how an interpretation can be integrated into the app using an LLM, which results in real added value. Data is not only automatically visualized and statistical parameters are output, but also classified. The application offers a lot of potential for further development. I have listed some suggestions in the penultimate section. Have fun using and customizing the app.

[1] Pietrusky, S. (2024, August 21). How to talk to a PDF file without using proprietary models: CLI, Streamlit, Ollama. Towards Data Science. URL

[2] Maven Analytics. (2024, Juni 10.). Data Playground, Video Game Sales. URL

[3] Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: Data mining, inference, and prediction (2nd ed.). Stanford University. URL

[4] Bruce, P., Bruce, A., & Gedeck, P. (2021). Praktische Statistik für Data Scientists: 50+ essenzielle Konzepte mit R und Python (2nd ed.). O’Reilly.

[5] VanderPlas J. (2017). Python Data Science Handbook: Essential Tools for Working with Data. O’Reilly. URL

[6] Fahrmeir, L., Künstler, R., Pigeot, I., & Tutz, G. (2016). Statistik: Der Weg zur Datenanalyse (8th ed.). Springer.

[7] Montgomery, D. C. (2012). Design and analysis of experiments (8th ed.). Wiley. URL

[8] Moore, D. S., McCabe, G. P., Craig, B. A., & Duckworth, W. M. (2021). Introduction to the practice of statistics (10th ed.). W. H. Freeman.

[9] Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to linear regression analysis (5th ed.). Wiley. URL

[10] Hosmer, D. W., Lemeshow, S., & Sturdivant, R. X. (2013). Applied logistic regression (3rd ed.). Wiley.

[11] Johnson, R. A., & Wichern, D. W. (2007). Applied multivariate statistical analysis (6th ed.). Pearson. URL

[12] Box, G. E. P., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis: Forecasting and control (5th ed.). Wiley. URL

[13] Witten, I. H., & Frank, E. (2005). Data mining: Practical machine learning tools and techniques (2nd ed.). Morgan Kaufmann.URL

[14] Everitt, B. S., Landau, S., Leese, M., & Stahl, D. (2011). Cluster analysis (5th ed.). Wiley. URL

[15] Aggarwal, C. C., & Reddy, C. K. (2014). Data Clustering: Algorithms and Applications. CRC Press URL

ASCVIT V1: Automatic Statistical Calculation, Visualization and Interpretation Tool was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.