Introducing Semantic Tag Filtering: Enhancing Retrieval with Tag Similarity

Semantic Tag Filtering

How to use Semantic Similarity to improve tag filtering

***To understand this article, the knowledge of both Jaccard similarity and vector search is required. The implementation of this algorithm has been released on GitHub and is fully open-source.

Over the years, we have discovered how to retrieve information from different modalities, such as numbers, raw text, images, and also tags.
With the growing popularity of customized UIs, tag search systems have become a convenient way of easily filtering information with a good degree of accuracy. Some cases where tag search is commonly employed are the retrieval of social media posts, articles, games, movies, and even resumes.

However, traditional tag search lacks flexibility. If we are to filter the samples that contain exactly the given tags, there might be cases when, especially for databases containing only a few thousand samples, there might not be any (or only a few) matching samples for our query.

***Through the following article I am trying to introduce several new algorithms that, to the extent of my knowledge, I have been unable to find. I am open to criticism and welcome any feedback.

How does traditional tag search work?

Traditional systems employ an algorithm called Jaccard similarity (commonly executed through the minhash algo), which is able to compute the similarity between two sets of elements (in our case, those elements are tags). As previously clarified, the search is not flexible at all (sets either contain or do not contain the queried tags).

Can we do better?

What if, instead, rather than just filtering a sample from matching tags, we could take into account all the other labels in the sample that are not identical, but are similar to our chosen tags? We could be making the algorithm more flexible, expanding the results to non-perfect matches, but still good matches. We would be applying semantic similarity directly to tags, rather than text.

Introducing Semantic Tag Search

As briefly explained, this new approach attempts to combine the capabilities of semantic search with tag filtering systems. For this algorithm to be built, we need only one thing:

• A database of tagged samples

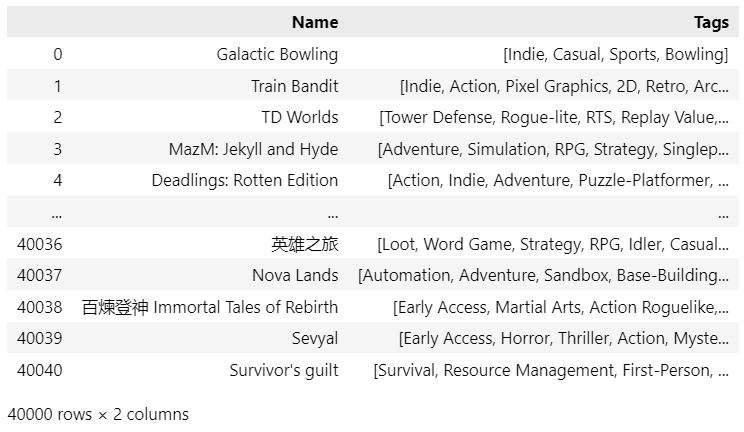
The reference data I will be using is the open-source collection of the Steam game library (downloadable from Kaggle — MIT License) — approx. 40,000 samples, which is a good amount of samples to test our algorithm. As we can see from the displayed dataframe, each game has several assigned tags, with over 400 unique tags in our database.

Now that we have our starting data, we can proceed: the algorithm will be articulated in the following steps:

1. Extracting tags relationships
2. Encoding queries and samples
3. Perform the semantic tag search using vector retrieval
4. Validation

In this article, I will only explore the math behind this new approach (for an in-depth explanation of the code with a working demo, please refer to the following notebook: instructions on how to use simtag are available in the README.md file on root).

1. Extracting tag relationships

The first question that comes to mind is how can we find the relationships between our tags. Note that there are several algorithms used to obtain the same result:

• Using statistical methods
  The simplest employable method we can use to extract tag relationships is called co-occurrence matrix, which is the format that (for both its effectiveness and simplicity) I will employ in this article.
• Using Deep Learning
  The most advanced ones are all based on Embeddings neural networks (such as Word2Vec in the past, now it is common to use transformers, such as LLMs) that can extract the semantic relationships between samples. Creating a neural network to extract tag relationships (in the form of an autoencoder) is a possibility, and it is usually advisable when facing certain circumstances.
• Using a pre-trained model
  Because tags are defined using human language, it is possible to employ existing pre-trained models to compute already existing similarities. This will likely be much faster and less troubling. However, each dataset has its uniqueness. Using a pre-trained model will ignore the customer behavior.
  Ex. We will later see how 2D has a strong relationship with Fantasy: such a pair will never be discovered using pre-trained models.

The choice of the algorithm may depend on many factors, especially when we have to work with a huge data pool or we have scalability concerns (ex. # tags will equal our vector length: if we have too many tags, we need to use Machine Learning to stem this problem.

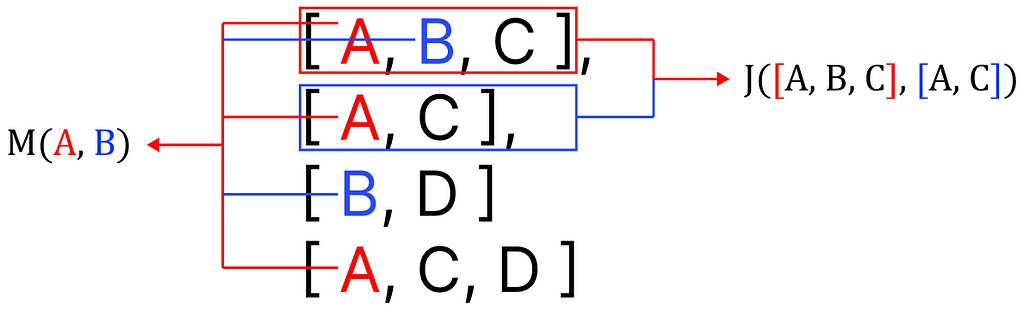
a. Build co-occurence matrix using Michelangiolo similarity

As mentioned, I will be using the co-occurrence matrix as a means to extract these relationships. My goal is to find the relationship between every pair of tags, and I will be doing so by applying the following count across the entire collection of samples using IoU (Intersection over Union) over the set of all samples (S):

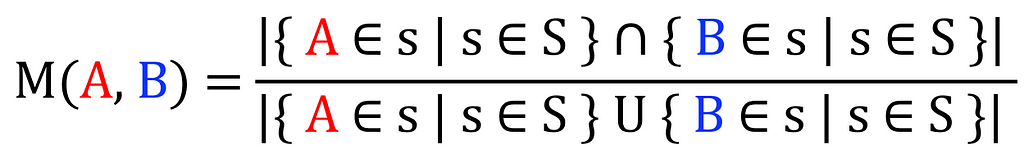
This algorithm is very similar to Jaccard similarity. While it operates on samples, the one I introduce operates on elements, but since (as of my knowledge) this specific application has not been codified, yet, we can name it Michelangiolo similarity. (To be fair, the use of this algorithm has been previously mentioned in a StackOverflow question, yet, never codified).

For 40,000 samples, it takes about an hour to extract the similarity matrix, this will be the result:

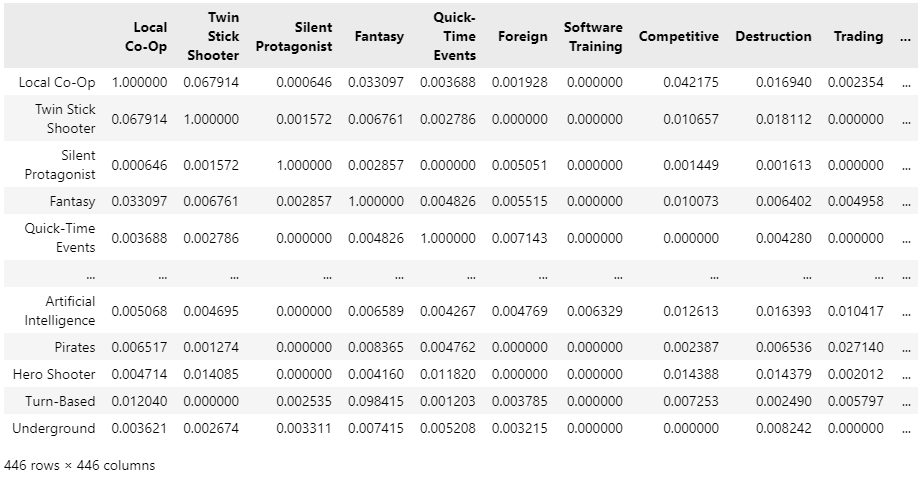
Let us make a manual check of the top 10 samples for some very common tags, to see if the result makes sense:

The result looks very promising! We started from plain categorical data (only convertible to 0 and 1), but we have extracted the semantic relationship between tags (without even using a neural network).

b. Use a pre-trained neural network

Equally, we can extract existing relationships between our samples using a pre-trained encoder. This solution, however, ignores the relationships that can only be extracted from our data, only focusing on existing semantic relationships of the human language. This may not be a well-suited solution to work on top of retail-based data.

On the other hand, by using a neural network we would not need to build a relationship matrix: hence, this is a proper solution for scalability. For example, if we had to analyze a large batch of Twitter data, we reach 53.300 tags. Computing a co-occurrence matrix from this number of tags will result in a sparse matrix of size 2,500,000,000 (quite a non-practical feat). Instead, by using a standard encoder that outputs a vector length of 384, the resulting matrix will have a total size of 19,200,200.

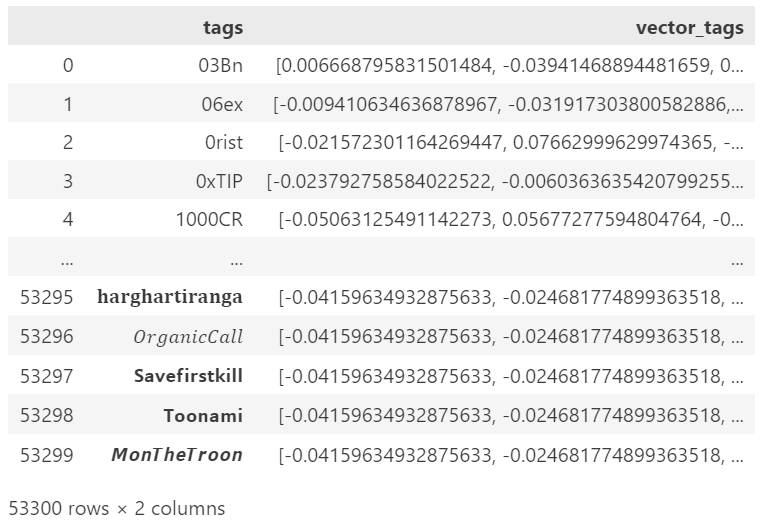
2. Encoding queries and samples

Our goal is to build a search engine capable of supporting the semantic tag search: with the format we have been building, the only technology capable of supporting such an enterprise is vector search. Hence, we need to find a proper encoding algorithm to convert both our samples and queries into vectors.

In most encoding algorithms, we encode both queries and samples using the same algorithm. However, each sample contains more than one tag, each represented by a different set of relationships that we need to capture in a single vector.

In addition, we need to address the aforementioned problem of scalability, and we will do so by using a PCA module (when we use a co-occurrence matrix, instead, we can skip the PCA because there is no need to compress our vectors).

When the number of tags becomes too large, we need to abandon the possibility of computing a co-occurrence matrix, because it scales at a squared rate. Therefore, we can extract the vector of each existing tag using a pre-trained neural network (the first step in the PCA module). For example, all-MiniLM-L6-v2 converts each tag into a vector of length 384.

We can then transpose the obtained matrix, and compress it: we will initially encode our queries/samples using 1 and 0 for the available tag indexes, resulting in an initial vector of the same length as our initial matrix (53,300). At this point, we can use our pre-computed PCA instance to compress the same sparse vector in 384 dims.

Encoding samples

In the case of our samples, the process ends just right after the PCA compression (when activated).

Encoding queries: Covariate Encoding

Our query, however, needs to be encoded differently: we need to take into account the relationships associated with each existing tag. This process is executed by first summing our compressed vector to the compressed matrix (the total of all existing relationships). Now that we have obtained a matrix (384×384), we will need to average it, obtaining our query vector.

Because we will make use of Euclidean search, it will first prioritize the search for features with the highest score (ideally, the one we activated using the number 1), but it will also consider the additional minor scores.

Weighted search

Because we are averaging vectors together, we can even apply a weight to this calculation, and the vectors will be impacted differently from the query tags.

3. Perform the semantic tag search using vector retrieval

The question you might be asking is: why did we undergo this complex encoding process, rather than just inputting the pair of tags into a function and obtaining a score — f(query, sample)?

If you are familiar with vector-based search engines, you will already know the answer. By performing calculations by pairs, in the case of just 40,000 samples the computing power required is huge (can take up to 10 seconds for a single query): it is not a scalable practice. However, if we choose to perform a vector retrieval of 40,000 samples, the search will finish in 0.1 seconds: it is a highly scalable practice, which in our case is perfect.

4. Validate

For an algorithm to be effective, needs to be validated. For now, we lack a proper mathematical validation (at first sight, averaging similarity scores from M already shows very promising results, but further research is needed for an objective metric backed up by proof).

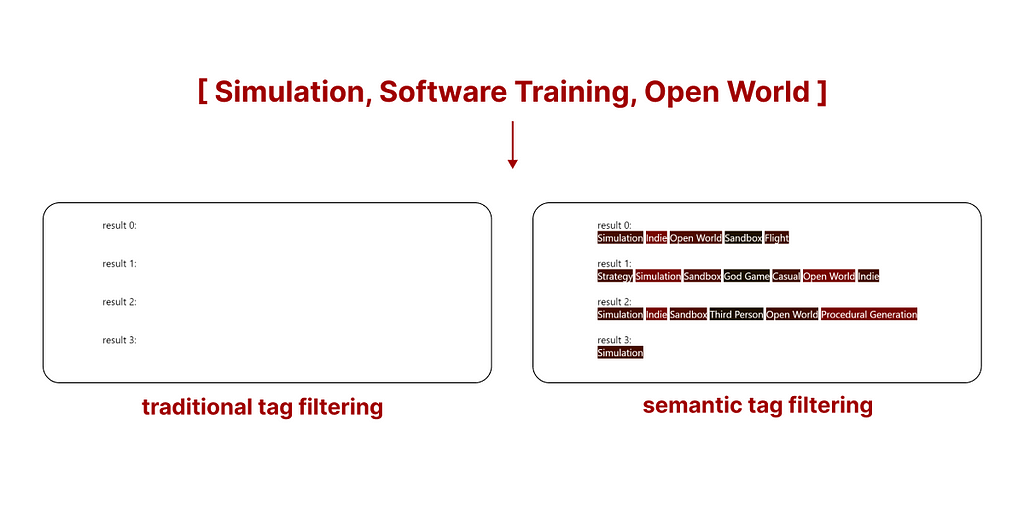
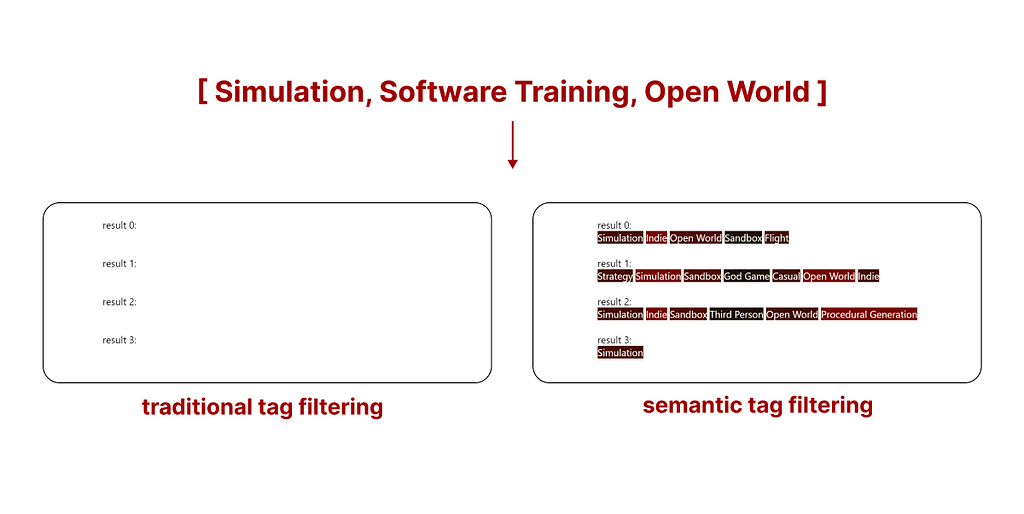
However, existing results are quite intuitive when visualized using a comparative example. The following is the top search result (what you are seeing are the tags assigned to this game) of both search methods.

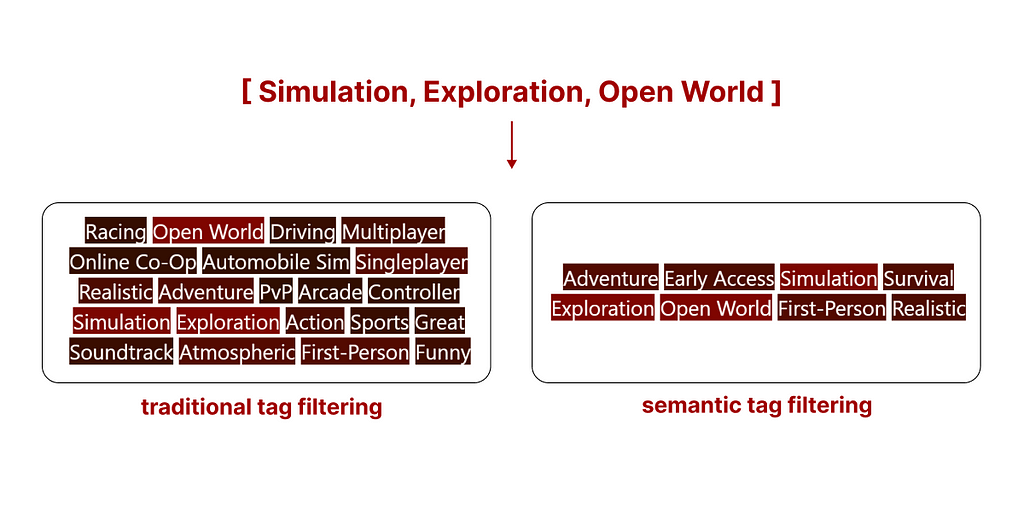
• Traditional tag search
  We can see how traditional search might (without additional rules, samples are filtered based on the availability of all tags, and not sorted) return a sample with a higher number of tags, but many of them may not be relevant.
• Semantic tag search
  Semantic tag search sorts all samples based on the relevance of all tags, in simple terms, it disqualifies samples containing irrelevant tags.

The real advantage of this new system is that when traditional search does not return enough samples, we can select as many as we want using semantic tag search.

In the example above, using traditional tag filtering does not return any game from the Steam library. However, by using semantic tag filtering we still get results that are not perfect, but the best ones matching our query. The ones you are seeing are the tags of the top 5 games matching our search.

Conclusion

Before now, it was not possible to filter tags also taking into account their semantic relationships without resorting to complex methods, such as clustering, deep learning, or multiple knn searches.

The degree of flexibility offered by this algorithm should allow the detachment from traditional manual labeling methods, which force the user to choose between a pre-defined set of tags, and open the possibility of using LLMs of VLMs to freely assign tags to a text or an image without being confined to a pre-existing structure, opening up new options for scalable and improved search methods.

It is with my best wishes that I open this algorithm to the world, and I hope it will be utilized to its full potential.

Introducing Semantic Tag Filtering: Enhancing Retrieval with Tag Similarity was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.