Squashing the Average: A Dive into Penalized Quantile Regression for Python

How to build penalized quantile regression models (with code!)

This is my third post on the series about penalized regression. In the first one we talked about how to implement a sparse group lasso in python, one of the best variable selection alternatives available nowadays for regression models, and in the second we talked about adaptive estimators, and how they are much better than their traditional counterparts. But today I would like to talk about quantile regression. and delve into the realm of high-dimensional quantile regression using the robust asgl package, focusing on the implementation of quantile regression with an adaptive lasso penalization.

Today we will see:

• What is quantile regression
• What are the advantages of quantile regression compared to traditional least squares regression
• How to implement penalized quantile regression models in python

What is quantile regression

Let’s kick things off with something many of us have probably encountered: least squares regression. This is the classic go-to method when we’re looking to predict an outcome based on some input variables. It works by finding the line (or hyperplane in higher dimensions) that best fits the data by minimizing the squared differences between observed and predicted values. In simpler terms, it’s like trying to draw the smoothest line through a scatterplot of data points. But here’s the catch: it’s all about the mean. Least squares regression focuses solely on modeling the average trend in the data.

So, what’s the issue with just modeling the mean? Well, life isn’t always about averages. Imagine you’re analyzing income data, which is often skewed by a few high earners. Or consider data with outliers, like real estate prices in a neighborhood with a sudden luxury condo development. In these situations, concentrating on the mean can give a skewed view, potentially leading to misleading insights.

Advantages of quantile regression

Enter quantile regression. Unlike its least squares sibling, quantile regression allows us to explore various quantiles (or percentiles) of the data distribution. This means we can understand how different parts of the data behave, beyond just the average. Want to know how the bottom 10% or the top 90% of your data are reacting to changes in input variables? Quantile regression has got you covered. It’s especially useful when dealing with data that has outliers or is heavily skewed, as it provides a more nuanced picture by looking at the distribution as a whole. They say one image is worth a thousand words, so let’s see how quantile regression and least squares regression look like in a couple of simple examples.

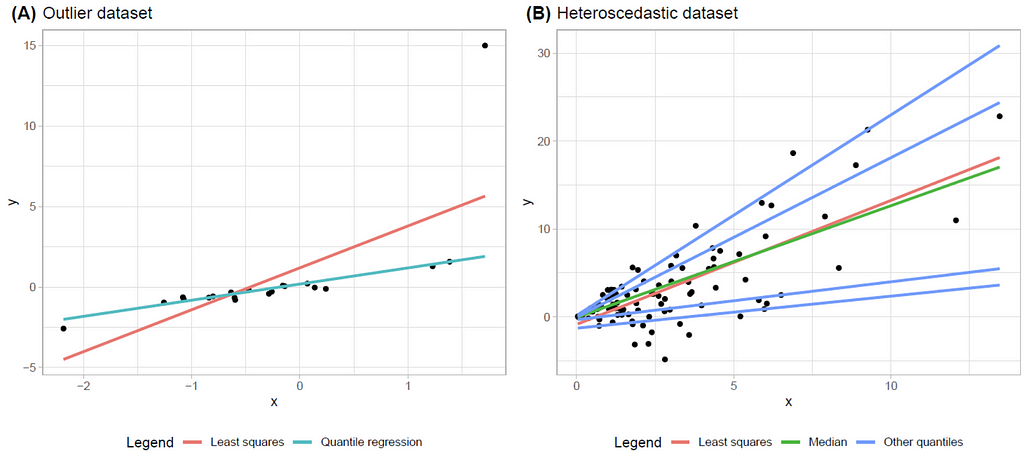
These two images show very simple regression models with one predictive variable and one response variable. The left image has an outlier on the top right corner (that lonely dot over there). This outlier affects the estimation provided by least squares (the red line), which is way out of way providing very poor predictions. But quantile regression is not affected by outliers, and it’s predictions are spot-on. On the right image we have a dataset that is heteroscedastic. What does that mean? Picture your data forming a cone shape, widening as the value of X increases. More technically, the variability of our response variable isn’t playing by the rules — it expands as X grows. Here, the least squares (red) and quantile regression for the median (green) trace similar paths, but they only tell part of the story. By introducing additional quantiles into the mix(in blue, 10%, 25%, 75% and 90%) we are able to capture how our data dances across the spectrum and see its behavior.

Implementations of quantile regression

High-dimensional scenarios, where the number of predictors exceeds the number of observations, are increasingly common in today’s data-driven world, popping up in fields like genomics, where thousands of genes might predict a single outcome, or in image processing, where countless pixels contribute to a single classification task. These complex situations demand the use of penalized regression models to manage the multitude of variables effectively. However, most existing software in R and Python offers limited options for penalizing quantile regression in such high-dimensional contexts.

This is where my Python package, asgl, appears. asgl package provides a comprehensive framework for fitting various penalized regression models, including sparse group lasso and adaptive lasso — techniques I’ve previously talked about in other posts. It is built on cutting-edge research and offers full compatibility with scikit-learn, allowing seamless integration with other machine learning tools.

Example (with code!)

Let’s see how we can use asgl to perform quantile regression with an adaptive lasso penalization. First, ensure the asgl library is installed:

pip install asgl

Next, we’ll demonstrate the implementation using synthetic data:

import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from asgl import Regressor

# Generate synthetic data
X, y = make_regression(n_samples=100, n_features=200, n_informative=10, noise=0.1, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Define and train the quantile regression model with adaptive lasso
model = Regressor(model='qr', penalization='alasso', quantile=0.5)

# Fit the model
model.fit(X_train, y_train)

# Make predictions
predictions = model.predict(X_test)

# Evaluate the model
mae = mean_absolute_error(y_test, predictions)
print(f'Mean Absolute Error: {mse:.3f}')

In this example, we generate a dataset with 100 samples and 200 features, where only 10 features are truly informative making it a high dimensional regression problem). The Regressor class from the asgl package is configured to perform quantile regression (by selecting model=’qr’) for the median (by selecting quantile=0.5). If we are interested in other quantiles, we just need to set the new quantile value somewhere in the (0, 1) interval. We solve an adaptive lasso penalization (by selecting penalization=’alasso’), and we could optimize other aspects of the model like how the adaptive weights are estimated etc, or use the default configuration.

Advantages of asgl

Let me finish by summarising the benefits of asgl:

1. Scalability: The package efficiently handles high-dimensional datasets, making it suitable for applications in a wide range of scenarios.
2. Flexibility: With support for various models and penalizations, asgl caters to diverse analytical needs.
3. Integration: Compatibility with scikit-learn simplifies model evaluation and hyperparameter tuning

And that’s it on this post about quantile regression! By squashing the average and exploring the full distribution of the data, we open up new possibilities for data-driven decision-making. Stay tuned for more insights into the world of penalized regression and the asgl library.

Squashing the Average: A Dive into Penalized Quantile Regression for Python was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.