Reinforcement Learning, Part 6: n-step Bootstrapping

Pushing the boundaries: generalizing temporal difference algorithms

Introduction

Reinforcement learning is a domain in machine learning that introduces the concept of an agent learning optimal strategies in complex environments. The agent learns from its actions, which result in rewards, based on the environment’s state. Reinforcement learning is a challenging topic and differs significantly from other areas of machine learning.

What is remarkable about reinforcement learning is that the same algorithms can be used to enable the agent adapt to completely different, unknown, and complex conditions.

Note. To fully understand the concepts included in this article, it is highly recommended to be familiar with the basics of Monte Carlo methods and temporal difference learning introduced in the previous articles.

• Reinforcement Learning, Part 3: Monte Carlo Methods
• Reinforcement Learning, Part 5: Temporal-Difference Learning

About this article

In the previous part, we analyzed how TD algorithms work by combining principles of dynamic programming and MC methods. In addition, we looked at a one-step TD algorithm — the simplest TD implementation. In this article, we will generalize TD concepts and see when it may be advantageous to use other algorithm variants.

This article is based on Chapter 7 of the book “Reinforcement Learning” written by Richard S. Sutton and Andrew G. Barto. I highly appreciate the efforts of the authors who contributed to the publication of this book.

Idea

Let us pause for a second and understand what one-step TD and MC algorithms have in common. If we omit overly specific details, we will notice that both of them are actually very similar and use the same state update rule except for a single difference:

• One-step TD updates every state by looking at the n = 1 next state.
• MC updates every state after analyzing the whole episode. This can be roughly perceived as an update for every state occurring after n steps (where n can be potentially a large number).

We have two extreme cases where n = 1 and where n = the number of remaining states in the episode sequence. A logical question arises: could we use a value of n that falls somewhere in the middle of these extreme values?

The answer is yes. And this concept is generalized through n-step Bootstrapping.

Workflow

In one-step TD, we analyze the difference between the received reward and how the state value changes by switching from the current state to the next (n = 1). This idea can be easily generalized to multiple steps. To do this, let us introduce the n-step return, which calculates the accumulated discounted reward between the current state t and the future state at step t + n. In addition, it also adds state value at step t + n.

Using the analogous update rule introduced in previous articles, this time we can compare an n-step return with the current state value and derive a new update rule:

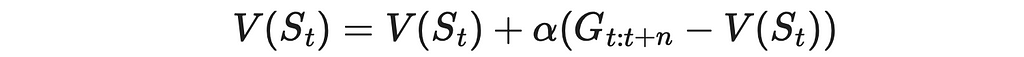
To better understand the workflow, let us draw a diagram of state relationships for several values of n. The diagram below demonstrates how information about next states and rewards is used to update previous states in the sequence.

For instance, let us take the case of 3-step TD:

• The beginning of the episode is generated up until the state S₃.
• State S₀ is updated by using the 3-step return, which sums up rewards R₁, R₂ and R₃ and the value of state S₃.
• State S₄ is generated.
• State S₁ is updated by using the 3-step return, which sums up rewards R₂, R₃ and R₄ and the value of state S₄.
• State S₅ is generated.
• State S₅ is updated by using the 3-step return, which sums up rewards R₃, R₄ and R₅ and the value of state S₅.
• The analogous process is repeated until we reach the last state of the episode.

If for a given state, there are fewer than n states left to calculate the n-step return, then the truncated n-step return is used instead, accumulating available rewards until the terminal state.

If n = ∞, then n-step TD is a Monte Carlo algorithm.

n-step TD control

In part 5, we discussed Sarsa, Q-learning and Expected Sarsa algorithms. All of them were based on using information from the next state. As we have already done in this article, we can expand this idea to n-step learning. To achieve this, the only change that needs to be made is to adjust their update formulas to use information not from the next state but from n steps later. Everything else will remain the same.

Choosing the best value of n

In part 5, we also highlighted the advantages of one-step TD algorithms over MC methods and how they lead to faster convergence. If so, why not always use one-step TD instead of n-step methods? As it turns out in practice, n = 1 is not always optimal value. Let us look at an example provided by Richard S. Sutton and Andrew G. Barto’s RL book. This example shows a situation where using larger values of n optimizes the learning process.

The image below shows a path made by the agent in a given maze during the first episode of the Sarsa algorithm. The agent’s goal is to find the shortest path to X. When the agent steps on X, it receives a reward R = 1. Every other step made in the maze results in a reward R = 0.

Let us now compare how the agent learns in 1-step Sarsa and 10-step Sarsa. We will assume that all action values are initialised to 0.

In 1-step Sarsa, for every move, the update is performed based only on the information from the next state. This means the only action value with a meaningful update is the one that leads directly to the goal X in a single step. In this case, the agent receives a positive reward and thus learns that making the “up” final move is indeed an optimal decision. However, all other updates do not make any impact because the received reward R = 0 does not change any action values.

On the other hand, in 10-step Sarsa, the final move will propagate its positive reward to the action values for the last 10 moves. In this way, the agent will learn much more information from the episode.

Therefore, in these maze settings, the larger values of n would make the agent learn faster.

Having looked at this example, we can conclude an important fact:

The best value of n in temporal difference learning is problem-dependent.

Conclusion

The generalization of one-step TD and Monte Carlo methods into n-step algorithms plays an important role in reinforcement learning as the best value of n usually lies between these two extremes.

Apart from this, there is no general rule for choosing the best value of n since every problem is unique. While larger values of n lead to more delayed updates, they can still perform better than smaller ones. Ideally one should treat n as a hyperparameter and carefully select it to find the optimum.

Resources

• Reinforcement Learning. An Introduction. Second Edition | Richard S. Sutton and Andrew G. Barto

All images unless otherwise noted are by the author.

Reinforcement Learning, Part 6: n-step Bootstrapping was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.